פנגייה

HTF1_008 הסעה טבעית

• זמן קריאה: 7 דק'

מבוא

הסעה טבעית היא מנגנון הסעה שמונע ע”י שינוי צפיפות בזורם המתחמם/מתקרר. זורם שנהיה פחות צפוף עולה בגלל כוחות ציפה ולהפך. כמובן שפעולה זו תלויה בכוח הכבידה.
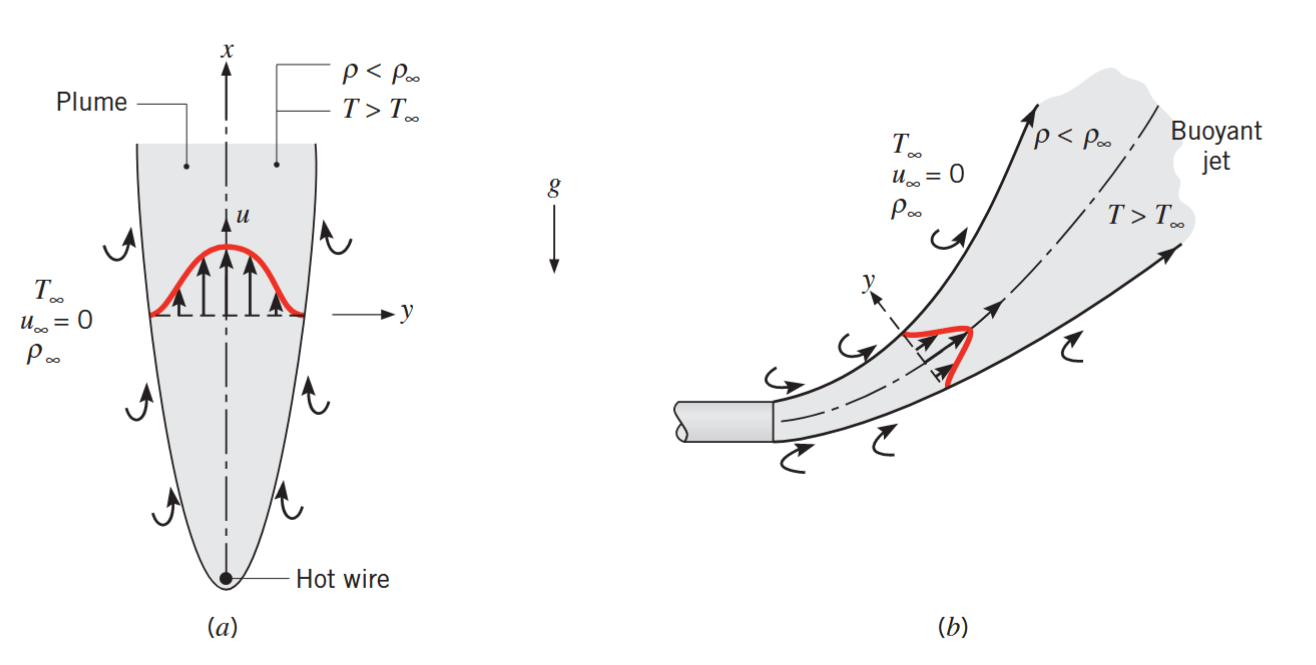
bookhue

שכבת גבול המתפתחת באופן טבעי - מכוח הציפה על הזורם. (a) שכבת גבול על חוט חם אנכי. (b) שכבת גבול מאגזוז אופקי. (Bergman & Lavine, 2017).

מאחר ומהירויות זרימה טבעית לרוב נמוכות יותר מהמהירויות בזרימה מאולצת, קצב מעבר החום בהסעה גם כן יותר נמוך. לפיכך זה מאוד מפתה להתעלם מתהליכי הסעה חופשית. אסור אסור אסור! בהמון מערכות שכוללות מעברי חום בתצורות שונות, הסעה חופשית היא הגורם הכי גדול להתנגדות מערכת חום, ולכן היא מאוד קריטית בניתוח והבנת הביצועים של המערכת. מעבר לכך, כאשר אנו רוצים להקטין את קצב מעבר החום, או אם אנו רוצים לחסוך בכסף, אנו נעדיף הסעה חופשית מאשר הסעה מאולצת.

משוואות שכבת הגבול בהסעה טבעית

במקרה של הסעה טבעית, משוואה (IH6.28) הופכת להיות פשוט:

בהסעה טבעית, , שהוא גרדיאנט הלחץ של הזרימה החופשית מחוץ לשכבת הגבול, לא זניח. אבל מחוץ לשכבת הגבול נשים לב ש- , ולכן יתייקם:

נציב זאת לתוך (IH9.1) ונקבל:

כאשר .

כדי לפתור את משוואה זו אנו משתמשים במה שנקרא קירוב בוסינסק (Boussinesq). נגדיר:

כאשר הסימון מתייחס לכך שאנו מחשבים את הנגזרת בלחץ קבוע.
תכונה תרמודינמית זו של הזורם היא מדד לשינוי הצפיפות כתוצאה משינוי בטמפרטורה, בלחץ קבוע. נוכל לקרב אותה ע”י הביטוי:

נסיק ש:

מהצבה בחזרה במשוואה (IH9.2):

מבחינת שאר משוואות השימור (מסה ואנרגיה), הן נשארות אותו הדבר:

במקרים מסוימים ניתן לחשב את ממשוות המצב. למשל, לגזים אידיאליים, . לכן, כאשר נציב זאת במשוואה (IH9.3) נקבל:

כאשר הוא הטמפרטורה ב-קלוין. לנוזלים וגזים לא אידיאליים, פורשים לטבלאות קיטור (נמצא ב- Appendix A בספר).

נרמול משוואות השימור בהסעה טבעית

לאחר נרמול, נקבל שמשוואות השימור:

מכיוון שאנחנו חופשיים לבחור איך שבא לנו, נבחר , כך שהמקדם של במשוואה (IH9.8) הוא פשוט . ממהירות אופיינית זו, אנו יודעים לבטא את ריינולדס כ:

נהוג להגדיר עוד מספר נחמד:

הגדרה:

מספר גרשהוף (Grashof) מוגדר כ:

כעת נוכל לרשום את (IH9.8) ו-(IH9.9) באופן הבא:

ניתן לראות שמספר גרשהוף משחק את אותו התפקיד של מספר ריינולדס בהסעה מאולצת. כלומר, בעוד מספר ריינולדס הוא מדד לכוחות האינרציאליים יחסית לכוחות הצמיגיים, מספר גרשהוף הוא מדד לכוחות הציפה ביחס לכוחות הצמיגיים. לכן, נצפה שלקורלציות מעברי חום להסעה טבעית יהיה את הצורה:

כוחות אינרציה וציפה תמיד קיימים בכל בעיית הסעה מאולצת (חוץ ממקרים של כבידה אפסית). בנוסף, כוחות ציפה ואינרציה קיימים גם בשכבת גבול באיור לעיל אם המהירות המציפה, , לא אפסית. כלומר, במקרה הכללי, שבו אנו לא יכולים להזניח לא את הציפה, ולא את האינרציה (), למספר נוסלט יהיה את הצורה:

אם כוחות הציפה זניחים יחסית לכוחות האינרציה (), אנו למעשה מקבלים הסעה מאולצת:

אם כוחות האינרציה זניחים ביחס לכוחות הציפה (), נקבל את משוואה (IH9.11).

ראו טבלה 9-4.

הסעה טבעית על פלטה שטוחה

בקורס אנו נתמקד בהסעה על פלטה שטוחה, כי זה מה שאנו יודעים לפתור.

הסעה טבעית למינרית

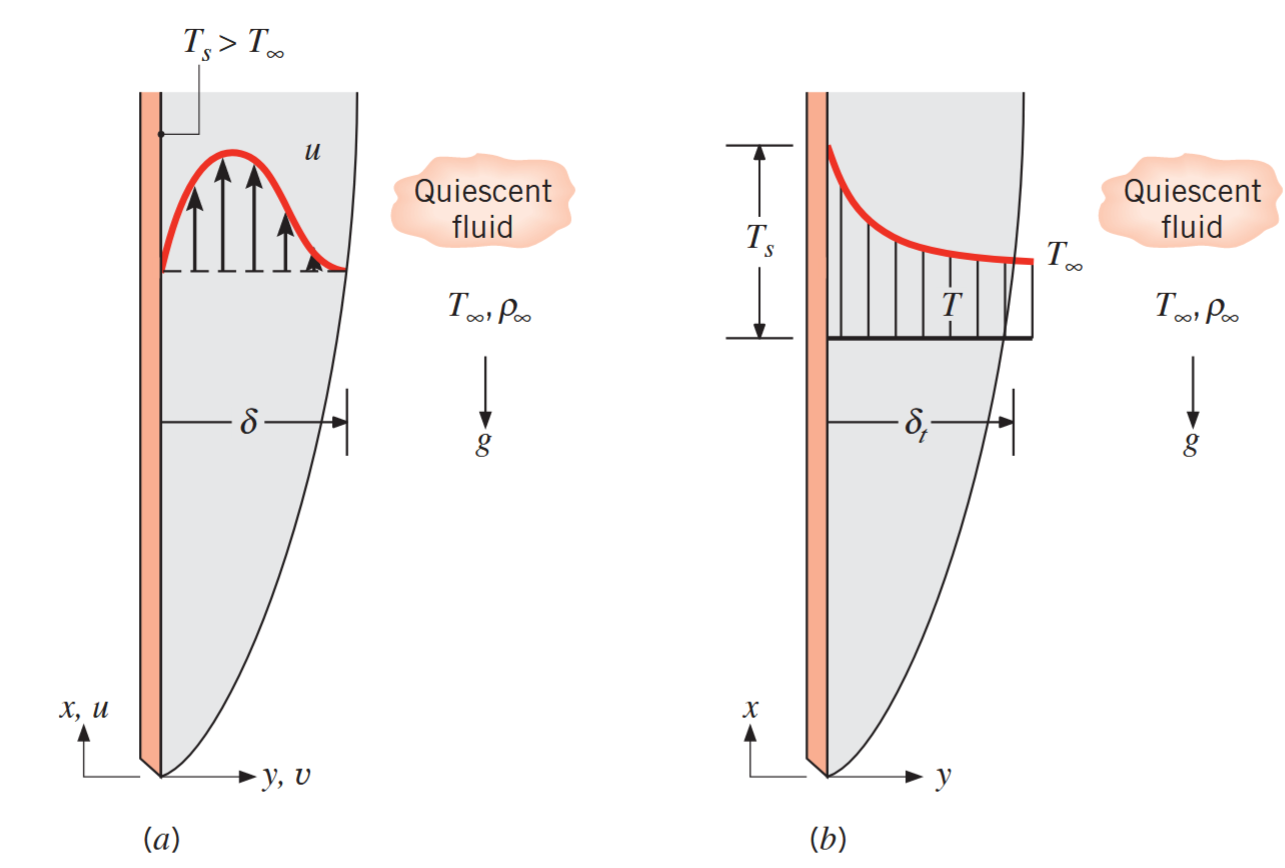
bookhue

התפתחות שכבת גבול על פלטה שטוחה אנכית. (a) שכבת גבול מהירות. (b) שכבת גבול תרמית. (Bergman & Lavine, 2017).

כדי לפתור את משוואות שכבת הגבול למקרה זה, מציעים מעבר קואורדינטות מהצורה:

מהצבה בשימור התנע והאנרגיה נוכל לחלץ את מספר נוסלט:

מה שמעיד על כך שגרדיאנט הטמפרטורה החסר ממדי בשפה הוא פונקציה של מספר פרנדטל . תלות זו מוצגת באיור הבא:
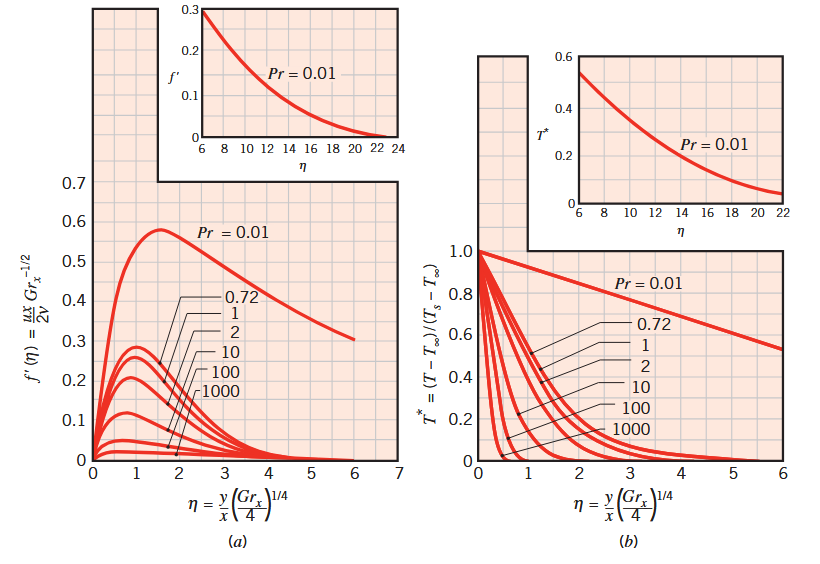
bookhue

שכבות גבול למינריות, בהסעה חופשית, על פלטה איזותרמית, אנכית. (a) פרופילי מהירות. (b) פרופילי טמפרטורה. (Bergman & Lavine, 2017).

מבחינה מספרית, ניתן לחשב את באופן הבא:

שתקף עבור .

בעזרת משוואה (IH9.19) נוכל למצוא את מקדם נוסלט הממוצע:

או, בעזרת משוואה (IH9.19), עם :

תוצאות אלו תקיפות בין אם או . אם , התנאים מתהפכים מהאיור הראשון.

הסעה טבעית טורבולנטית

כמו בהסעה מאולצת, בשלב מסוים אנו עוברים מזרימה למינרית לטורבולנטית.

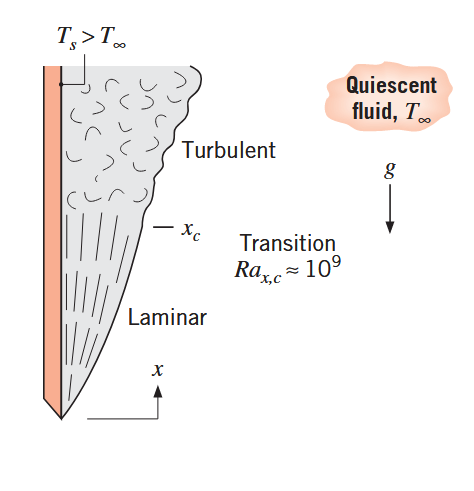
bookhue

שכבת גבול בהסעה טבעית במעבר לזרימה טורבולנטית על פלטה אנכית. (Bergman & Lavine, 2017).

מעבר לזרימה טורבולנטית בהסעה טבעית תלוי בגודל היחסי של כוחות הציפה והצמיגות בזורם. נהוג לקשר את התרחשותה במונחים של עוד מספר:

הגדרה: מספר ריילי

מספר ריילי (Rayleigh) מוגדר באופן הבא:

נניח בקורס שהמעבר לזרימה טורבולנטית בהסעה טבעית מתרחש כאשר:

כך שעלינו להשתמש בנוסחאות לעיל רק עבור .

קורלציות אמפיריות להסעה טבעית

רוב הקורלציות להסעה טבעית הן אמפיריות, והן מהצורה:

לרוב, לזרימות למינריות ו- לזרימות טורבולנטיות, בהתאמה.

הערה:

כל תכונות החומר מחושבות עבור הטמפרטורה הממוצעת .

פלטה אנכית

לפלטה אנכית, מציעים:

לזרימה למינרית ().
מציעים:

לזרימה טורבולנטית (). יש קורלציות יותר מרחיבות ומדויקות אבל למי יש כוח לכתוב אותן. הן מופיעות ב-(IH9.26) ו-(IH9.27) בספר.

פלטה אופקית

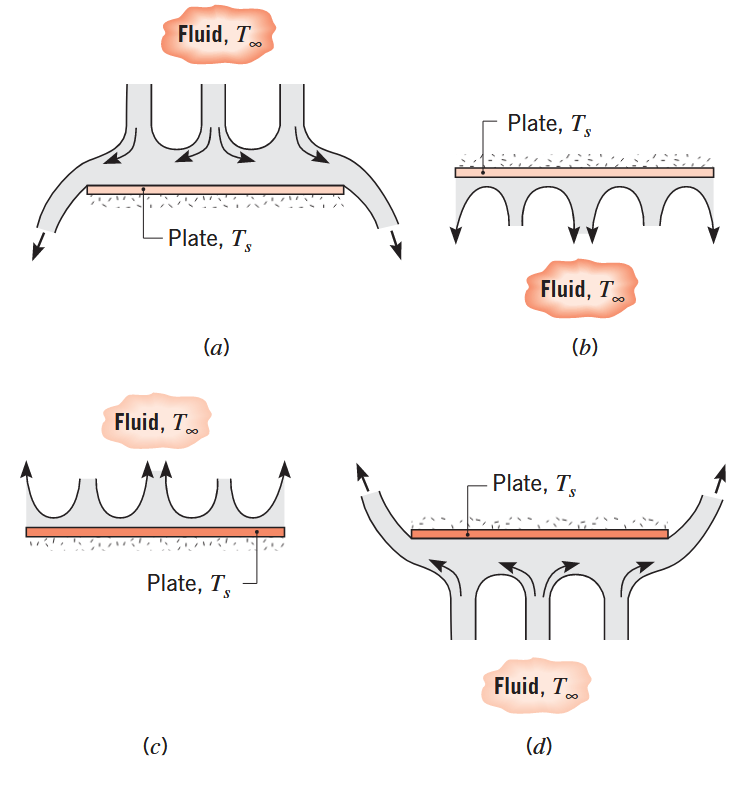
bookhue

הסעה טבעית על פלטה אופקית קרה () וחמה (). (a) משטח עליון של פלטה קרה. (b) משטח תחתון של פלטה קרה. (c) משטח עליון של פלטה חמה. (d) משטח תחתון של פלטה חמה. (Bergman & Lavine, 2017).

אם הפלטה אופקית, כוח הציפה פועל לחלוטין בנורמל למשטח. בין אם מדובר בפלטה קרה הפנויה כלפי מעלה או פלטה חמה הפנויה כלפי מטה, הנטייה של הזורם לרדת או לעלות, בהתאמה, נחסמת ע”י הפלטה עצמה. הזרימה חייבת לנוע אופקית לפני שהיא יכולה לרדת או לעלות מקצוות הפלטה, ואז ההסעה די לא משמעותית. לעומת זאת, לפלטה קרה הפונה כלפי מטה או פלטה חמה הפונה כלפי מעלה, הזרימה מונעת בעיקר מהתנועה ה-אנכית של הזורם.

לפלטות אופקיות בצורות שונות (ריבועים, מלבנים, עיגולים) עולה הצורך להגדיר אורך אופייני לשימוש במספרי ריינולדס ונוסלט. ניסויים הראו שניתן להשתמש בהגדרת אורך אופייני מסוים שעובדת עבור מספר רב של קורלציות:

כאשר ו- הם שטחי הפנים וההיקף של הפלטה, בהתאמה. בעזרת אורך אופייני זה, הקורלציות המומלצות למספר נוסלט הממוצע הן:

עבור המשטח העליון של פלטה חמה או המשטח התחתון של פלטה קרה:

עבור המשטח התחתון של פלטה חמה או המשטח העליון של פלטה קרה:

עמודים המציינים את העמוד הזה