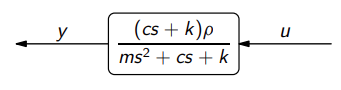ICT1_003 בקרה בחוג פתוח

→ קודם: ICT1_002הבא: ICT1_004 ←

מבוא

מערכת בקרה מוגדרת כהחִבְרוּר (interconnection) של מרכיבים שונים כדי ליצור מערכת שתניב תגובה רצויה כלשהי. מכיוון שתגובה זו ידועה (אנו יודעים איזה תגובה אנו רוצים שתהיה למערכת) ובעולם האמיתי המערכת לא תצליח לפלוט בדיוק את התגובה הרצויה, אנו מגדירים אות שגיאה בין האות הרצוי לאות האמיתי. השימוש באות שגיאה זה לרוב מוכנס בחזרה למערכת, מה שיוצר רצף פעולות בחוג סגור הנקראת מערכת משוב.

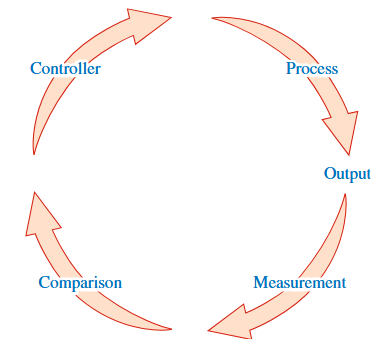
מערכת בחוג סגור. (Dorf & Bishop, 2022).

זהו למעשה המקרה של מערכות בטבע כמו מערכות ביולוגיות או פיזיולוגיות. למשל, הדופק בגוף האדם הוא דוגמה למערכת משוב השומרת על דופק רצוי מסוים.

מערכת בחוּג פָּתוּחַ, או מערכת ללא משוב, מתוארת באיור הבא:

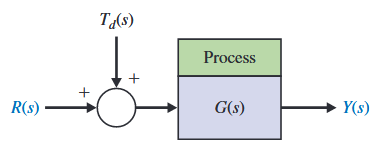
דיאגרמת בלוקים של מערכת בחוג פתוח עם אות הפרעה . (Dorf & Bishop, 2022).

האות הפרעה, משפיע ישירות על הפלט, . ללא משוב, המערכת בקרה מאוד רגישה להפרעות, לשינויים ב-, והמידע שיש לנו על .
אם המערכת בחוג פתוח לא מניבה תגובה רצויה, נוכל להכניס בקר בטור, לפני התהליך , ונתכנן את הפונקציית תמסורת כך שהפונקציית תמסורת הכללית תיתן את התגובה הרצויה. לשיטת בקרה זו קוראים בַּקָּרָה בְּחוּג פָּתוּחַ.

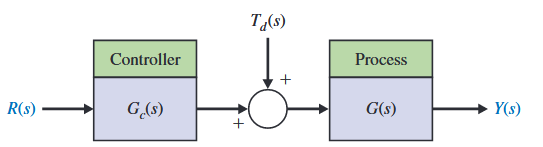
דיאגרמת בלוקים של מערכת בקרה בחוג פתוח (ללא משוב). (Dorf & Bishop, 2022).

הערה:

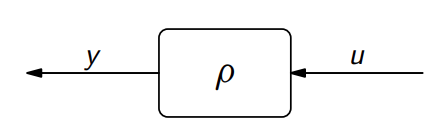
בדפי הרצאות של ליאוניד אנו משתמשים בסימון עבור (plant, process), ו- עבור (open-loop controller):

בסימונים אלו, גם:

• האות הוא הקלט.
• האות הוא הפלט (המבוקר).
• האות הוא הפלט הרצוי (reference trajectory).

המטרה שלנו היא למצוא כך ש- עבור אות נתון .

נתחיל מדוגמאות:

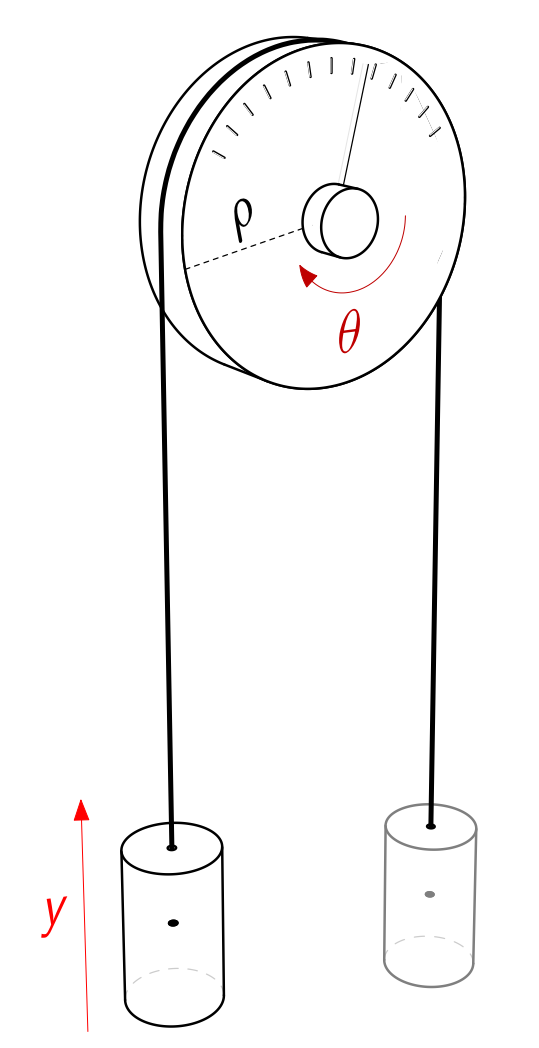
דוגמה: מערכת מסה-גלגלת פשוטה

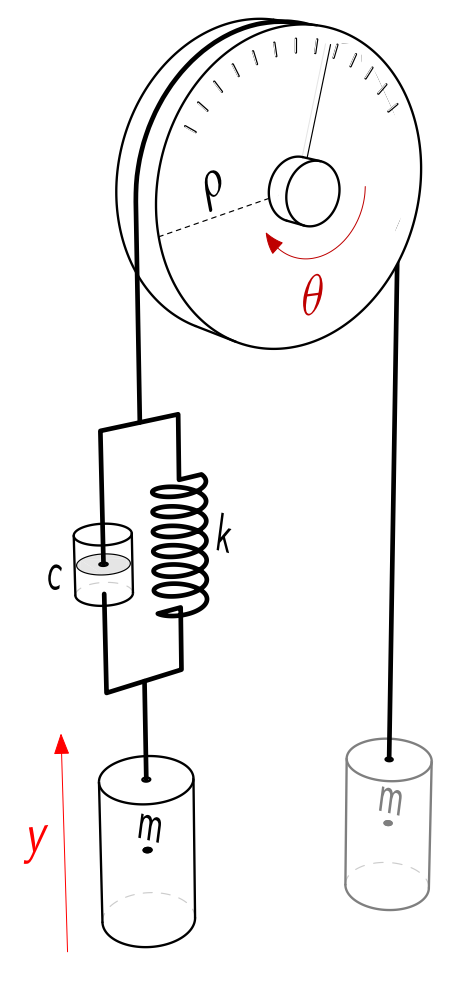
נביט בדוגמה הבאה של מערכת מסה-גלגלת:

מערכת מסה-גלגלת פשוטה, עם כקלט, ו- כפלט. (Leonid Mirkin’s Homepage, n.d.).

כיוון שהגלגלת ברדיוס , מספיק לנו להכפיל את הקלט ב- כדי לקבל את , ולכן המערכת מתוארת ע”י:

כדי למצוא כך ש- עבור נתון, נוכל פשוט לדרוש ש

כלומר:

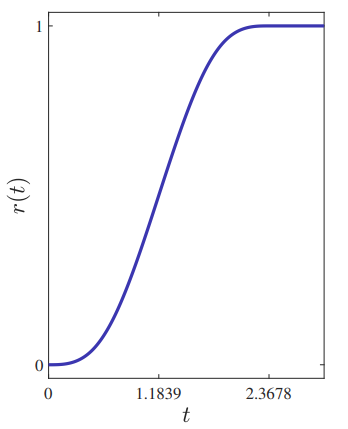
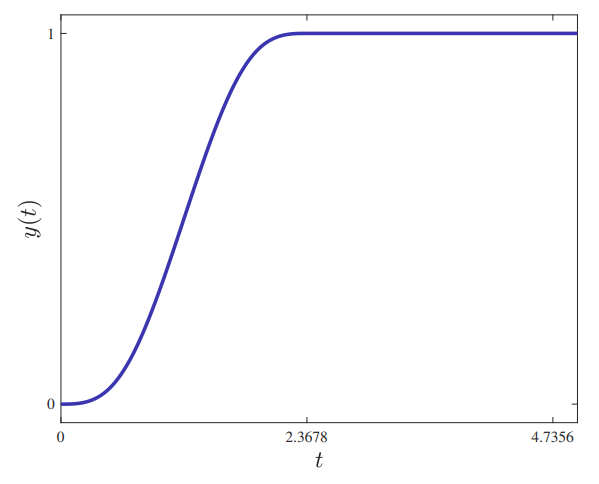
למשל, בהינתן ו- , והקלט הרצוי הוא:

נדרוש ש- , ונקבל שקיבלנו את הרצוי (כלומר, זהה ל-):

במקרה של מערכת יותר מסובכת, יהיה לנו טיפה יותר קשה “לנחש” את . למשל, במערכת מסה-גלגלת הבאה:

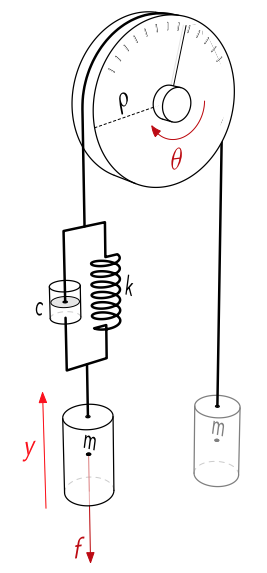
דוגמה: מערכת מסה-גלגלת עם ריסון וקפיץ

מערכת מסה-גלגלת עם ריסון וקפיץ, עם כקלט, ו- כפלט. (Leonid Mirkin’s Homepage, n.d.).

נוכל לתאר את מערכת זו ע”י:

לכן, כדי למצוא כך ש- , נדרוש:

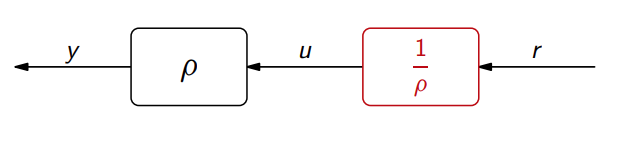
בקרים מהסוגים שרואים בדוגמאות לעיל פועלים לפי אותו עיקרון:

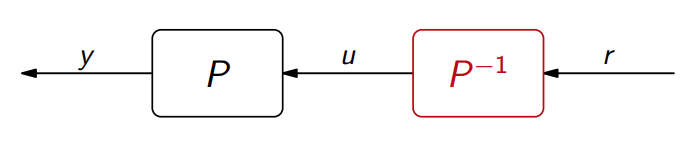
כלומר, הבקר:

לשיטה זו קוראים היפוך תהליך, ולמרות שהיא נדמית פשוטה, היא מאוד מוגבלת ביישומים שלה. בכל זאת, היא מהווה בסיס לרוב שיטות הבקרה.

מגבלות ההיפוך תהליך

אי ודאות במודל

נזכור כי המודלים שלנו על תהליכים מציאותיים אף פעם לא מושלמים. לכן, ה- ב- הוא לא התהליך האמיתי, אלא שיעור שלו, והמערכת בקרה האמיתית שבנינו היא בכלל:

עבור תהליך “אמיתי” כלשהו. כעת, מתקיים:

כך ש- כאשר , עם השגיאה:

דוגמה: מערכת מסה-גלגלת עם ריסון וקפיץ

במקרה של המערכת מסה-גלגלת עם ריסון וקפיץ טעינו במסה אנו נקבל:

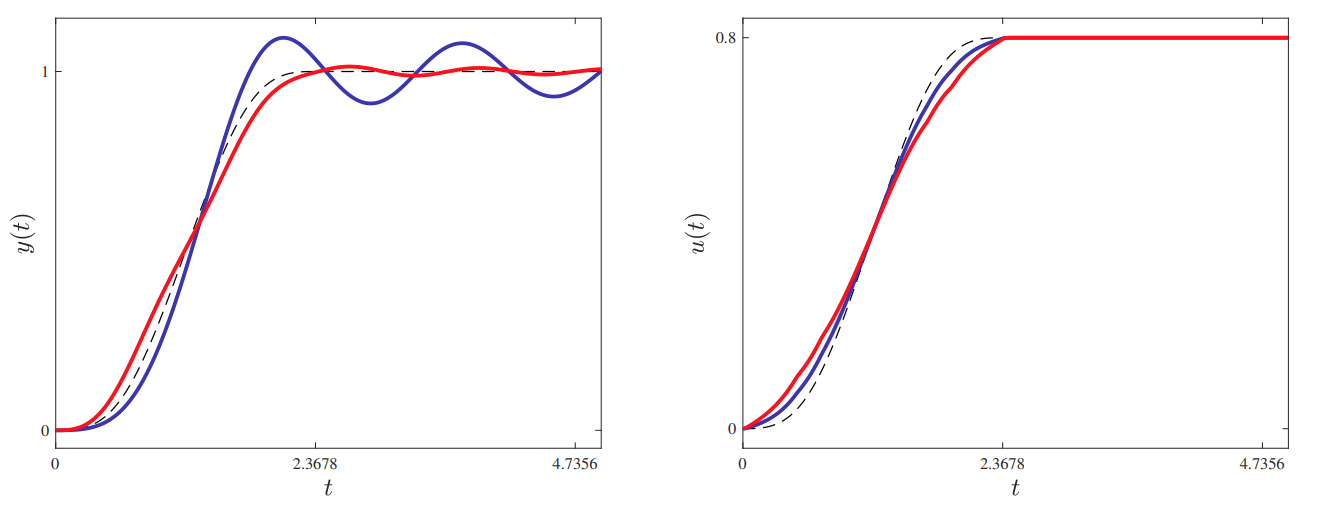
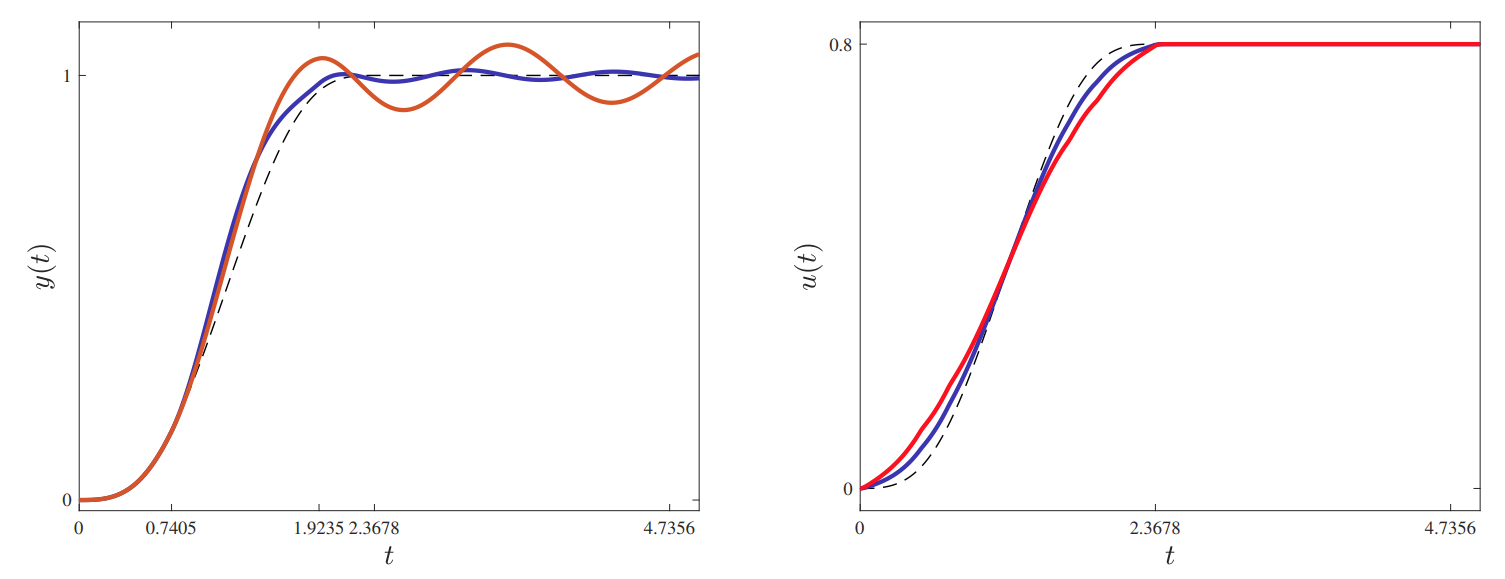
גרפים של הקלט מימין והפלט האמיתי משמאל. הקו המקווקו הוא הקלט/הפלט הדרוש. הגרף הכחול מתאר מערכת בקרה שהוזן לה , בעוד המסה האמיתית היא . הגרף האדום מתאר מערכת בקרה שהוזן לה , בעוד המסה האמיתית היא . הנתונים האחרים של המערכת הם . (Leonid Mirkin’s Homepage, n.d.).

ניתן גם לעשות ניסוי מחשבתי על המערכת הזו: במידה ואנו רוצים להעלות את המסה באופן שמתואר בקו המקווקו באיור לעיל (עד לגובה ), נדמיין את עצמנו מסובבים את הגלגלת בסך הכל רדיאנים. כדי להתאים את עצמי לגרף הדרוש (מבחינת מהירות, תאוצה וכו’), אסובב את הגלגלת גם כמעט באותו האופן. אם התחשבתי נכון בקפיץ ובריסון (כך שאני צריך להתחשב נכון גם במסה), אצליח לקבל את העקומה הדרושה ממני. אבל, אם למשל הנחתי שהמסה הרבה יותר קלה מהמציאות, אני עלול לסובב את הגלגלת לאט מדי בהתחלה ומהר מדי בסוף, מה שיוביל לתנודות גדולות של המסה - לא כנדרש בגרף של . טעות כזו מתוארת ע”י הגרף הכחול לעיל. הסיבה שהגרף הכחול תנודתי יותר מהגרף האדום הוא די מקרי וספציפי למערכת זו; יש הסבר לתופעה זו בהרצאה מספר 4 (הבאה בסדרה).

הפרעות

דרכים אחרות בהם הבקר היפוך עלול להיכשל בהם הוא במקרה של הפרעות. נוכל למדל את הפרעות אלו כאות הפרעה המשפיע על המערכת:

במקרה זה:

ואז השגיאה שלנו היא:

דוגמה: מערכת מסה-גלגלת עם ריסון וקפיץ

נביט בהשפעה של כוח חיצוני למערכת מסה-גלגלת עם ריסון וקפיץ.

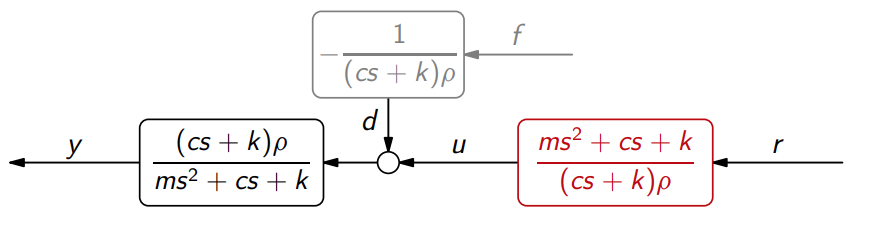
נוכל פשוט להוסיף את לדיאגרמה באופן הבא:

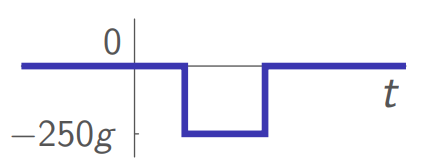
במידה ו-

𝟙𝟙

שהוא בעצם הפונקציה:

התגובות יהיו:

גרפים של הקלט מימין והפלט האמיתי משמאל. הקו המקווקו הוא הקלט/הפלט הדרוש. הגרף הכחול מתאר מערכת בה , בעוד הגרף האדום מתאר מערכת בה . הנתונים האחרים של המערכת הם .

יציבות פנימית

צמצום קטבים

הגדרה: צמצום

בהינתן חיבור בטור כמתואר בתרשים הבא:

אנו אומרים שישנו צמצום בטור אם סדר ההעתקה קטן יותר מסכום הסדרים של חלקיו, ו-.

פשר המשמעות של צמצום הוא שחלק מהדינמיקה של החלקים פשוט נעלמת מההעתקה . אם הדינמיקה שנעלמת היא לא יציבה, כלומר הקטבים שלה ב- , אנו אומרים שהצמצום לא יציב. במקרים של SISO (single-input single-output), הקטבים של חלק אחד יכולים להתבטל רק ע”י האפסים של האחר, ולכן לרוב נשתמש במונח צמצום קטבים/אפסים.

דוגמה:

יהי:

לכן:

כלומר, הקוטב של ב- מצומצם ע”י האפס של . זהו צמצום לא יציב אם .

יציבות פנימית של מערכות מחובררות

נביט בבקר בחוג פתוח הבא:

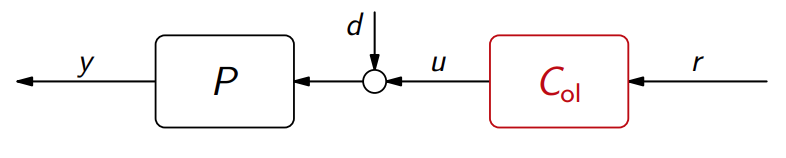
נוכל להציג את ההעתקה בין הקלט ו- לפלט ו- באופן מטריצי:

הגדרה: יציבות פנימית

נאמר שהבקר בחוג פתוח הוא יציב פנימית אם יציבים.
כיוון שהיציבות של ו- גוררת יציבות של , נסיק כי המערכת יציבה פנימית אמ”ם גם וגם הם יציבים.

נשים לב שאם ישנו צמצום לא יציב בין ו- אז הבקר לא יציב פנימית.

השלכות על בקר בחוג פתוח

ככלל, התנאים לאפשרות לבקרה באמצעות הפיכת תהליך הם אם התהליך :

1. יציב BIBO.
2. ללא אפסים ב-RHP ().
3. התהליך הוא strictly proper.

תרגילים

תרגיל 1

הביטו בתהליכים הבאים המבוקרים בחוג פתוח:

האם תהליכים אלו ניתנים לבקרה ע”י הבקר ?

פתרון:

1. התהליך הוא יציב (הוא proper וכל הקטבים שלו במישור השמאלי). הפונקציית תמסורת של הבקר היא: פונקציית תמסורת זו היא non-proper. במישור הזמן, הוא קובע כי: כלומר, הוא ניתן ליישום רק אם אנו יכולים למדוד את וגם את , וגם אם חסום.
2. התהליך יציב. הפונקציית תמסורת של הבקר: הבקר הוא proper אבל יש לו קוטב חיובי, כך שהוא לא יציב, והוא ידרוש קלט לא חסום - אין יציבות פנימית.
3. התהליך לא יציב. הפונקציית תמסורת של הבקר: בכלל המערכת אנו מצמצים את הקוטב של , שהוא קוטב לא יציב, מה שיכל לגרום להתבדרות במקרה של הפרעה קטנה - אין יציבות פנימית.

תרגיל 2

האיור הבא מתאר רכב במסה הנוסע במעלה מדרון עם זווית . הכוח המניע הנוצר ע”י המנוע הוא האות המבוקר, שמטרתו הוא לשמור על מהירות המכונית ברמה מסוימת. לכוח ההתנגדות שלושה חלקים: הכוח כתוצאה מהכבידה, ; כוח הגרר ; ו- הכוחות כתוצאה מחיכוך הגלגול. בהנחה והמהירות של המכונית תמיד חיובית, ההתנגדות לגלגול היא , כאשר מקדם ההתנגדות לגלגול הוא . כוח הגרר פרופורציונלי למהירות בריבוע, כלומר , כאשר הוא קבוע שתלוי בצפיפות האוויר, שטח הפנים הקדמי של המכונית, ומקדם גרר התלוי בצורה של המכונית.

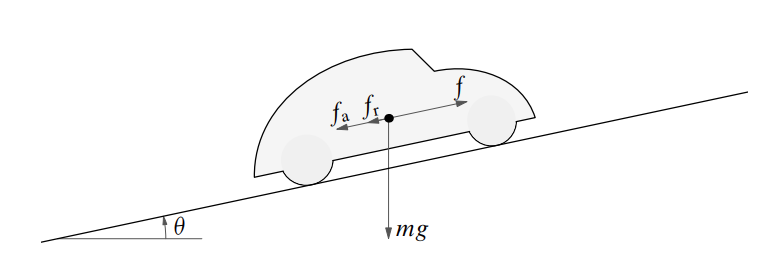
המערכת הנתונה על הרכב. (Leonid Mirkin’s Homepage, n.d.).

סעיף א’

מצאו את משוואות התנועה של המערכת ובצעו עליו לינאריזציה סביב נקודת שיווי המשקל:

סמנו את הקלט והפלט ע”י ו- בהתאמה.

פתרון:
מחוק שני של ניוטון:

זהו מד”ר מסדר ראשון, כך שנבחר את המצב של המערכת כ- . לכן, משוואת המצב היא:

נסמן את הצד הימני של המשוואה ב- . לכן:

נקודות שיווי המשקל צריכות לקיים . נקבל ש:

לכן, ישנו מיוחד עבור כל . נזכור שנתון לנו מסוים, אז נניח ואנו מתייחסים אליו מעכשיו.
נרצה לבצע לינאריזציה למערכת. הפרמטרים:

לכן משוואת המצב לאחר לינאריזציה:

כאשר:

הפונקציית תמסורת של המערכת היא:

זוהי מערכת מסדר ראשון, עם קבוע זמן שתלוי במהירות שיווי משקל. למעשה, כיוון ש- קטן כאשר גדל, המערכת מגיבה יותר מהר במהירויות גבוהות יותר.

סעיף ב’

יהי בקר מחוג פתוח בו הבקר יוצר אות מבוקר מאות מהירות . ציירו את הדיאגרמת בלוקים של מערכת זו. תכננו את ע”י היפוך תהליך. מתי בקר זה ניתן ליישום? חשבו את התגובה של המערכת הלינארית אם:

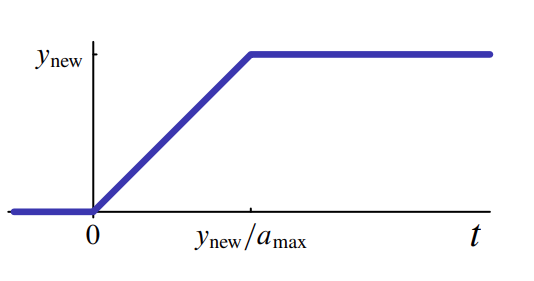
האות הנתון. (Leonid Mirkin’s Homepage, n.d.).

כאשר ו-.

פתרון:

מערכת בקר בחוג פתוח. (Leonid Mirkin’s Homepage, n.d.).

הפיכת תהליך:

נשים לב שזהו בקר non-proper. במידה ולא היינו יודעים מהו האות ייחוס , לא היינו יודעים להשתמש בבקר זה כי אני לא יודעים בהכרח את העתיד של אות זה (לא יודעים את ). אבל, במקרה זה נתון לנו, ולכן כן נוכל ליישם את בקר זה.

מאחר ו- :

כאשר נציב את הנתון, נקבל שהאות :

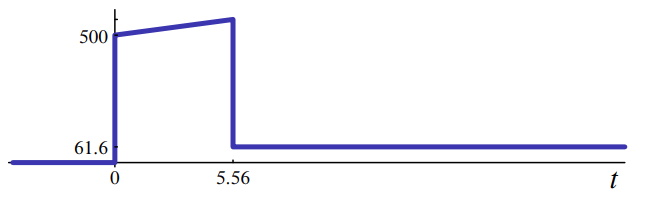
האות . (Leonid Mirkin’s Homepage, n.d.).

סעיף ג’

הניחו שלמדרון יש שיפוע טיפה שונה מהשיפוע שאיתו מידלנו את המערכת והבקר - נניח שהוא . רשמו את משוואת התנועה החדשה במקרה זה וחשבו את התגובה הלינארית ל- מסעיף קודם.

פתרון:
מבחינת משוואת התנועה של המערכת, לא הרבה השתנה חוץ מהחלפת ב-:

בנוסף, לא תלוי ב- ולכן הוא לא השתנה.
השיווי משקל כעת הוא:

אבל, לא שינינו את הכניסה . נשים לב שמהגדרת מתקיים , ולכן התגובה החדשה :

סיטואציה זו תואמת לדיאגרמה הבאה במקרה וה”הפרעה” היא:

בקר בחוג פתוח תחת אי-ודאות לגבי שיפוע המסלול. (Leonid Mirkin’s Homepage, n.d.).

השגיאה שלנו במצב מתמיד תהיה:

נוכל לראות את תגובת המכונית בגרף הבא בצבע אדום:

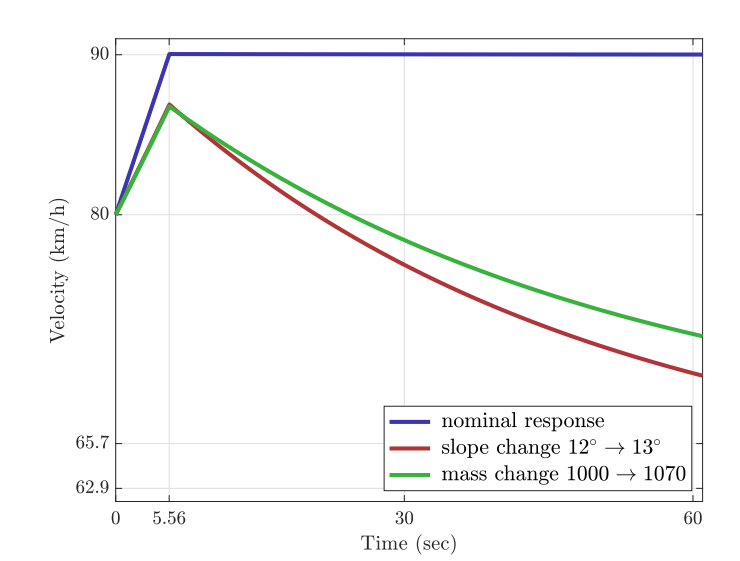
תגובות מהירות ל- הנתון. (Leonid Mirkin’s Homepage, n.d.).

סעיף ד’

הניחו כעת שהשיפוע הוא השיפוע הצפוי, אבל נוסע ששוקל נכנס לרכב, כך שמסת הרכב האמיתית הופכת להיות . מצאו את הדינמיקה החדשה של המערכת והתגובה הלינארית ל-.

פתרון:
כעת, השיווי משקל הוא:

ולכן:

סיטואציה זו תואמת לדיאגרמה הבאה במקרה וה”הפרעה” היא:

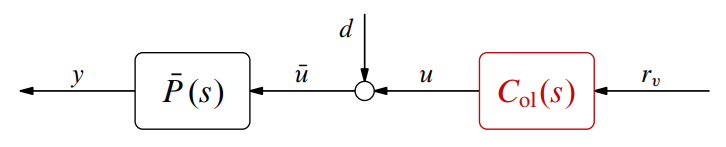
בקר בחוג פתוח תחת אי-ודאות לגבי מסת הרכב. (Leonid Mirkin’s Homepage, n.d.).

השגיאה שלנו במצב מתמיד תהיה:

תגובת המכונית מוצגת בגרף הקודם בצבע ירוק.

→ קודם: ICT1_002הבא: ICT1_004 ←