ICT1_EEQ Exam Example Questions

חלק א’

שאלה 1

דיאגרמת בלוקים.

נשים לב שבמקרה ו-, מתקיים:

ולכן:

נשים לב גם ש:

לכן לפי (1.1) ו-(1.2):

נקבל:

שאלה 2

נשים לב שבמקרה ו-:

ולכן:

נשים לב גם ש:

לכן לפי (1.3) ו-(1.4):

נקבל:

שאלה 3

לפי מנוע DC:

• הוא הזרם במנוע.
• הוא המומנט שמפעיל המנוע.
• הוא המהירות הזוויתית (של המנוע).
• הוא מתח ההחזר כא”מ.

שאלה 4

הקשר הוא:

כאשר הוא קבוע המנוע.

שאלה 5

הקשר הוא:

כאשר הוא קבוע כוח הכא”מ החוזר.

שאלה 6

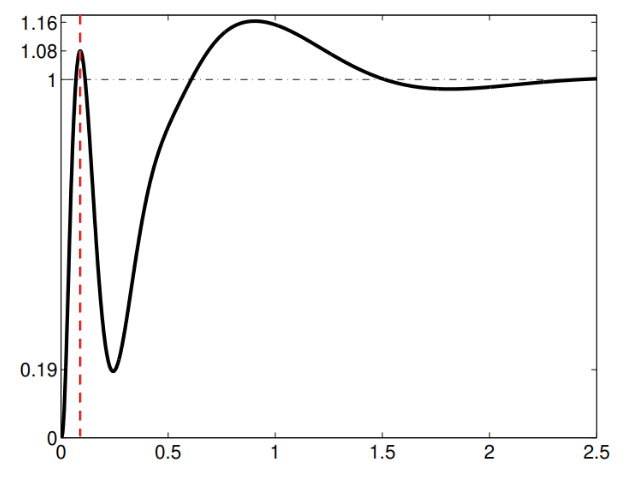
התגובה הנתונה.

נשים לב שבמצב מתמיד, . בנוסף, הערך המקסימלי הוא ולכן:

מבחינת התגובת-חסר, היא לא קיימת כי התגובה אף פעם לא יורדת מהערך ההתחלתי.

שאלה 7

ניתן לראות מהאיור שהתגובה מגיעה ל- (שזה ) בערך ב-:

שאלה 8

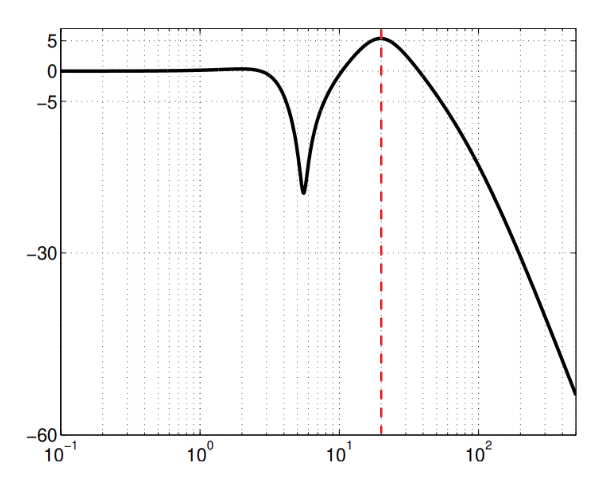
מהגרף ניתן להראות שהמקסימום ב-:

שאלה 9

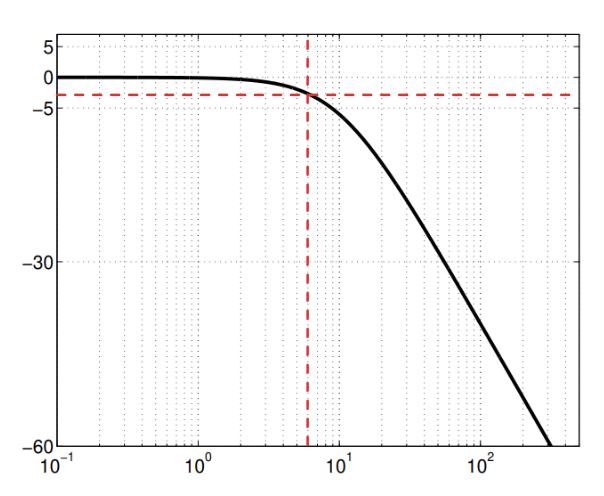
ניתן לראות שהפעם הראשונה בה ההגבר יורד מ- הוא ב-:

שאלה 10

• לפי ניתוח תגובת תדירות - ככל שהתהודה גדולה יותר מקבלים גדול יותר.
• כי יש לו את רוחב הפס הכי גדול, ולכן התגובה שלו תהיה הכי מהירה.
• כי יש לו את רוחב הפס הכי נמוך ולכן התגובה שלו הכי איטית.

שאלה 11

נשים לב שבמצב מתמיד, . בנוסף, הערך המקסימלי הוא ולכן:

שאלה 12

לפי ניתוח מערכות מסדר ראשון ושני, מאחר ול- יש קטבים מרוכבים, היא תת-מרוסנת, ולכן יש לה קטנה יותר מ-, שהיא מערכת מרוסנת-יתר כי הקטבים שלה ממשיים.

שאלה 13

לפי משפט הערך ההתחלתי, נסיק שעבור המערכות הנתונות (עם שני קטבים ואפס אחד), התגובת מדרגה () תהיה:

כלומר, מה שקובע את סימן השיפוע הוא הסימן של המקדם של במונה של . מאחר ורק מתחיל בשיפוע שלילי ורק ל- יש אפס חיובי, נסיק כי:

מה הקשר אפס חיובי? חשבתי המקדם של במונה צריך להיות שלילי?

נניח והמערכת היא מהצורה הכללית והמאוד לא סטנדרטית:

הערך במצב מתמיד הוא חיובי בכל הגרפים, ולכן לפי משפט הערך הסופי, היחס גם כן חיובי. מאחר ושני הקטבים שליליים (), זה אומר ש- חייב להיות חיובי, כלומר האפס חייב להיות חיובי.
מה שאני אומר פה בעצם זה שעבור תגובת מדרגה שחיובית במצב מתמיד של מערכות מהצורה הנתונה במפות, אם יש שיפוע התחלתי שלילי, יש אפס חיובי.

מאחר ול- יש קטבים ממשיים (מערכת מרוסנת-יתר) עם אפס שלילי אחד, לפי השפעה של קוטב נוסף ואפס נוסף, נקבל מערכת מרוסנת-יתר עם :

באותו אופן, השפעה של אפס נוסף למערכת עם שני קטבים מרוכבים (מערכת תת-מרוסנת) היא שנקבל מערכת תת-מרוסנת עם ו- יותר מוקצנים:

(ניתן גם להסביר את כך, כאשר פשוט עם הוספת אפס חיובי כך שנוצר ).

שאלה 14

לפי השפעה של קוטב נוסף, תגובת היתר תקטן.

שאלה 15

לפי השפעה של אפס נוסף, תגובת היתר תגדל (וגם תהיה תגובת-חסר).

שאלה 16

כאשר מוסיפים קוטב (שלילי), התגובה נהיית חלקה ואיטית יותר. כאשר מוסיפים אפס (שלילי), התגובה נהיית קיצונית יותר - זמן העלייה ירד. לכן, ל- זמן עלייה קצר יותר.

שאלה 17

לפי ההגדרה של רוחב-פס, נמצא עבור איזה מתקיים:

שאלה 18

אם ננסה לפתור באותו האופן נקבל משוואה מסדר רביעי עבור . במקום זאת, נשים לב ש:

לכן:

נסיק שאין למערכת רוחב-פס.

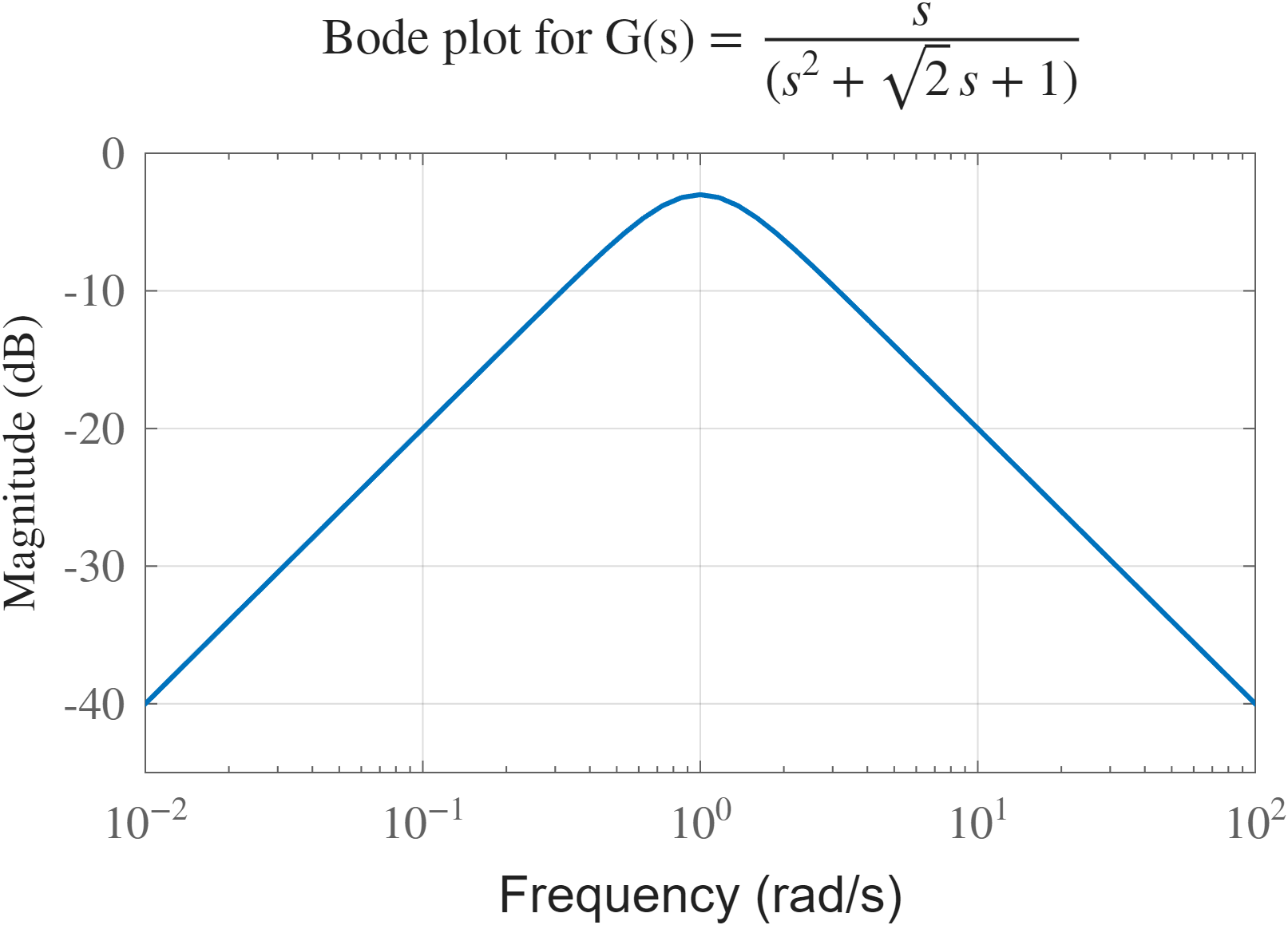
גרף בודה של המערכת הנתונה.

שאלה 19

ניתן לראות שאות היציאה כולל בתוכו (במצב המתמיד) אות בתדירות , שבמובנים של תדירות זוויתית זה . בנוסף, נשים לב שההגבר הסטטי של הכניסה לא עבר ליציאה, ולכן כנראה סינן את . נסיק שמדובר ב-א’, כי רק הוא מעביר את וגם לא מעביר את .

שאלה 20

אנו רוצים להנחית את כל התדרים מעל , אז נציע LPF מהצורה הפשוטה:

נציב את הדרישה:

נבחר ונקבל:

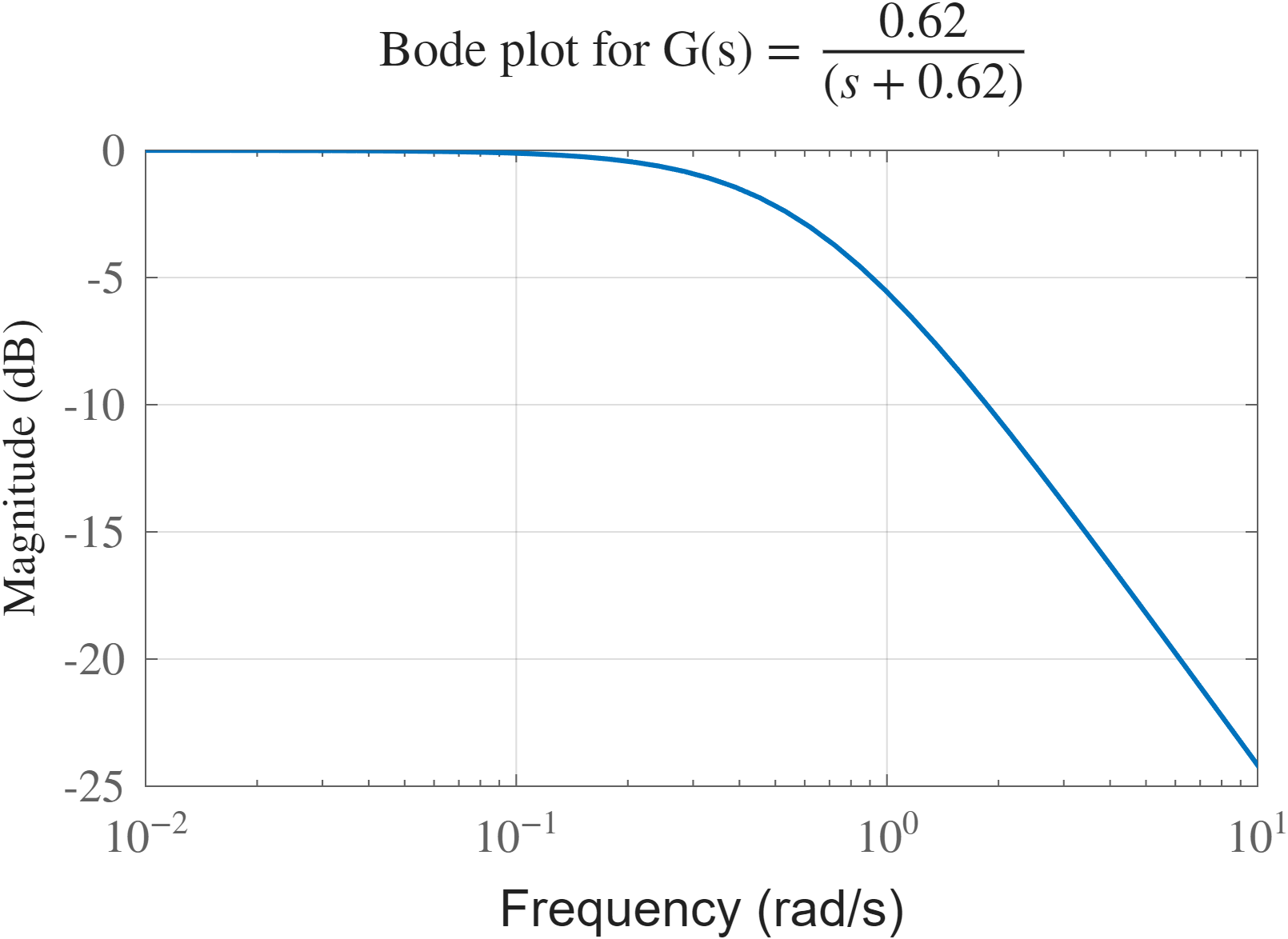
גרף בודה של המערכת המוצעת.

שאלה 21

באותו אופן כמו שאלה קודמת, ננחית את כל התדרים מעל ע”י LPF:

נציב את הדרישה:

(דרישה די מחמירה, אבל למי אכפת).

נבחר :

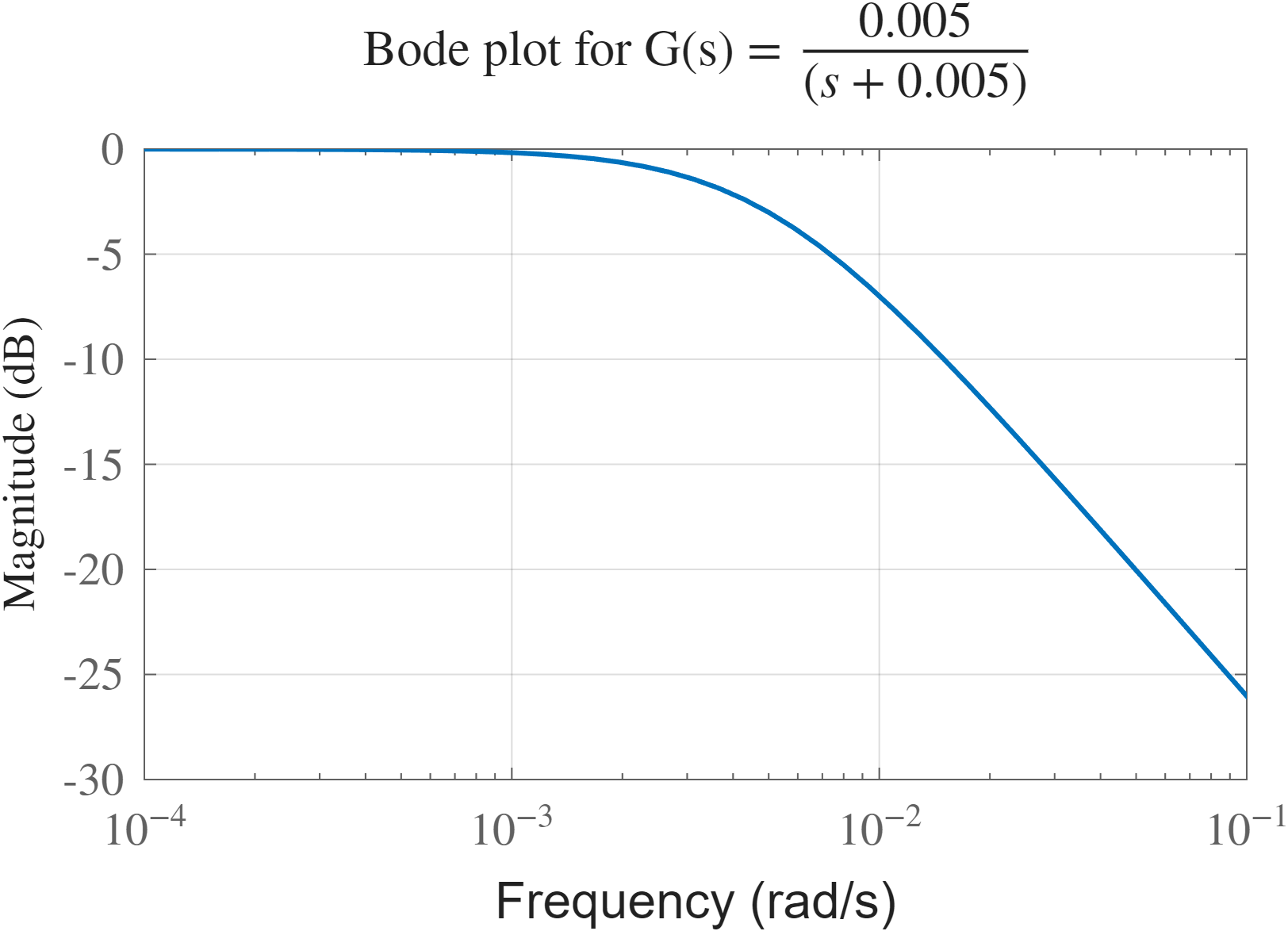
שאלה 22

ההבדל המרכזי ביניהם הוא שכל אחד מהם מגיע בזווית אחרת ל-. נשים לב ש:

נסיק כי:

שאלה 23

שוב, כל אחת אחד מהם מגיע בזווית אחרת ל-:

נסיק כי:

חלק ב’

שאלה 24

זהה לשאלה מתרגול.

שאלה 25

לפי מודל ייחוס, נרצה לבחור כך ש:

נשים לב של- יש עודף קוטב יחיד.

• עבור , הכל טוב ויפה כי יש לו גם עודף קוטב יחיד, ואין לו אפסים חיוביים.
• עבור , אנחנו בבעיה כי יש לו אפס חיובי, מה שאומר של- יהיה קוטב חיובי ואז הבקר לא יציב.
• עבור אנחנו גם בבעיה כי התהליך עצמו לא יציב. כל הפרעה תגרום להתבדרות המערכת.

שאלה 26

נשים לב ש- הוא proper וגם יש לנו שני קטבים ב-LHP הפתוח ולכן הוא יציב. נסיק שניתן לבקר את המערכת בעזרת מודל ייחוס עם לפחות עודף קוטב יחיד (כמו ל-), וכל עוד האפס (החיובי) של הוא גם אפס של , כדי לצמצם אותו.

שאלה 27

נשים לב של- אין קטבים יציבים, ולכן לא ניתן ליישם היפוך תהליך.

שאלה 28

נשים לב ש:

בנוסף, ההתמרת לפלס של ריצה היא ולכן:

נסיק כי:

ולכן:

(בסדר עברתי על כמה חוקי חדו”א של גבולות אבל אני לא זוכר אותם אז זה בסדר).

שאלה 29

נשים לב ש:

ולכן:

נקבל:

שאלה 30

השגיאה אינסופית כי הוא תהליך לא יציב - המקדמים של המכנה שלו לא כולם מאותו הסימן.

חלק ג’

שאלה 31

לפי משוב יחידה:

כאשר נקראת פונקציית הרגישות.

שאלה 32

לפי משוב יחידה, מקשרת בין ל-, בין ל- (במינוס), וגם בין ל- (במינוס).

שאלה 33

לפי יציבות BIBO, יציבה BIBO אם לכל כניסה חסומה למערכת נקבל יציאה חסומה.

שאלה 34

נשים לב שהפולינום האופייני הוא:

הפולינום לא הורביץ ולכן המערכת בחוג סגור לא יציבה.

שאלה 35

נשים לב שיש צמצום לא יציב בין ו- (עבור ) ולכן המערכת בחוג סגור לא יציבה.

שאלה 36

נשים לב ש- ולכן המערכת בחוג סגור יציבה.
נזכור כי:

במקרה של כניסת מדרגה, ולכן:

במצב מתמיד:

נקבל:

ניתן גם היה לראות זאת לפי שגיאה עבור אות ייחוס מדרגה.

שאלה 37

נשים לב ש:

לפי יציבות של פולינום ממעלה שלישית, נראה כי לא הורביץ ולכן המערכת בחוג סגור לא יציבה:

שאלה 38

את הבקר נוכל לרשום גם כ:

מחפירות של שניר על בקר , המכנה בפונקציות החוג הסגור הופך להיות , ולכן:

שאלה 39

את הבקר נוכל לרשום:

באותו אופן כמו סעיף קודם:

חלק ד’

שאלה 40

לפי ייצוג מג”ש:

לפי חיתוך עם הציר המדומה, עלינו לבדוק מתי:

נציב ונקבל:

ניתן לראות שעבור נקבל:

ולכן נקבל שהמג”ש חוצה את הציר המדומה ב- .

שאלה 41

נשים לב שהאפסים והקטבים הם:

לכן, בהנחה ו- , על הציר הממשי יש מג”ש ב- וגם ב- , ולפיכך ענף אחד מסתיים ב-.
מאחר ויש שני אפסים, ואף אחד מהם הוא לא סוף של הענפים בציר הממשי, נסיק שהם מהווים גם סוף של ענפי המג”ש.
נשים לב גם שיש עודף קטבים של , ולכן לפי אסימפטוטה במג”ש, יצאו שלושה ענפים בזוויות , כאשר את כבר ידענו.

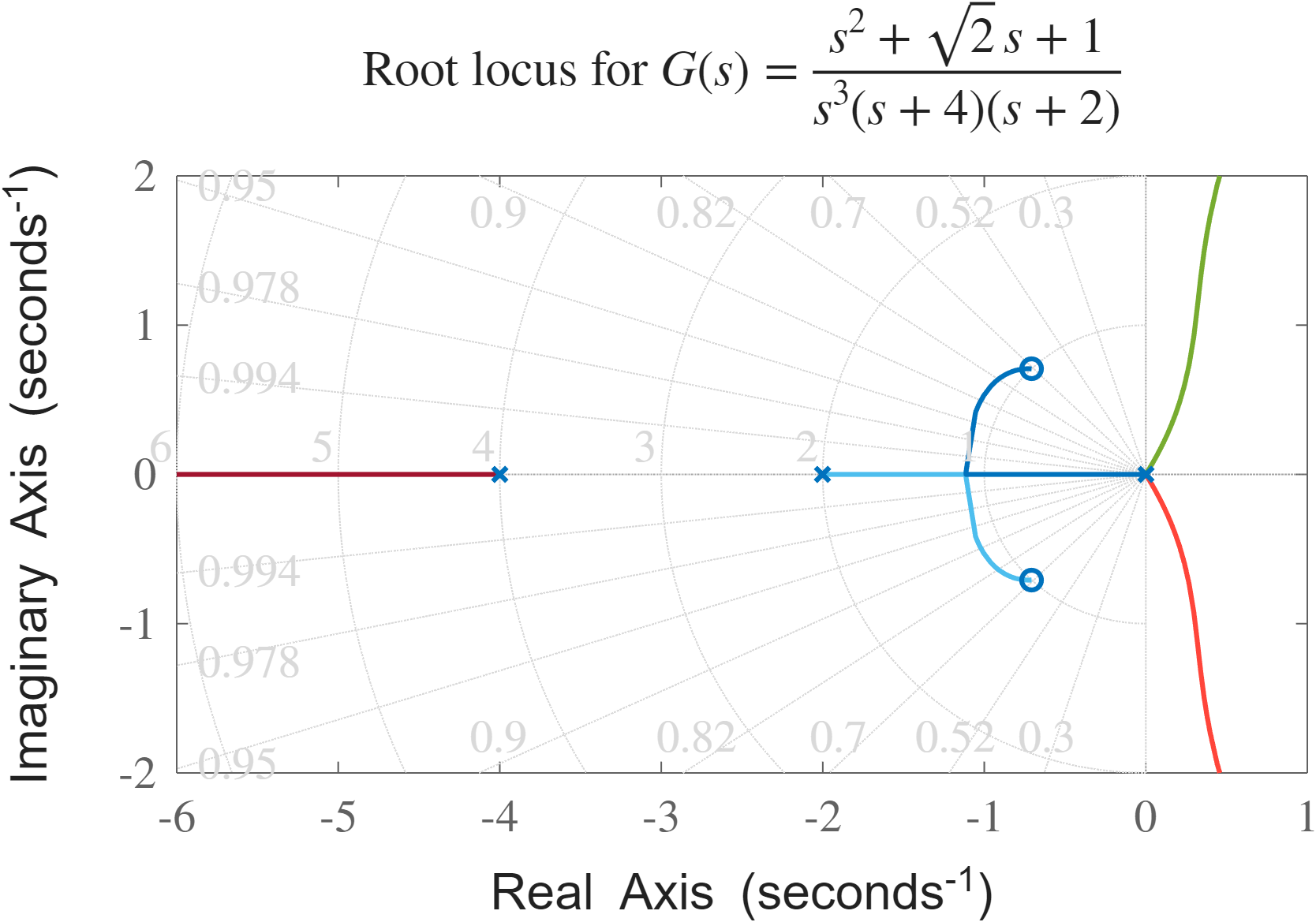
מג”ש של המערכת הנתונה.

שאלה 42

נוכל לכתוב גם בצורה:

נשים לב שאין עודף קטבים - , כך שאין אסימפטוטות. נסיק שכל הענפים מסתיימים באפסים (שהם כולם ).

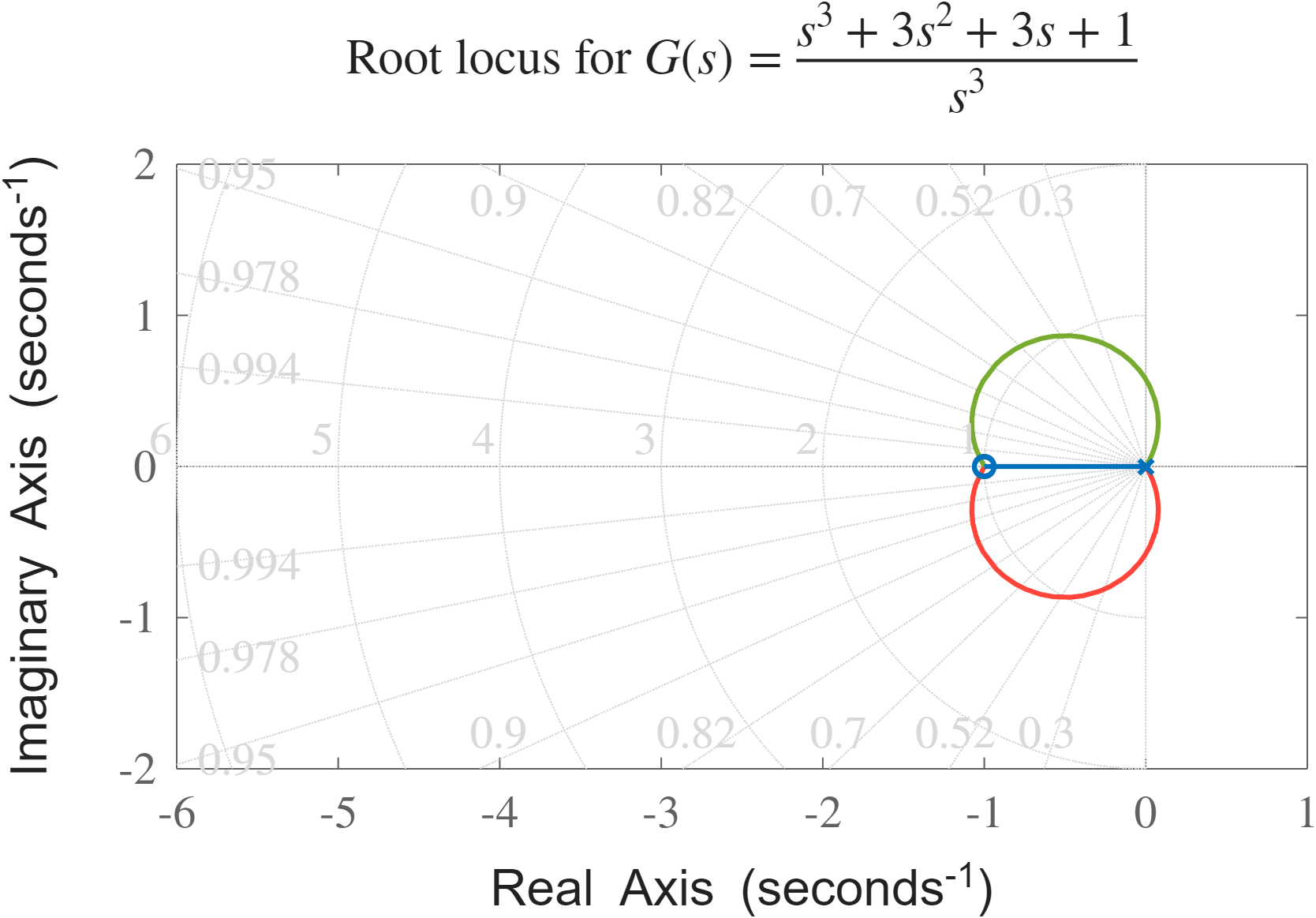
מג”ש של המערכת הנתונה.

שאלה 43

לפי אסימפטוטה במג”ש, במקרה של אסימפטוטות עם הגבר בקר חיובי:

הזוויות ו- לא נכללות בקבוצת ענפים זו, כך שלא אמור להיות ענפים על הציר הממשי במקרה זה. נסיק שגרף ג’ לא נכון.

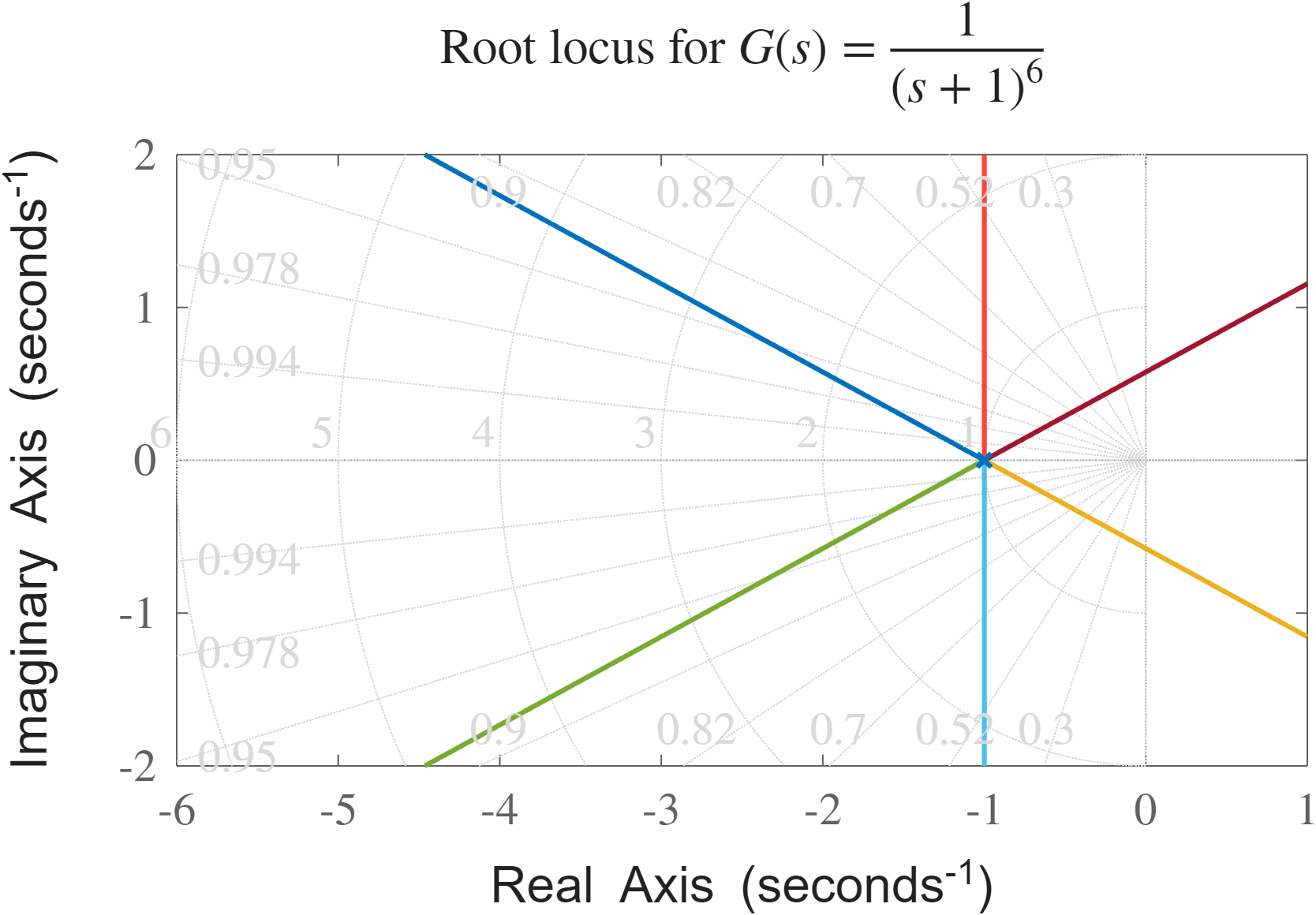
המג”ש הנכון במקרה של אסימפטוטות.

שאלה 44

המרכז מסה יהיה בין ל- (אבל יותר קרוב ל-). בנוסף, משאלה קודמת, אנו יודעים את הכיוונים של האסימפטוטות. נסיק כי גרף ג’ הוא הנכון.

שאלה 45

נשים לב שמאחר ויש אסימפטוטות ושני אפסים, חייבים להיות קטבים. לפיכך, יש קטבים בראשית, כך שהמג”ש המתואר באמת מתואר עבור הגבר חיובי (אחרת היינו רואים ענף על הציר הממשי שיותר מ-).
נסיק שישנו טווח קטן של -ים עבורו כל הקטבים של המערכת יהיו ב-LHP הפתוח, ולפיכך ניתן יהיה לייצב את החוג הסגור.

שאלה 46

נשים לב שישנם אסימפטוטות ו- ענפים שמסתיימים בעיגולים, כך שישנם אפסים. לכן, יש קטבים.

שאלה 47

קודם כל נוודא שמירקין לא רמאי ובאמת המג”ש הנתון הוא עבור הגבר חיובי. נשים לב שיש שתי אסימפטוטות ומאחר ויש אפס אחד, יש קטבים, ששניים מהם בראשית. סבבה, הכל טוב, ההגבר חיובי.
קטבים ב- זה קטבים שנמצאים על מעגל ברדיוס . מאחר והמג”ש עובר דרך מעגל ברדיוס זה, ונקודת החיתוך כנראה תהיה די קרובה, מבחינת מרחק מהציר המדומה, לקוטב על הציר הממשי. נסיק שלפי דינמיקה דומיננטית, הקטבים בתדירות לא דומיננטיים ביחס לקוטב על הציר הממשי.

שאלה 48

יש עודף קטבים של ולכן ישנם שלוש אסימפטוטות ב- ו-. בהגברים גבוהים האסימפטוטות האלו מובילות את הענפים ל-RHP, מה שאומר שהמערכת לא תהיה יציבה. מוסבר יותר בהרחבה בהתנהגות מג”ש בהגברים גבוהים.

חלק ה’

שאלה 49

ממשוב יחידה, חייב להתקיים:

(זה למה קוראים ל- רגישות משלימה).
לכן, הדרישה הנתונה לא יכולה להתקיים במשוב יחידה.

שאלה 50

לפי ביצועים בתגובת מעבר, נרצה לקרב כמה שיותר את לנקודה הקריטית , מה שיגדיל את הרוחב-פס של ולפיכך יאיץ את תגובת המעבר של החוג הסגור.

שאלה 51

לפי עיקרון הארגומנט של קושי, מקיף את הראשית פעמים, כאשר ו- הם מספר האפסים והקטבים בתוך , בהתאמה.

שאלה 52

מאחר ול- יש שני אפסים, ו- מכיל רק אחד מהם, נסיק שלפי עקרון הארגומנט, מאחר ו- מקיף את הראשית פעמיים:

כאשר הוא מספר השורשים של בתוך . לכן:

שאלה 53

לפי פונקציית ה-return difference, מאחר והחוג הפתוח יציב, אין לו קטבים ב- (), ולכן:

לפי האיור לא מקיפה את הנקודה הקריטית ולכן:

נסיק שהמערכת בחוג סגור יציבה.

שאלה 54

הבקר פרופורציונלי לא משפיע על מספר הקטבים/אפסים בחוג הפתוח , אז ל- יש מספר קטבים לא יציבים כמספר הקטבים הלא יציבים של . כלומר, . כדי ש- , אנו צריכים שהגרף הפולארי של יקיף את הנקודה הקריטית נגד כיוון השעון פעם אחת. לפי ניתוח חוגים, נוכל לנתח את המערכת עם הנקודה הקריטית , ואז עלינו לבדוק תחומים:

• עבור , אין הקפות. באסה.
• עבור , יש הקפה אחת נגד כיוון השעון. מגניב.
• עבור , אין הקפות.
  נסיק כי:

שאלה 55

באותו אופן כמו סעיף קודם, רק הפעם נשים לב שנתון ש- יציב, אז אנו מחפשים עבור איזה אין הקפות. ניתן לראות שזה קורה עבור . נסיק כי:

כדי למצוא את בתחום היציב של המערכת, נשים לב כי לפי משפט הערך הסופי:

עבור כניסת מדרגה 𝟙, מתקיים , כך ש- ולכן:

ניתן לראות מהגרף ש- ולכן:

נסכם:

שאלה 56

אנו יודעים שהשהייה (זמן מת) לא משפיע על הגבר תגובת התדירות, אלא רק על הפאזה. ללא ההשהייה, המערכת היא מסדר ראשון פשוט , כך שבתדירות הפאזה שלה אמורה להיות (לפי כללי אצבע לדיאגרמות בודה). באיור אנו רואים שב- מתקיים , כך שנסיק שההשהייה שלנו היא:

שאלה 57

לפי עודפי הגבר ופאזה:

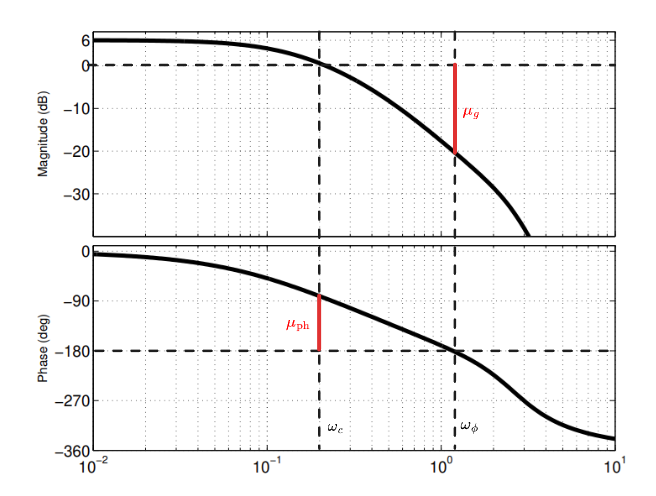
עודפי הגבר ופאזה של המערכת הנתונה.

לכן:

שאלה 58

לפי עודפי הגבר ופאזה:

תנאי זה אף פעם לא מתקיים. כלומר, אי אפשר להגדיר עודף הגבר לאינטגרטור (או שאפשר לומר ).
מבחינת עודף פאזה, נשים לב ש:

נמצא כי:

ולכן עודף הפאזה:

לכן העודף זמן מת:

שאלה 59

באותו אופן כמו שאלה קודמת, נשים לב ש:

אין הפותר משוואה זו ולכן אין השהייה שתוציא את המערכת מיציבות:

שאלה 60

נשים לב ש:

ולכן, לפי עודף זמן מת:

כלומר, כל השהייה קטנה תוציא את המערכת מיציבות.

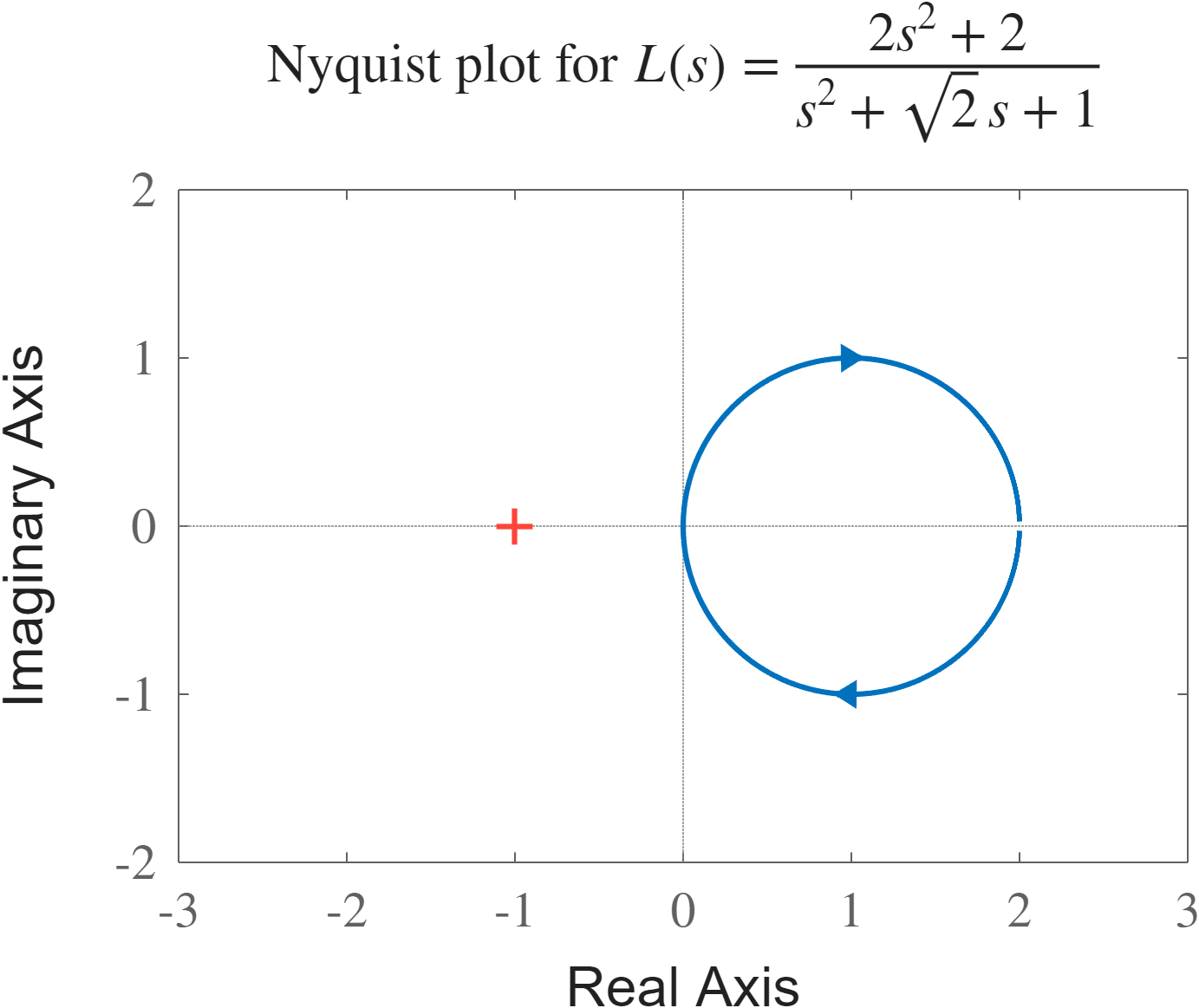
דיאגרמת נייקוויסט של המערכת הנתונה.

שאלה 61

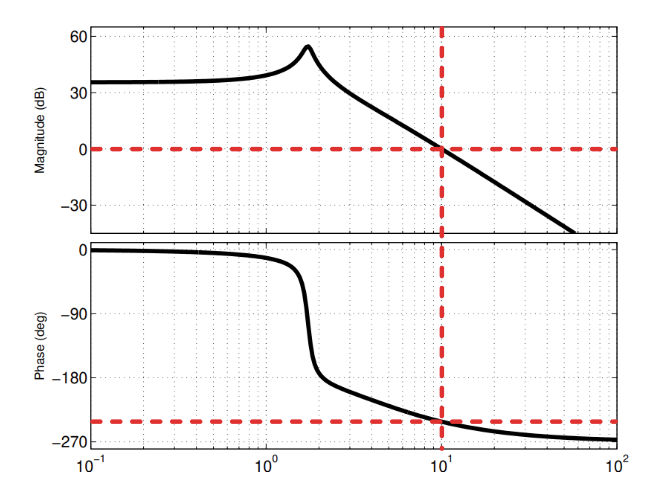
דיאגרמת בודה הנתונה.

נשים לב שכבר מתקיים , כל מה שנותר לנו לעשות זה ש-, אחרת, לפי בקרי קידום ופיגור, עקום נייקוויסט שלו יקיף את הנקודה הקריטית, וזה יוציא את המערכת מיציבות (נתון ש- כבר יציבה). מאחר ו-, נבחר בקר קידום (שלא ישפיע על ) שיקדם את הפאזה של ללפחות מעל .

שאלה 62

נתון כי המערכת כבר יציבה. לכן, לא נרצה שבתדירות המעבר הפאזה שלה תהיה מתחת ל- כי זה יוציא אותה מיציבות (קריטריון נייקוויסט, יוסיף עוד סיבוב סביב הנקודה הקריטית). נשים שאם נעלה את תדירות המעבר ליותר מ- (ע”י בקר יחסי, שהוא לא משנה את גרף הפאזה), הפאזה המתאימה תהיה יותר קטנה מ-, אז נסיק כי הוא תדירות ההגבר המקסימלית.

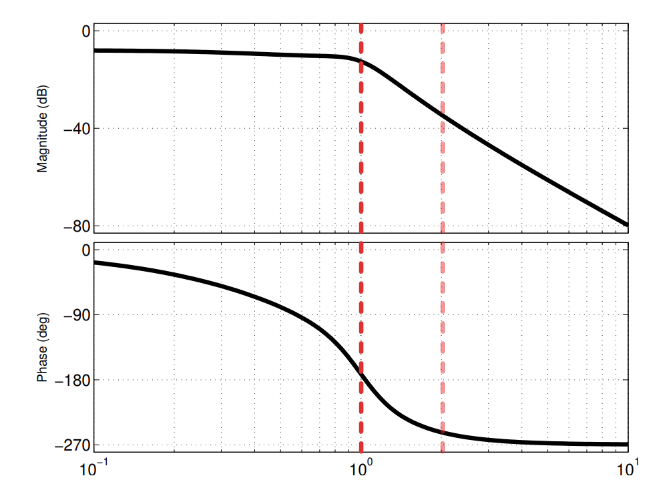
גרף הבודה הנתון.

שאלה 63, 64

בשני הבקרים אנו לא רוצים לשנות את ההגבר ב-. מהצורה שלהם, ההגבר ב- נשאר , אז נבחר כדי לקיים את הדרישה.

שאלה 65

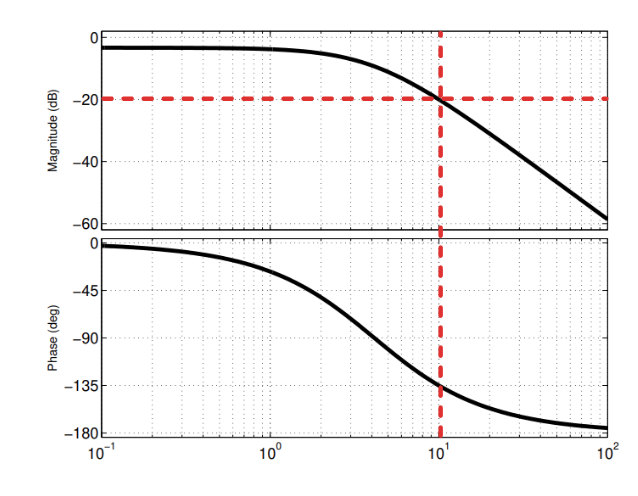
גרף בודה הנתון.

לתהליך הנתון שנסמנו אין תדירות מעבר. אם נרצה שתדירות המעבר תהיה , עלינו להגביר אותו ב- כפי שניתן לראות מהאיור. כלומר, נבחר בקר פרופורציוני עם:

נשים לב גם שבמצב הנוכחי עודף הפאזה (בתדירות המעבר הרצויה) הוא:

לכן, לאחר הוספת בקר פיגור, נישאר עם כנדרש. כיוון שרוצים שגיאת מצב מתמיד אפס, נבחר את הבקר פיגור עם :

נבחר גם כי אנו רוצים לשמור על ההגבר בתדר זה:

נקבל את הבקר:

שאלה 66

הזמן המת יוסיף לנו פאזה בגודל בתדירות המעבר, כך שהפאזה בתדירות זו תהיה כעת:

כך שעודף הפאזה עומד כעת על:

ביחד עם בקר פיגור, נצטרך להוסיף בקר קידום שיקדם את הפאזה ב:

לפי הגרף לבחירת , נבחר , כך שבקר הקידום יהיה (נבחר עדיין ):

ולכן הבקר כעת יהיה:

שאלה 67

יש כמה דרכים לפתור את זה, ביניהם לפי נייקוויסט. נפתור דווקא כמו בשאלה 22. נשים לב של- יש עודף קוטב יחיד, ב- יש עודף של שני קטבים, וב- יש עודף של שלושה קטבים. נתאים למג”שים המתאימים לפי מספר האסימפטוטות שלהם:

שאלה 68

נזכור שבמקרה של משוב יחידה עם בקר פרופורציוני פשוט, מתקיים (במקרה הרצוי של ) שזה תאכלס .
נשים לב ש- מקיף את הנקודה הקריטית (פעמיים) ולכן זה כמו לומר שעבור ה- הנתון, למערכת יש קטבים ימניים. המקרה היחידי המתואר במג”ש בו יש קטבים ימניים הוא:

שאלה 69

כמו בשאלה 22, ניתן לראות של- יש עודף קוטב יחיד ולכן הוא מתאים לגרף בודה עם שיפוע של :

מבחינת ו-, ההבדל העיקרי הוא התהודה שמגדילה את בערכי תדירות מסוימים. לכן, מאחר וברוב התדירויות אנו רואים ש- , נסיק כי:

שאלה 70

נשים לב שיש לנו קטבים מרוכבים. ממרחקם מהראשית נסיק כי הם כולם מיוחסים לתדירויות באזור . לכן זו תהיה תדירות הפינה של גרף הבודה הגבר שלהם - ההגבר יתחיל לרדת באזור , שזה מתאים ל-.

שאלה 71

נשים לב שבתהליך תדירות מעבר הפאזה היא . כלומר, בתדירות זו נוכל להגיע לסף יציבות בעזרת זיגלר-ניקולס. בתדירות זו ההגבר של הוא , ולכן:

בנוסף, זמן המחזור יהיה:

לכן לפי זיגלר-ניקולס, נבחר:

כך שהבקר PI הוא: