MCS1_HW003 תרגיל בית 3

קורס	מכניקת מיקרו-מערכות
מספר קורס	00350041

עידו פנג בנטוב
CLASSIFIED
CLASSIFIED

---

---

חלק א’

נתון קפיץ הבנוי מקרות סיליקון רתומה. אורך הקורה , עוביה , ועומקה (). הקורה רתומה מצד שמאל והיא שוקעת בכיוון האנכי בלבד. נתון כי הקורה מיוצרת ממצע של Single Crystalline Silicon (SCS) ואורכה מתלכד עם הכיוון הקריסטלוגרפי . ראו איור HW3.1 לסכמת הגיאומטריה.

איור HW3.1: סכמת הקורה הרתומה.

שאלה 1

מה המודול האלסטי הרלוונטי לבעיה?

פתרון:
מודול האלסטיות של SCS בכיוון נמצא להיות ^[Hall, J. J. (1967). Electronic Effects in the Elastic Constants of n -Type Silicon. Physical Review, 161(3), 756–761. https://doi.org/10.1103/PhysRev.161.756].

שאלה 2

מהי שקיעת קצה הקורה עקב משקלה העצמי?

פתרון:
לפי טבלת שקיעות, השקיעה בקצה היא:

כאשר הוא העומס המפורש כתוצאה מהמשקל העצמי.
נוכל לפתח זאת גם ממשוואת אוילר-ברנולי. בהנחה ו- פועל כלפי מטה ו- פונה כלפי מעלה:

נבצע אינטגרציה:

לא מתפתחת זווית או שקיעה בריתום, כך ש- :

בחתך בקצה אין כוחות גזירה או מומנט, ולכן:

נציב בחזרה ב-(HW3.2):

נמצא את השקיעה בקצה :

וזו התוצאה שקיבלנו ב-(HW3.1).

בהנחה והצפיפות של הסיליקון היא , גודל העומס המפורש הוא:

כאשר הוא למעשה גודל שטח החתך של הקורה.

שאלה 3

כיצד מושפעת השקיעה משינויים בעומק הקורה ?

פתרון:
המומנט השני של החתך הרלוונטי כאן הוא:

נציב ב-(HW3.1):

נציב את (HW3.4):

לפיכך, השקיעה בקצה הקורה לא תלויה בעומק הקורה.

שאלה 4

מהו היחס בין שקיעת קצה הקורה לאורכה?

פתרון:
מ-(HW3.5) נסיק שיחס הגדלים הוא:

שאלה 5

כיצד ישתנה יחס זה אם כל הממדים הגאומטריים יגדלו פי ?

פתרון:
מ-(HW3.6) ניתן לראות שיחס זה יגדל פי .

שאלה 6

מתוך ההרצאה, או לפי מוצקים 2, מאמץ הכפיפה המתפתח יהיה:

מהפיתוחים ב-סעיף ב’ ראינו שתגובת הריתום:

מאחר ו-, נסיק בריתום:

ולכן:

מאמץ הכפיפה המקסימלי יתרחש היכן ש- מקסימלי (או מינימלי אם אכפת לנו רק מגודל המאמץ), כלומר, ב- :

סימן תוצאה זו תלוי במיקום: בקצה העליון של הריתום תתקבל מתיחה.

שאלה 7

נתון:

מצאו את תכונות החומר הדרושות (צפיפות ומודול אלסטיות) והציבו ערכים אלו בסעיפים ב’, ד’, ו’.

פתרון:
הראנו כבר שמודול האלסטיות הרלוונטי הוא:

בנוסף, הצפיפות של סיליקון SCS היא ^[Arblaster, J. W. (2018). Selected values of the crystallographic properties of elements. A S M International.]:

נציב ב-(HW3.5), (HW3.6), (HW3.7):

שאלה 8

מהו היחס בין מאמץ הכפיפה המקסימלי בקורה לחוזק הסיליקון ?

פתרון:
תחת משקל עצמי, אנו מקבלים את היחס:

שאלה 9

כיצד ישתנה יחס זה באם כל הממדים הגאומטריים יגדלו פי ?

פתרון:
מתוך (HW3.7), נסיק שהיחס הוא:

לפיכך, אם כל הממדים הגאומטריים יגדלו פי , היחס לעיל יגדל פי .

שאלה 10

כעת מחברים לקצה הקורה מסה ריבועים שרוחבה וגבהה (עומק המסה היות וכל ההתקן מיוצר שכבת ה-device של מצע SOI).

איור HW3.2: הקורה עם מסה מרוכזת בקצה.

הניחו שהמסה היא מסה נקודתית המרוכזת בקצה הקורה והזניחו את מסת הקורה.

מהי שקיעת קצה הקורה עקב משקל המסה?

פתרון:
מאחר ונוכל להתייחס למסה כמסה נקודתית, הבעיה שקולה לקורה שלוחה הפועל עליה כוח ב- כלפי מטה. כוח יהיה משקל המסה:

השקיעה תחת מצב זה תהיה:

נציב (HW3.9):

נציב את :

נקבל:

נציב ערכים:

שאלה 11

האם היה מוצדק להזניח את מסת הקורה?

פתרון:
מהשוואת הפתרונות של שאלה 7 ושאלה 10 מתקבל שהשקיעה עקב המסה גדולה פי מהשקיעה עקב המשקל העצמי. הזנחת המשקל העצמי תוביל לשגיאה של כ- בתזוזה, ולכן ההנחה היא בקירוב סביר רק אם דרישת הדיוק רופפת.

שאלה 12

מהי התדירות הטבעית של המערכת?

פתרון:
אם נבצע את הפישוט של המערכת למערכת אלסטית פשוטה, נוכל להיעזר ב-(HW3.11) כדי להגדיר את קשיחות המערכת כ:

מסת המערכת (בהזנחת המשקל העצמי) היא:

ולכן התדירות הטבעית:

נקבל:

נציב ערכים:

שאלה 13

כיצד הייתה התשובה לסעיפים ו- משתנה אם לא היינו מניחים שהמסה היא נקודתית?

פתרון:
כאשר אנו מניחים שהמסה נקודתית, אנו לא רק מזניחים את העובדה שהעומס בקצה הקורה הוא למעשה עומס מפורש - אנו מזניחים גם את המומנט אינרציה של המסה. לפיכך, התדירות הטבעית של המערכת תהיה יותר נמוכה כי למעשה ה- גדל ב-.

חלק ב’

באיורים הבאים מופיעים משפעלים עם קפיצים מסוג serpentine. נתון כי הקשיחות של כל קורה באורך היא . חשבו מה הקשיחות השקולה (בכיוון התנועה) של כל מבנה. הניחו כי אזורי החיבורים הינם קשיחים מאוד בהשוואה לקורות.

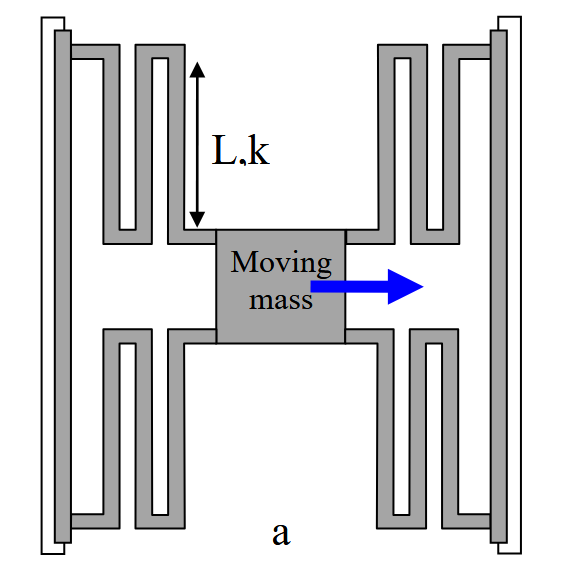
איור HW3.3: משפעל א’.

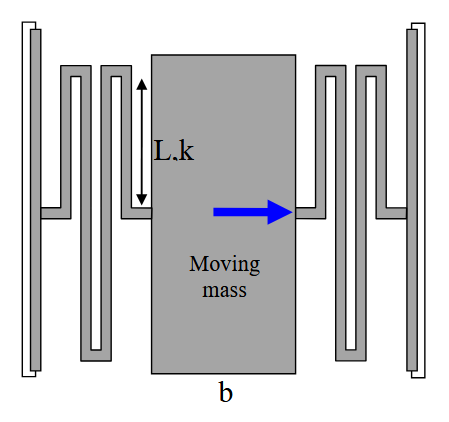
איור HW3.4: משפעל ב’.

פתרון:
עבור משפעל א’, ניתן לזהות 4 קפיצים מחוברים במקביל (ביחס למסה):

מעגל שקול למשפעל א’.

כל אחד מהקפיצים האלה בעל קשיחות זהה, והוא מורכב מ-3 קורות, כל אחת בעלת קשיחות לכפיפה . מאחר והקורות מחוברות באופן מקופל (folded), הן מתפקדות כקפיצים המחוברים במקביל. לכן קשיחות כל אחת מארבעת הקפיצים היא:

חיבור של ארבעה קפיצים כאלו במקביל נותן את סך הקשיחות:

עבור משפעל ב’, ניתן לזהות שני קפיצים מחוברים במקביל (ביחס למסה):

מעגל שקול למשפעל ב’.

כל אחד מהקפיצים מורכב מארבעה קורות מחוברות בטור, שתיים באורך ושתיים באורך . אנחנו מכירים שהקשיחות לכפיפה בקורה נתונה ע”י:

ולכן אם אורך הקורה הוא , הקשיחות קטנה פי ! כלומר, סך הקשיחות של כל קפיץ היא:

חיבור שני קפיצים כאלה במקביל נותן את סך הקשיחות:

חלק ג’

מסה נסמכת על מתלה מיקרו-מכני, המורכב משבע קורות גמישות, המחוברות בעזרת שני מחברים קשיחים, ו- (Flying Bars). שש קורות מתוך השבע, הינן זהות ואורכן וקורה אחת בעלת אורך . לכל הקורות רוחב ועומק .

כוח יכול לפעול כלפי מטה רק באחת מהנקודות . והזזה של אותה נקודה בכיוון הכוח תסומן ב-. (לשם הדגמה, באיור מופיע הכוח שפועל בנקודה ).

המערכת הנתונה.

בכל הסעיפים הבאים, הניחו כי רוחב קורות החיבור זניח ביחס לאורך הקורות הגמישות. בכל סעיף נתונות תשובות סופיות. יש לשחזר תוצאות אלה, בצורה מפורטת (דג”ח והצבות מתאימות) כפי שנלמד בכיתה.

שאלה 1

עבור כוח הפועל בנקודה (בלבד!), מהי השקיעה וזווית הסיבוב בנקודות ?

פתרון:
נפרק את הבעיה למקטעים. מערכת שקולה היא:

תרשים קפיצים שקול למערכת לעיל.

נזכור ממשוואה (3.1) מההרצאה שהשקיעה הכללית עבור כוח בקצה קורה באורך היא:

במקרה של flying bars, ממשוואה (3.6) ראינו ש:

לכן הקשיחויות של הקורות הנתונות הן

עבור הפעלה של ב- בלבד, השקיעה ב- (וגם בכל שאר הנקודות) היא:

מבחינת הזווית, מאחר והקשיחות הצירית של הקורה גדולה בהרבה מהקשיחות שלה לכפיפה, עבור מקטעים ו- הקורות לא יכולות להסתובב:

שאלה 2

עבור כוח הפועל בנקודה (בלבד!), מהי השקיעה וזווית הסיבוב בנקודות ?

מתוך (HW3.19) נסיק כי:

לפיכך:

לכן השקיעה ב- (וגם ב-):

בחתך ב- ישנו גם כן כוח גזירה (וגם מומנט, אבל הוא מתקזז עם המומנט שהקשיחות הצירית של הקורות מפעילה), ולכן השקיעה בו תהיה זהה לסעיף הקודם:

מבחינת זוויות, כמו בסעיף הקודם:

שאלה 3

עבור כוח הפועל בנקודה (בלבד!), מהי השקיעה וזווית הסיבוב בנקודות ?

פתרון:
כמו בסעיפים קודמים, ניתן להראות ש:

מבחינת השקיעה ב-, מתוך (HW3.19) ו-(HW3.20):

ולכן:

לכן השקיעה ב-:

מבחינת הזוויות:

אבל הפעם, מכיוון שנקודה מחוברת ל- אך ורק ע”י קורה אחת, כן מתפתחת זווית ב- לפי (HW3.17):

שאלה 4

אם כוח הגרביטציה פועל באותו כיוון כמו הכוח , מה השפעת הגרביטציה על השקיעה? הסבירו.

פתרון:
המשוואות (HW3.17) - (HW3.21) ליניאריות, ולכן ניתן להפעיל עקרון סופרפוזיציה. נסמן את המשקל העצמי ככוח קבוע הפועל באותה נקודה שבה אנו מפעילים את . אזי השקיעה הכוללת היא:

כאשר היא הקשיחות השקולה של המקטע הרלוונטי: , או . לפיכך הגרביטציה מוסיפה הזזה סטטית קבועה . כלומר, כל התוצאות שנגזרו עבור עדיין תקפות, ורק יש להוסיף להן היסט סטטי המתאים למשקל העצמי של הנקודות הרלוונטיות.