MDN1_003 בורגי הנעה ובורגי הידוק

→ קודם: MDN1_002הבא: MDN1_004 ←

מושגי יסוד בברגים

האיור הבא מציג את המושגים הבסיסיים בתבריגים:

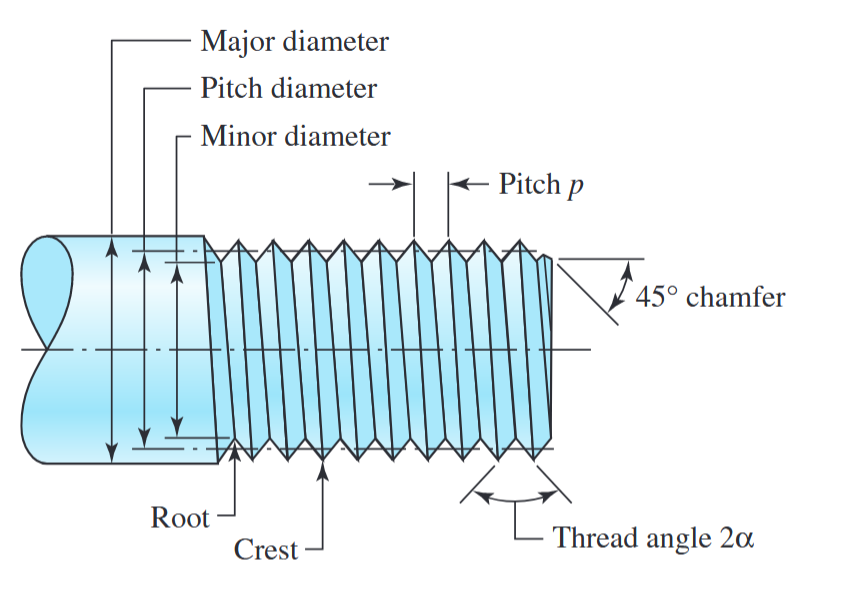
מושגי יסוד בתבריגים. שיאי ההברגה (crests) ושורשי ההברגה (roots) כאן מוקצנים - הם בד”כ מיושרים או מעוגלים ביצירת הבורג. (Budynas et al., 2015).

באיור מופיע:

• קוטר חיצוני/ראשי (major diameter) .
• קוטר פסיעה (pitch diameter) .
• קוטר פנימי (minor diameter) .
• פסיעה (pitch) - המרחק בין כריכות שונות.
• שיפוע (chamfer) וזווית הברגה (thread angle) .
• שיא הברגה (crest) ושורש הברגה (root).

בנוסף, אמנם פחות נפוץ, אבל יכולים להיות לבורג מספר התחלות:

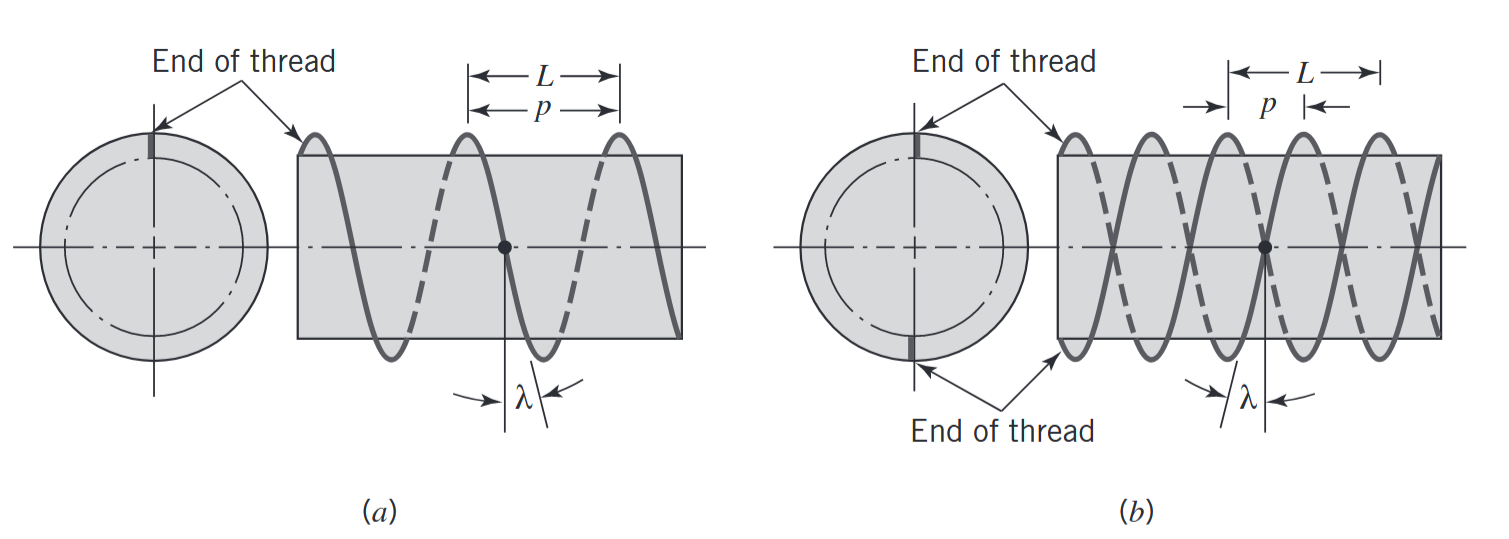
בורג עם (a) התחלה אחת; (b) שתי התחלות. (Juvinall & Marshek, n.d.).

• המעלה (lead) היא המרחק שהאום מתקדמת בסיבוב אחד, והוא נתון ע”י המשוואה: כאשר הוא מספר ההתחלות.
• זווית המעלה היא הזווית בין האנך לכיוון הבורג לכיוון ההברגות עצמן.

כל הברגים מיוצרים לפי כלל יד ימין אלא אם כן נדגיש אחרת. כלומר, אם מסובבים את הבורג עם כיוון השעון, הבורג מתקדם לכיוון האום.

ברגי הנעה

בורג הנעה הוא מכשיר להפיכת תנועה סיבובית לקווית (ולעתים להיפך). באיור הבא מופיע מַגְבֵּהַּ (jack) שעיקרון הפעולה שלו עובד על בורג הנעה.
![[Budynas_et_al._-2015-_Shigley_s_mechanical_engineering_design_page_429_1-removebg-preview.png|250]]

ה- Joyce worm-gear screw jack. (Budynas et al., 2015).

באיור הבא מופיע בורג הנעה עם תבריג ריבועי והתחלה אחת עם קוטר ממוצע , פסיעה , זווית התחלה . הבורג נתון תחת עומס לחיצה בכיוון הציר שלו.

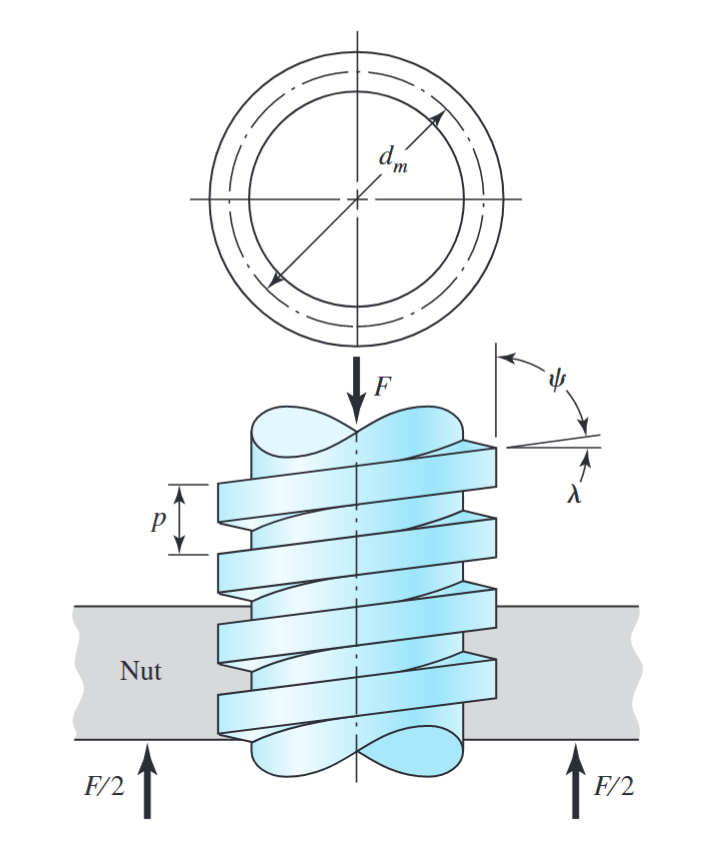
חלק מבורג הנעה. (Budynas et al., 2015).

נאמר שאנו מעלים את העומס כאשר אנו מקדמים את הבורג נגד כיוון הכוח החיצוני, ושאנו מורידים את העומס כאשר אנו מקדמים את הבורג עם כיוון הכוח החיצוני (תאכלס, אנחנו לא באמת מקדמים את הבורג, אלא את הלוח/הגוף אליו הוא מתוברג).

נרצה למצוא ביטוי למומנט הנדרש כדי להעלות את עומס זה, ועוד ביטוי למומנט הנדרש להורדת עומס זה. כלומר, אנו רוצים ביטויים לכמה כוח/מומנט אנו צריכים להפעיל כדי להבריג פנימה או החוצה את הבורג.

ראשית. נדמיין שאנו פורסים הברגה יחידה של הבורג, לסיבוב אחד:

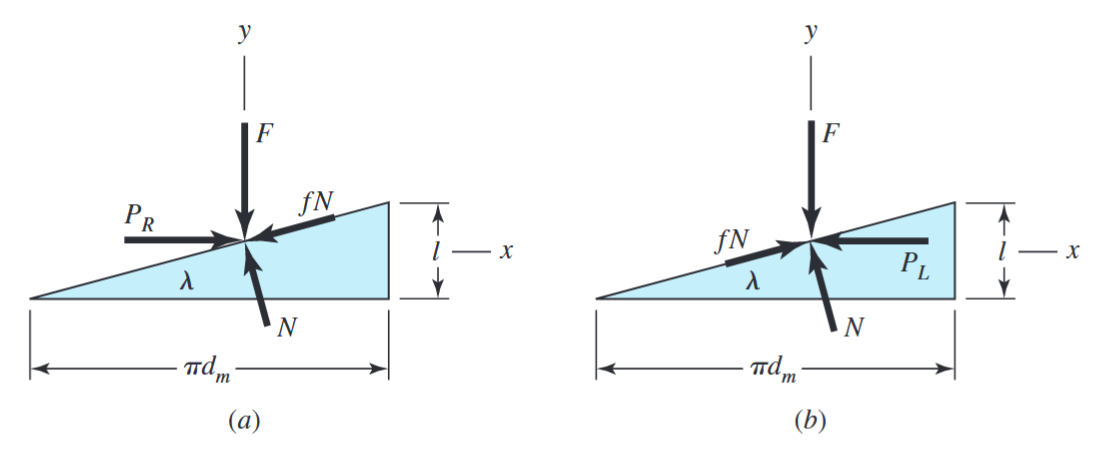
דג”ח על (a) העלאת העומס; (b) הנמכת העומס. (Budynas et al., 2015).

צד אחד של ההברגה הופך להיות היתר של משולש ישר זווית שהבסיס שלו הוא הקוטר הממוצע של ההברגה והגובה שלו הוא המעלה. נבטא את סכום הכוחות הציריים הפועלים על הבורג ב-. כדי להגדיל את העומס, כוח פועל ימינה, וכדי להקטין את העומס, כוח פועל שמאלה. כוח החיכוך הוא הכפל של מקדם החיכוך עם הכוח הנורמלי , ופועל בכיוון ההפוך לתנועה. המערכת בשיווי משקל תחת פעולת כוחות אלו, ולכן כדי להעלות את העומס, לפי משוואות שיווי משקל:

באותו אופן, כדי להוריד את העומס:

עבור כל אחד מהמקרים, נבודד את ו-:

מגאומטרייה, אנו יודעים ש- , ולכן:

נרצה לתרגם את כוחות אלו למובנים של מומנטים. המומנט הנדרש בקצה הבורג, כלומר במרחק מהמרכז, כדי להפעיל את הוא:

ה- הוא המומנט הנדרש:

• להתגבר על החיכוך.
• להעלות את העומס.

באותו אופן, המומנט הנדרש להוריד את העומס הוא:

למומנטים אלו נקרא המומנטי הנעה.

משוואות אלו תקפות עבור הברגות ריבועיות, אבל אלו הברגות אידיאליות שיותר קשה ליצר אותן. להלן סוגי הברגות שונות:

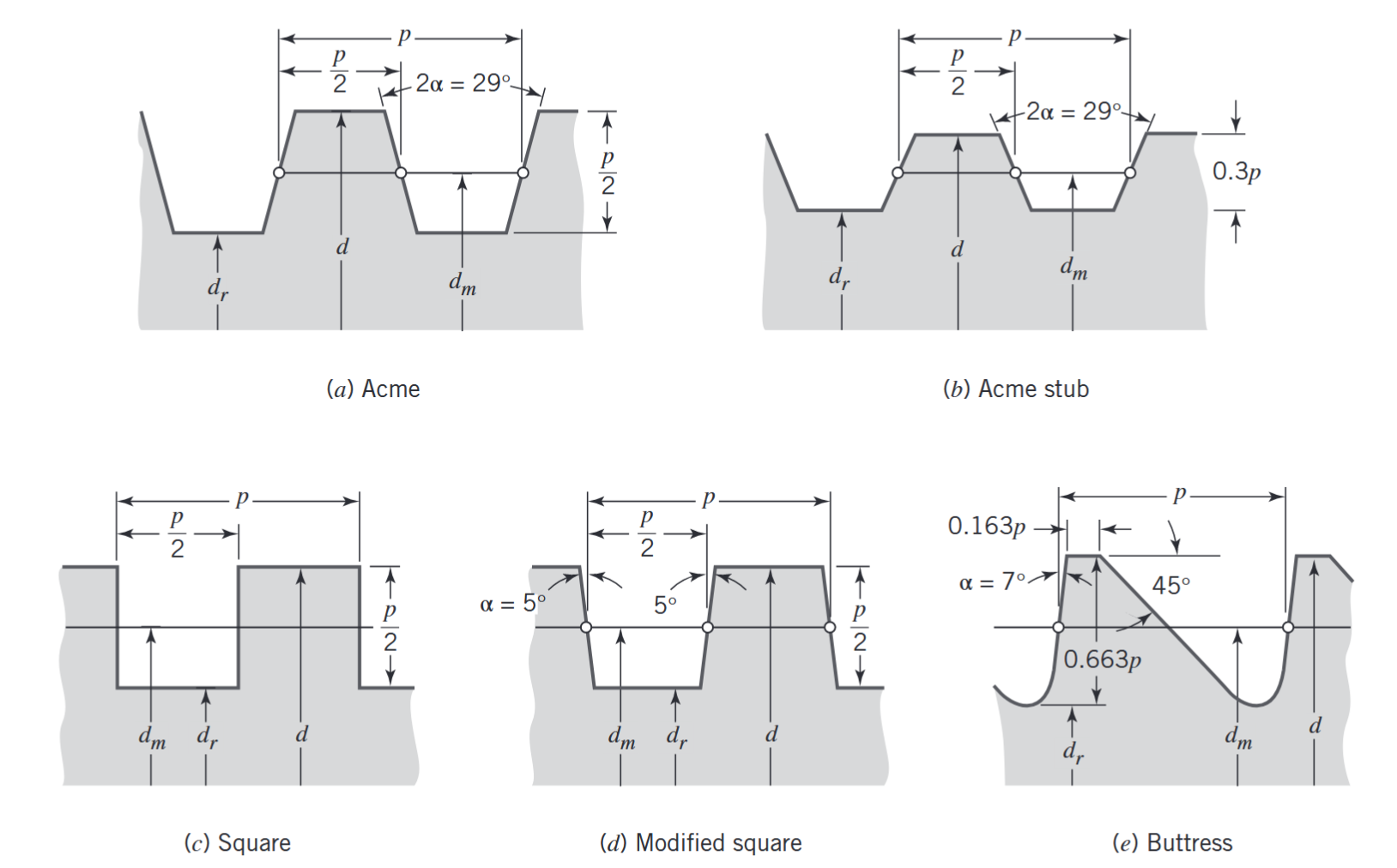
ברגי הנעה בצורות שונות. הקוטר הוא הקוטר המוצע ושווה בערך ל- . (Juvinall & Marshek, n.d.).

במקרים אלו, להבדיל מתבריג ריבועי, יש זווית הברגה , מה שמעלה את כוח החיכוך בהברגה (משהו מתחלק ב-, לא חקרתי לעומק). כאשר נתייחס לזווית זו, נקבל את שמקרה הכללי:

נעילה עצמית

במצבים מסוימים בהם המעלה גדולה או החיכוך נמוך, נמצא כי העומס ירד לבד ויגרום לבורג להסתובב בלי שום כוח חיצוני. במקרים אלו, המומנט ממשוואה (SH8-2) יהיה שלילי או אפס. כאשר נקבל מומנט חיובי ממשוואה זו, נאמר שהבורג ננעל עצמית (self-locking). לכן, התנאי לנעילה עצמית היא:

כעת, נחלק את שני הצדדים של משוואה זו ב-. נשים לב ש- , כך שנקבל:

קשר זה אומר שנעילה עצמית מתרחשת כאשר מקדם החיכוך בהברגה גדול מה- של זווית המעלה.

נצילות בורג הנעה

הגדרה: נצילות בורג הנעה

נצילות בורג הנעה היא היחס בין המומנט הנעה ללא חיכוך למומנט הנעה המציאותי:

כאשר הוא המומנט הנעה ללא חיכוך - .

עבור המקרה הכללי, ממשוואה (JM10.3), אם , נקבל ש:

מאחר והחיכוך הוזנח, ביטוי זה הוא המומנט הדרוש רק כדי להעלות את העומס. נציב ביטוי זה ומשוואה (JM10.4) בהגדרה לנצילות הבורג כדי לקבל ביטוי כללי:

במקרה הפרטי של תבריג ריבועי:

ערכים ל- ניתן למצוא בטבלה 8-5.

חיכוך בצווארון

העברת התנועה הקווית לסיבובית ולהיפך דורש לרוב שני מעברים: בין הבורג לאום, (שנידון לעיל) ובין הבורג לחלק הנע/סטאטי (תלוי אם האום נייחת או ניידת). מעבר זה מתרחש בצווארון (collar) והינו מקור נוסף לחיכוך שמגדיל את מומנטי סיבוב הבורג. מומנט החיכוך הנוסף ניתן לביטוי כ:

כאשר הוא מקדם החיכוך בצווארון ו- הוא קוטר הצווארון הממוצע (אנו מניחים ששם מתרכז העומס).

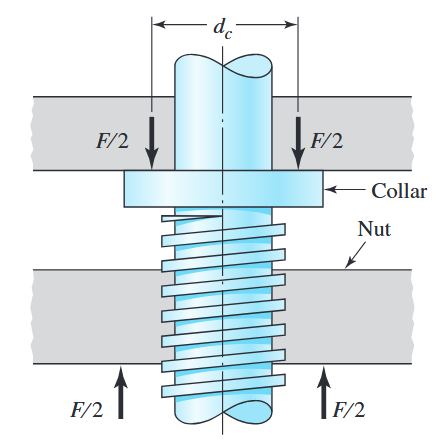
צווארון עם מקדם חיכוך וקוטר . (Budynas et al., 2015).

לכן, נוכל להכליל עוד יותר את משוואות (JM10.3) עם התחשבות בחיכוך זה:

ערכים ל- ניתן למצוא בטבלה 8-6.

מאמצים בקנה

המאמצי פיתול בבורגי הנעה ניתנים לחישוב מהפיתול שהם חווים. בקוטר הפנימי:

המאמץ הצירי בגוף הבורג כתוצאה מלחיצה:

לכן, מבחינת הקנה, נוכל לבדוק את תקינותו ע”י הצבת מאמצים אלו בקריטריון פון מיזס:

כך שמקדם הביטחון הוא:

מאמצים בכריכות

מאמצים שונים מתפתחים בכריכות עצמן של הבורג:

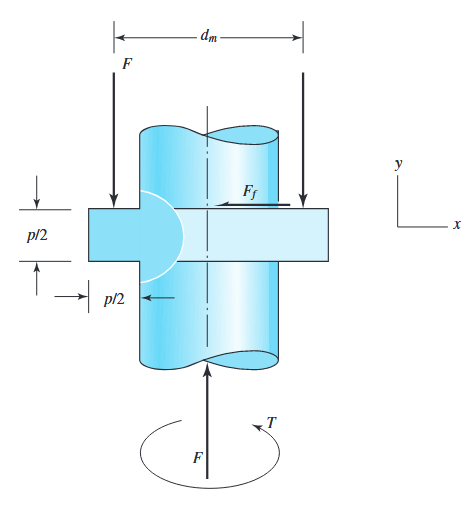
גאומטרייה של תבריג ריבועי, לטובת חישוב מאמצים בהברגה. (Budynas et al., 2015).

ישנם שלושה סוגי מאמצים שאנו נבחן בכריכות:

• מאמץ מעיכה . מאמץ זה הוא מאמץ מיוחד המתפתח בשורש התבריג, ובכללי מתפתח בעוד גאומטריות של מגע בין משטחים קמורים וקעורים - במקרה שלנו, בין הכריכות והמצעים. זהו נושא עצום בפני עצמו, שכאן פשוט נתייחס אליו כעוד מאמץ שצריך לבדוק אותו מול קבועים שנמצאו בניסויים.
• מאמץ צירי עקב כפיפה.
• מאמץ גזירה עקב כפיפה.

מאמץ המעיכה (bearing stress/pressure) באיור לעיל הוא:

כאשר הוא מספר הכריכות המשולבות - מספר הכריכות בנשיאת העומס, כולל כריכות מהתחלות נוספות. אם למשל הוא גובה האום בו משולבות כריכות הבורג, אז:

מבחינת מקדם ביטחון, ישנם ניסויים שלפיהם ניתן לעבוד באופן:

כאשר את ניתן להוציא מטבלה 8-4. במקרים בהם בורג ההנעה והאום עשויים מאותו החומר ניתן להניח כי של חומר הבורג ומקדם ביטחון מספק .

המאמצים הנורמליים והמאמצי גזירה (המקסימליים):

מבחינת מקדם הביטחון למאמצים אלו:

במקרה ולא מדובר בתבריג ריבועי, עלינו להתייחס גם לזווית ההברגה :

כאשר לא משתנה כי יוצא שההשפעה של הזווית מתקזזת במונה ובמכנה.

מאמץ בכריכה הראשונה

במציאות העומס לא מתחלק שווה בין הכריכות המשולבות. ניסויים ואנליזות מראים שהכריכה המשולבת הראשונה נושאת מהעומס הכולל, השנייה ב-, השלישית כ- (סה”כ 3 כריכות נושאות מהעומס), הכריכה השביעית לא נושאת בעומס כלל.
לכן, במשוואות לעיל, כאשר יש יותר משלוש כריכות משולבות (), מציבים במקום את עם . למשל, עבור מאמץ מעיכה:

עבור נציב ללא שינויים.

ברגי הידוק

ישנם שני תקנים דומיננטיים בעולם ההברגות - תקן ותקן . ניתן להיעזר ב-MDN1_C8 טבלאות ברגים כדי למצוא את ההגדרות לברגים שונים.

לפי התקן האמריקאי , הנקרא בקיצור Unified:

• תבריגים בזווית שן .
• השיאים של התבריגים יכולים להיות שטוחים או מעוגלים, והשורשים מעוגלים.
• מבדילים בין ו-, הראשון לתבריגים גסים והשני לעדינים (בהמשך נסביר על ההבדל). ישנו גם בו שורש התבריג מעוגל לטובת עמידות משופרת להתעייפות.
• התבריג מזוהה ע”י הגדרת הקוטר הנומינלי הראשי, ואחריו מספר הכריכות לאינץ’, ואחריו סוג התבריג - או .
• בתבריגים הקטנים מ- קוטרו המזהה של התבריג מסומן ע”י מספר סידורי: וכו’.

האיור הבא מתאר את הגאומטרייה של פרופילי המֶּטְרִית ו- מתקן :

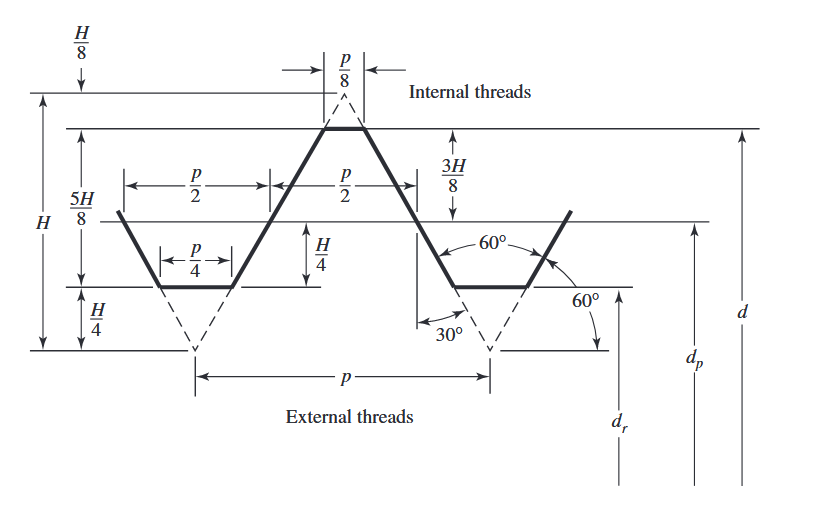
פרופיל בסיס למטרית ו-. הגודל הוא פשוט . (Budynas et al., 2015). בנוסף, מתקיים וגם .

פרופיל ה- המטרי הוא הפרופיל הבסיסי לתקן עם:

• תבריגים בזווית שן .
• השיאים שטוחים והשורשים מעוגלים.
• מסומן ע”י האות וגודל הקוטר המזהה: , וכו’.
• התבריג העדין מזוהה ע”י האות וגודל הקטור המזהה, כפול גודל הפסיעה: וכו’.

תוצאות ניסויי מתיחת מוטות הברגה מראים שהחוזק שלהם שווה ערך למוט לא מתוברג בעל קוטר שהוא ממוצע קוטר הפסיעה והקוטר הפנימי של התבריג. לכן מוצגים בטבלאות ברגים גם שטח המתיחה שהוא שטח שקול לשטח החתך של התבריג מבחינת חוזק מתיחה.

הברגה עדינה והברגה גסה

הברגה עדינה.

בהברגה עדינה:

• הבורג חזק יותר ( גדול יותר).
• באותו מומנט סגירה ההברגה העדינה מייצרת כוחות הידוק גבוהים יותר.
• נהוג ליישום במקומות בהם קיים “עידוד” לפתיחת ברגים - במערכות רוטטות, רכב, וכו’.
• המעלה הנמוך יכול לשמש לכוונון עדין יותר במתקנים.

הברגה גסה.

בהברגה גסה:

• הרכבה ופירוק מהירים יותר.
• עמידה יותר, פחות רגישה ל”התברגות עצמית”, לכן טובה יותר, בין היתר, עבור ברגים קטנים, בהם ההברגה עדינה ורגישה גאומטרית.
• לחומרים רכים - כי כוחות ההידוק קטנים יותר.

מחבר בורגי

האיור הבא הוא שרטוט של בורג עם ראש משושה סטנדרטי.

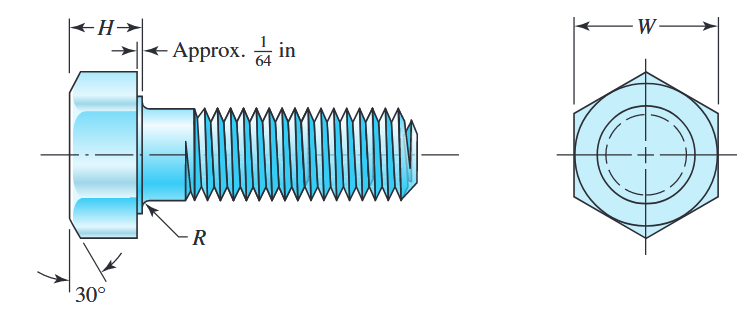
בורג הידוק עם ראש משושה. (Budynas et al., 2015).

הריכוזי מאמצים מתרחשים בפילט (fillet), בתחילת ההברגה (runout), ופילט שורש ההברגה. האורך המתוברג של ברגי Unified, כאשר הוא הקוטר הנומינלי (הקנה) הוא:

ועבור הברגים המטריים:

כאשר המידות במילימטרים.

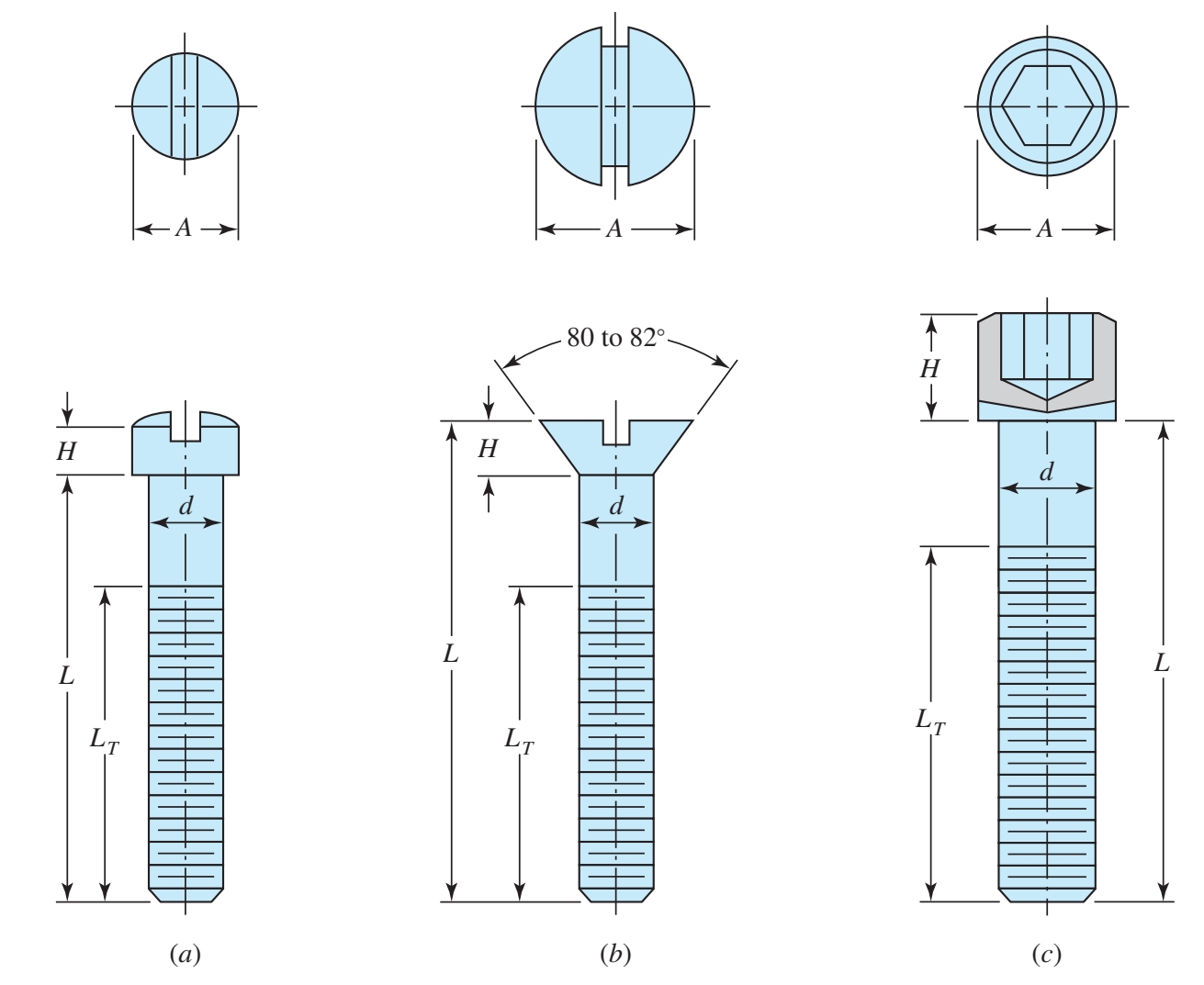
ראשי ברגים טיפוסיים: (a) ראש fillister (רֹאשׁ עָגֹל); (b) ראש שטוח; (c) ראש שקע משושה. (Budynas et al., 2015).

אורך הבורג האידיאלי הוא בו רק אחת או שתי כריכות (או לפי הקורס, 1.5 עד 3 כריכות) יוצאות מהצד השני של המחבר לאחר חיזוקו. להברזות עצמן (החורים בהם עשו את ההברגה) עלולים להיות פינות חדות לאחר שהבריזו אותן. אלו יכולים לחרוט את הפילט וכתוצאה מכך להגדיל את ריכוז המאמצים. לכן, לרוב שמים דסקיות (washers - שַׁיְיבָּה) מתחת לראש הבורג כדי למנוע זאת. לפעמים יש צורך גם בדסקיות מתחת לאום.

קשיחות הבורג

מחברים בורגיים מאפשרים חיבור חזק דיו לשאת עומסים גבוהים, כאשר נדרש גם חיבור שניתן לפרקו ולהרכיבו ללא הרס. חיבור זה יודע לשאת עומסים ציריים, עומסי כפיפה ופיתול, או כל שילוב שלהם. להלן מוצג חיבור בורגי מפלדה מחוסמת עם דסקיות. מחבר כזה עלול להיות מסוכן מאוד אם לא תוכנן והורכב ע”י איש מקצוע.

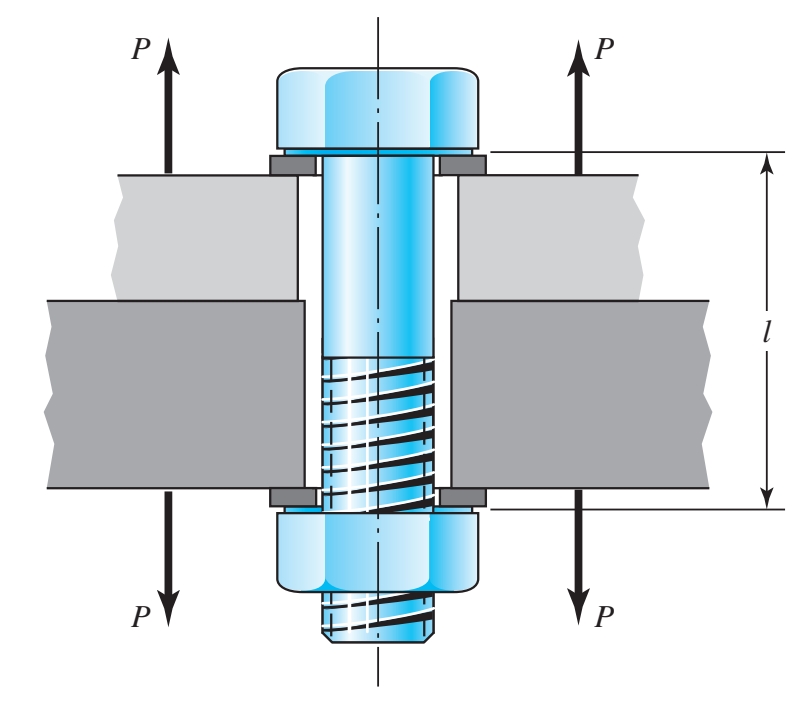
מחבר בורגי הנתון לעומס מתיחה ע”י הכוחות . שימו לב להוספה של דסקיות למחבר. שימו לב גם לגובה שבו ההברגה מתחילה בתוך גוף המחבר - יש לה חשיבות עצומה, במיוחד אם המחבר צריך גם לעמוד בעומסי גזירה. (Budynas et al., 2015).

מטרת הבורג הידוק היא להדק שני חלקים ביחד, מה שנקרא מחבר בורגי. עומס ההידוק מאריך את הבורג; העומס נוצר מהסיבוב של האום/בורג עד שהבורג הגיע לסף האלסטיות שלו. אם האום לא משתחרר, כוח המתיחה על הבורג מתקבע, והוא נקרא כוח הידוק התחלתי או כוח דריכה התחלתי (preload or clamping force). כוח הידוק זה קיים ללא קשר אם העומסים החיצוניים פועלים על המחבר או לא. כמובן שאם נוצרה מתיחה בבורג, על החלקים נמצאים בלחיצה.

הערה:

כאשר מחזקים, כדאי, אם אפשר, להחזיק את ראש הבורג קבוע ולסובב את האום. כך התבריג עצמו לא ירגיש את החיכוך שלו עם ההברזה.

אורך האחיזה (grip) של מחבר הוא העובי הכולל של החומר המהודק. באיור לעיל זהו סכום האורכים של שני החלקים והדסקות. ישנם מקרים (שנראה מיד בהמשך) בהם הוא מחושב באופן טיפה שונה.

הקשיחות של הבורג באזור ההידוק יכלול שני חלקים - החלק המתוברג והחלק הלא מתוברג. לכן, קבוע הקשיחות שאנו נגדיר עבורו שקול לחיבור שני קפיצים בטור:

לכן, הקשיחות של הבורג תהיה מצורה זו. נותר לנו רק להגדיר היטב את האורכים והשטחים של כל אחד מהחלקים השונים במתיחה.

להלן מפורט אופן מציאת החוזק של מחבר בורגי:

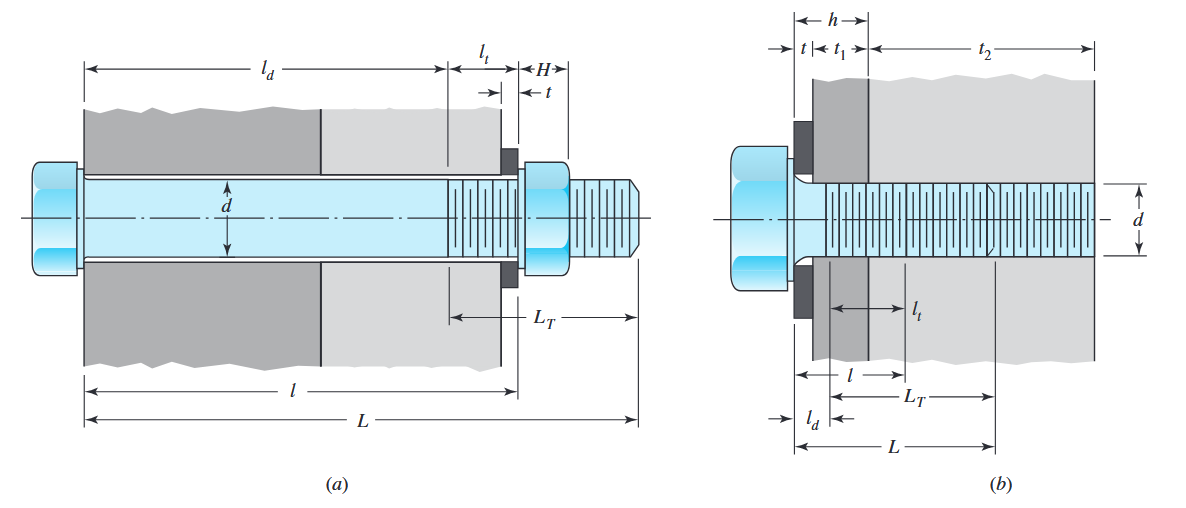
מחבר בורגי טיפוסי; (a) מחבר בורגי משני הצדדים. (b) מחבר בורגי מצד אחד. (Budynas et al., 2015).

בהינתן מחבר בורגי בקוטר ופסיעה . הפרמטרים עליו ניתן למצוא מ:

• עובי דסקה - MDN1_A31-33 טבלאות אומים ודסקות.
• עובי אום - MDN1_A31-33 טבלאות אומים ודסקות.
• אורך האחיזה (grip) :
  • במקרה (a), הוא עובי כל החומר בין הפנים של הבורג לפנים של האום, כפי שמתואר באיור.
  • במקרה (b): כאשר מוגדר באיור.
    • אורך המחבר הוא:
    • במקרה (a):
    • במקרה (b):
    • אורך מתוברג לפי (SH8-13) ו-(SH8-14).
    • אורך החלק הלא מתוברג במחבר:
    • אורך החלק המתוברג במחבר:
    • שטח החלק הלא מתוברג:
    • שטח החלק המתוברג - מ-MDN1_C8 טבלאות ברגים.

לאחר שיש לנו את כל הפרמטרים הרצויים, נוכל לחשב את קשיחות הבורג :

כאשר הוא מודול יאנג של החומר, שניתן למצוא מטבלה 8-8.

קשיחות מצע החיבור

בחלק הקודם מצאנו את קשיחות הבורג באזור ההידוק. בחלק זה נרצה לחשב את הקשיחות של המצעים (members) בו. עם שני ערכים אלו נוכל לדעת מה קורה בכלל המחבר הבורגי כאשר הוא נתון למתיחה חיצונית.
מאחר ואזור הלחיצה במצעים נוטה להתפשט באופן לא אחיד בין ראש הבורג לאום, די קשה למצוא נוסחה סגורה לקשיחות המצע ללא ניסויים מקדימים. אבל, ישנם מקרים בהם ניתן לקבל קירוב טוב לפילוג המאמצים במצעים, שמהם פיתחו שיטות לקירוב הקשיחות.
השיטה שנעבוד לפיה טוענת שהנפח המועמס ליד ראש הבורג הוא קונוס קטום בזווית , והוא מועמס בלחץ אחיד.

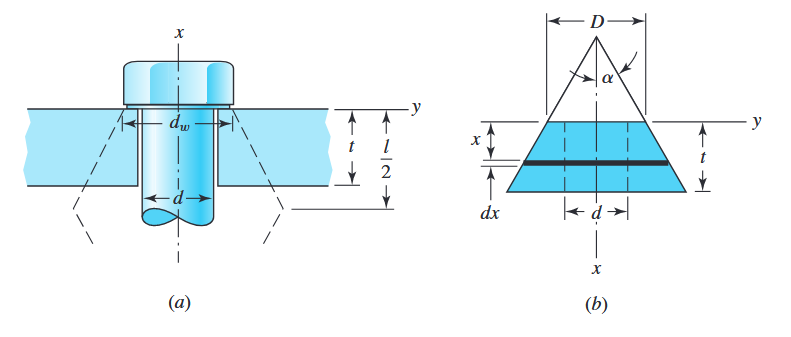
קירוב הקונוס הקטום ל: (a) ראש הבורג; (b) גאומטריית הקונוס הקטום. (Budynas et al., 2015).

מניתוח אלמנט דיפרנציאלי של הקונוס הקטום וסכימה לאורך כל עובי המצע נקבל שקבוע הקשיחות של הקונוס הקטום עם הקדח:

כאשר הוא הקוטר החיצוני הקטן של הקונוס הקטום (כפי שמופיע באיור לעיל).
עבור מצע מפלדה, נניח כי (הזווית נמצאה מניסויים, בדרך כלל בין , אנו נניח ש- ):

בהנחה ו-עובי המצע הוא מחצית מאורך המחבר, , ולדסקה עובי סטנדרטי יחסית לבורג , נקבל כי:

עבור זוג מצעים, אנו צריכים להתייחס לשני המצעים כקפיצים מחוברים בטור, כי:

לכן, אם שני המצעים מאותו החומר:

ישנו חישוב יותר זריז עבור זוג מצעים מאותו החומר וכשהבורג סטנדרטי - חישוב מקורב זה נקרא קירוב גרין, ועל פיו:

עם הקבועים ו- שספציפיים עבור סוג המצעים, וניתן למצוא אותם בטבלה 8-8.
עבור שאר המקרים, חייבים לחזור למשוואה (SH8-20) כדי למצוא את קשיחות המצעים.

חוזק בורג

במפרט סטנדרטים לברגים, החוזק נתון לפי גדלי SAE או ASTM מינימליים, חוזק מוכח מינימלי, עומס מוכח מינימלי וחוזק מתיחה מינימלי. מפרטים אלו מוצגים ב-MDN1_C8 טבלאות ברגים.
עומס מוכח (proof load) הוא העומס (כוח) המקסימלי שבורג יכול לעמוד בו ללא דפורמציה פלסטית. חוזק מוכח הוא המאמץ המתאים לעומס המוכח והשטח מתיחה לדפורמציה של בקנה הבורג.

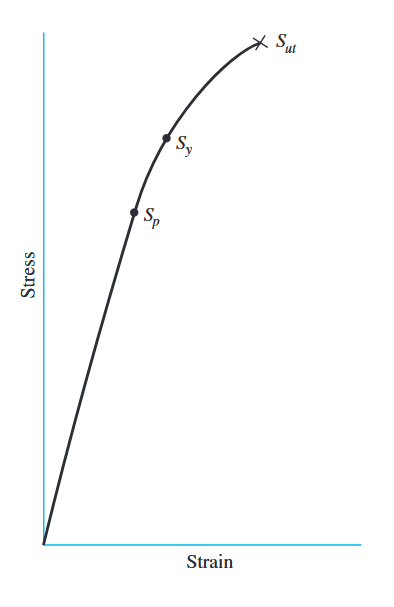
דיאגרמת מאמץ-עיבור טיפוסית לברגים עם חוזק מוכח , חוזק כניעה , וחוזק מתיחה . (Budynas et al., 2015).

מפרט SAE נמצא בטבלה 8-9. הברגים מדורגים לפי החוזק מתיחה שלהם, כאשר הנקודה העשרונית משמשת לווריאציות באותה רמת החוזק.

מפרט ASTM נמצא בטבלה 8-10. ב-ASTM האזור המתוברג בברגים קצר יותר כי ASTM עוסקים לרוב עם מבנים; מחברים מבניים לרוב מועמסים בגזירה, שם נרצה שההברגה לא תהיה על מישור הגזירה (ריכוז מאמצים).

מחבר מתיחה - עומס חיצוני

נביט מה קורה כאשר מאמץ מתיחה חיצוני, כפי שמתואר באיור הבא, מופעל על מחבר בורגי:

מחבר בורגי הנתון לעומס מתיחה ע”י הכוחות . (Budynas et al., 2015).

אנו מניחים כמובן שכוח ההידוק, לו אנו קוראים ההידוק ההתחלתי , יושם באופן נכון ע”י הידוק האום לפני ש- הופעל. נשתמש בסימונים:

• הידוק התחלתי - .
• סך כוח המתיחה על המחבר - .
• כוח מתיחה חיצוני לבורג - .
• החלק של שנתמך ע”י הבורג - .
• החלק של שנתמך ע”י המצעים - .
• סך העומס על הבורג - .
• סך העומס על המצעים - .
• השבר של העומס החיצוני שנתמך ע”י הבורג - .
• מספר הברגים במחבר - .

אם ברגים מחלקים את העומס החיצוני באופן שווה, אז:

העומס הוא בלחיצה, מה שגורם לחיבור להימתח או להתארך (עיבור) באורך מסוים . נוכל לקשר את התארכות זו ע”י הקשיחות כאשר נזכור ש- הוא הכוח חלקי העיבור:

או:

מאחר ו- , נקבל:

כאשר

נקרא מקדם הקשיחות של המחבר או בקצרה, מקדם המחבר. סך העומס על הבורג הוא

וסך הכוח על המצעים הוא:

תוצאות אלו תקפות כל עוד המצע בלחיצה, כלומר כל עוד .

הפעלת כוח חיצוני וחימום

במידה והמחבר הבורגי נמצא גם תחת חימום, ישנה השפעה של עיבור תרמי על החלקים במחבר. במידה ו- ו- הם מקדמי ההתפשטות של המצע והבורג בהתאמה (שניתן למצוא מטבלה 3-3, ו- הוא הפרש הטמפרטורות, משוואות העיבור של הבורג והמצע הופכים להיות:

כמו מקודם, עדיין , ולכן הכוח בבורג והכוח במצע הם:

העמסה סטטית של מחבר בורגי עם הידוק התחלתי

משוואות (SH8-24) ו-(SH8-25) מתארות את הכוחות במחבר בורגי עם הידוק התחלתי. לכן, העומס מתיחה בבורג הוא:

לכן, מקדם ביטחון לכניעה בבורג, לפי חוזק מוכח :

או פשוט:

אם יש שילוב מאמצים בבורג, אז נשתמש במאמץ השקול לפי פון מיזס , ואז מקדם הביטחון יהיה:

כיוון שלרוב נעמיס בורג במאמצים הקרובים לחוזק המוכח, מקדם הביטחון לא גדול בהרבה מ-. עוד מקדם ביטחון לכניעה הוא מה שנקרא מקדם עומס , שמיושם רק על העומס כדי להימנע מעומס יתר. הצבת מקדם ביטחון זה בביטוי שפיתחו ל- לעיל מניב:

מה שאומר ש:

נזכור גם שאם הכוח במצע מתאפס , מתקבל ניתוק במחבר שמשמעו חשיפת הבורג למלוא הכוח החיצוני, שנחשב ברוב המקרים לכניעת המחבר והוא מצב לא רצוי. לכן, נרצה שתמיד:

נוכל להגדיר מקדם ביטחון נגד ניתוק:

מתוך כל החישובים האלה וניסויים שונים, המלצה כללית היא הידוק כללי של מהעומס המוכח, אם מדובר בחיבורים שהולכים לפרקם ולחברם מספר פעמים. אם מדובר במחבר תמידי, אז אפשר אפילו להדק עד מהעומס המוכח. לכן, עבור עומסים סטטיים ואפילו מחזוריים (להתעייפות), מומלץ הידוק התחלתי

כאשר הוא העומס המוכח, שניתן לחישוב מ:

כאשר את הוא החוזק המוכח שניתן למצוא מ-MDN1_C8 טבלאות ברגים.

אטם במחבר בורגי

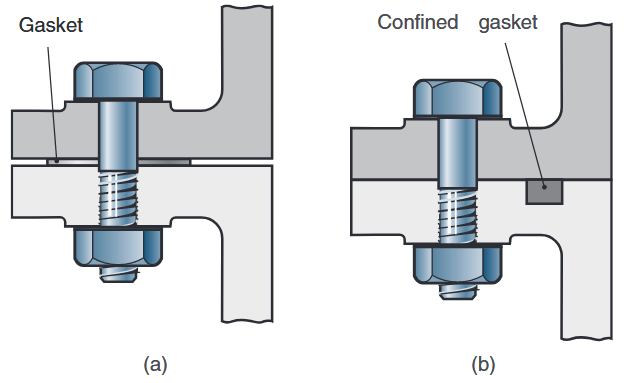
אטמים במחבר בורגי. (a) אטם לא תחום (unconfined gasket); (b) אטם תחום (confined gasket). (Schmid et al., 2014).

אם אטם בשטח ( עבור gasket) קיים במחבר, הלחץ באטם נמצא ע”י חילוק הכוח במצע ע”י השטח של האטם לבורג. לכן, עבור ברגים:

בהינתן לחץ הנדרש לאטימה , עלינו לדרוש שכוח ההידוק במצעים חזק מספיק כדי לקיים את , כלומר:

עם מקדם ביטחון להפעלת עומס, זה אומר שהלחץ באטם המינימלי:

אנו מבדילים בין שני סוגים של אטמים המופיעים בשרטוט לעיל. במקרה (a) מתואר אטם לא כלוא, שהוא אטם שפיזית מפריד בין שני המשטחים. אם לאטם זה קשיחות נמוכה יחסית לקשיחות הבורג או המצעים, יוצא כך שמהחיבור בטור של הקשיחויות ש- , ואז:

מה שאומר שהבורג חשוף למלוא הכוח החיצוני !

מה הקטע עם הקשיחות שוב?

נדמיין שהאטם הוא ספוג:

תחת לחיצה, הקשיחות של המצעים והספוג היא תאכלס רק הקשיחות של הספוג (כל עוד הוא לא נלחץ עד הסוף). לכן, כאשר מוסיפים בורג למחבר, הבורג, ולא המצעים, יספוג את רוב העומס.

במקרה (b), האטם תחום בתוך אחד מהחלקים, כך שקיים מגע ישיר בין שני המשטחים מעל ומתחת לאטם, ונוכל להזניח אותו כאשר מחשבים את הקשיחויות במחבר.

במחברים עם אטמים אחידות הלחץ על האטם היא קריטית. כדי לשמור על אחידות מספיקה, אנו נתכנן ברגים צמודים לא יותר משישה קטרים בין לבין על עיגול הברגים:

סוגי אטמים שונים.

כדי לשמור גישה לפירוק עם מפתח (wrench), הברגים צריכים להיות ממוקמים לפחות שלושה קטרים בין לבין. לכן:

כאשר הוא קוטר עיגול הברגים ו- הוא מספר הברגים.
בנוסף, לא נמקם את הברגים במרחק הקטן משני קטרים מקצה החלק.

התעייפות מחבר בורגי

מחברים בורגיים הנתונים למאמצים מחזוריים ניתנים לניתוח ע”י השיטות שפותחו בפרק קודם. טבלה 8-16 מכילה מקדמי ריכוז מאמצים לפילט מתחת לראש הבורג וגם לתחילת התבריג על הבורג. גדלים אלו כבר מתוקנים לרגישות חריץ, ולכן מופיע שם .
רוב הברגים מיוצרים בשיטת rolled threads. בשיטה זו, לוקחים את מאמץ סף ההתעייפות מטבלה 8-17 ללא צורך בתיקונים נוספים. כלומר, אין להגביר את המאמצים במקדם כיוון ש- מכיל את היבטי שיטת הייצור ורגישות לצורה הגאומטרית.
כאשר אין בידנו מניסויי ברגים, נעשה שימוש בנתוני חומר גלם ונחשב את בעזרת מקדמי מארין. במקרה זה יש לעשות שימוש בפקטור ריכוז מאמצים בהתעייפות בהתאם לשיטת עיבוד הבורג.

עבור המקרה הכללי של הידוק התחלתי קבוע ועומס חיצוני לבורג התונד בין ו-, הבורג ירגיש את העומסים

(עם עבור bolt).
לכן המאמצים שהוא יחווה:

קו עומס טיפוסי שבורג חווה מוצג באיור הבא, בו המאמץ מתחיל מהמאמץ להידוק התחלתי וגדל בשיפוע קבוע של , כאשר .

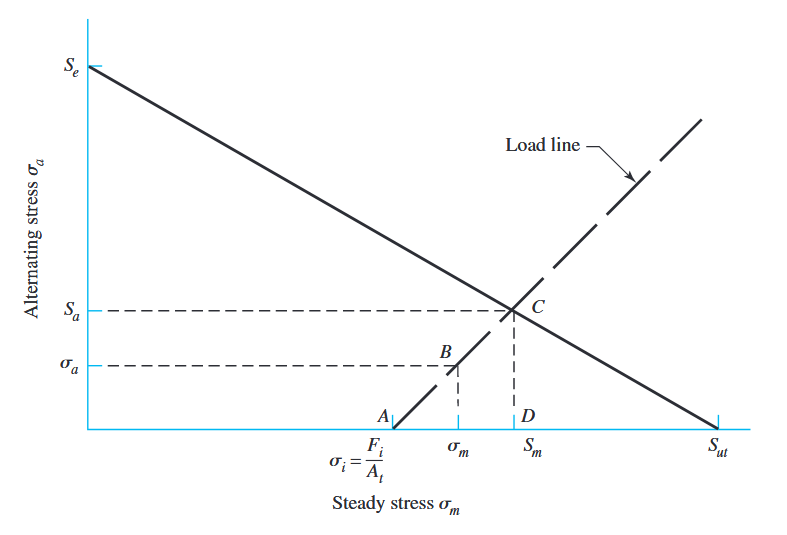
דיאגרמת התעייפות המציגה קו קריטריון גודמן וקו עומס בשימוש נפוץ להידוק התחלתי לעומס תונד. (Budynas et al., 2015).

קו קריטריון גודמן גם כן מוצג באיור לעיל. נוכל למצוא את מקדם הביטחון ע”י חיתוך שני הקווים, כך שנקבל את הנקודה . מקדם הביטחון להתעייפות מוגדר כ:

לאחר מספר חישובים נקבל את הביטוי הבא למקדם ביטחון להתעייפות:

כמקדם ביטחון למחזור ראשון (תאכלס, קריטריון לנגר) נחשב:

הקשר בין מומנט לכוח הידוק בבורג

כעת, אנו יודעים שהידוק התחלתי במחבר בורגי הוא חיוני לתפקוד המחבר. כעת אנו רוצים לוודא שההידוק הרצוי באמת התרחש כאשר אנו מרכיבים את המחבר.
דרך נפוצה היא להשתמש ביָדִית מוֹדֶדֶת פִּתּוּל (torque wrench):

ידית מודדת פיתול Wikipedia.

בידית זו יש מנגנון שיודע להציג את מומנט ההידוק, ובחלקם יודעים גם לעצור ברגע שמגיעים להידוק המתאים.

אנו יודעים לחשב קירוב די טוב למומנט הנדרש כדי ליצור הידוק מסוים. ממשוואות המומנטי הנעה, נקבל כי:

או, עם ביטוי זווית המעלה (קדמה) :

כדי לפשט את המשוואה נהוג להגדיר מקדם מומנט , ולחשב את מקדם זה עבור ברגים סטנדרטיים, כך שניתן לרשום:

ערכי עבור חומרים שונים ניתן למצוא בטבלה 8-15. קירוב גס הוא .

מחברים בורגיים ומסמרות בגזירה

מַסְמֶרֶת היא סוג מחבר המהדק בין שניים, או יותר, מצעים, באופן תמידי.

מסמרות. Wikipedia.

מחברי מסמרת על גשר רכבת. Wikipedia.

אנו מתייחסים למחברים בורגיים ומחברי מסמרת בגזירה באופן זהה לחלוטין. האיור הבא מתאר מחבר העמסות וכשלים של מחבר מסמרת:

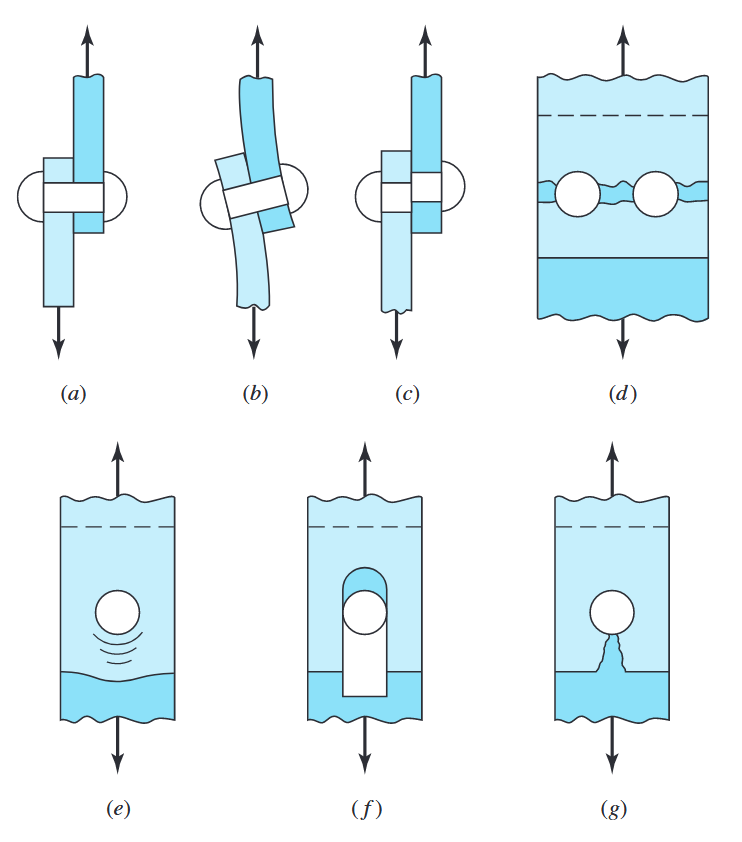
אופני כשל במחבר בורגי או מחבר מסמרת תחת עומס גזירה. (a) עומס גזירה; (b) כיפוף מסמרת; (c) גזירת מסמרת; (d) כשל מתיחה של המצעים; (e) מעיכה של המסמרת על המצעים או מעיכה של המצעים על המסמרת. (f) תלישה בגזירה; (g) תלישה במתיחה. (Budynas et al., 2015).

במקרה (b) המתואר לעיל מתרחש כשל במסמרת ע”י כפיפה. זוהי תופעה מאוד לא רצויה, ומלכתחילה התכן צריך למנוע כפיפה במחבר.

בהנחה ועובי המצעים הוא ו-, המומנט כפיפה שמתפתח במסמרת הוא:

בנוסף, המאמץ הנורמלי במצע המתפתח מהמתיחה והכפיפה ( עבור member):

כאשר הוא שטח החתך של המצע - נזכור גם להחסיר את השטח של החור למסמרות! מחשבים ערך זה עבור כל מצע.
בחומרים פריכים, יש לקחת בחשבון מקדם ריכוז מאמצים באזור הקדח. בהתעייפות (משיך ופריך) יש לקחת בחשבון .
המקדם ביטחון לכפיפה במצע:

כאשר נחשב את מקדם ביטחון זה עבור המצע החלש יותר.

במקרה של גזירה, כפי שמתואר ב-(c), המאמץ המתפתח במסמרת הוא:

כאשר הוא שטח החתך של כל המסמרות במחבר. במידה וישנם מישורי גזירה (אם למשל המחבר מחבר יותר משני מצעים), אז עבור מסמרת אחת:

כאשר הוא הכוח במסמרת אחת. את אנו מחשבים לפי הקוטר הנומינלי של המסמרת, למרות שכאשר ממסמרים את המסמרת בחום היא נוטה להתרחב טיפה. אם המחבר הוא מחבר בורגי, לוקחים את קוטר הקנה באזור הלא מתוברג, כלומר, אנחנו מחמירים (אלא אם כן אנו יודעים שבמישור הגזירה אנו לא באזור המתוברג).

את מקדם הביטחון נחשב לפי פון-מיזס. עבור מאמץ כניעה למסמרת:

במקרה (e) מתוארת מעיכת המחבר. הערכים המדויקים של הכוחות הפועלים על המסמרת לא יודעים, אז נהוג להניח שהמאמצים מפולגים באופן אחיד על שטח המגע של המסמרת עם המצעים:

כאשר הוא הכוח על המסמרת, ו- הוא קוטר המסמרה ו- הוא עובי המצע. מחשבים ערך זה עבור כל מצע.
מבחינת מקדם ביטחון, ניקח את החוזק למעיכה הקטן מבין המסמרת והמצעים:

כאשר נוכל למצוא את ערכים אלו מטבלה 8-4. לכן מקדם הביטחון:

במקרה (f) מתוארת תלישה, שמתרחשת כאשר המחבר הבורגי/מסמרת נמצא קרוב מדי לקצה המצע. בהנחה והמרחק מהקצה הוא , מומלץ לקחת כאשר הוא קוטר המסמרת. המאמץ גזירה במסמרת מתלישה ( עבור tear) משוערכת כ:

כאשר הוא הכוח על המסמרת ו- הוא עובי המצע. מחשבים ערך זה עבור כל מצע.
מבחינת מקדם ביטחון (לפי פון-מיזס):

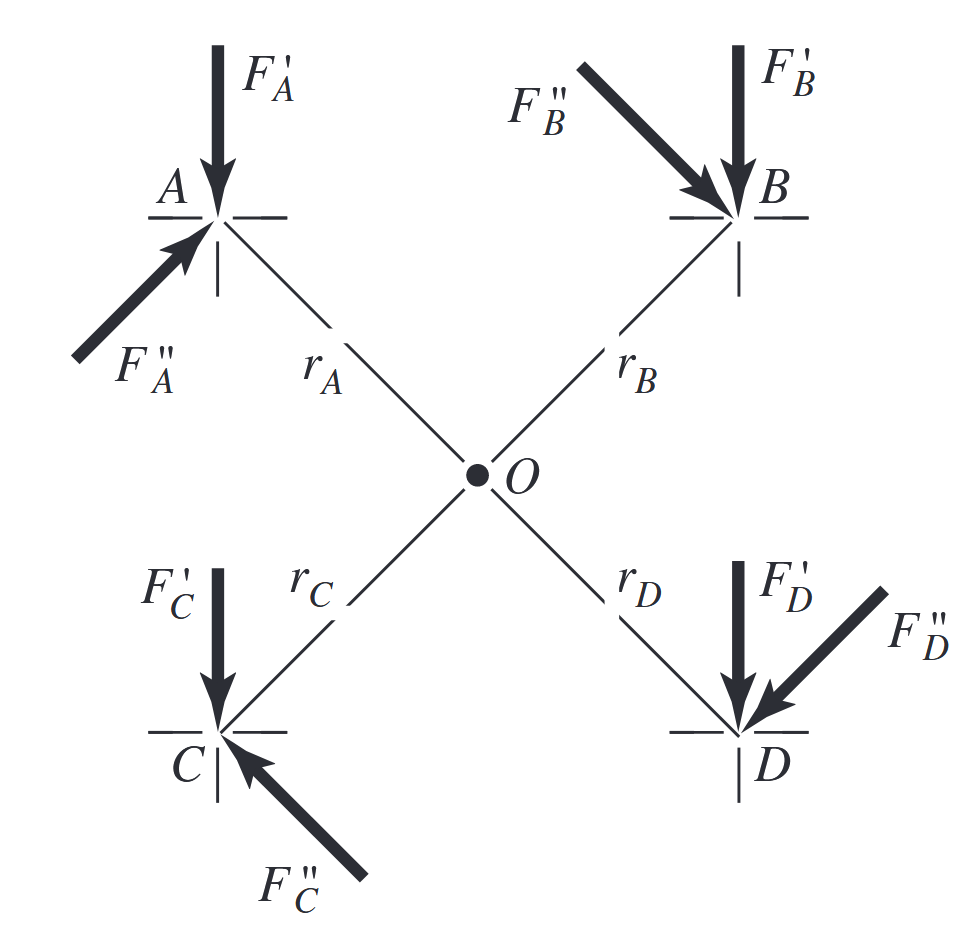
מחברים בורגיים בהעמסה אקסנטרית

במידה והעומס לא פועל על ציר סימטריה של המחברים, אנו קוראים לו העמסה אקסנטרית (eccentric loading). בניתוח מחבר החווה העמסה אקסנטרית אנו מוצאים את מרכז המסה של כל אחד מהמחברים:

כאשר הוא השטח חתך של הבורג/מסמרת/פין ה-.

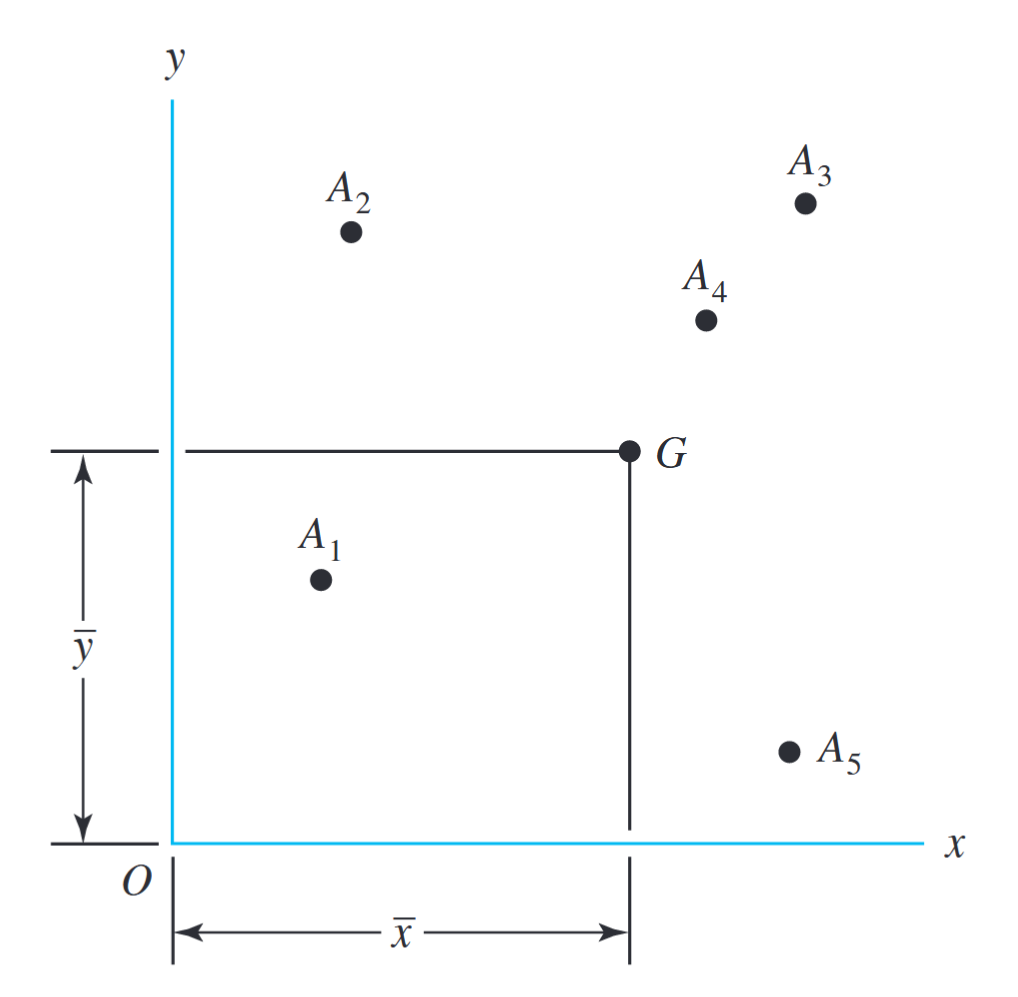
מרכז מסה של פינים, מסמרות, או ברגים.

בהרבה מן המקרים, ניתן למצוא את מרכז המסה פשוט ע”י סימטריה.
דוגמה להעמסה אקסנטרית מוצגת באיור הבא:

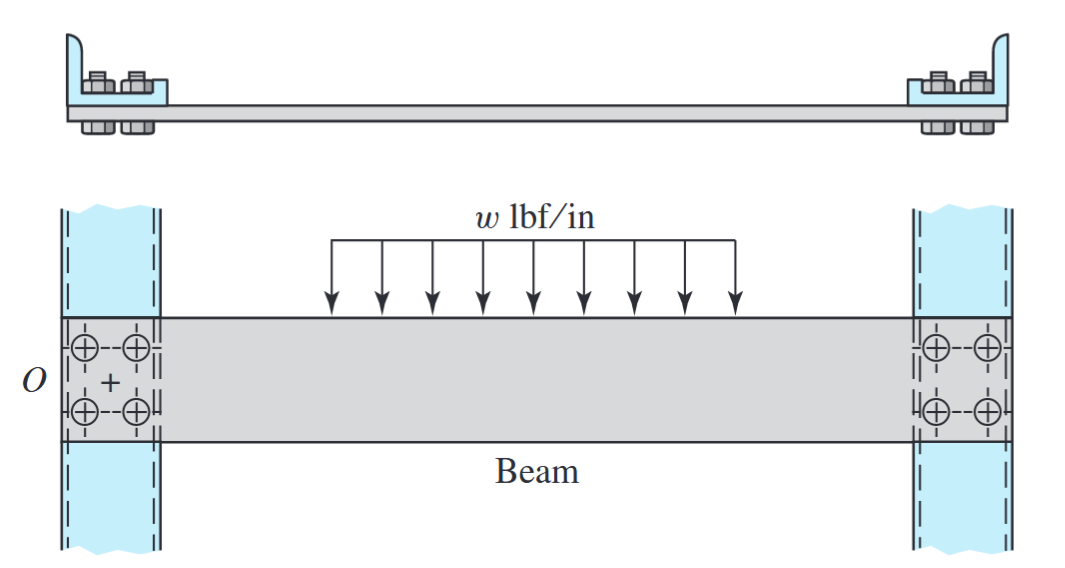
קורה המהודקת משני צדדיה הנתונה לעומס מפורש.

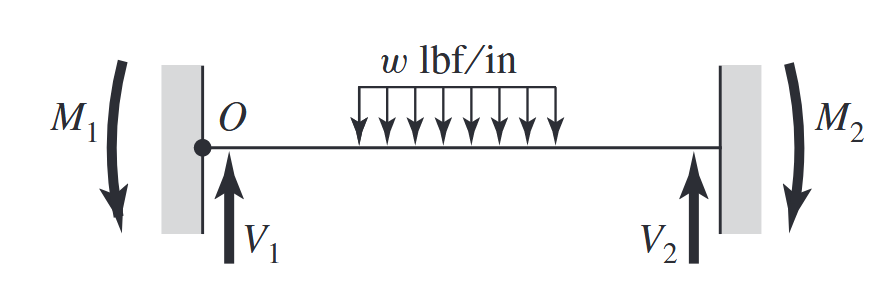
דג”ח על הקורה.

לנוחות, נשרטט ממבט קרוב את קבוצת הברגים.

מבט קרוב על קבוצת הברגים שמרכזה .

נשים לב שבספר הסימונים שונים מהסימונים בקורס:

ל- אנו קוראים כוח הגזירה הראשי, ועבור כוח גזירה חיצוני :

כאשר נשתמש בביטוי הימני אם שטחי החתך במחברים לא זהים, ו:

• המספר הוא מספר המחברים.
• השטח הוא השטח חתך של הבורג .

ל- אנו קוראים או כוח הגזירה המשני, ועבור מומנט פיתול על מרכז המסה :

כאשר נשתמש בביטוי הימני אם שטחי החתך במחברים לא זהים, ולא במרחק שווה ממרכז המסה ו:

• המרחק הוא המרחק של המחבר ה- ממרכז המסה.

מחברים בורגיים בהעמסה בהטיה

עוד מקרה של העמסה אקסנטרית הוא העמסה בהטיה, בו הכוח פועל מחוץ למישור ההידוק. במקרה זה מתפתחים מאמצים גם כתוצאה מכוחות מתיחה ומומנטי כפיפה במחבר:

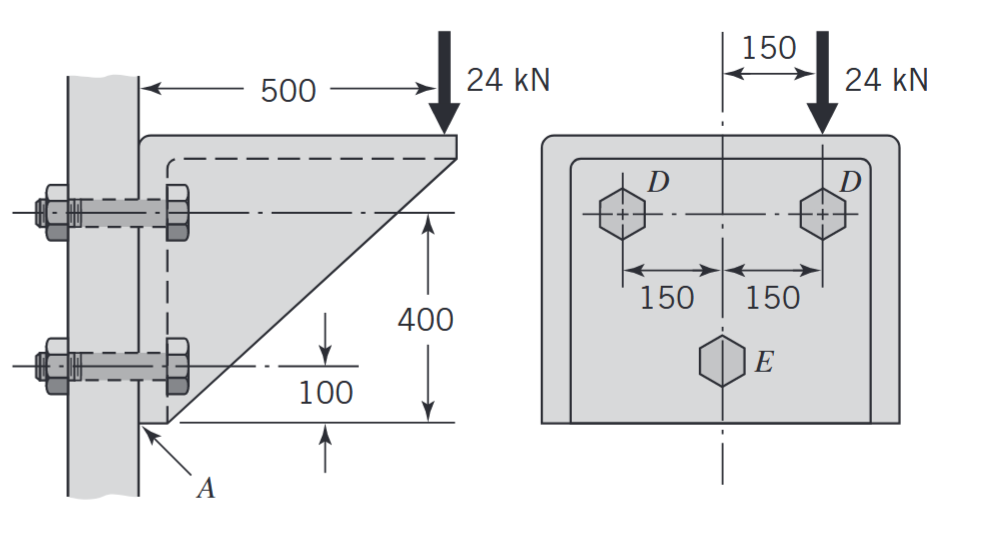
דוגמה להעמסה בהטיה. (Juvinall & Marshek, n.d.).

לעומס כתוצאה מכוח מתיחה חיצוני אנו קוראים עומס המתיחה הישיר , והוא מקיים:

כאשר נשתמש בביטוי הימני אם קשיחויות המחברים לא זהים, ו:

• המספר הוא מספר המחברים.
• הכוח הוא כוח המתיחה החיצוני.
• הקשיחות היא קשיחות המחבר, שהיא בעצם חיבור במקביל של הבורג והמצעים, ולכן .

לעומס כתוצאה ממומנט ההטיה במרכז המסה אנו קראים עומס מתיחה משני , והוא מקיים:

כאשר נשתמש בביטוי הימני אם קשיחויות המחברים לא זהים. בנוסף:

• המרחק הוא המרחק של של הבורג ה- ממיקום ציר ההטיה, כאשר מיקום זה צריך להיות נתון.

תרגילים

תרגיל 1

המתקן המתואר מיועד לשאת משא מקסימאלי של בטווח הגבהים של . הרמה מן הגובה המינימאלי לגובה המקסימאלי תיעשה ע”י לא יותר מ- סיבובים של הבורג. מומנט סיבוב ראש הבורג המקסימאלי יהיה . ניתן להניח כי קוטר הכתף (הצווארון) הינו פי מהקוטר הממוצע של הבורג. מקדם החיכוך הינו . לבורג התחלה אחת. הבורג בעל תבריג ריבועי.

סכמת הבעיה.

העזרו בטבלה הבאה:

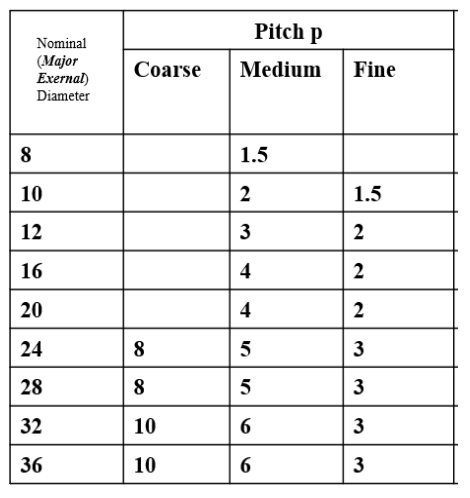
מידות אופייניות לברגי הנעה ריבועיים.

סעיף א’

מה צריך להיות מאמץ הכניעה המינימאלי של חומר הבורג כך שמקדם הביטחון למאמצים בקנה הבורג יהיה ?

פתרון:
עלינו לתכנן בורג שיתאים לדרישות הפונקציונאליות, והבטיחותיות (). לשם כך עלינו לבחור:

• אורך
• פסיעה/קדמת (מעלה) הבורג. במקרה שלנו יש התחלה אחת ולכן הפסיעה והקדמה זהים.
• קוטר
• חומר גלם

חישוב הקדמה:
את הקדמה נחשב ע”פ מספר הסיבובים הדרוש ע”מ להרים את המטען מהגובה המינימלי לגובה המקסימאלי. נחלץ מתוך הנתון על גובה המטען את האורך המקסימלי והמינימלי של ההברגה:

גאומטריית התבריג והזרועות.

נשים לב שמנתוני השאלה .
לכן:

הדרישה בשאלה להרים את המטען מגובה מינימלי לגובה מקסימלי תוך מקסימום סיבובים של הבורג ולכן:

נבח קדמה עגולה ע”פ תקן:

חישוב הקוטר הראשי:
מחיכוך בצווארון, מומנט ההנעה הוא:

נתון כי ו-. נחשב את מדג”ח:

דג”ח על המשא העליון.

מהדג”ח, מאחר ואנו מניחים שיווי משקל, נקבל:

דג”ח על הבורג.

לכן:

הכוח המקסימלי כאשר הזווית מינימלית ולכן:

נציב בחזרה בביטוי לכוח ההנעה , עם הדרישה שהוא לא יעלה על :

נציב נתונים ונגיע למסקנה ש:

נבחר קוטר פסיעה כך ש- יהיה עגול וע”פ תקן. אנו יודעים ש- (ע”פ תקן) ולכן מהתנאי על :

לפי הטבלה הנתונה, נבחר , מה שאומר ש:

חישוב מאמצים בקנה*:
נצטרך כעת למצוא את . מהצבה של נתוני הבורג שבחרנו נקבל ש:

נחשב מאמצים בקנה הבורג:

לכן המאמץ המקסימלי השקול (לפי פון-מיזס):

לכן חוזק הבורג בקנה עבור מקדם ביטחון :

סעיף ב’

האם המתקן בעל נעילה עצמית?

פתרון:
נבדוק את המומנט הנעה להנמכת עומס של המתקן (יש גם חיכוך עם הצווארון, כך שנצטרך לבדוק את במקום להציב בתנאי לנעילה עצמית):

נציב נתונים ונקבל כי:

קיבלנו שמומנט הורדת העומס חיובי ולכן המתקן הוא בעל נעילה עצמית.

תרגיל 2

באיור מתואר מיכל לחץ. המיכל כולל מכסה (1), גוף (2), אטם (3), 10 בורגי הידוק בדרגת חוזק (4), ואומים (5). הברגים בעלי אורך ועשויים פלדה .

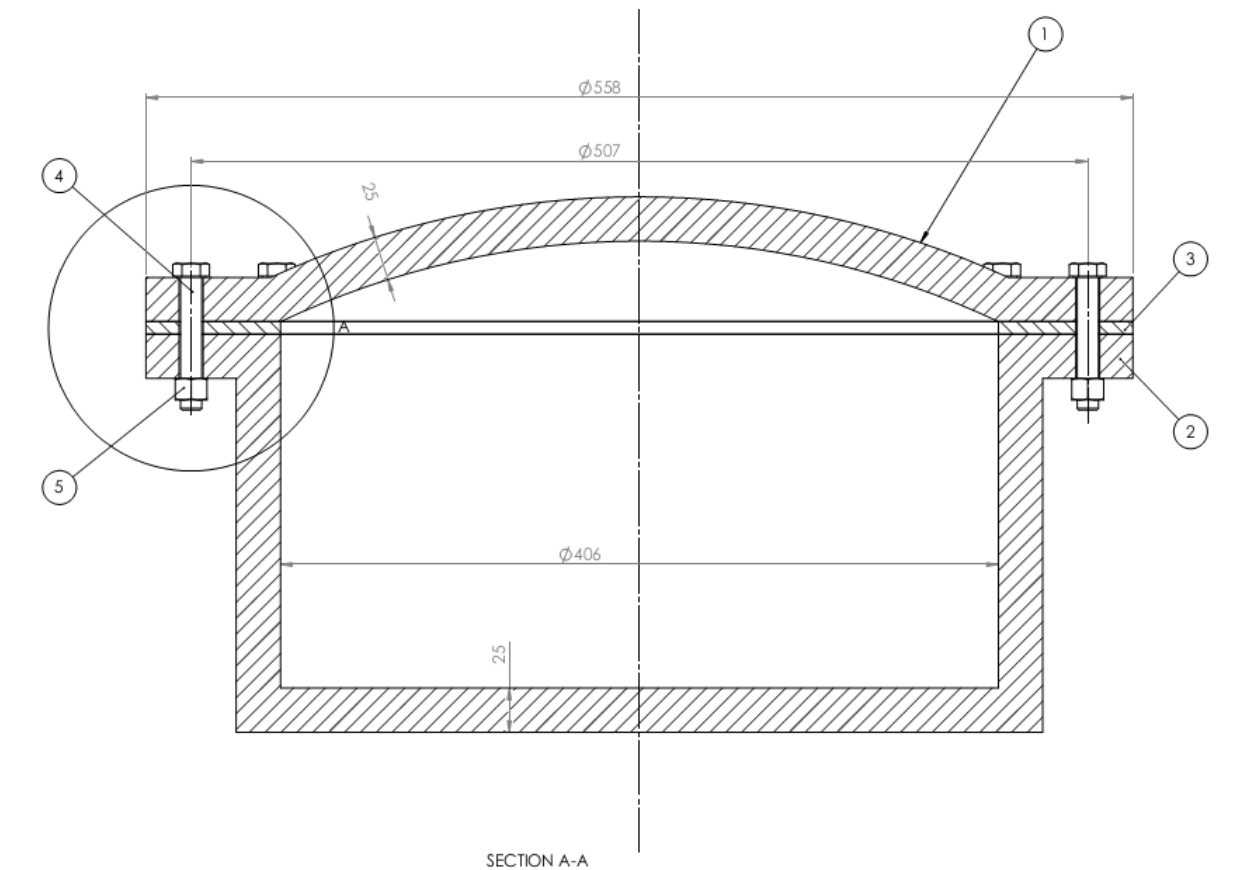
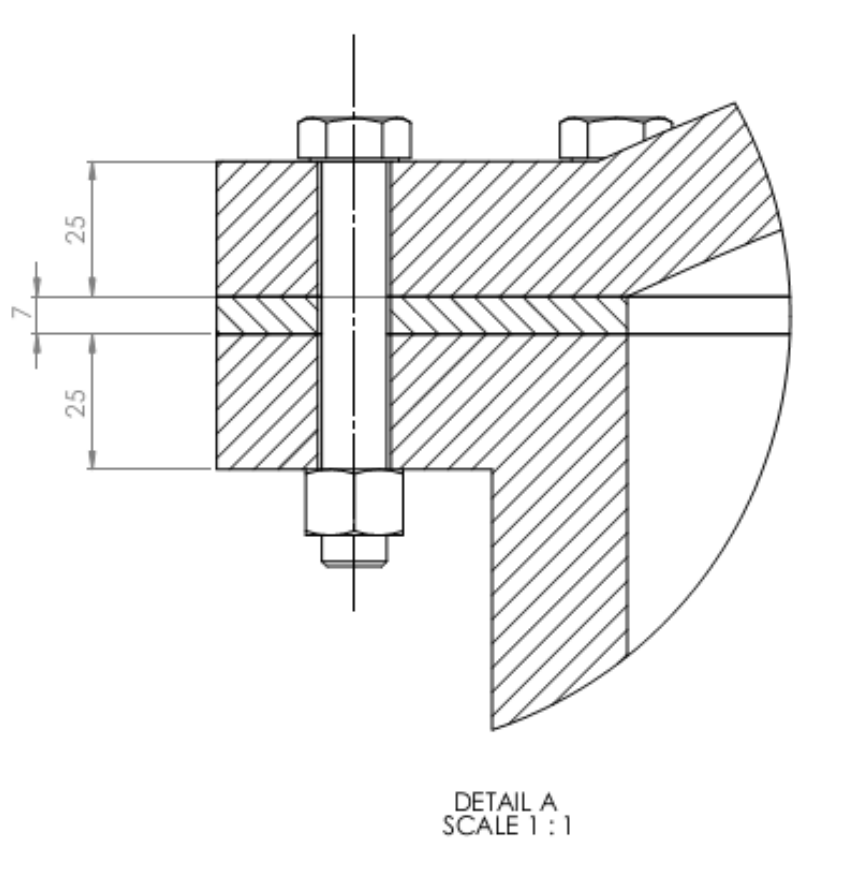
סכמת הבעיה.

מכסה המיכל עשוי ברזל יציקה בעל מודול אלסטיות , גוף המיכל עשוי פלדה בעלת מודול אלסטיות , והאטם עשוי נחושת בעל מודול אלסטיות . כוח ההידוק ההתחלתי בברגים . המיכל מלא אוויר בטמפרטורה בלחץ אטמוספרי.

לחץ האוויר במיכל עולה ל-. חשב את העומס המתפתח בכל אחד מהברגים ואת מקדם הביטחון כנגד כשל החיבור.

פתרון:
נתחיל מקשיחות הבורג:

מהנתונים והשרטוט:

לכן, לפי משוואה (SH8-14):

בנוסף:

הברגים הם , ולכן לפי MDN1_C8 טבלאות ברגים:

כמו כן:

נציב הכל בקשיחות הבורג:

נעבור כעת לקשיחות מצע החיבור.

גאומטריית פילוג המאמצים במצעים.

לפי (SH8-20), קשיחות המצע העליון (המכסה), עם :

באותו אופן, עבור האטם נחושת, עם :

ועבור גוף המיכל:

נחבר את הקשיחויות בטור:

לכן מקדם הקשיחות הוא:

העומס החיצוני על כל בורג הוא:

כאשר הוא השטח שהלחץ פועל עליו, הוא הלחץ במיכל, ו- מספר הברגים. מאחר ויש 10 ברגים:

העומס המתפתח בכל אחד מהברגים, לפי משוואה (SH8-24), עם הנתון כי :

מקדם הביטחון לכשל הבורג:

בדרגת חוזק , לפי טבלה 8-11:

ולכן:

לפי משוואה (SH8-30), מקדם הביטחון כנגד ניתוק:

ניקח את המינימלי מבין המקדמי ביטחון:

תרגיל 3

באיור הבא מוצג אזור המכסה של מיכל לחץ אוויר דחוס המסק אוויר למערכת פניאומטית ונטען ע”י מדחס. הלחץ במיכל נע בין לחץ מרבי של ולחץ מזערי של .

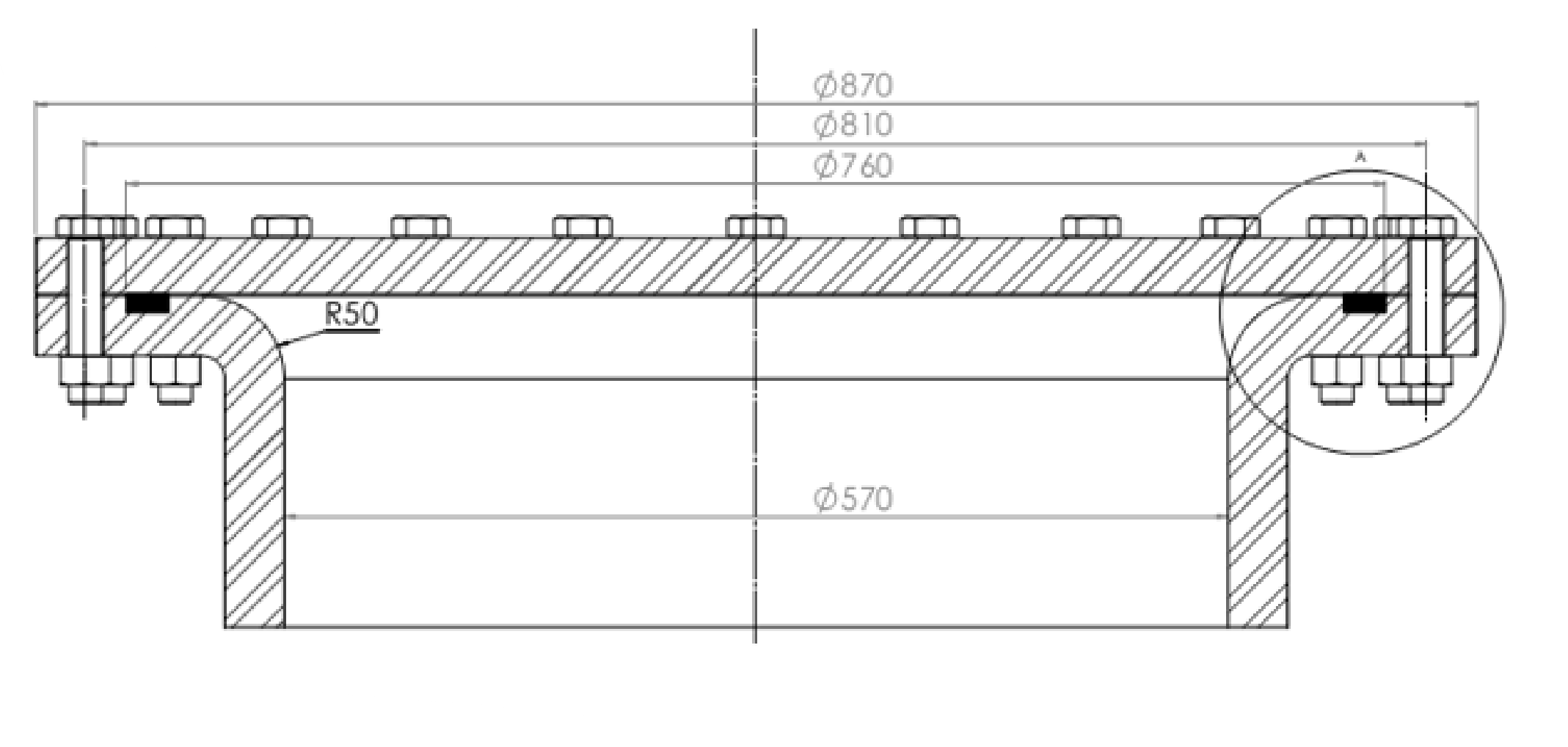
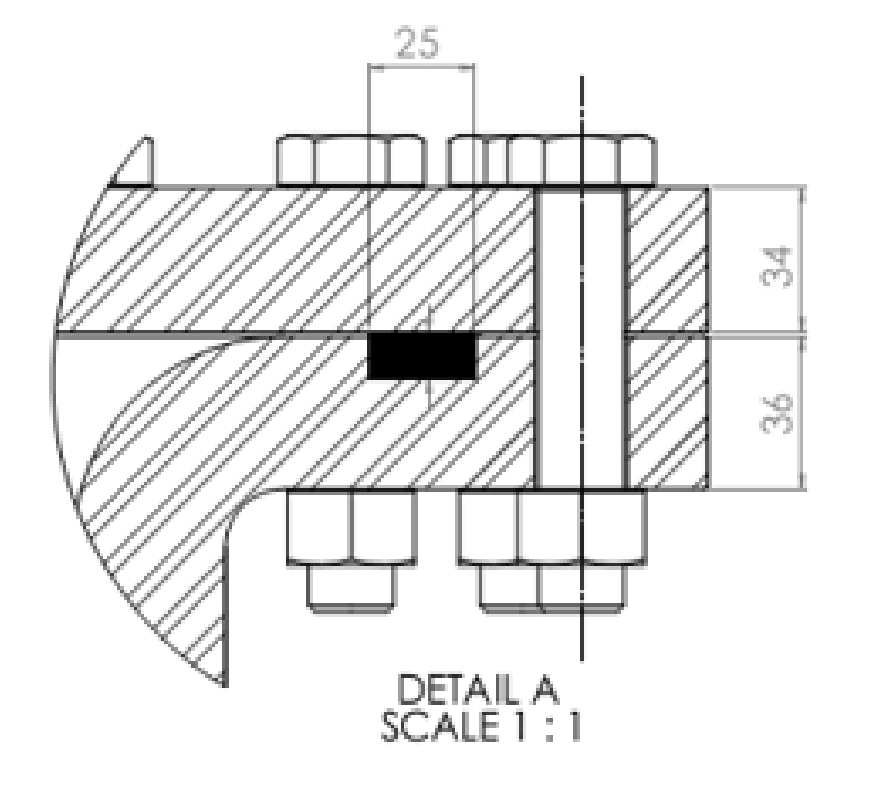
סכמת המכסה לחץ אוויר דחוס.

האטימות מושגת באמצעות אטם תחום העשוי מתכת ו-PTFE. המכסה מהודק באמצעות 24 ברגים מטריים () בדרגת חוזק עשויים בשיטת rolled threads.
המיכל, המכסה והברגים עשויים מפלדה. אורך הברגים .

קריטריונים לתכן:

1. כדרישת בטיחות יש לוודא כי במקרה של חוסר הידוק הברגים (אין הידוק ראשוני ) הברגים לא יכשלו במקדם ביטחון של .
2. מידות האטם נקבעו כך שעבור אטימה תקינה נדרש לוודא כי מאמץ הלחיצה בין המצעים לא יהיה נמוך מ-.

סעיף א’

קבעו את קוטר הברגים לעמידה בדרישת הבטיחות בעומס מירבי (ללא התעייפות).

פתרון:
הלחץ במיכל מפעיל כוח כלפי מעלה - הוא מנסה לפתוח את המכסה. השטח שהוא פועל עליו הוא השטח עד האטם, כי האוויר לא עובר את האטם.

מבחינת הדרישה הראשונה, אנו רוצים שכאשר , אז מקדם הביטחון עבור הברגים יהיה . מאחר ואין הידוק, אין עומס על המצעים (), ולכן כל העומס ייפול על הברגים.

נמצא את הכוח המקסימאלי הפועל על הברגים (כאשר ניקח את המקרה קיצון של ):

כאשר סמנו לב להחסיר את קוטרי האטמים משני הצדדים.
לכן הכוח המקסימאלי על בורג יחיד:

כיוון ש- , אז לפי טבלה 8-11:

לפי מקדם ביטחון לחוזק מוכח (כאשר במקרה שלנו ):

נעביר אגפים:

זהו השטח האפקטיבי המינימאלי.
נציב נתונים:

מטבלה 8-1, הבורג (עבורו ) הוא הבורג בעל הקוטר הקטן ביותר העומד בדרישה ולכן נבחר אותו.

סעיף ב’

השתמש בברגים שבחרת וחשב את כוח ההידוק הראשוני () בכדי להבטיח אטימות בכל מתאר הפעולה של המיכל.

פתרון:
מבחינת הדרישה השנייה, כאשר יש אטימה, אנו דורשים ש- . נתייחס כאן לשטח המגע בין המתכות של המכסה והאוגן (ללא האטם וללא הברגים).
תנאי זה נדרש להתקיים בלחץ הפנימי המרבי במיכל ().

נמצא את הכוח על המצעים הנדרש כדי להבטיח לחץ זה על האטם (לפי לחץ באטם):

לכן עבור בורג אחד:

כעת נמצא את יחס הקשיחויות.

• קשיחות הבורג:

  עבור הבורג שבחרנו, , ומהנתונים:

  נציב בביטוי לקשיחות הבורג:

• קשיחות מצע החיבור:
  מאחר והמכסה והמיכל עשויים פלדה, נשתמש בקירוב גרין:

  מ8-8 נקבל את הקבועים הדרושים, ונמצא כי:

לכן קבוע המחבר:

נמצא את הכוח שהלחץ מפעיל על הברגים ( הוא הכוח החיצוני עבור בורג יחיד):

לכן כוח ההידוק הראשוני הדרוש:

ולכן:

סעיף ג’

חשב את מקדם הביטחון של הברגים כנגד כשל בהתעייפות לאורך חיים אינסופי באמינות של .

פתרון:
נמצא את אמפליטודת המאמץ והמאמץ הממוצע הפועל על כל בורג (לפי התעייפות מחבר בורגי). נצטרך קודם למצוא את הכוח המינימלי והמקסימלי הפועל על כל בורג:

נשים לב מטבלה 8-16 ש- , ולכן (לפי משוואות (SH8-35) ו-(SH8-36)):

נחשב את גבול ההתעייפות לאורך חיים אינסופי באמינות של , לפי משוואת מארין:

ולכן:

נחשב מקדם ביטחון לפי קריטריון גודמן (אבל עם התחשבות בהידוק ההתחלתי):

וכמובן כמובן כמובן שגם נחשב את מקדם הביטחון לפי לנגר:

תרגיל 4

באיור מתוארת קורת פלדה מלבנית המחוברת אל שתי לוחות פלדה. במרכז הקורה מופעל כוח של . הקורה מחוברת של הלוחות באמצעות ברגים המתפקדים כמסמרות.

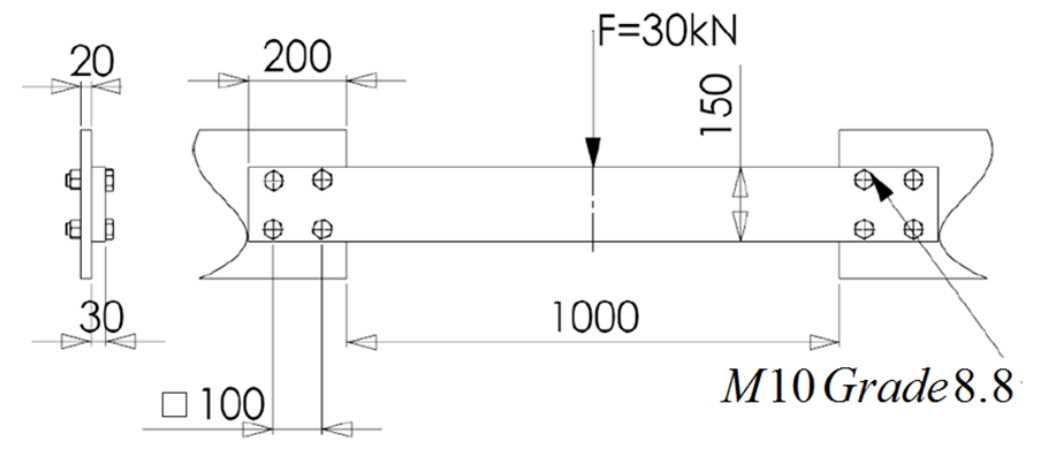
חשב את מקדם הביטחון לכשל הבורג.

פתרון:
כשלב ראשון נמצא את הכוחות והמומנטים הפועלים על כל אחד מהחיבורים. נדמה כל אחד מהם לריתום שנמצא במרכז הכובד של החיבור.

דג”ח חיצוני על הבעיה.

זוהי בעיה לא מסוימת סטטית שנצטרך להשתמש בה בשיקולי סימטריה ודפורמציה, אבל אנחנו בתכן, ולא במוצקים, ולכן ייתנו לנו תמיד טבלה רלוונטית:

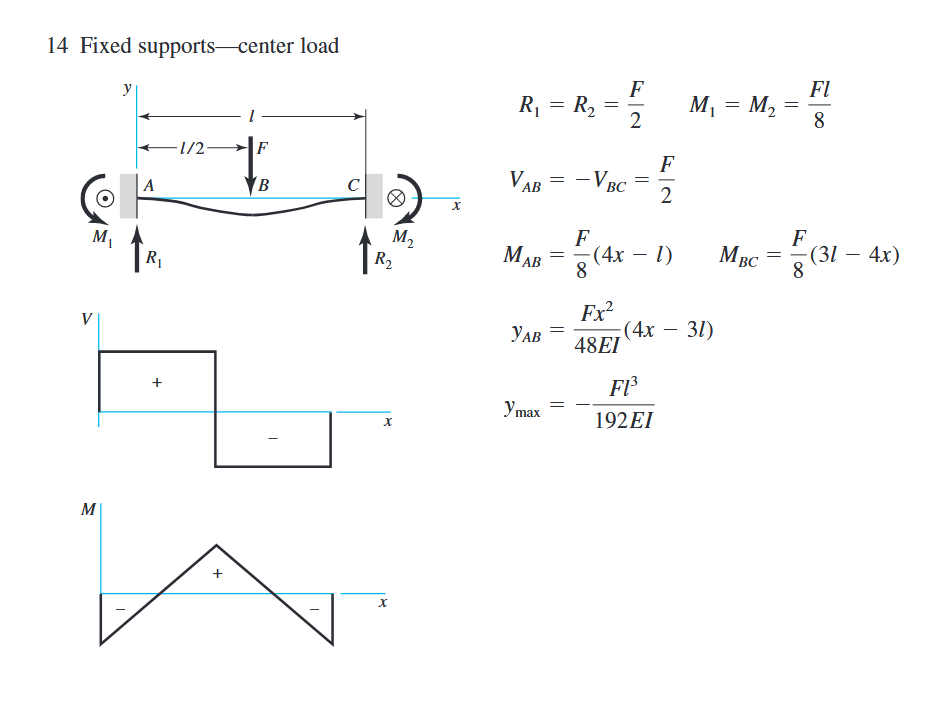
טבלת שקיעות שרלוונטית לבעיה שלנו. (Budynas et al., 2015).

נקבל כי:

כעת עבור כל ריתום, נחשב את הכוחות הפועלים בכל מסמרה:

דג”ח כל הריתום.

נשים לב שהמסמרות הכי מסוכנות הן מסמרות 2 ו-4, אז נחשב את הכוחות עבור אחת מהן:

לכן גודל הכוח:

שרטוט להמחשת חישוב גודל הכוח, כי שכחתי לרגע איך מחשבים גודל של חיבור וקטורי.

באיור לא מוגדר האם הגזירה של משטחים באזור המתוברג או לא. לכן נחשב את מקדם הביטחון לחומרה, וניקח בחשבון את האזור המתוברג.
לפי טבלה 8-1, עבור :

לפי טבלה 8-11:

נמצא את מאמץ הגזירה בבורג ואת מקדם הביטחון:

ולכן לפי פון מיזס:

→ קודם: MDN1_002הבא: MDN1_004 ←