SLD1_007 מאמץ ועיבור

→ קודם: SLD1_006הבא: SLD1_008 ←

מאמץ ועיבור

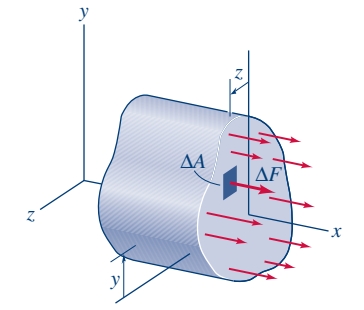
נביט בקורה הבאה:

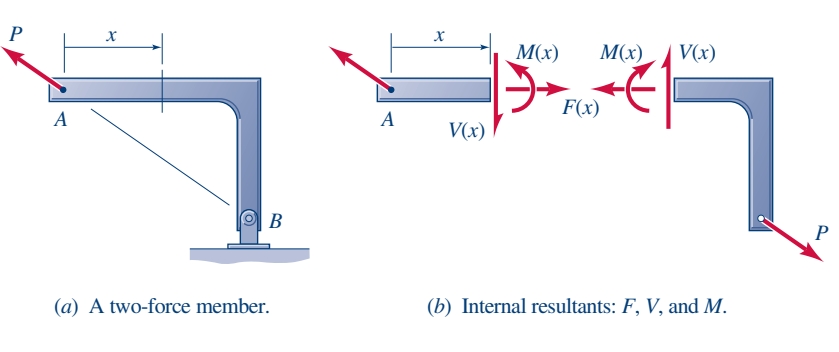
הכוחות הפנימיים לא מספיקים כדי לתאר לנו את הכוחות המפורסים המסובכים הפנימיים שפועלים בתוך הקורה. מושג המאמץ יעזור לנו לתת משמעות לכוחות אילו.

צורת הקורה באיור יכולה להשתנות כתוצאה מהכוח . מושג העיבור ייתן לנו לתאר במדויק דפורמציה מסוג זה.

דפורמציה

דפורמציה היא השינוי בגודל או הצורה של גוף מסוים. דפורמציה יכולה להתרחש כתוצאה מעומסים חיצוניים, פעולות פנימיות, שינויים בטמפרטורה ועוד. עיבור/עיוות הוא השינוי היחסי של גוף מסוים, ואנו נעסוק בעיבור של גוף תחת מאמץ מסוים.

מאמץ

נתחיל בדוגמה פשוט של מוט תחת עומס חד-צירי:

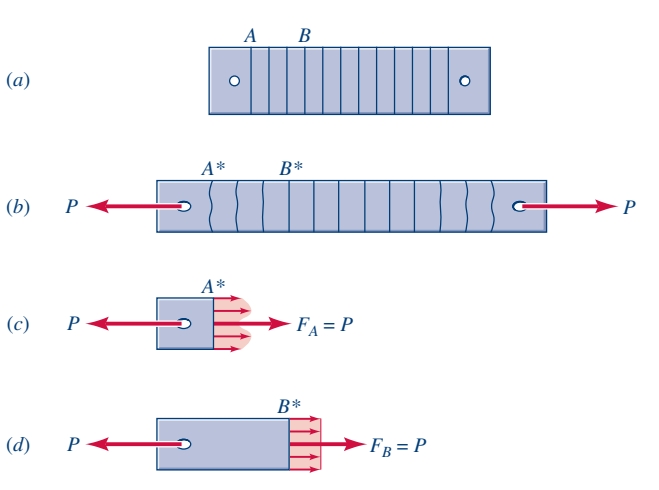
בקצוות המוט, למשל בחתך , הכוח הנורמל המפורס לא אחיד לאורך החתך. אבל בחתך , הרחק מהנקודה בה מפעילים את הכוח, הכוח המפורס אחיד. מאמץ הוא החילוק של הכוח לשטח מסוים - והוא מתואר ככוח ליחידת שטח:

מאמץ נורמל

אנו נעסוק במאמץ הנורמל, אך נשים לב כי גם לכוח הגזירה יש כמובן מאמץ המוגדר לו. מאמץ הנורמל מוגדר באופן הבא:

או מתמטית:

הגדרה:

מאמץ הנורמל בנקודה עבור כוח נורמל הפועל על שטח מוגדר באופן הבא:

כאשר מידותיו:

מבחינת סימן המאמץ, כמו במתיחה ולחיצה, סימן חיובי של מעיד על מתיחה, וסימן שלילי של מעיד על לחיצה.

המאמץ הממוצע על חתך בעל שטח :

שקול מאמץ נורמל

כמו בעומס מפורס, גודלו ומיקומו של שקול המאמץ הנורמל (לפי מרכז מסה):

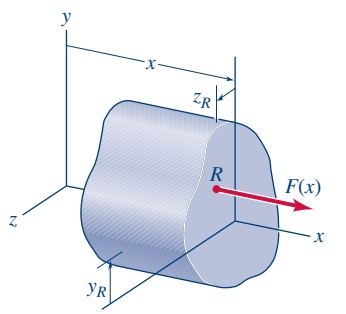
מאמץ צירי

בהנחה ומאמץ הנורמל קבוע לאורך כל החתך, נקרא לו מאמץ צירי, ונוכל להסיק כי:

כאשר הוא הכוח בחתך , ו- הוא השטח בחתך .

עיבור

כאשר גוף נתון תחת עומס חיצוני או שינוי טמפרטורה, הוא עובר דפורמציה - שינוי בגודל או צורת הגוף:

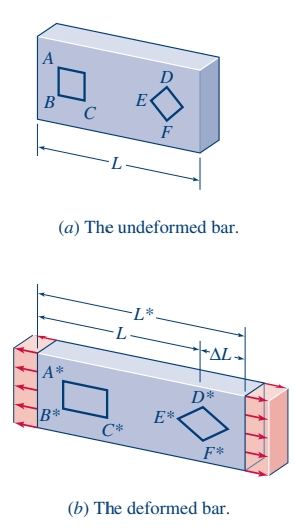
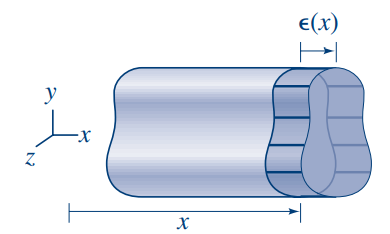
כדי לתאר כיצד המתיחה משפיעה באופן מקומי על המוט, שני ריבועים משורטטים באיור. שינויים מקומיים באורך, כפי שמוצג בקטע , כאשר הוא נמתח הוא הופך לקטע , והוא מתואר ע”י המושג עיבור נורמל. שינויים מקומיים בזוויות, כפי שמוצג בזווית הישרה , כאשר הוא נמתח הוא הופך לזווית , והוא מתואר ע”י המוגש עיבור גזירה, שלא נעסוק איתו.

עיבור נורמל

נביט באיור הקודם.

הגדרה:

עיבור נורמל המומצע מוגדר כהיחס בין ההתארכות הכללית לאורך המקורי :

מאחר ועיבור הוא יחס, הוא חסר יחידות.

בהמשך נניח כי העיבור הוא אחיד לאורך המוט. סוג זה של עיבור אחיד נקרא עיבור צירי ובמקרה זה:

עיבור תרמי

נעסוק כעת בקשר בין הטמפרטורה של גוף לעיבור נורמל שלו. רוב החומרים, כאשר הם נתונים תחת חימום אחיד, מתרחבים בכל הכיוונים, באופן הבא:

הגדרה:

עיבור תרמי נתון ע”י:

כאשר הוא העיבור התרמי, הוא מקדם ההתרחבות התרמית, ו- הוא השינוי בטמפרטורה.

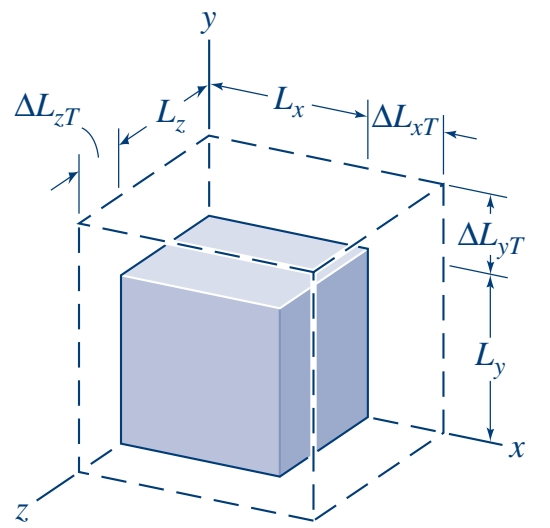
מאחר והעיבור מתרחש בכל הכיוונים, אנו יכולים לחשב את ההתארכות הכללית של הגוף:

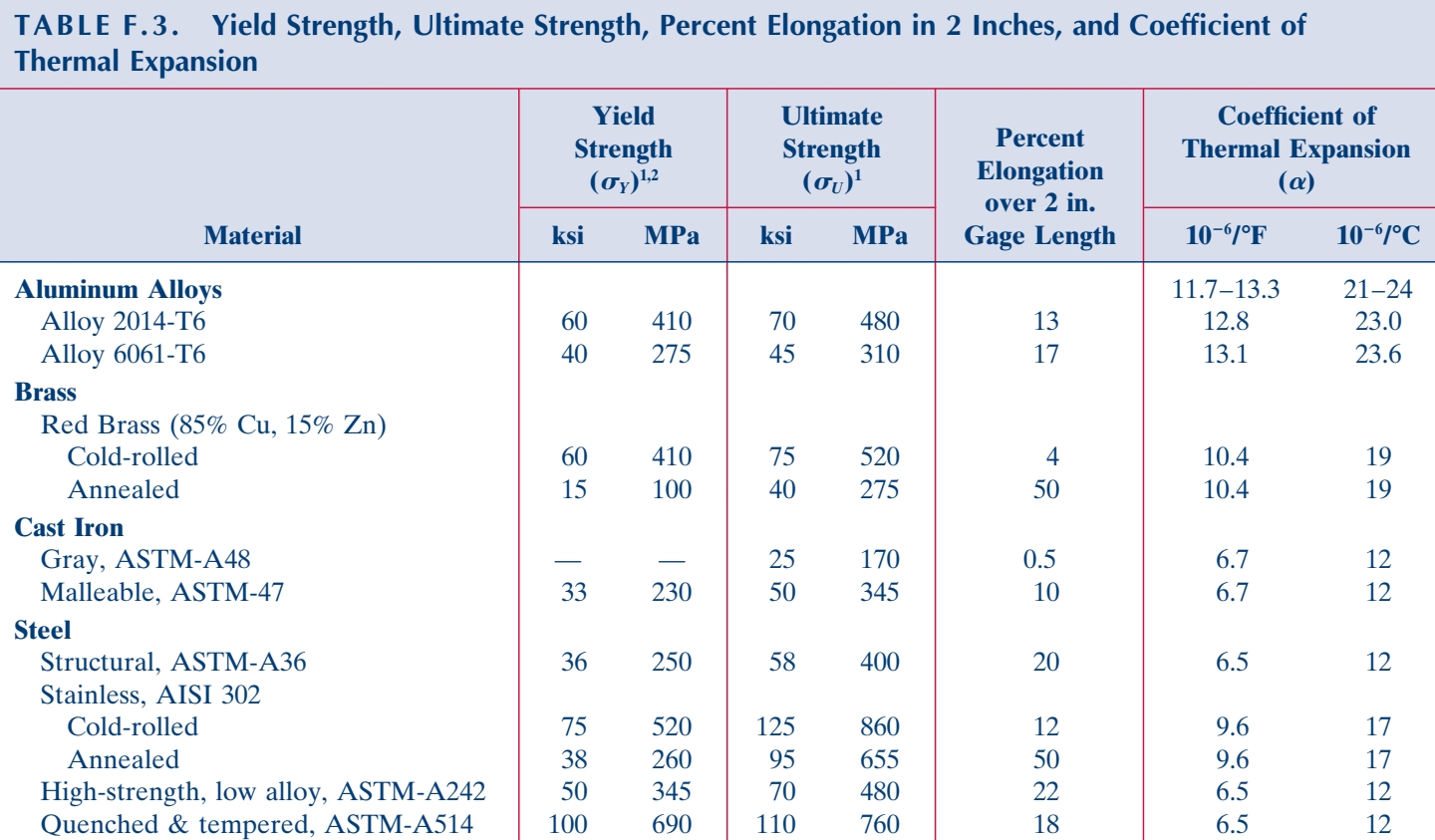
דיאגרמות מאמץ-עיבור

כדי לקשר בין העומס על מבנה מסוים לדפורמציה הנוצרת כתוצאה מהעומס, עלינו לבצע ניסויים על המבנה כדי לאפיין את הקשר מאמץ-עיבור.
ניסוי נפוץ למציאת הקשר הוא בעזרת ניסוי מתיחה/לחיצה על חומרים שונים:

מוט תחת מתיחה ע”י כוחות נמדד באורכו לפני ואחרי המתיחה:

גרף של המאמץ מול עיבור נקרא דירגרמת מאמץ-עיבור, ומדיאגרמות אלו אנו יכולים להסיק מספר מסקנות על התכונות המכניות של החומר. הערכים איתם אנו בונים את הדיאגרמה הם מאמץ הנדסי (עומס חלקי שטח החתך ההתחלתי) ועיבור הנדסי (התארכות חלקי האורך ההתחלתי של המוט):

תכונות מכניות של חומרים

נתונה דיאגרמת מאמץ-עיבור של פלדה:

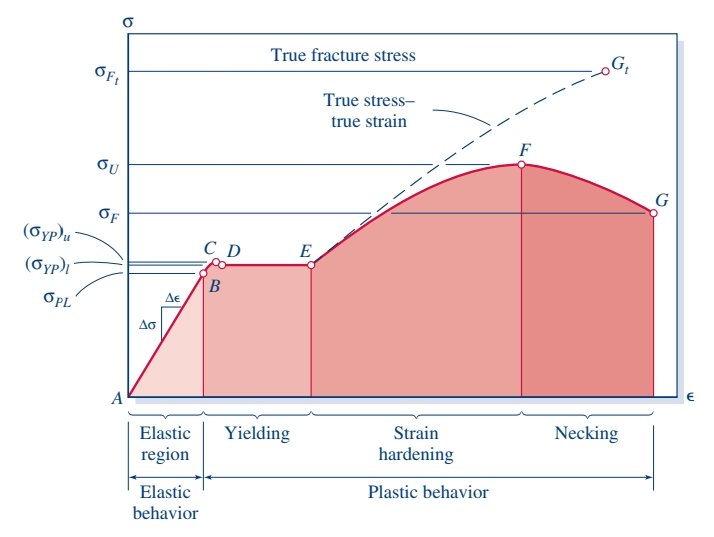
מודול יאנג

מהנקודה לנקודה ישנו קשר לינארי בין המאמץ והעיבור. המאמץ בנקודה נקרא גבול הפרופורציונאליות יחס זה נקרא מודול יאנג, והוא נתון ע”י:

היחידות של הן ב-. לחומרים בהן נעסוק הן לרוב יהיו בסדרי גודל של ().

הקטע נקרא אזור אלסטי - לאחר שנשחרר את החומר מהמאמץ בנקודה על , הוא יחזור בחזרה לצורתו המקורית.

נקודת כניעה

אחרי הנקודה , החומר מתחיל להיכנע, כלומר, תוספות קטנות יותר של עומס דרושות כדי ליצור התארכות מסוימת. לאחר נקודה זו, אנו כבר באזור הפלסטי - לאחר שחרורו של החומר מן המאמץ, הוא ינסה לחזור לצורתו המקורית, אך לא יעשה זאת בצורה מושלמת.

המאמץ בנקודה נקרא נקודת כניעה . מ- ל-, החומר ממשיך להתארך בלי שום שינוי במאמץ. המאמץ חוזר לעלייה בנקודה , עד הנקודה שנקראת Ultimate Strength (UTS).

בנקודה , המאמץ מתחיל לקטון, וצוואר המוט נהיה דק יותר, עד הנקודה - נקודת השבר.

תיאור מוחשי:

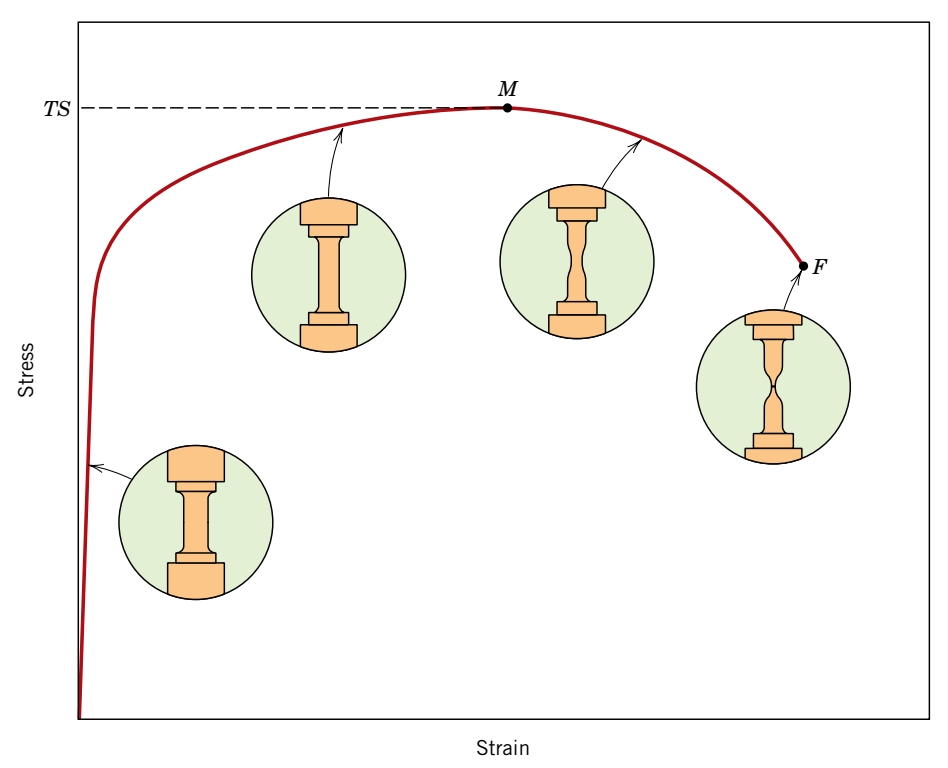
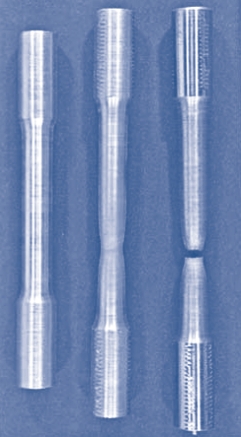
מאמץ ועיבור אמיתיים

המאמץ האמיתי, , הוא המאמץ ברגע מסוים במהלך הבדיקה, חלקי שטח החתך באותו הרגע, לעומת מאמץ הנדסי בו השתמשנו בשטח החתך ההתחלתי. לכן, ברגע בו צוואר המוט נהיה דק יותר, שטח החתך מתחיל להשתנות, ואז למאמץ האמיתי והמאמץ ההנדסי ישנם ערכים שונים.
העיבור האמיתי, , הוא השינוי הרגעי באורך המוט חלקי האורך של המוט באותו הרגע.
שני ערכים אלו נתונים ע”י הנוסחאות:

נוסחה:

בתחום הפלסטי היציב (עד ה-UTS בהנחת שימור נפח), לפני היווצרות הצוואר מתקיים:

נוסחה:

ניתן לחשב עיבור אמיתי גם ע”י שינוי בשטח:

נוסחה:

בגרף הראשון, משורטט בקו מקווקו המאמץ האמיתי מול העיבור האמיתי.

דפורמציה צירית

דפורמציה חד-צירית מאופיינת ע”י שתי הנחות:

1. הציר של המוט נשאר ישר.
2. החתכים המישוריים שמאונכים לציר, נשארים מישוריים ומאונכים לציר לאחר הדפורמציה, והם לא מסתובבים סביבו.

משוואת עיבור-העתק

הנחות אלו מתוארות באיור הבא:

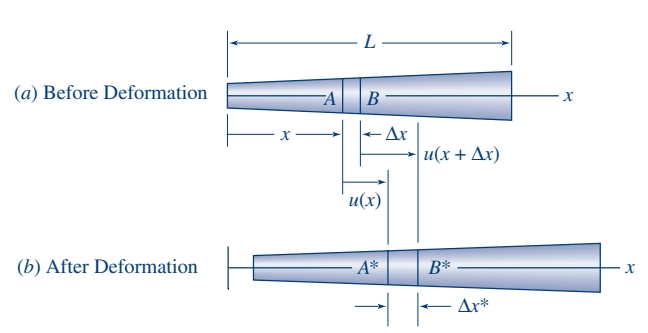
הנקודות ו- הן חתכים במקום ה-, ובמקום ה- בהתאמה, לפני הדפורמציה. ו- הם אותם חתכים, אחרי הדפורמציה.

ההעתק (שינוי במיקום) של מסומן ב-, ואלו ההעתק של הוא . אנו יכולים לבנות ביטוי עיבור-העתק המקשר בין העיבור להעתק כאשר נזכור כי עבור עיבור צירי:

העיבור הצירי של כל סיב (שורה של חלקיקים) בעל אורך אינפיטסימלי שמקביל לציר ה- ומתחיל בחתך ומסתיים בנקודה ניתן לחישוב ע”י ההגדרה של עיבור צירי בנקודה. בהנחה ואורך הסיב הוא , ונתחיל להשאיף את זה לאפס, אנו יכולים לכתוב את הביטוי הבא לעיבור הצירי:

לכן:

משפט:

העיבור הצירי בחתך הוא הנגזרת (לפי ) של ההעתק הצירי:

משוואת התארכות

נביט באיור הבא:

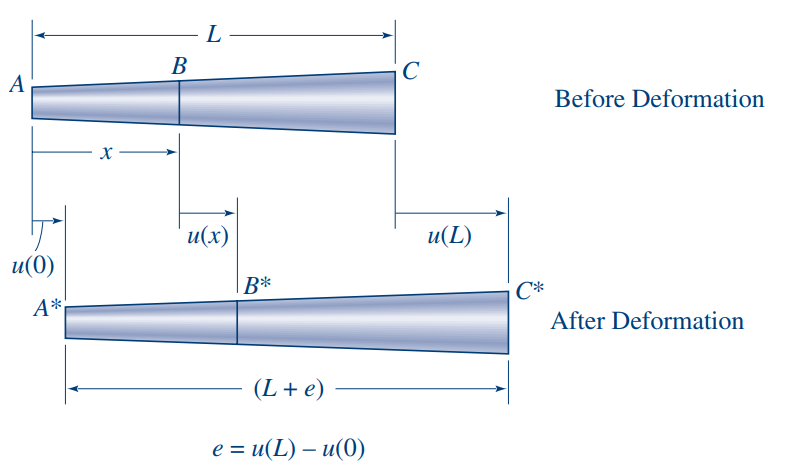
ההתארכות הכללית היא פשוט ההפרש בין ההעתקים של שתי הקצוות:

מה הקשר ?

זה רק סימון של הספר - אין קשר לקבוע .

ע”י סכימה של כל השינויים באורך,כתלות בתוספות אינפיטסימליות לאורך כל המוט, אנו מקבלים את המשוואה הבאה עבור התארכות המוט תחת דפורמציה צירית:

נוסחה:

הצורה בה העיבור משתנה עם תלוי בעומסים המופעלים על המוט, אם שטח החתך משתנה עם ואם יש שינוי בתכונותיו של החומר לאורך . נעסוק כעת במקרה האחרון - תכונות החומר.

חוק הוק למאמץ צירי

נביט במקרה הפשוט של חומר באזור האלסטי שלו כאשר הטמפרטורה שלו נשארת קבועה, ואין מאמצים בצירים האחרים (), מתקיים חוק הוק:

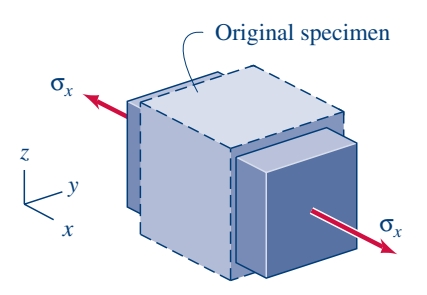
משוואה זו נותנת לנו את חילוק המאמץ הצירי על החתך במקום . רוב הדיפורמציות הציריות הן הומוגוניות, כך שמודול יאנג, , הוא קבוע לאורך המוט.

עיבור צירי כללי

עבור מקרים בהם הדגם מאוד דק, כך שרק מאמץ צירי מופעל עליו (ו- ו- זניחים), אז נוכל לקבל את העיבור הכללי (לפי חוק הוק למאמץ צירי, עיבור תרמי ועיקרון הסופרפוזיציה):

נוסחה:

משווואת הדפורמציה הצירית

נוכל לסכם את כל המשוואות שמצאנו עד כה במשוואה אחת. מחוק הוק למאמץ ומאמץ צירי נסיק כי:

ממשוואת התארכות נוכל לרשום:

לפי סימוני הקורס, נכתוב את משוואה זו בצורה הבאה:

נוסחה:

במקרה הפרטי בו כוח הנורמל ושטח החתך אחידים לאורך כל המוט, אנו נקבל:

כלומר:

נוסחה:

נשים לב שזהו פשוט המקרה של חוק הוק הקלאסי, כאשר . קיבלנו שקבוע “הקפיץ” תלוי בשטח החתך, האורך של המוט, ומודול יאנג - תכונה של החומר.

נתייחס למקרה היותר כללי, בו יש גם עיבור תרמי:

מאחר ו-:

נוכל לסכם:

או, לפי סימוני הקורס:

נוסחה:

אם הכוח, שטח החתך, מודול יאנג, והמקדם התרמי אחידים לאורך המוט, כלומר:

אזי נוכל לרשום:

ואז:

נוסחה:

תרגילים:

1. נתון:
   
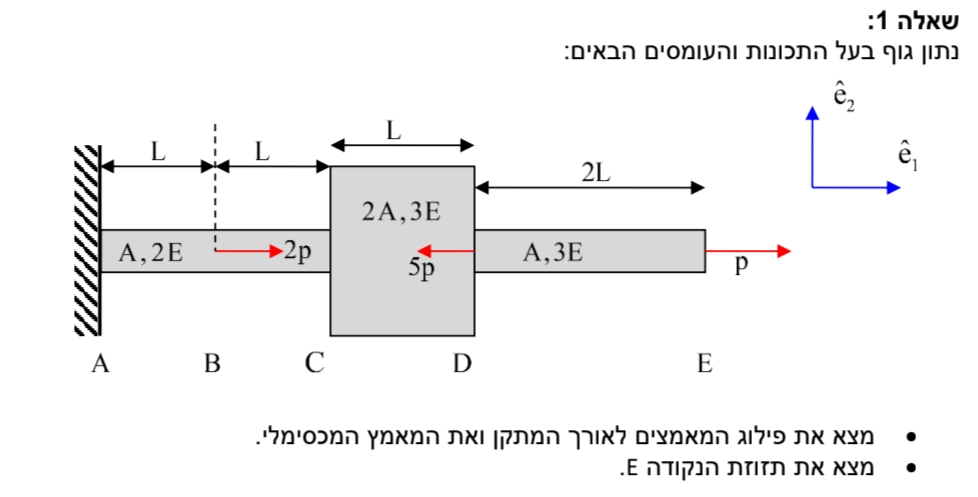
   פתרון:
   • נמצא את פילוג המאמצים - נבצע חתכים:
     
     • נמצא את :
     כלומר, קיבלנו כי האלמנט כולו התקצר.

תזוזות ועיבורים במסבכים פשוטים

אלגוריתם: שיטת ההעתקים לדיפורמציות ציריות

שיטת ההעתקים היא שיטה מאוד אלגברית לפתירת בעיות מסוימות סטטית, או לא. ע”י שיטה זו ניתן לפתור בו בזמן את משוואות שיווי המשקל הכתובות בעזרת העתקים לא ידועים.

שיטה זו מרחיבה את שיטת הצמתים לבעיות עם אלמנטים תחת דפורמציה. נתחיל מדוגמה:

דוגמה:

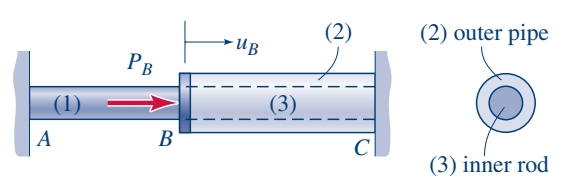
המבנה הבא מורכב משלושה חלקים אחידים:

דגם (1) הוא מוט קשיח. דגם (2) הוא צינור שמקיף את דגם (3), שהוא מוט קשיח שזהה לדגם (1). שלושת החלקים מחוברים בנקודה למשטח בעל עובי זניח.
ללא כוח חיצוני ב-, שלושת החלקים יושבים בול בין שני קירות בנקודות ו-.
מצאו ביטוי המקשר בין ההעתק בנקודה לכוח הצירי המופעל שם. בנוסף, מצאו ביטוי לכוחות הציריים בשלושת החלקים בתלות בכוח .
פתרון:
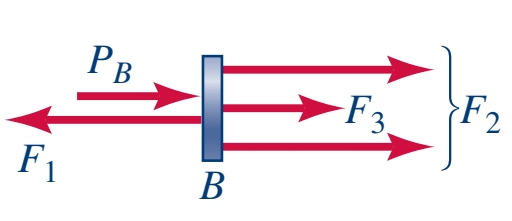
ניתן לחשוב על מבנה זה כמורכב משלושה חלקים אחידים וחיבור אחד בינהם, . עבור , נשרטט דג”ח:

משוואת שיווי משקל:

משוואה זו מקשרת בין שלושה כוחות פנימיים לא ידועים לכוח חיצוני ידוע. מאחר ויש שלושה כוחות לא ידועים, הבעיה לא מסויימת סטטית. לכן, נצטרך להביט בדפורמציה הצירית, ובגאומטריית הדפורמציה כדי להשיג עוד מידע.

יש לנו שלושה דגמים אחידים, תחת דפורמציה צירית, ועבור כל אחד מהם אנו יכולים לרשום:

במשוואה זו, ה--ים הם התארכויות הדגמים השונים. מתיחה חיובית, היא התארכות חיובית , מאחר וה- הם לפי הגדרה, חיוביים.

בנוסף, לפי האיור, אנו יכולים בקלות לקשר בין התארכות שלושת החלקים לההעתק , לפי הקשר :

כאשר השתמשנו בעובדה שההעתקים ב- ו- הם - הם לא זזים.
כעת, ע”י יש לנו שישה משוואות בשישה נעלמים. נציב את (3) לתוך (2) כדי לקבל:

נציב את זה ב-(1):

ולכן הפתרון הוא:

השיטה של הצבת הדפורמציה הגאומטרית, משוואה (3), בדפורמציה הצירית, משוואה (2), נקראת שיטת ההעתקים, מאחר וחלק עיקרי בפתרון, משוואה (6), נותן תשובה שהיא העתק.

נמצא כעת את הכוחות.
נציב פשוט את (6) ב-(4):

נשים לב שבפתרון שלנו, כל עלייה בקשיחות של אחד מהדגמים, יגרום לירידה בהעתק . בנוסף, ממשוואה (7), כל ירידה באחד מה-, יגרום לכך שהחלק שהכוח מפעיל על הדגם , יגדל.

נסכם את שלבי הפתרון שלנו:

1. נשרטט דג”ח ונרשום משוואות שיווי משקל לגופים כדי לקשר בין הכוחות החיצוניים לכוחות הפנימיים הלא ידועים.
2. נרשום את משווואת הדפורמציה הצירית לכל אחת מהדגמים העוברים עיבור:
3. נמצא את גאומטריית הדפורמציה כדי לקשר בין התארכות אלמנט, , לההעתקים במערכת - ניעזר בדג”ח.
4. נציב את הדפורמציה הגאומטרית במשוואות הדפורמציה. נקבל את הביטויים של הכוחות במובנים של ההעתקים במערכת.
5. נציב את התוצאות משלב 4 לתוך המשוואות משלב 1. זה נותן לנו את משוואות השיווי משקל במובנים של ההעתקים במערכת.
6. נפתור את המשוואה משלב 5, כדי לקבל את ההעתקים במערכת.
7. כדי למצוא את הכוחות, נציב את ההעתקים משלב 6 למשוואות משלב 4.
8. נעבור שוב על הפתרון כדי לוודא ששיווי משקל מתקיים, והביטויים הגיוניים מבחינה אינטואיטיבית.

תזוזות במסבכים פשוטים

נביט בעוד בעיה לא מסוימת סטטית, במסבך, כאשר נשים לב שבמקרה של מסבכים, בגאומטריית הדפורמציה, לכל צומת יכולה להיות התארכות ו-:

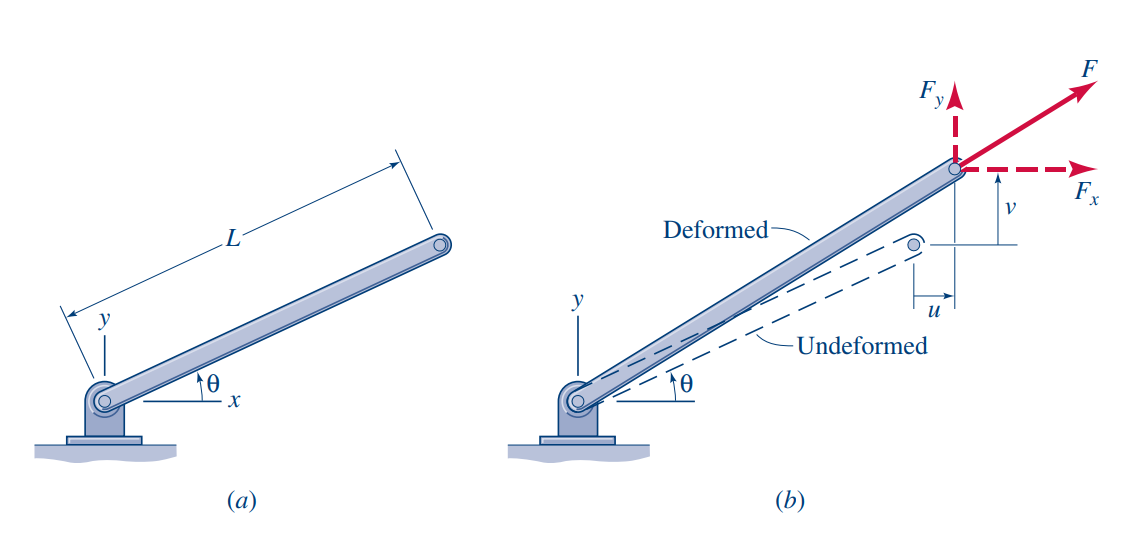
נניח ש- ו- מאוד קטנים יחסית ל-. אנו צריכים ביטוי שיקשר בין ל- ו-. מאחר ו- ו- קטנים, אנו יכולים למצוא את תרומתם ל- ע”י הטלתם על כיוון האלמנט המקורי, כאשר הזווית של האלמנט, , ידועה:

נוסחה:

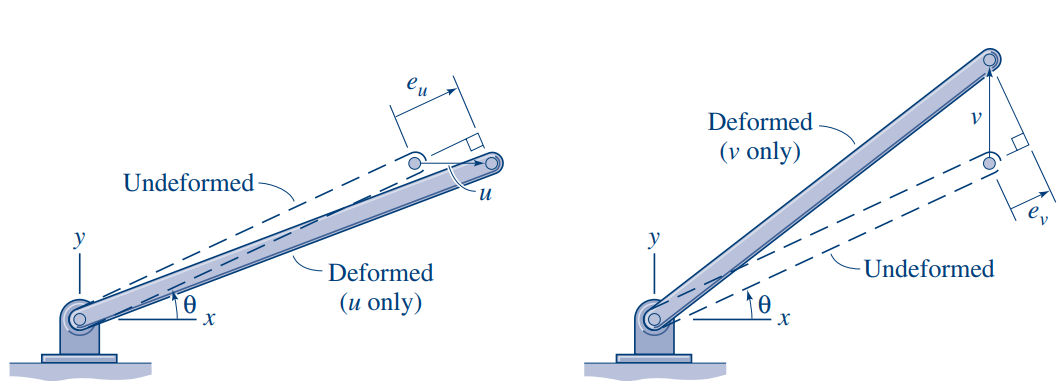
לפי סימוני הקורס, בהינתן הזזה של קטע לקטע , ההתארכות הכוללת היא:

לסיכום:

נוסחה:

דוגמה:

(מידות לא סטנדרטיות, לא רלוונטי לשיטת הפתרון).
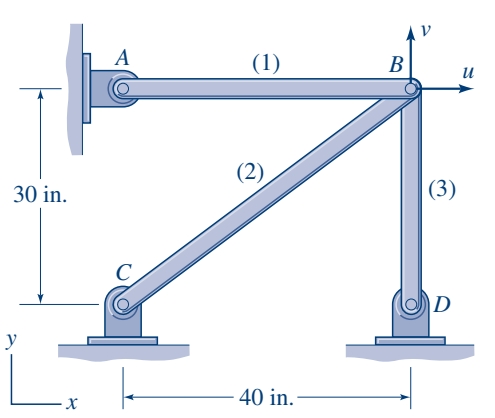
מסבך בעל שלושה אלמנטים נתון באיור הבא:

נתון כי השטח חתך לכל אחד מהמוטות הוא:

בנוסף, הם כולם עשויים מאלומיניום, . כאשר המוטות נוצרו, (1) ו-(3) נוצרו כמו שצריך (אורכים מדויקים, ו-). אבל, מוט (2) בעלת אורך , במקום האורך הנכון, . אם אלמנט (2) מוארך כך שפין יכול להיכנס כדי לחבר את כל המוטות בנקודה , ואז עוזבים את המערכת אז:
מהם ההעתקים , ו-?
מהם הכוחות הפנימיים בשלושת המוטות?
פתרון:
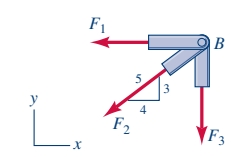
ניעזר בשיטת ההעתקים. דג”ח:

משוואות שיווי משקל:

קיבלנו:

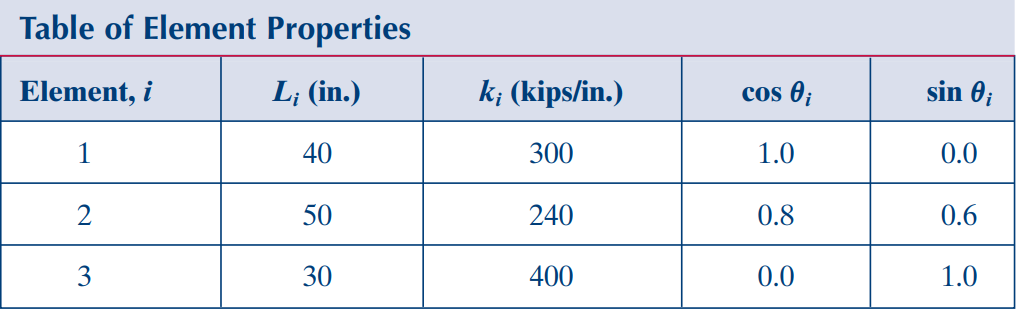
משוואות דפורמציה צירית: יש לנו שלושה אלמנטים, אז נרשום את המשוואות לכל אחד מהם. נחשב קודם את ה--ים שלהם, כאשר ניעזר בטבלה הבא:

אז, לפי משווואת הדפורמציה הצירית:

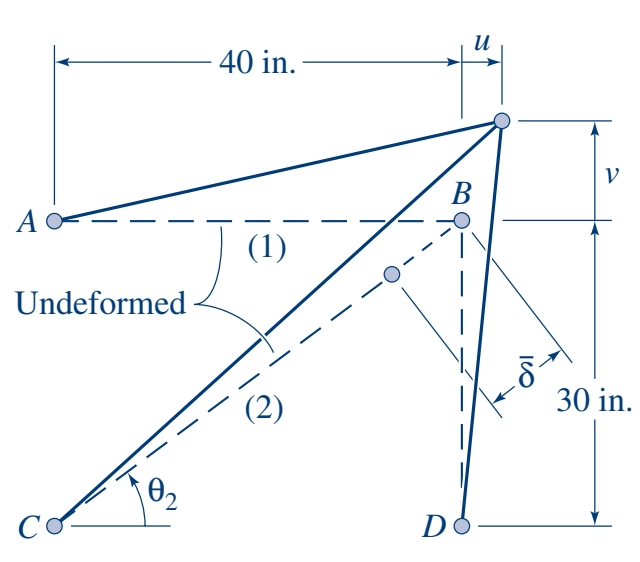
גאומטריית הדפורמציה: נשרטט דיאגרמת דפורמציה:

השרטוט מגזים את המרווח בין (2) והנקודה .
לכל אחד מההתארכויות:

מאחר וכל המוטות מחוברות יחד בנקודה :

לכן:

נשלב את משוואות (1) עד (3) בסדר :

כעת, מ-(1) ו-(4) יש לנו:

או:

נפתור ונקבל:

נמצא את הכוחות ע”י הצבה של - ו- ב-(4):

תרגילים:

1. נתונה קורה קשיחה לחלוטין בעלת אורך הנתמכת ע”י סמך חסר חיכוך ב-. בנקודה הקורה (אורך ) מחוברת לקורה ע”י פרק חסר חיכוך. בנקודה מחובר מוט הנתמך ע”י שני פרקים חסרי חיכוך בנקודה ו-. בין הנקודה לרצפה קיים מרווח , כאשר .
   נתוני חומר: , .
   שטח החתך של הרכיבים: .
   מקדמי התפשטות של הרכיבים: .
   
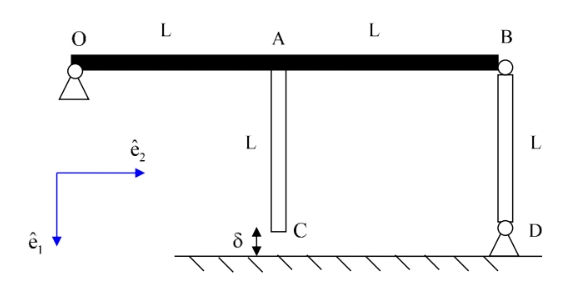
   • כאשר המערכת מועמסת ע”י (המופעלת בנקודה ), מהו הכוח המינימאלי שיגרום לסגירת המרווח ?
     פתרון:
     
     נבצע את החתך המשורטט:
     
     לפי שיקולי כוחות: העתקי הנקודות: נשים לב כי:
     
     נשתמש בדמיון משולשים: ולכן: וכעת:
     • נתון כי:
     וכי כוח זה גדול מהכוח הדרוש לסגירת המרווח . מהו המאמץ המוט ?
     פתרון: כעת מאלגברה: ונקבל:
     • מחממים את המוט ב-. מהו אשר דרוש לסגירת המרווח ?
       פתרון:
     נקבל כי:
     • מחממים את המוט עד לשינוי טמפרטורה של , מהו הכוח הפנימי במוט ?
       פתרון:
       נעשה סכום מומנטים ב-:
       
       נקבל:
     נתייחס לעיבור התרמי:

→ קודם: SLD1_006הבא: SLD1_008 ←