PHY3_006 פיזיקה אטומית ב

→ קודם: PHY3_005הבא: PHY3_007 ←

פרשנות פיזיקלית של המספרים הקוונטיים

המספר הקוונטי הראשי של מצב מסוים באטום המימן קובע את האנרגיה של האטום על פי משוואה (SJ41.21). כעת בואו נראה למה המספרים הקוונטיים האחרים במודל האטומי שלנו מתאימים מבחינה פיזיקלית.

המספר הקוונטי המסלולי

נתחיל דיון זה על ידי חזרה קצרה למודל בוהר של האטום. אם האלקטרון נע במעגל ברדיוס , גודל המומנט הזוויתי שלו יחסית למרכז המעגל הוא . כיוון מאונך למישור המעגל ונתון על ידי כלל יד ימין.

על פי הפיזיקה הקלאסית, הגודל של המומנט הזוויתי המסלולי יכול לקבל כל ערך. מודל בוהר של מימן, עם זאת, מניח שגודל המומנט הזוויתי של האלקטרון מוגבל לכפולות של ; כלומר, . מודל זה חוזה (בצורה שגויה) שמצב היסוד של מימן בעל יחידה אחת של תנע זוויתי.

קושי זה ואחרים נפתרים עם המודל הקוונטי-מכני של האטום, למרות שעלינו לוותר על הייצוג הנוח של אלקטרון המקיף במסלול עגול מוגדר היטב. למרות היעדר ייצוג זה, לאטום אכן יש תנע זוויתי והוא עדיין נקרא תנע זוויתי מסלולי.

על פי המכניקה הקוונטית, המומנט הזוויתי המסלולי קשור למספר הקוונטי . אטום במצב שהמספר הקוונטי הראשי שלו הוא יכול לקבל את הערכים הבדידים הבאים של גודל המומנט הזוויתי המסלולי:

בהינתן הערכים המותרים הללו של , אנו רואים ש- (המתאים ל-) הוא ערך מקובל של גודל המומנט הזוויתי. תוצאה זו אינה עקבית עם הערך של ממודל בוהר, כאשר המומנט הזוויתי של מצב היסוד הוא .

בפרשנות הקוונטית-מכנית, ענן האלקטרונים עבור המצב הוא סימטרי כדורית ואין לו ציר סיבוב יסודי.

הערה חשובה:

איור 6.1: נפוץ לייחס את המספרים הקוונטיים לאלקטרון. זכרו, עם זאת, שהמספרים הקוונטיים הללו נובעים ממשוואת שרדינגר, שכוללת פונקציית אנרגיה פוטנציאלית עבור המערכת של האלקטרון והגרעין. לכן, נכון יותר לייחס את המספרים הקוונטיים לאטום, אך נפוץ יותר לייחס אותם לאלקטרון.

המספר הקוונטי המגנטי המסלולי

מכיוון שתנע זוויתי הוא וקטור, יש לציין את כיוונו. ניתן להראות שללולאת זרם יש מומנט מגנטי מתאים , כאשר הוא הזרם בלולאה ו- הוא וקטור מאונך ללולאה שגודלו הוא שטח הלולאה.

בתיאוריית בוהר, האלקטרון המקיף מייצג לולאת זרם. בגישה הקוונטית-מכנית לאטום המימן, אנו נוטשים את נקודת המבט של המסלול העגול של תיאוריית בוהר, אבל לאטום עדיין יש תנע זוויתי מסלולי. לכן, קיים מומנט מגנטי בשל תנע זוויתי זה.

על פי המכניקה הקוונטית, יש כיוונים בדידים מותרים עבור וקטור המומנט המגנטי . כיוונים בדידים אלה יכולים להימדד על ידי הפעלת שדה מגנטי (שנניח שכיוונו בציר ה-). מצב זה שונה מאוד מזה בפיזיקה הקלאסית, שבה כל הכיוונים מותרים.

מכיוון שהמומנט המגנטי של האטום יכול להיות קשור לוקטור המומנט הזוויתי , הכיוונים הבדידים של מתורגמים לכיוון של שמקוונט. קוונטיזציה זו אומרת ש- (ההטלה של לאורך ציר ה-) יכולה לקבל רק ערכים בדידים.

המספר הקוונטי המגנטי המסלולי מציין את הערכים המותרים של רכיב ה- של המומנט הזוויתי המסלולי על פי הביטוי:

הקוונטיזציה של הכיוונים האפשריים של ביחס לשדה מגנטי חיצוני נקראת לעתים קרובות קוונטיזציית מרחב.

בואו נבחן את הגדלים והכיוונים האפשריים של עבור ערך נתון של . זכרו ש- יכול לקבל ערכים החל מ- עד .

• אם , אז ; הערך היחיד המותר של הוא ו-.
• אם , אז ממשוואה (SJ41.27). הערכים האפשריים של הם , אז משוואה (SJ41.28) אומרת לנו ש- יכול להיות .
• אם , גודל המומנט הזוויתי המסלולי הוא . הערך של יכול להיות , המתאימים לערכי של , וכן הלאה.

איור 6.2: מודל וקטורי עבור . (a) ההקרנות המותרות על ציר ה- של המומנט הזוויתי המסלולי הן כפולות שלמות של . (b) מכיוון שרכיבי ה- וה- של וקטור המומנט הזוויתי המסלולי אינם מקוונטים, הוקטור נמצא על פני החרוט. (Serway et al., 2019).

איור 6.1 מראה מודל וקטורי המתאר קוונטיזציית מרחב עבור המקרה . שימו לב ש- לא יכול להיות מקביל או אנטי-מקביל ל- מכיוון שהערך המקסימלי של הוא , שהוא קטן מגודל המומנט הזוויתי (זכרו, הוא הטלה של על ציר ה-, כלומר, הכיוון של ).

וקטור המומנט הזוויתי יכול להיות מאונך ל-, מה שמתאים למקרה של ו-. הוקטור אינו מצביע בכיוון ספציפי אחד; רק רכיב ה- של הוקטור מוגדר.

אם היה ידוע בדיוק, כל שלושת הרכיבים , ו- היו מוגדרים, מה שאינו עקבי עם גרסת המומנט הזוויתי של עקרון האי-ודאות. כיצד ניתן לציין את הגודל ורכיב ה- של וקטור, אך הוקטור לא יהיה מוגדר לחלוטין?

לתשובה, שימו לב ש- ו- אינם מוגדרים לחלוטין כך ש- נמצא בכל מקום על פני החרוט שיוצר זווית עם ציר ה- כמוצג באיור 6.1. מהאיור, אנו רואים ש- גם מקוונטת ושערכיה מוגדרים דרך היחס:

אם האטום מונח בשדה מגנטי, האנרגיה היא אנרגיה נוספת עבור מערכת האטום-שדה מעבר לזו המתוארת במשוואה (SJ41.21). מכיוון שהכיוונים של מקוונטים, יש אנרגיות כוללות בדידות עבור המערכת המתאימות לערכים שונים של .

איור 6.3: אפקט זימן. (a) רמות אנרגיה עבור מצבי היסוד והמעורר הראשון של אטום מימן. (b) כאשר האטום שקוע בשדה מגנטי , המצב עם מתפצל לשלושה מצבים, מה שגורם לקווי פליטה ב-, ו-, כאשר הוא הסט התדירות של הפליטה הנגרם על ידי השדה המגנטי. (Serway et al., 2019).

איור 6.2 מראה מעבר בין שתי רמות אטומיות בהיעדר שדה מגנטי. כאשר מופעל שדה מגנטי, הרמה העליונה, עם , מתפצלת לשלוש רמות התואמות לכיוונים השונים של . יש כעת שלושה מעברים אפשריים מתת-הקליפה לתת-הקליפה . לכן, באוסף של אטומים, יש אטומים בכל שלושת המצבים והקו הספקטרלי היחיד מתפצל לשלושה קווים ספקטרליים. תופעה זו נקראת אפקט זימן.

אפקט זימן יכול לשמש למדידת שדות מגנטיים בחלל. לדוגמה, הפיצול של קווים ספקטרליים באור מאטומי מימן בפני השטח של השמש יכול לשמש לחישוב גודל השדה המגנטי באותו מקום.

אפקט זימן הוא אחת מתופעות רבות שאינן יכולות להיות מוסברות עם מודל בוהר אבל מוסברות בהצלחה על ידי המודל הקוונטי של האטום.

דוגמה: קוונטיזציית מרחב עבור מימן

איור 6.4: נבחן את אטום המימן במצב . חשבו את גודל , הערכים המותרים של והזוויות המתאימות ש- יוצר עם ציר ה-.

פתרון:

נחשב את גודל המומנט הזוויתי המסלולי באמצעות משוואה (SJ41.27):

נחשב את הערכים המותרים של באמצעות משוואה (SJ41.28) עם :

נחשב את הערכים המותרים של באמצעות משוואה (SJ41.29):

נמצא את הזוויות המתאימות לערכי הללו:

מה אם הערך של הוא מספר שלם שרירותי? עבור ערך שרירותי של , כמה ערכים של מותרים?

עבור ערך נתון של , הערכים של נעים מ- עד בצעדים של . לכן, יש ערכים לא-אפסיים של (ספציפית, ). בנוסף, ערך אחד נוסף של אפשרי, עבור סך של ערכים של .

המספר הקוונטי המגנטי הסיבובי

שלושת המספרים הקוונטיים , ו- שנדונו עד כה נוצרים על ידי החלת תנאי שפה על פתרונות משוואת שרדינגר, ואנו יכולים להקצות פרשנות פיזיקלית לכל מספר קוונטי. כעת בואו נבחן את ספין האלקטרון, שאינו נובע ממשוואת שרדינגר.

מצאנו ארבעה מצבים קוונטיים התואמים ל-. במציאות, עם זאת, מתרחשים שמונה מצבים כאלה. ניתן להסביר את ארבעת המצבים הנוספים על ידי דרישה למספר קוונטי רביעי לכל מצב, המספר הקוונטי המגנטי הסיבובי .

הצורך במספר קוונטי חדש זה נוצר מבחינה היסטורית בגלל תכונה חריגה שנצפתה בספקטרום של גזים מסוימים, כמו אדי נתרן. בחינה קרובה של קו בולט אחד בספקטרום הפליטה של נתרן מגלה שהקו הוא, למעשה, שני קווים קרובים הנקראים כפילות. האורכי הגל של קווים אלה מתרחשים באזור הצהוב של הספקטרום האלקטרומגנטי ב- ו-.

בשנת 1925, כאשר נצפתה כפילות זו לראשונה, לא ניתן היה להסבירה עם התיאוריה האטומית הקיימת. כדי לפתור דילמה זו, שמואל גודסמיט (1902-1978) וג’ורג’ אולנבק (1900-1988), בעקבות הצעה של הפיזיקאי האוסטרי וולפגנג פאולי, הציעו את מספר הקוונטי הסיבובי.

כדי לתאר מספר קוונטי חדש זה, נוח (אך שגוי מבחינה טכנית) לדמיין את האלקטרון מסתובב סביב צירו כשהוא מקיף את הגרעין. כפי שמוצג באיור הבא, בתיאוריה הקוונטית, קיימים רק שני כיוונים עבור ספין האלקטרון.

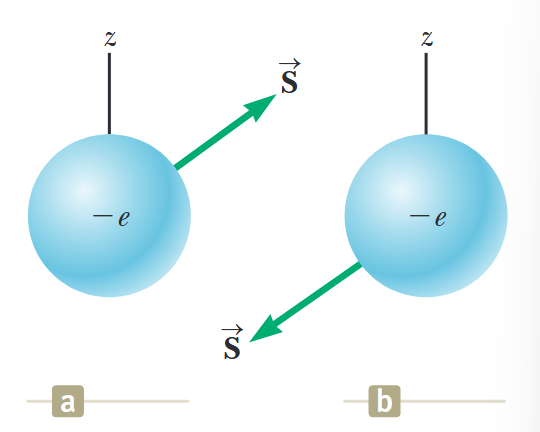
איור 6.5: הספין של אלקטרון יכול להיות (a) למעלה או (b) למטה יחסית לציר מוגדר. כמו במקרה של תנע זוויתי מסלולי, רכיבי ה- וה- של וקטור המומנט הזוויתי הסיבובי אינם מקוונטים. (Serway et al., 2019).

אם הכיוון של הספין הוא כפי שמוצג באיור 6.3 (a), נאמר שהאלקטרון עם ספין למעלה. אם הכיוון של הספין הוא כפי שמוצג באיור 6.3 (b), נאמר שהאלקטרון עם ספין למטה.

הערה חשובה:

איור 6.6: התיאור הקלאסי של ספין האלקטרון - כתוצאה של אלקטרון מסתובב - אינו נכון. התיאוריה החדשה יותר מצביעה על כך שהאלקטרון הוא חלקיק נקודתי, ללא הרחבה מרחבית. לכן, האלקטרון אינו מעוצב כעצם קשיח ואינו יכול להיחשב כמסתובב. למרות הקושי המושגי הזה, כל העדויות הניסויות תומכות ברעיון שלאלקטרון יש תנע זוויתי פנימי שניתן לתאר על ידי המספר הקוונטי המגנטי הסיבובי.

פול דיראק (1902-1984) הראה שהמספר הקוונטי הרביעי הזה נובע מהתכונות היחסותיות של האלקטרון.

בשנת 1921, אוטו שטרן (1888-1969) ווולטר גרלח (1889-1979) ביצעו ניסוי שהוכיח קוונטיזציית מרחב. התוצאות שלהם, עם זאת, לא היו בהתאמה כמותית עם התיאוריה האטומית שהתקיימה באותה תקופה.

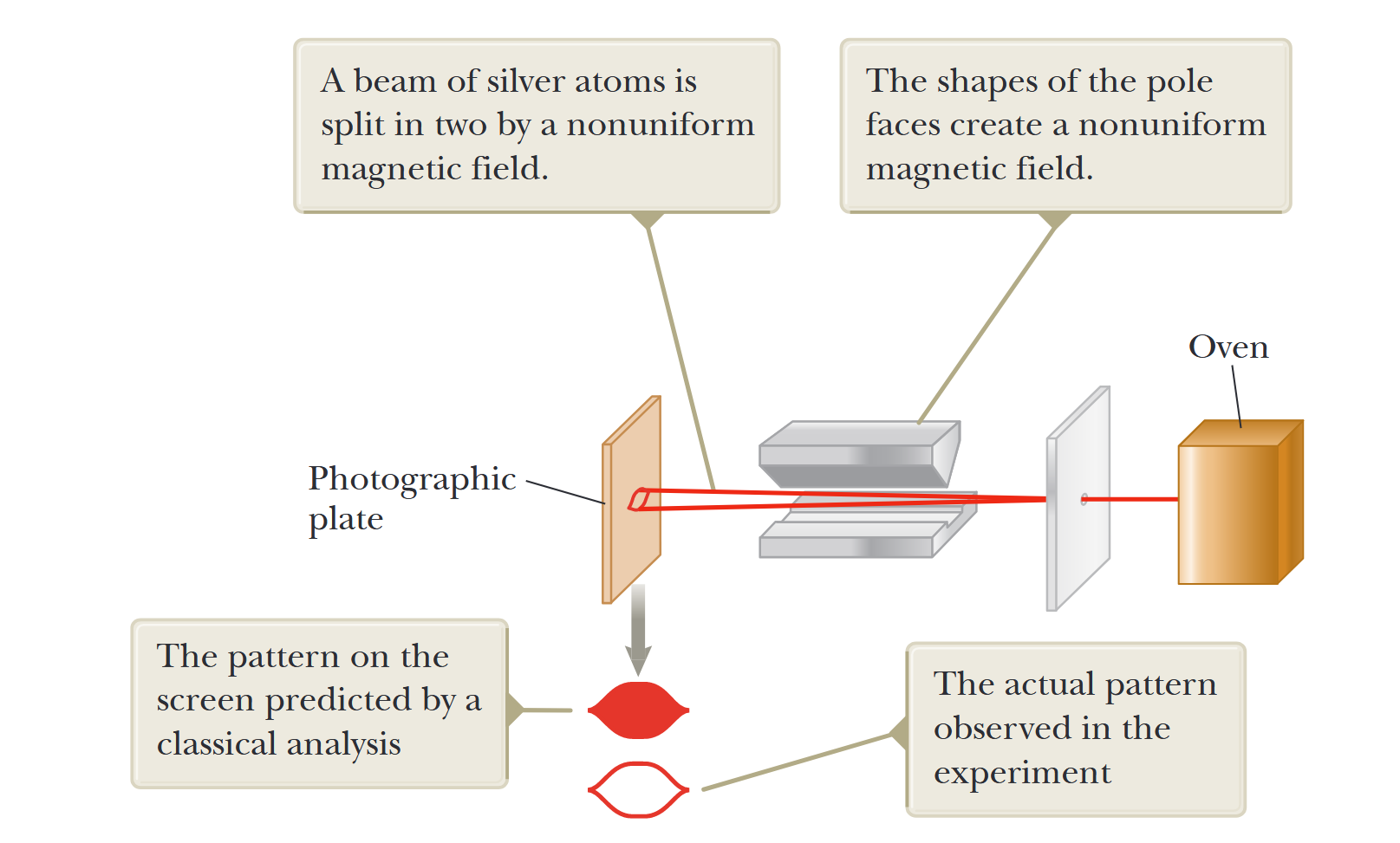
איור 6.7: הטכניקה שבה השתמשו שטרן וגרלח שהדגימה קוונטיזציית מרחב. קרן של אטומי כסף מתפצלת לשניים על ידי שדה מגנטי לא-אחיד. (Serway et al., 2019).

בניסויים שלהם, קרן של אטומי כסף נשלחה דרך שדה מגנטי לא-אחיד כמוצג באיור 6.4. האינטראקציה בין השדה המגנטי החיצוני והמומנט המגנטי של האטומים גורמת להסטה של האטומים בקרן מהכיוון הראשוני שלהם.

הטיעון הקלאסי הוא כדלקמן: אם כיוון ה- נבחר להיות כיוון חוסר האחידות המקסימלי של , הכוח המגנטי הנטו על האטומים הוא לאורך ציר ה- והוא פרופורציונלי לרכיב של המומנט המגנטי של האטום בכיוון ה-. מבחינה קלאסית, יכול לקבל כל כיוון, אז הקרן המוסטת צריכה להיות פרושה ברציפות.
זה לא מה שנצפה בניסוי. הקרן התפצלה לשני רכיבים בדידים ולא הראתה התפשטות רציפה. שטרן וגרלח חזרו על הניסוי עם אטומים אחרים, ובכל אחד מהמקרים, הקרן התפצלה לשניים או יותר רכיבים בדידים.

לפי המכניקה הקוונטית, לקרן המפוצלת אמור להיות מספר שלם של רכיבים בדידים, ומספר זה קובע את מספר הערכים השונים של . לכן, כיוון שניסוי שטרן-גרלח הראה התפצלות בדידה, קוונטיזציית מרחב הוכחה באופן איכותי.

נניח לרגע שהמומנט המגנטי של האטום הוא כתוצאה מתנע זוויתי. כיוון ש- פרופורציונלי ל-, מספר הערכים האפשריים של הוא . בנוסף לכך, כיוון ש- הוא מספר שלם, מספר הערכים של הוא תמיד אי-זוגי. אבל שטרן וגרלח קיבלו מספר זוגי של רכיבים בניסויים שלהם.

בשנת 1927, ט. א. פיפס וג’. ב. טיילור חזרו על הניסוי של שטרן-גרלח באמצעות קרן של אטומי מימן. הניסוי שלהם היה חשוב מכיוון שהוא כלל אטום המכיל אלקטרון יחיד במצב היסוד שלו, עבורו התיאוריה הקוונטית עושה תחזיות מהימנות.

זכרו ש- עבור מימן במצב היסוד שלו, אז . לכן, לא היינו מצפים שהקרן תוסט על ידי השדה המגנטי כלל מכיוון שהמומנט המגנטי של האטום הוא אפס.

הקרן בניסוי פיפס-טיילור, עם זאת, שוב התפצלה לשני רכיבים! על בסיס התוצאה הזו, עלינו להסיק שמשהו אחר מלבד התנועה המסלולית של האלקטרון תורם למומנט המגנטי האטומי.

כפי שלמדנו קודם, גודסמיט ואולנבק הציעו שלאלקטרון יש תנע זוויתי פנימי, ספין, מלבד המומנט הזוויתי המסלולי שלו. במילים אחרות, המומנט הזוויתי הכולל של האלקטרון במצב אלקטרוני מסוים מכיל גם תרומה מסלולית וגם תרומה סיבובית .

התוצאה של פיפס-טיילור אישרה את ההשערה של גודסמיט ואולנבק.

בשנת 1929, דיראק השתמש בצורה יחסותית של האנרגיה הכוללת של מערכת כדי לפתור את משוואת הגל יחסותית עבור האלקטרון בבאר פוטנציאל. הניתוח שלו אישר את הטבע הבסיסי של ספין האלקטרון.

ספין, כמו מסה ומטען, הוא תכונה פנימית של חלקיק, בלתי תלויה בסביבתו. יתר על כן, הניתוח הראה שניתן לתאר ספין אלקטרון על ידי מספר קוונטי יחיד , שערכו יכול להיות רק .

המומנט הזוויתי הסיבובי של האלקטרון לא משתנה אף פעם. מושג זה סותר חוקים קלאסיים, הקובעים שמטען מסתובב מאט בנוכחות שדה מגנטי בגלל חוק פאראדיי המלווה את השדה המשתנה.

יתר על כן, אם האלקטרון נתפס כמטען כדורי מסתובב הכפוף לחוקים קלאסיים, חלקים של האלקטרון ליד פני השטח שלו יהיו מסתובבים במהירויות העולות על מהירות האור. בסופו של דבר, הספין של האלקטרון הוא תכונה קוונטית שאינה ניתנת לתיאור קלאסי פשוט.

מכיוון שספין הוא צורה של תנע זוויתי, הוא חייב לעקוב אחר אותם כללים קוונטיים כמו תנע זוויתי מסלולי. בהתאם למשוואה (SJ41.27), גודל המומנט הזוויתי הסיבובי עבור האלקטרון הוא:

כמו תנע זוויתי מסלולי , תנע זוויתי סיבובי מציג קוונטיזציית מרחב. וקטור הספין יכול לקבל שני כיוונים יחסית לציר , המוגדרים על ידי המספר הקוונטי המגנטי הסיבובי .

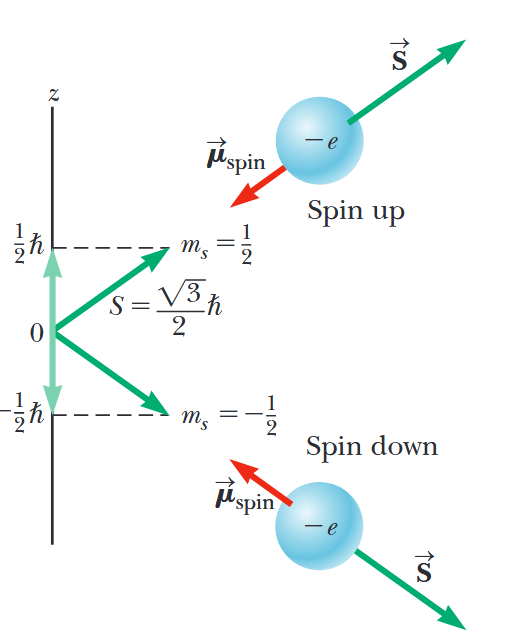
איור 6.8: המומנט הזוויתי הסיבובי מציג קוונטיזציית מרחב. איור זה מראה את שני הכיוונים המותרים של וקטור המומנט הזוויתי הסיבובי והמומנט המגנטי הסיבובי עבור חלקיק ספין-, כמו האלקטרון. (Serway et al., 2019).

בדומה למשוואה (SJ41.28) עבור תנע זוויתי מסלולי, רכיב ה- של תנע זוויתי סיבובי הוא:

שני הערכים עבור מתאימים לשני הכיוונים האפשריים עבור המוצגים באיור 6.5. הערך מתייחס למקרה ספין למעלה, ו- מתייחס למקרה ספין למטה.

שימו לב שמשוואות (SJ41.30) ו-(SJ41.31) אינן מאפשרות לוקטור הספין לשכב לאורך ציר ה-. הכיוון האמיתי של הוא בזווית גדולה יחסית ביחס לציר ה- כמוצג באיורים.

המומנט המגנטי הסיבובי של האלקטרון קשור למומנט הזוויתי הסיבובי שלו על ידי הביטוי:

כאשר הוא המטען האלקטרוני ו- הוא מסת האלקטרון. מכיוון ש-, רכיב ה- של המומנט המגנטי הסיבובי יכול לקבל את הערכים:

הגודל נקרא המגנטון של בוהר .

כיום, פיזיקאים מסבירים את הניסויים של שטרן-גרלח ופיפס-טיילור כדלקמן: המומנטים המגנטיים הנצפים עבור כסף ומימן נובעים מתנע זוויתי סיבובי בלבד, ללא תרומה מתנע זוויתי מסלולי.

בניסוי פיפס-טיילור, האלקטרון היחיד באטום המימן מקוונט בשדה המגנטי באופן שרכיב ה- של תנע זוויתי סיבובי הוא או , המתאימים ל-.

אלקטרונים עם ספין מוסטים כלפי מטה, ואלה עם ספין מוסטים כלפי מעלה.

בניסוי שטרן-גרלח, מתוך האלקטרונים של אטום הכסף נמצאים בתת-קליפות מלאות עם ספינים מזווגים. לכן, ל- אלקטרונים הללו תרומה נטו אפס גם לתנע זוויתי מסלולי וגם לסיבובי עבור האטום. המומנט הזוויתי של האטום נובע רק מהאלקטרון ה-. אלקטרון זה נמצא בתת-הקליפה , אז אין תרומה מתנע זוויתי מסלולי.

הניסוי של שטרן-גרלח סיפק שתי תוצאות חשובות:

1. אימות מושג קוונטיזציית המרחב
2. הראה שקיים תנע זוויתי סיבובי, למרות שתכונה זו לא הוכרה עד ארבע שנים לאחר ביצוע הניסויים

כפי שהוזכר קודם, יש שמונה מצבים קוונטיים התואמים ל- באטום המימן, לא ארבעה. כל אחד מארבעת המצבים הוא למעשה שני מצבים בגלל שני הערכים האפשריים של .

שני מצבי ה- של אטום המימן בטבלה אינם בעלי אותה אנרגיה. למעשה, ניתן לעשות מעבר בין שני המצבים. התוצאה היא פליטת פוטון באורך גל . קרינה זו מאטומי מימן בחלל חשובה מאוד למטרות אסטרו-פיזיקליות.

מספרים קוונטיים עבור המצב של מימן:

				תת-קליפה	קליפה	מספר מצבים בתת-קליפה

עקרון האיסור והטבלה המחזורית

מצאנו שמצבו של אטום המימן מאופיין על ידי ארבעה מספרים קוונטיים: , , ו-. מתברר שניתן לחזות את מספר המצבים הזמינים לאטומים אחרים מלבד מימן גם על ידי אותו מערך של מספרים קוונטיים. למעשה, ארבעת המספרים הקוונטיים הללו יכולים לשמש לתיאור כל המצבים האלקטרוניים של אטום, ללא קשר למספר האלקטרונים במבנה שלו. בדיון שלנו על אטומים עם אלקטרונים רבים, לעתים קרובות הכי קל להקצות את המספרים הקוונטיים לאלקטרונים באטום בניגוד לאטום כולו. שאלה ברורה שעולה כאן היא: “כמה אלקטרונים יכולים להיות במצב קוונטי מסוים?” פאולי ענה על שאלה חשובה זו בשנת 1925, בהצהרה הידועה כעקרון האיסור:

עקרון האיסור:

איור 6.9: שני אלקטרונים לא יכולים להיות אף פעם באותו מצב קוונטי; לכן, שני אלקטרונים באותו אטום לא יכולים להיות בעלי אותו מערך של מספרים קוונטיים.

אם עקרון זה לא היה תקף, אטום יכול היה לקרון אנרגיה עד שכל אלקטרון באטום נמצא במצב האנרגיה הנמוך ביותר האפשרי ולכן ההתנהגות הכימית של היסודות הייתה משתנה באופן גס. הטבע כפי שאנו מכירים אותו לא היה קיים. במציאות, אנו יכולים לראות את המבנה האלקטרוני של אטומים מורכבים כרצף של רמות מלאות עולה באנרגיה. ככלל כללי, סדר המילוי של תת-הקליפות של אטום הוא כדלקמן. ברגע שתת-קליפה מתמלאת, האלקטרון הבא נכנס לתת-הקליפה הריקה בעלת האנרגיה הנמוכה ביותר. אנו יכולים להבין התנהגות זו על ידי הכרה בכך שאם האטום לא היה במצב האנרגיה הנמוך ביותר הזמין לו, הוא היה מקרין אנרגיה עד שיגיע למצב זה. נטייה זו של מערכת קוונטית להשיג את מצב האנרגיה הנמוך ביותר עולה בקנה אחד עם החוק השני של התרמודינמיקה. האנטרופיה של היקום גדלה על ידי פליטת פוטונים על ידי המערכת, כך שהאנרגיה מתפזרת על פני נפח גדול יותר של חלל.

לפני שנדון בתצורה האלקטרונית של יסודות שונים, נוח להגדיר אורביטל כמצב האטומי המאופיין על ידי המספרים הקוונטיים , ו-. עקרון האיסור אומר לנו שמקסימום שני אלקטרונים יכולים להיות נוכחים בכל אורביטל. לאחד מאלקטרונים אלה יש מספר קוונטי מגנטי סיבובי , ולשני יש . מכיוון שכל אורביטל מוגבל לשני אלקטרונים, מספר האלקטרונים שיכולים לתפוס את הקליפות השונות מוגבל גם כן.

מצבים קוונטיים מותרים עבור האלקטרונים באטום עד :

קליפה		תת-קליפה

החצים המצביעים כלפי מעלה מציינים מצב המתואר על ידי , ואלה המצביעים כלפי מטה מציינים ש-. הקליפה יכולה להכיל רק שני אלקטרונים מכיוון ש- אומרת שרק אורביטל אחד מותר. (שלושת המספרים הקוונטיים המתארים אורביטל זה הם , ו-.) לקליפה יש שתי תת-קליפות, אחת עבור ואחת עבור . תת-הקליפה מוגבלת לשני אלקטרונים מכיוון ש-. לתת-הקליפה יש שלושה אורביטלים מותרים, המתאימים ל-. מכיוון שכל אורביטל יכול להכיל שני אלקטרונים, תת-הקליפה יכולה להכיל שישה אלקטרונים. לכן, הקליפה יכולה להכיל שמונה אלקטרונים. לקליפה יש שלוש תת-קליפות () ותשעה אורביטלים, המכילים עד אלקטרונים. באופן כללי, כל קליפה יכולה להכיל עד אלקטרונים.

ניתן להמחיש את עקרון האיסור על ידי בחינת הסידור האלקטרוני בכמה מהאטומים הקלים יותר. המספר האטומי של כל יסוד הוא מספר הפרוטונים בגרעין של אטום של אותו יסוד. לאטום ניטרלי של אותו יסוד יש אלקטרונים. למימן () יש רק אלקטרון אחד, שבמצב היסוד של האטום, ניתן לתאר על ידי אחד משני מערכי המספרים הקוונטיים : או . תצורה אלקטרונית זו מסומנת לעתים קרובות . הסימון מתייחס למצב שבו ו-, והמעריך מציין שאלקטרון אחד נוכח בתת-הקליפה . להליום () יש שני אלקטרונים. במצב היסוד, המספרים הקוונטיים שלהם הם ו-. אין שילובים אפשריים אחרים של מספרים קוונטיים עבור רמה זו, ואנו אומרים שהקליפה מלאה. תצורה אלקטרונית זו נכתבת . ללתיום () יש שלושה אלקטרונים. במצב היסוד, שניים מהם נמצאים בתת-הקליפה . השלישי נמצא בתת-הקליפה מכיוון שתת-קליפה זו נמוכה מעט יותר באנרגיה מתת-הקליפה .¹ לפיכך, התצורה האלקטרונית של ליתיום היא .

איור 6.10: מילוי המצבים האלקטרוניים חייב לציית גם לעקרון האיסור וגם לכלל הונד. (Serway et al., 2019).

התצורות האלקטרוניות של ליתיום והיסודות הבאים מסופקות באיור 6.6. התצורה האלקטרונית של בריליום (), עם ארבעת האלקטרונים שלו, היא , ולבורון () יש תצורה של . האלקטרון בבורון יכול להיות מתואר על ידי אחד מששת מערכי המספרים הקוונטיים בעלי הסתברות שווה. באיור 6.6, אנו מציגים את האלקטרון הזה באורביטל השמאלי ביותר עם ספין למעלה, אך הוא יכול להיות באותה מידה באורביטל כלשהו עם ספין למעלה או למטה.

לפחמן () יש שישה אלקטרונים, מה שמעלה שאלה לגבי איך להקצות את שני האלקטרונים . האם הם נכנסים לאותו אורביטל עם ספינים מזווגים (), או שהם תופסים אורביטלים שונים עם ספינים לא מזווגים ()? נתונים ניסיוניים מראים שהתצורה היציבה ביותר (כלומר, זו עם האנרגיה הנמוכה ביותר) היא האחרונה, שבה הספינים אינם מזווגים. לפיכך, שני האלקטרונים בפחמן ושלושת האלקטרונים בחנקן () בעלי ספינים לא מזווגים כפי שאיור 6.6 מראה. הכלל הכללי השולט במצבים כאלה, הנקרא כלל הונד, קובע כי:

כלל הונד:

איור 6.11: כאשר לאטום יש אורביטלים באנרגיה שווה, הסדר שבו הם מתמלאים באלקטרונים הוא כזה שקיים מספר מקסימלי של אלקטרונים בעלי ספינים לא מזווגים.

ישנם מספר יוצאי דופן לכלל זה ביסודות עם תתי-קליפות שקרובות להיות מלאות או מלאות למחצה.

בשנת 1871, הרבה לפני שהמכניקה הקוונטית פותחה, הכימאי הרוסי דימיטרי מנדלייב (1834-1907) עשה ניסיון מוקדם למצוא סדר כלשהו בין היסודות הכימיים. הוא ניסה לארגן את היסודות לתוכן העניינים של ספר שהוא כתב. הוא סידר את האטומים בטבלה דומה לזו המוצגת באיור, על פי המסות האטומיות שלהם והדמיון הכימי שלהם. הטבלה הראשונה שמנדלייב הציע הכילה מקומות ריקים רבים, והוא הצהיר באומץ שהפערים היו שם רק משום שהיסודות טרם התגלו. על ידי הבחנה בעמודות שבהן יסודות חסרים אמורים להיות ממוקמים, הוא הצליח לבצע חיזויים גסים לגבי תכונותיהם הכימיות. תוך 20 שנה מהודעה זו, רוב היסודות הללו אכן התגלו.

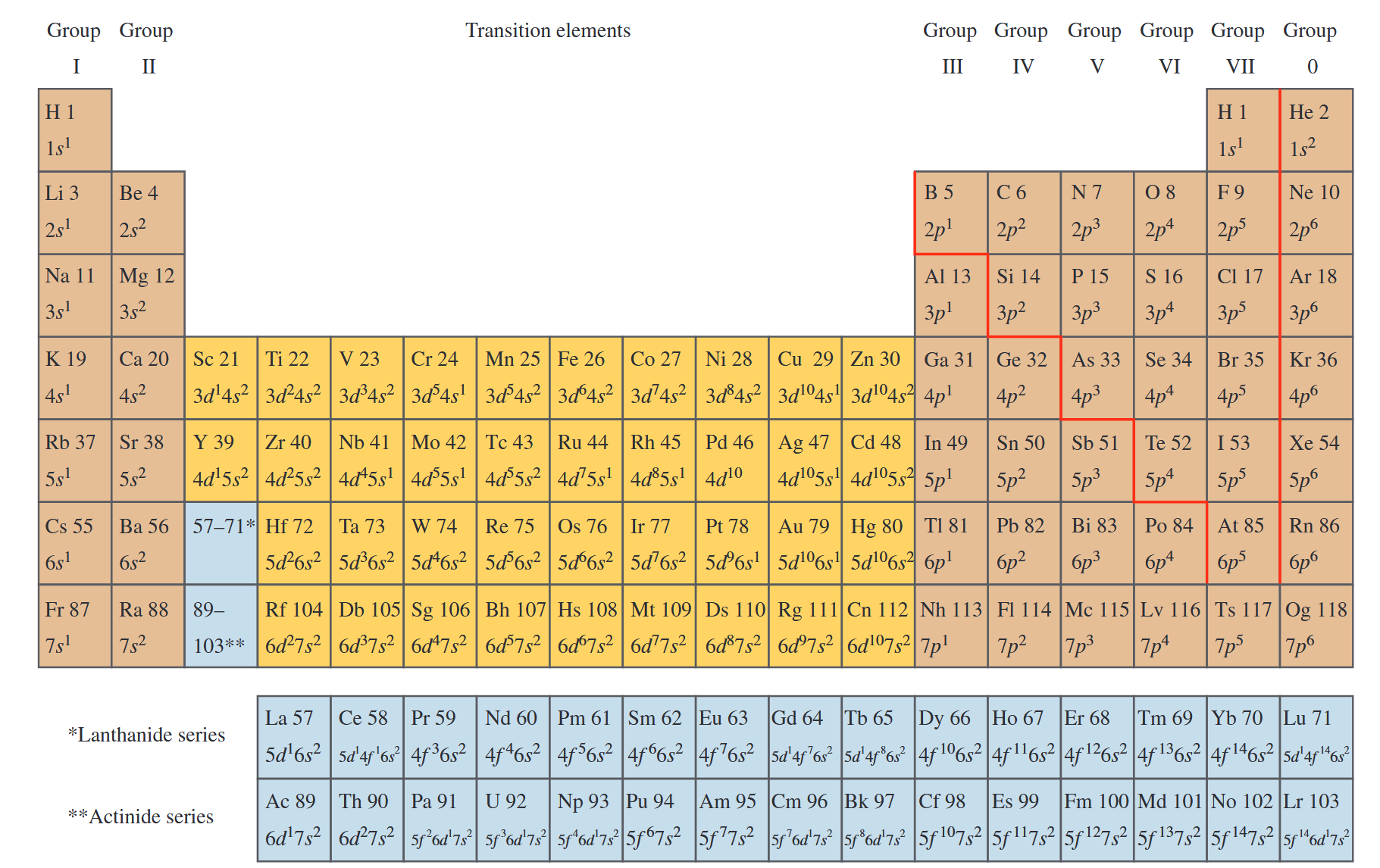
איור 6.12: הטבלה המחזורית של היסודות היא ייצוג טבלאי מאורגן של היסודות המראה את התנהגותם הכימית המחזורית. יסודות בעמודה נתונה בעלי התנהגות כימית דומה. טבלה זו מציגה את הסמל הכימי של היסוד, המספר האטומי והתצורה האלקטרונית. השורה השביעית הושלמה עם זיהוי שמות חדשים ליסודות 113 (nihonium), 115 (moscovium), 117 (tennessine) ו-118 (organesson) בדצמבר 2016. (Serway et al., 2019).

היסודות בטבלה המחזורית (איור) מסודרים כך שכל אלה בעמודה בעלי תכונות כימיות דומות. לדוגמה, הביטו ביסודות בעמודה האחרונה, שכולם גזים בטמפרטורת החדר: (הליום), (נאון), (ארגון), (קריפטון), (קסנון) ו- (רדון). המאפיין הבולט של כל היסודות הללו הוא שהם בדרך כלל אינם לוקחים חלק בתגובות כימיות; כלומר, הם אינם מצטרפים בקלות לאטומים אחרים ליצירת מולקולות. לכן הם נקראים גזים אינרטיים או גזים אצילים. לכל האטומים בעמודה זו יש תת-קליפה חיצונית מלאה והם בדרך כלל לא ישחררו אלקטרון או ייקחו אלקטרון מאטום אחר. לפיכך, התנהגותם האינרטית.

אנו יכולים להבין חלקית התנהגות זו על ידי הסתכלות על התצורות האלקטרוניות באיור. ההתנהגות הכימית של יסוד תלויה בקליפה החיצונית ביותר המכילה אלקטרונים. התצורה האלקטרונית עבור הליום היא , והקליפה (שהיא הקליפה החיצונית ביותר מכיוון שהיא הקליפה היחידה) מלאה. כמו כן, האנרגיה של האטום בתצורה זו נמוכה במידה ניכרת מהאנרגיה עבור התצורה שבה אלקטרון נמצא ברמה הזמינה הבאה, תת-הקליפה . לאחר מכן, הביטו על התצורה האלקטרונית עבור נאון, . שוב, הקליפה החיצונית ביותר ( במקרה זה) מלאה ופער רחב באנרגיה קיים בין תת-הקליפה המלאה לתת-קליפה הזמינה הבאה, תת-הקליפה . לארגון יש את התצורה . כאן, רק תת-הקליפה מלאה, אך שוב פער רחב באנרגיה מתרחש בין תת-הקליפה המלאה לתת קליפה הזמינה הבאה, תת-הקליפה . דפוס זה נמשך דרך כל הגזים האצילים. לקריפטון יש תת-קליפה מלאה, לקסנון תת-קליפה מלאה, ולרדון תת-קליפה מלאה. אטומים מעטים מדי של organesson התגלו כדי לקבוע את התנהגותו הכימית.

העמודה משמאל לגזים האצילים בטבלה המחזורית מורכבת מקבוצת יסודות הנקראים הלוגנים: פלואור, כלור, ברום, יוד וכן הלאה. בטמפרטורת החדר, פלואור וכלור הם גזים, ברום הוא נוזל, ויוד ואסטטין הם מוצקים. בכל אחד מהאטומים הללו, תת-הקליפה החיצונית חסרה אלקטרון אחד מלהיות מלאה. כתוצאה מכך, ההלוגנים פעילים מאוד מבחינה כימית- הם מקבלים בקלות אלקטרון מאטום אחר ליצירת קליפה סגורה. ההלוגנים נוטים ליצור קשרים יוניים חזקים עם אטומים בצד השני של הטבלה המחזורית. Tennessine עשוי להיות בעל התנהגות כימית שונה.

בצד השמאלי של הטבלה המחזורית, יסודות קבוצה I מורכבים ממימן והמתכות האלקליות: ליתיום, נתרן, אשלגן, רובידיום, צסיום ופרנציום. כל אחד מהאטומים הללו מכיל אלקטרון אחד בתת-קליפה מחוץ לתת-קליפה סגורה. לכן, יסודות אלה יוצרים בקלות יונים חיוביים מכיוון שהאלקטרון הבודד קשור באנרגיה נמוכה יחסית ומוסר בקלות. לכן, אטומי המתכת האלקלית פעילים כימית ויוצרים קשרים חזקים מאוד עם אטומי הלוגן. לדוגמה, מלח שולחן, , הוא שילוב של מתכת אלקלית והלוגן. מכיוון שהאלקטרון החיצוני של אטום אלקלי קשור אליו באופן די חלש, מתכות אלקליות טהורות נוטות להיות מוליכים חשמליים טובים. בגלל הפעילות הכימית הגבוהה שלהם, עם זאת, הם בדרך כלל לא נמצאים בטבע בצורה טהורה.

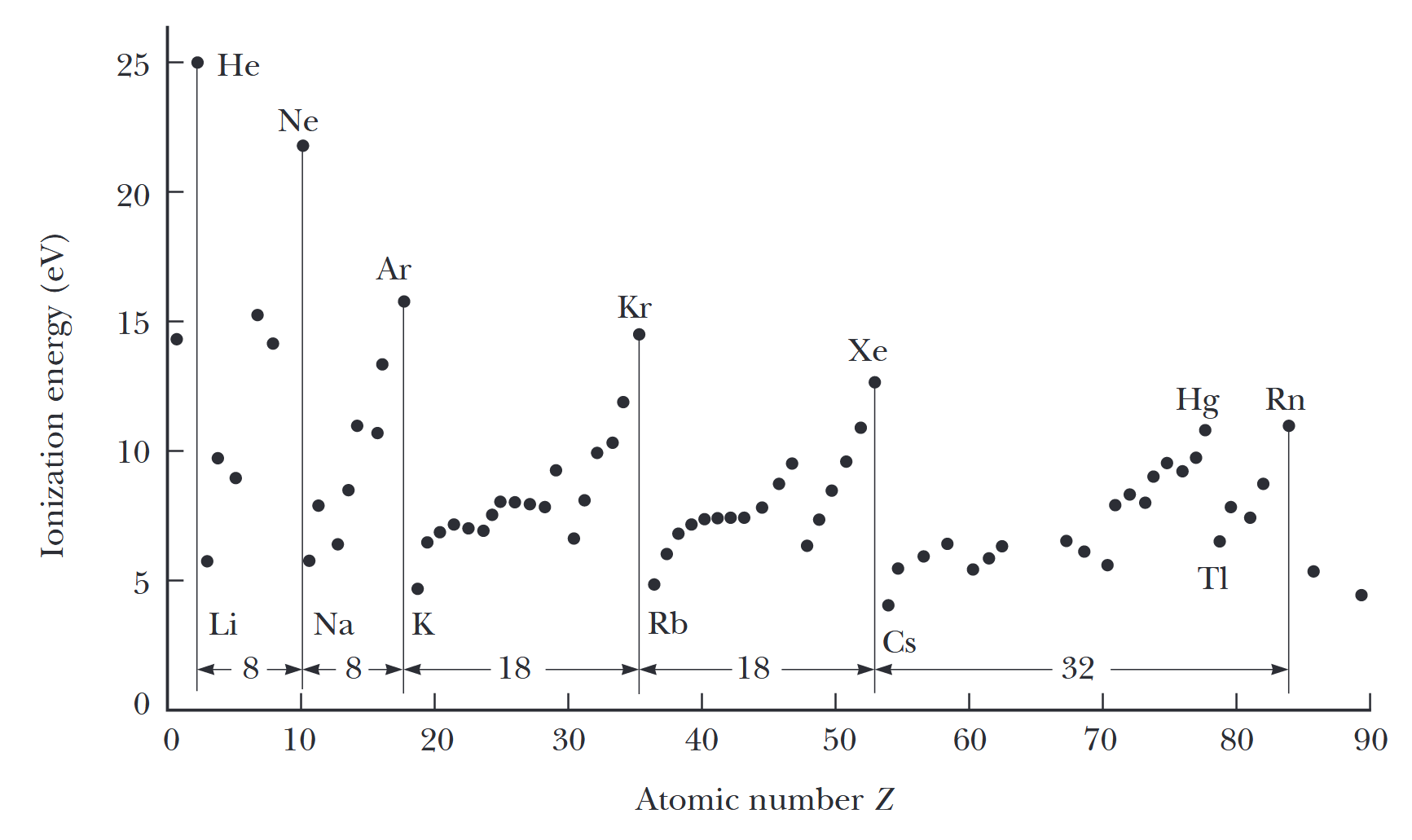
איור 6.13: אנרגיית היינון כפונקציה של המספר האטומי . (Serway et al., 2019).

באיור 6.7 משורטט אנרגיית היינון מול המספר האטומי . שימו לב לדפוס של עבור השיאים השונים. דפוס זה נובע מעקרון האיסור ועוזר להסביר מדוע היסודות חוזרים על תכונותיהם הכימיות בקבוצות. לדוגמה, השיאים ב- מתאימים לגזים האצילים הליום, נאון, ארגון וקריפטון, בהתאמה. שכפי שהזכרנו, לכולם יש קליפות חיצוניות מלאות. ליסודות אלה יש אנרגיות יינון גבוהות יחסית והתנהגות כימית דומה.

קרינה נראית וקרני רנטגן

בפרק קודם דנו בתצפית ובפרשנות המוקדמת של קווים ספקטרליים מגזים. מקורם של קווים ספקטרליים נמצאים במעברים בין מצבים אטומיים מקוונטים. דיאגרמת רמות אנרגיה מותאמת עבור מימן מוצגת באיור 6.8. בדיאגרמה זו, הערכים המותרים של עבור כל קליפה מופרדים אופקית. איור 6.8 מראה רק את המצבים עד ; לקליפות מ- כלפי מעלה יהיו עוד מצבים מימין, שאינן מוצגות.

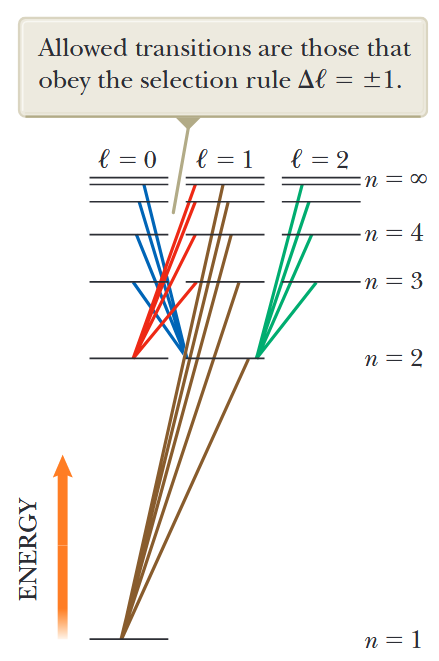
איור 6.14: כמה מעברים אלקטרוניים מותרים עבור מימן, המיוצגים על ידי הקווים הצבעוניים. מעברים מותרים הם אלה שמציתים לכלל הבחירה . (Serway et al., 2019).

מעברים שבהם אינו משתנה הם בעלי הסתברות נמוכה מאוד להתרחש והם נקראים מעברים אסורים. (מעברים כאלה למעשה יכולים להתרחש, אך ההסתברות שלהם נמוכה מאוד ביחס להסתברות של מעברים “מותרים”.) הקווים האלכסוניים השונים מייצגים מעברים מותרים בין מצבים נייחים. כל מעבר שאטום מבצע ממצב אנרגיה גבוה יותר לנמוך יותר, נפלט פוטון. התדירות של פוטון זה היא , כאשר היא הפרש האנרגיה בין שני המצבים ו- הוא קבוע פלאנק. כללי הבחירה עבור המעברים המותרים הם:

איור 6.8 מראה שהמומנט הזוויתי המסלולי של אטום משתנה כאשר הוא עושה מעבר למצב אנרגיה נמוך יותר. לכן, האטום לבדו הוא מערכת לא מבודדת עבור מומנט זוויתי. אם נבחן את מערכת האטום-פוטון, עם זאת, היא חייבת להיות מערכת מבודדת עבור מומנט זוויתי מכיוון ששום דבר אחר לא מקיים אינטראקציה עם מערכת זו. הפוטון המעורב בתהליך חייב לשאת מומנט זוויתי הרחק מהאטום כאשר המעבר מתרחש. למעשה, לפוטון יש מומנט זוויתי שווה לזה של חלקיק בעל ספין של . קבענו כעת על פני כמה פרקים שלפוטון יש אנרגיה, תנע קווי ומומנט זוויתי, וכל אחד מאלה נשמר בתהליכים אטומיים.

זכרו ממשוואה (SJ41.21) שהאנרגיות המותרות עבור אטומים ויונים חד-אלקטרוניים, כמו מימן ו-, הן:

משוואה זו פותחה מתיאוריית בוהר, אך היא משמשת כקירוב ראשון טוב גם במכניקה הקוונטית. עבור אטומים רב-אלקטרוניים, המטען הגרעיני החיובי מוסתר במידה רבה על ידי המטען השלילי של האלקטרונים בקליפות הפנימיות. לכן, האלקטרונים החיצוניים מקיימים אינטראקציה עם מטען שהוא למעשה קטן יותר מהמטען הגרעיני. לביטוי עבור האנרגיות המותרות עבור אטומים רב-אלקטרוניים יש את אותה צורה כמו משוואה (SJ41.35) כאשר מוחלף במספר אטומי אפקטיבי :

כאשר תלוי ב- וב-.

ספקטרום קרני רנטגן

קרני רנטגן נפלטות כאשר אלקטרונים בעלי אנרגיה גבוהה או כל חלקיקים טעונים אחרים מפגיזים מטרת מתכת. ספקטרום קרני הרנטגן מורכב בדרך כלל מפס רציף רחב המכיל סדרה של קווים חדים כפי שמוצג באיור 6.9. הזכרנו שמטען חשמלי מואץ פולט קרינה אלקטרומגנטית. קרני הרנטגן באיור 6.9 הן התוצאה של האטה של אלקטרונים בעלי אנרגיה גבוהה כאשר הם פוגעים במטרה. ייתכן שיידרשו כמה אינטראקציות עם אטומי המטרה לפני שהאלקטרון מוסר את כל האנרגיה הקינטית שלו. כמות האנרגיה הקינטית שנמסרת בכל אינטראקציה יכולה להשתנות מאפס ועד לכל האנרגיה הקינטית של האלקטרון. לכן, אורך הגל של הקרינה מהאינטראקציות הללו נמצא בטווח רציף מערך מינימלי מסוים ועד אינסוף. ההאטה הכללית הזו של האלקטרונים היא שמספקת את העקומה הרציפה באיור 6.9, המראה את הקטיעה של קרני רנטגן מתחת לערך אורך גל מינימלי התלוי באנרגיה הקינטית של האלקטרונים הנכנסים.

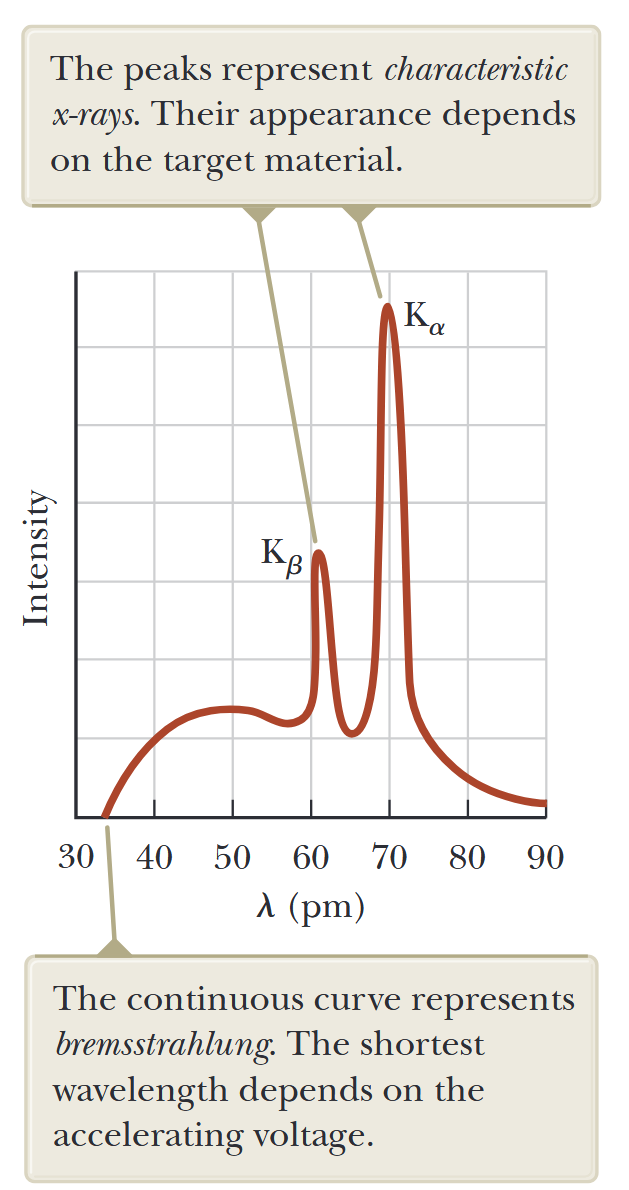
איור 6.15: ספקטרום קרני הרנטגן של מטרת מתכת. הנתונים שהוצגו הושגו כאשר אלקטרונים של הפגיזו מטרת מוליבדן. השיאים מייצגים קרני רנטגן אופייניות. הופעתם תלויה בחומר המטרה. העקומה הרציפה מייצגת bremsstrahlung. אורך הגל הקצר ביותר תלוי במתח המאיץ. (Serway et al., 2019).

קרינת רנטגן שמקורה בהאטה של אלקטרונים נקראת bremsstrahlung, המילה הגרמנית ל”קרינת בלימה”. bremsstrahlung באנרגיה גבוהה ביותר יכול לשמש לטיפול ברקמות סרטניות.

הקווים הבדידים באיור 6.9, הנקראים קרני רנטגן אופייניות והתגלו בשנת 1908, יש להם מקור שונה. מקורם נשאר בלתי מוסבר עד שפרטי המבנה האטומי הובנו. השלב הראשון בייצור קרני רנטגן אופייניות מתרחש כאשר אלקטרון מתנגש באטום. האלקטרון חייב להיות בעל אנרגיה מספקת כדי להסיר אלקטרון מקליפה פנימית מהאטום. החלל הפנוי שנוצר בקליפה מתמלא כאשר אלקטרון ברמה גבוהה יותר יורד לרמה המכילה את החלל הפנוי, ופולט פוטון בתהליך. בדרך כלל, האנרגיה של מעברים כאלה היא גדולה מ- ולפוטוני קרני הרנטגן הנפלטים יש אורכי גל בטווח של עד . קיומם של קווים אופייניים בספקטרום קרני רנטגן הוא עדות ישירה נוספת לקוונטיזציה של אנרגיה במערכות אטומיות.

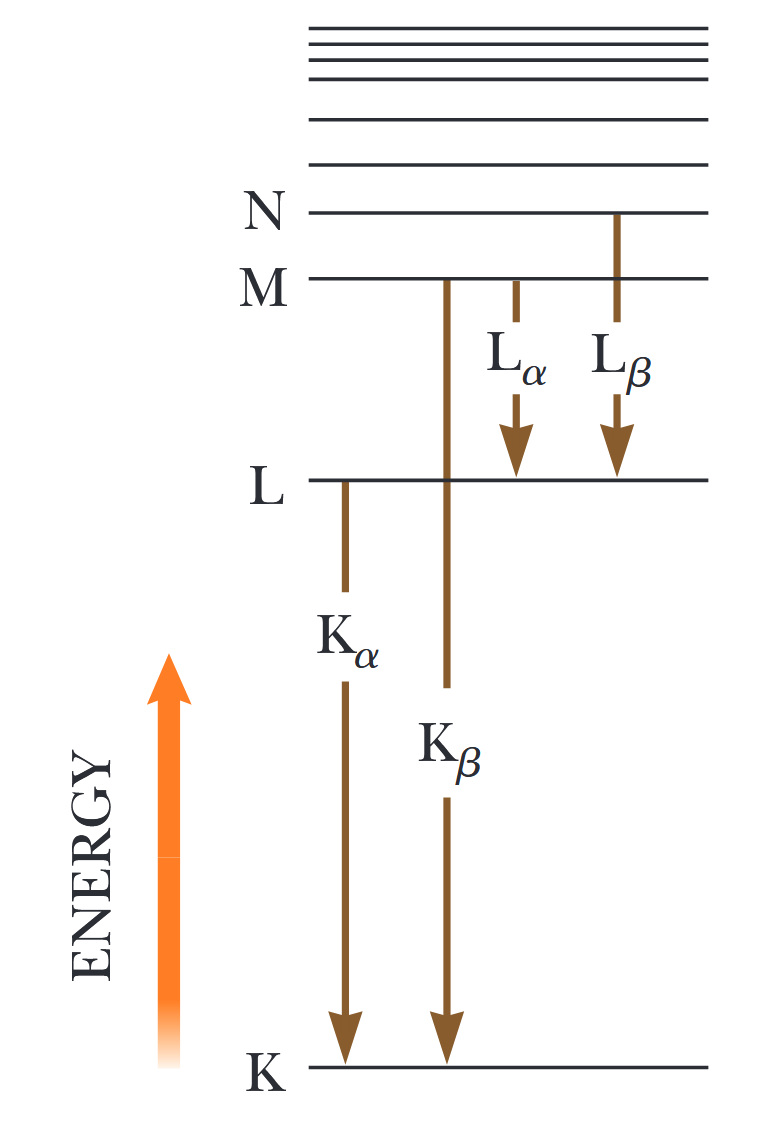
מעברים בין רמות אנרגיה אטומיות גבוהות ונמוכות המביאים לפוטוני קרני רנטגן מאטומים כבדים כאשר הם מופגזים באלקטרונים בעלי אנרגיה גבוהה. (Serway et al., 2019).

בואו נניח שהאלקטרון הנכנס עקר אלקטרון אטומי מהקליפה הפנימית ביותר, קליפת . אם החלל הפנוי מתמלא על ידי אלקטרון היורד מהקליפה הגבוהה הבאה - קליפת - לפוטון הנפלט יש אנרגיה המתאימה לקו קרני הרנטגן האופייני בעקומה של איור 6.9. בסימון זה, מתייחס לרמה הסופית של האלקטרון והאינדקס , כאות הראשונה של האלפבית היווני, מתייחס לרמה הראשונית כראשונה מעל הרמה הסופית. אם החלל הפנוי בקליפת מתמלא על ידי אלקטרון היורד מקליפת , נוצר קו . קווי קרני רנטגן אופייניים אחרים נוצרים כאשר אלקטרונים יורדים מרמות עליונות לחללים פנויים שאינם אלה בקליפת . לדוגמה, קווי מיוצרים כאשר חללים פנויים בקליפת מתמלאים על ידי אלקטרונים היורדים מקליפות גבוהות יותר. קו מיוצר כאשר אלקטרון יורד מקליפת לקליפת , וקו מיוצר על ידי מעבר מקליפת לקליפת .

למרות שלא ניתן לנתח אטומים רב-אלקטרוניים במדויק עם מודל בוהר או משוואת שרדינגר, אנו יכולים ליישם את חוק גאוס כדי לבצע כמה הערכות מדויקות באופן מפתיע של אנרגיות קרני רנטגן ואורכי גל צפויים. נניח וישנו אטום בעל מספר אטומי שבו אחד משני האלקטרונים בקליפת נפלט. דמיינו ציור משטח גאוסיאני בתוך הרדיוס הסביר ביותר של אלקטרוני . השדה החשמלי במיקום אלקטרוני הוא שילוב של השדות שנוצרו על ידי הגרעין, אלקטרון היחיד, שאר אלקטרוני והאלקטרונים החיצוניים. פונקציות הגל של האלקטרונים החיצוניים הן כאלה שלאלקטרונים יש הסתברות גבוהה מאוד להיות רחוקים יותר מהגרעין ממה שאלקטרוני נמצאים. לכן, האלקטרונים החיצוניים נוטים להיות מחוץ למשטח הגאוסיאני יותר מבפנים, ובממוצע אינם תורמים באופן משמעותי לשדה החשמלי במיקום אלקטרוני . המטען האפקטיבי בתוך המשטח הגאוסיאני הוא המטען הגרעיני החיובי ומטען שלילי אחד בשל אלקטרון היחיד. אם מתעלמים מהאינטראקציות בין אלקטרוני , אלקטרון יחיד מתנהג כאילו הוא חווה שדה חשמלי עקב מטען התחום במשטח הגאוסיאני. המטען הגרעיני מוסתר על ידי האלקטרון בקליפת כך ש- במשוואה (SJ41.36) הוא . עבור קליפות ברמה גבוהה יותר, המטען הגרעיני מוסתר על ידי אלקטרונים בכל הקליפות הפנימיות.

כעת נוכל להשתמש במשוואה (SJ41.36) כדי להעריך את האנרגיה המשויכת לאלקטרון בקליפת :

לאחר שהאטום עושה את המעבר, יש שני אלקטרונים בקליפת . נוכל לקרב את האנרגיה המשויכת לאחד מאלקטרונים אלה לזו של אטום חד-אלקטרוני. (במציאות, המטען הגרעיני מופחת במקצת על ידי המטען השלילי של האלקטרון האחר, אך בואו נתעלם מהשפעה זו.) לפיכך,

כפי שהדוגמה הבאה מראה, ניתן להעריך את האנרגיה של האטום עם אלקטרון בקליפת באופן דומה. על ידי לקיחת הפרש האנרגיה בין הרמות הראשונית והסופית, נוכל אז לחשב את האנרגיה ואורך הגל של הפוטון הנפלט.

בשנת 1914, הנרי ג’. י’. מוזלי (1887-1915) שרטט את מול ערכי עבור מספר יסודות, כאשר הוא אורך הגל של קו של כל יסוד. הוא גילה שהשרטוט הוא קו ישר כמו באיור 6.11, שעולה בקנה אחד עם חישובים גסים של רמות האנרגיה הניתנות על ידי משוואה (SJ41.37). מהשרטוט הזה, מוזלי קבע את ערכי של יסודות שטרם התגלו וייצר טבלה מחזורית בהתאמה מצוינת לתכונות הכימיות הידועות של היסודות. עד לניסוי זה, המספרים האטומיים היו רק מצייני מיקום עבור היסודות שהופיעו בטבלה המחזורית, כאשר היסודות סודרו על פי המסה.

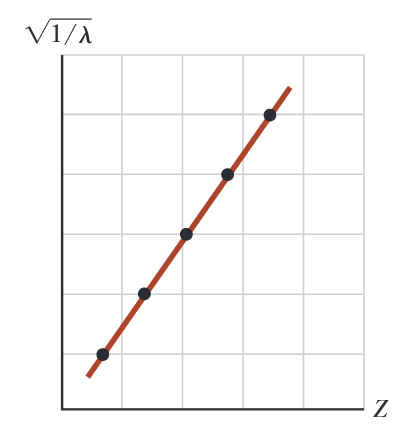
שרטוט מוזלי של מול , כאשר הוא אורך הגל של קו קרני הרנטגן של היסוד בעל המספר האטומי . (Serway et al., 2019).

דוגמה: הערכת האנרגיה של קרן רנטגן

העריכו את האנרגיה של קרן הרנטגן האופיינית הנפלטת ממטרת טונגסטן כאשר אלקטרון יורד מקליפת (מצב ) לחלל פנוי בקליפת (מצב ). המספר האטומי עבור טונגסטן הוא .

פתרון:

דמיינו אלקטרון מואץ פוגע באטום טונגסטן ומוציא אלקטרון מקליפת (). לאחר מכן, אלקטרון בקליפת () יורד כדי למלא את החלל הפנוי והפרש האנרגיה בין המצבים נפלט כפוטון קרן רנטגן.

נשתמש במשוואה (SJ41.37) ו- עבור טונגסטן כדי להעריך את האנרגיה המשויכת לאלקטרון בקליפת :

נשתמש במשוואה (SJ41.36) ובכך ש- אלקטרונים מסננים את המטען הגרעיני ( אלקטרונים במצב ואלקטרון אחד במצב ) כדי להעריך את האנרגיה של קליפת :

נמצא את האנרגיה של פוטון קרן הרנטגן הנפלט:

עיון בטבלאות קרני רנטגן מראה שאנרגיות המעבר - בטונגסטן משתנות מ- עד , כאשר טווח האנרגיות נובע מערכי אנרגיה שונים במעט עבור מצבים של שונה. לכן, ההערכה שלנו שונה מנקודת האמצע של טווח זה שנמדד ניסויית בכ-.

מעברים ספונטניים ומגורים

ראינו שאטום קולט ופולט קרינה אלקטרומגנטית רק בתדירויות המתאימות להפרשי האנרגיה בין מצבים מותרים. כעת בואו נבחן פרטים נוספים של תהליכים אלה. נניח ולאטום יש רמות אנרגיה מותרות המסומנות . כאשר קרינה פוגעת באטום, רק אותם פוטונים שהאנרגיה שלהם מתאימה להפרש האנרגיה בין שתי רמות אנרגיה יכולים להיקלט על ידי האטום כפי שמיוצג באיור. תהליך זה נקרא בליעה מגורה מכיוון שהפוטון מגרה את האטום לבצע מעבר כלפי מעלה. בטמפרטורות רגילות, רוב האטומים נמצאים במצב היסוד. אם כלי המכיל אטומים רבים של יסוד גזי מואר בקרינה של כל התדירויות האפשריות של פוטונים (כלומר, ספקטרום רציף), רק אותם פוטונים בעלי האנרגיה , , , וכן הלאה נקלטים על ידי האטומים. כתוצאה מבליעה זו, חלק מהאטומים מועלים למצבים מעוררים.

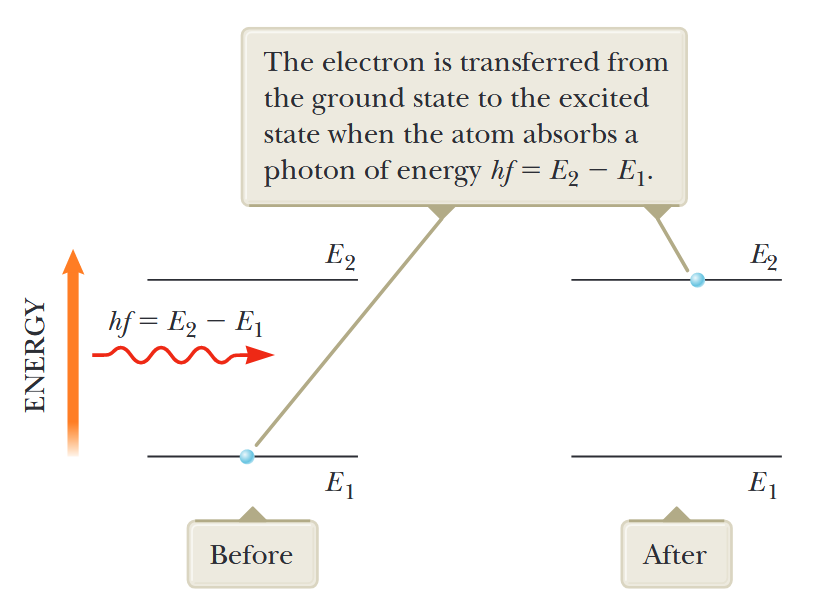
בליעה מגורה של פוטון. האלקטרון עובר ממצב היסוד למצב המעורר כאשר האטום קולט פוטון באנרגיה . (Serway et al., 2019).

ברגע שאטום נמצא במצב מעורר, האטום המעורר יכול לבצע מעבר חזרה לרמת אנרגיה נמוכה יותר, ונפלט פוטון כפי שמוצג באיור 6.12. תהליך זה ידוע כפליטה ספונטנית מכיוון שהוא מתרחש באופן טבעי, מבלי לדרוש אירוע שיפעיל את המעבר. בדרך כלל, אטום נשאר במצב מעורר רק כ-.

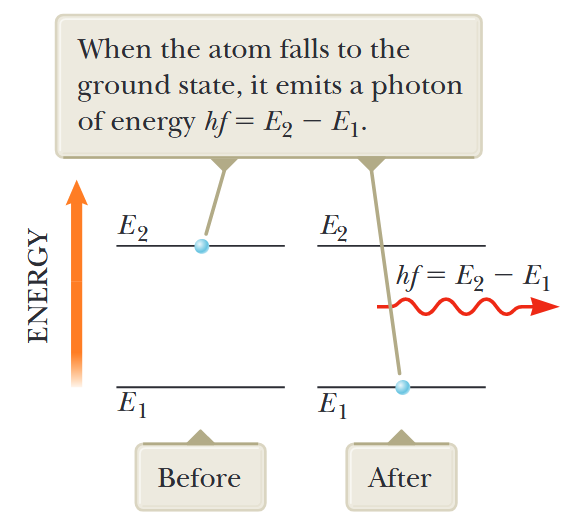
פליטה ספונטנית של פוטון על ידי אטום שנמצא בתחילה במצב המעורר . כאשר האטום יורד למצב היסוד, הוא פולט פוטון באנרגיה . (Serway et al., 2019).

בנוסף לפליטה ספונטנית, מתרחשת פליטה מגורה. נניח שאטום נמצא במצב מעורר כמו באיור 6.13. אם המצב המעורר הוא מצב מטה-יציב - כלומר, אם זמן החיים שלו הוא הרבה יותר ארוך מזמן החיים הטיפוסי של של מצבים מעוררים - מרווח הזמן עד להתרחשות פליטה ספונטנית הוא ארוך יחסית. בואו נדמיין שבמהלך מרווח זה פוטון באנרגיה פוגע באטום. אפשרות אחת היא שאנרגיית הפוטון מספיקה עבור הפוטון ליינן את האטום. אפשרות נוספת היא שהאינטראקציה בין הפוטון הנכנס והאטום גורמת לאטום לחזור למצב היסוד ולפלוט בכך פוטון שני באנרגיה . בתהליך זה, הפוטון הפוגע אינו נבלע; לכן, לאחר הפליטה המגורה, שני פוטונים באנרגיה זהה קיימים: הפוטון הפוגע והפוטון הנפלט. השניים נמצאים בפאזה ונוסעים באותו כיוון, שזהו שיקול חשוב בלייזרים.

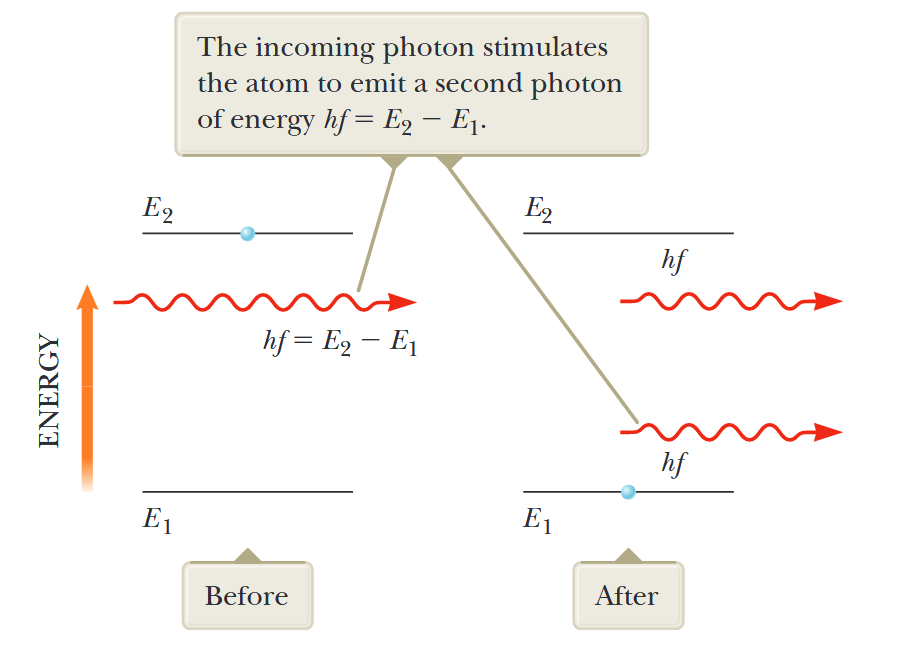
פליטה מגורה של פוטון על ידי פוטון נכנס באנרגיה . בתחילה, האטום נמצא במצב המעורר. הפוטון הנכנס מגרה את האטום לפלוט פוטון שני באנרגיה . (Serway et al., 2019).

הערה:

תופעה זו נובעת ביסודה מתהודה. לפוטון הנכנס יש תדירות ומניע את מערכת האטום באותה תדירות. מכיוון שתדירות ההנעה תואמת לזו המשויכת למעבר בין מצבים - אחת מהתדירויות הטבעיות של האטום - יש תגובה גדולה: האטום מבצע את המעבר.

לייזרים

בחלק זה, נחקור את טבע אור הלייזר ומגוון יישומים של לייזרים בחברה הטכנולוגית שלנו. התכונות העיקריות של אור לייזר שהופכות אותו לשימושי ביישומים טכנולוגיים אלה הן:

• אור לייזר קוהרנטי. הקרניים הבודדות של אור באלומת לייזר שומרות על יחס פאזה קבוע זו עם זו.
• אור לייזר מונוכרומטי. לאור באלומת לייזר יש טווח צר מאוד של אורכי גל.
• לאור לייזר יש זווית הסתעפות קטנה. האלומה מתפזרת מעט מאוד, אפילו על פני מרחקים גדולים.

כדי להבין את מקור התכונות הללו, בואו נשלב את הידע שלנו על רמות אנרגיה אטומיות מפרק זה עם כמה דרישות מיוחדות עבור האטומים הפולטים לייזר. תיארנו כיצד פוטון פוגע יכול לגרום למעברי אנרגיה אטומיים כלפי מעלה (בליעה מגורה) או כלפי מטה (פליטה מגורה). שני התהליכים בעלי הסתברות שווה. כאשר אור פוגע באוסף של אטומים, בדרך כלל מתרחשת בליעה נטו של אנרגיה מכיוון שכאשר המערכת נמצאת בשיווי משקל תרמי, אטומים רבים יותר נמצאים במצב היסוד מאשר במצבים מעוררים. עם זאת, אם המצב יכול להתהפך כך שאטומים רבים יותר נמצאים במצב מעורר מאשר במצב היסוד, פליטה נטו של פוטונים יכולה להתרחש. מצב כזה נקרא היפוך אוכלוסייה.

היפוך אוכלוסייה הוא, למעשה, העיקרון הבסיסי המעורב בפעולה של לייזר (ראשי תיבות של light amplification by stimulated emission of radiation - הגברת אור על ידי פליטה מגורה של קרינה). השם המלא מציין את אחת הדרישות עבור אור לייזר: כדי להשיג פעולת לייזר, התהליך של פליטה מגורה חייב להתרחש. הביטו בשני הפוטונים הנוסעים בחומר לאחר הפליטה המגורה שנדונה באיור 6.13. פוטונים אלה יכולים לגרות אטומים אחרים לפלוט פוטונים בשרשרת של תהליכים דומים. הפוטונים הרבים המיוצרים באופן זה הם המקור של האור האינטנסיבי והקוהרנטי בלייזר.

כדי שהפליטה המגורה תביא לאור לייזר, חייבת להיות הצטברות של פוטונים במערכת. שלושת התנאים הבאים חייבים להתמלא כדי להשיג הצטברות זו:

1. המערכת חייבת להיות במצב של היפוך אוכלוסייה: חייבים להיות יותר אטומים במצב מעורר מאשר במצב היסוד. זה חייב להיות נכון מכיוון שמספר הפוטונים הנפלטים חייב להיות גדול יותר ממספר הנבלעים.

2. המצב המעורר של המערכת חייב להיות מצב מטה-יציב, כלומר זמן החיים שלו חייב להיות ארוך בהשוואה לזמני החיים הקצרים בדרך כלל של מצבים מעוררים, שהם בדרך כלל . במקרה זה, ניתן לבסס את היפוך האוכלוסייה ופליטה מגורה צפויה להתרחש לפני פליטה ספונטנית.

3. הפוטונים הנפלטים חייבים להיות מוגבלים במערכת מספיק זמן כדי לאפשר להם לגרות פליטה נוספת מאטומים מעוררים אחרים. זה מושג על ידי שימוש במראות מחזירות בקצוות המערכת. קצה אחד עשוי מחזיר לחלוטין, והשני מחזיר חלקית. חלק מעוצמת האור עוברת דרך הקצה המחזיר חלקית, ויוצרת את אלומת אור הלייזר (איור 6.14).

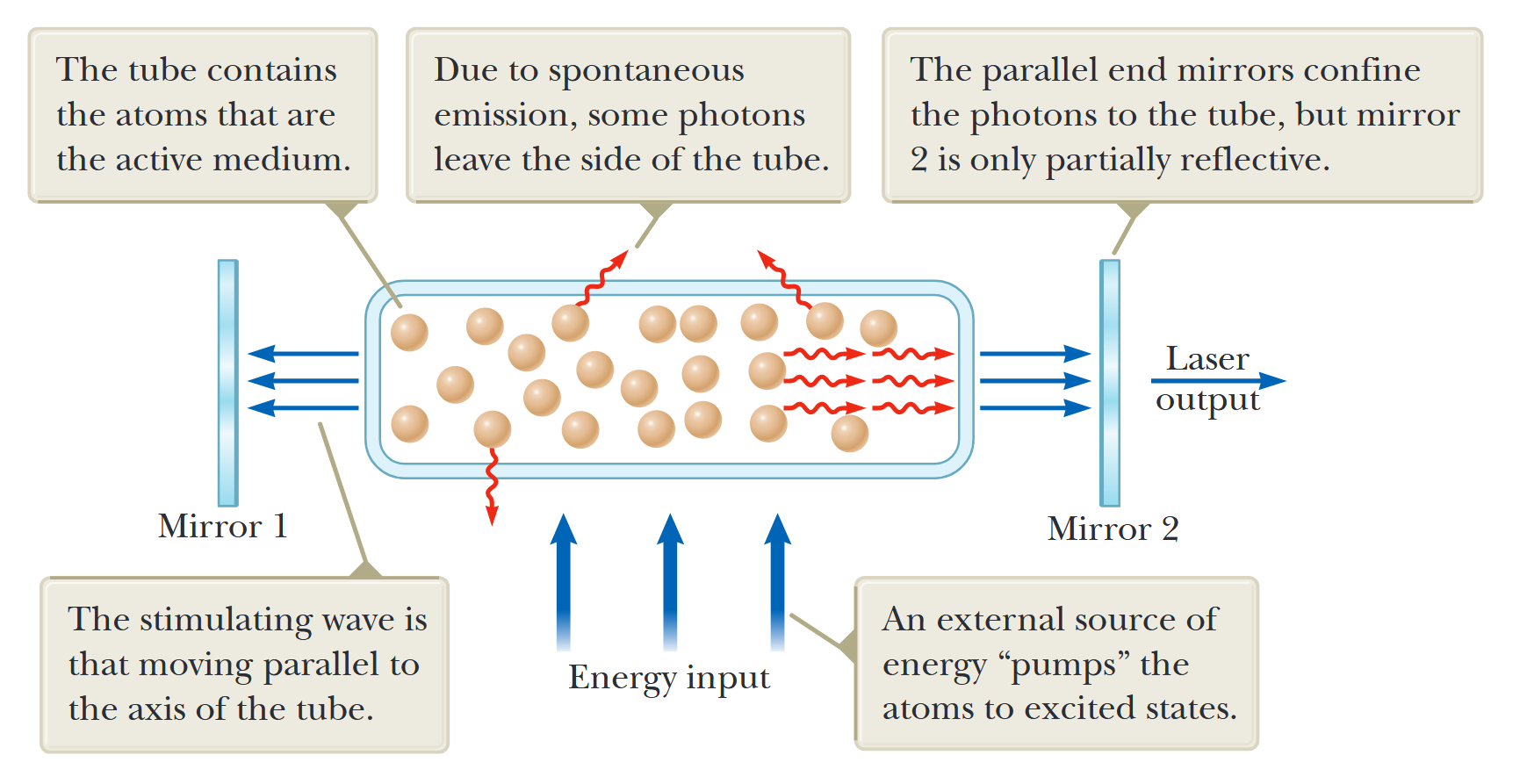
דיאגרמה סכמטית של לייזר. הצינור מכיל את האטומים שהם המדיום הפעיל. מקור חיצוני של אנרגיה “שואב” את האטומים למצבים מעוררים. המראות המקבילות בקצוות מגבילות את הפוטונים לצינור, אך מראה 2 מחזירה רק חלקית. הגל המגרה הוא זה הנע במקביל לציר הצינור. בשל פליטה ספונטנית, כמה פוטונים יוצאים מצד הצינור. (Serway et al., 2019).

התקן אחד שמציג פליטה מגורה של קרינה הוא לייזר הגז הליום-נאון. איור 6.15 הוא דיאגרמת רמות אנרגיה עבור אטום הנאון במערכת זו. התערובת של הליום ונאון מוגבלת לצינור זכוכית שאטום בקצוותיו על ידי מראות. מתח המופעל על פני הצינור גורם לאלקטרונים לזרום דרך הצינור, להתנגש עם אטומי הגזים ולהעלות אותם למצבים מעוררים. אטומי נאון מתרגשים למצב דרך תהליך זה (הכוכבית מציינת מצב מטה-יציב) וכן כתוצאה מהתנגשויות עם אטומי הליום הם מעוררים. לפיכך, מתרחשת פליטה מגורה, הגורמת לאטומי נאון לבצע מעברים למצב . אטומים מעוררים שכנים גם מגורים. התוצאה היא ייצור אור קוהרנטי באורך גל של .

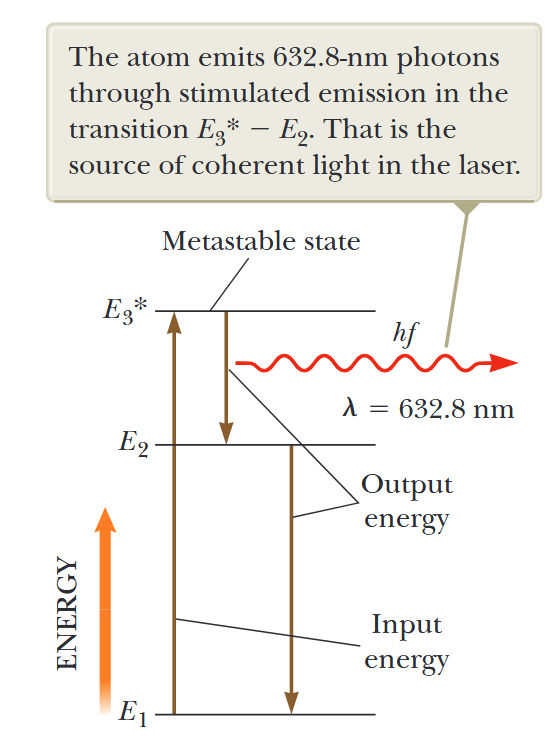
דיאגרמת רמות אנרגיה עבור אטום נאון בלייזר הליום-נאון. האטום פולט פוטונים של דרך פליטה מגורה במעבר . זה המקור של האור הקוהרנטי בלייזר. (Serway et al., 2019).

הערות שוליים

1. בקירוב ראשון, האנרגיה תלויה רק במספר הקוונטי , כפי שדיברנו עליו. בגלל השפעת המטען האלקטרוני שמסנן את המטען הגרעיני, עם זאת, האנרגיה תלויה גם ב- באטומים רב-אלקטרוניים. ↩

→ קודם: PHY3_005הבא: PHY3_007 ←