PHY3_007 מולקולות ומוצקים

→ קודם: PHY3_006הבא: PHY3_008 ←

גבישים

מוצק גבישי מורכב ממספר גדול של אטומים המסודרים במערך סדיר, היוצר מבנה מחזורי. היונים בגביש קשורים קשר יוני ואטומי הפחמן ביהלום יוצרים קשרים קוולנטיים זה עם זה. הקשר המתכתי המתואר בסוף חלק זה אחראי לגבישיות של נחושת, כסף, נתרן ומתכות מוצקות אחרות.

מוצקים יוניים

גבישים רבים נוצרים על ידי קישור יוני, שבו האינטראקציה הדומיננטית בין יונים היא כוח קולון. הביטו בחלק מגביש המוצג באיור 7.1. הכדורים האדומים הם יוני נתרן, והכדורים הכחולים הם יוני כלור. כפי שמוצג באיור, לכל יון יש שישה יוני שכנים. באופן דומה, אנו רואים שלכל יון יש שישה יוני שכנים. כל יון נמשך לששת שכניו . האנרגיה הפוטנציאלית המתאימה היא , כאשר הוא קבוע קולון ו- הוא מרחק ההפרדה בין כל ו-. בנוסף, יש יוני שכנים-הבאים-בקרבה במרחק מיון , ו- היונים החיוביים הללו מפעילים כוחות דחייה חלשים יותר על ה- המרכזי. יתר על כן, מעבר ל- יוני הללו יש עוד יוני שמפעילים כוח משיכה, וכן הלאה. ההשפעה הכללית של כל האינטראקציות הללו היא אנרגיה פוטנציאלית חשמלית שלילית:

כאשר הוא מספר חסר ממדים הידוע כקבוע מדלונג (Madelung constant). הערך של תלוי רק במבנה הגבישי הספציפי של המוצק. לדוגמה, עבור מבנה .

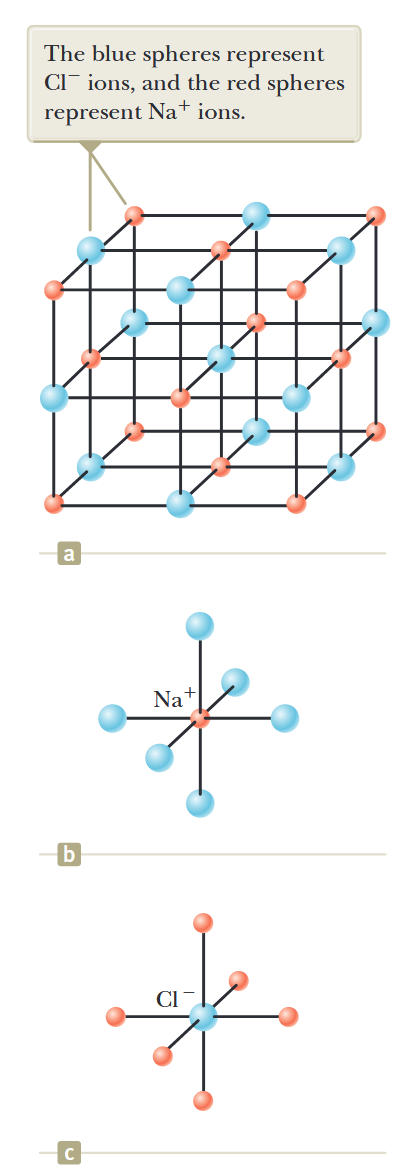
איור 7.1: מבנה גבישי של . (a) הכדורים הכחולים מייצגים יוני , והכדורים האדומים מייצגים יוני . (b) כל יון נתרן חיובי מוקף בשישה יוני כלור שליליים. (c) כל יון כלור מוקף בשישה יוני נתרן. (Serway et al., 2019).

גבישים יוניים יוצרים גבישים יציבים וקשים יחסית. הם מוליכים חשמליים גרועים מכיוון שהם אינם מכילים אלקטרונים חופשיים; כל אלקטרון במוצק קשור בחוזקה לאחד היונים, כך שהוא אינו נייד מספיק כדי לשאת זרם. לגבישים יוניים יש נקודות התכה גבוהות; לדוגמה, נקודת ההתכה של היא . גבישים יוניים שקופים לקרינה נראית מכיוון שהקליפות שנוצרות על ידי האלקטרונים במוצקים יוניים קשורות כל כך חזק שלקרינה נראית אין אנרגיה מספקת להעלות אלקטרונים לקליפה המותרת הבאה. קרינה אינפרה-אדומה נבלעת בחוזקה מכיוון שלרעידות של היונים יש תדירויות תהודה טבעיות באזור האינפרה-אדום בעל האנרגיה הנמוכה.

מוצקים קוולנטיים

פחמן מוצק, בצורת יהלום, הוא גביש שאטומיו קשורים קשר קוולנטי. מכיוון שלפחמן אטומי יש התצורה האלקטרונית , הוא חסר ארבעה אלקטרונים כדי למלא את הקליפה שלו, שיכולה להכיל שמונה אלקטרונים. בגלל מבנה אלקטרוני זה, לשני אטומי פחמן יש משיכה חזקה זה לזה. במבנה היהלום, כל אטום פחמן קשור קשר קוולנטי לארבעה אטומי פחמן אחרים הממוקמים בארבע פינות של קובייה כפי שמוצג באיור 7.2. שימו לב שכל אטום פחמן יוצר קשרים קוולנטיים עם ארבעה אטומים שכנים הקרובים ביותר. המבנה הבסיסי של יהלום נקרא טטרהדרלי (כל אטום פחמן נמצא במרכז טטרהדרון סדיר), והזווית בין הקשרים היא . לגבישים אחרים כמו סיליקון וגרמניום יש את אותו המבנה.

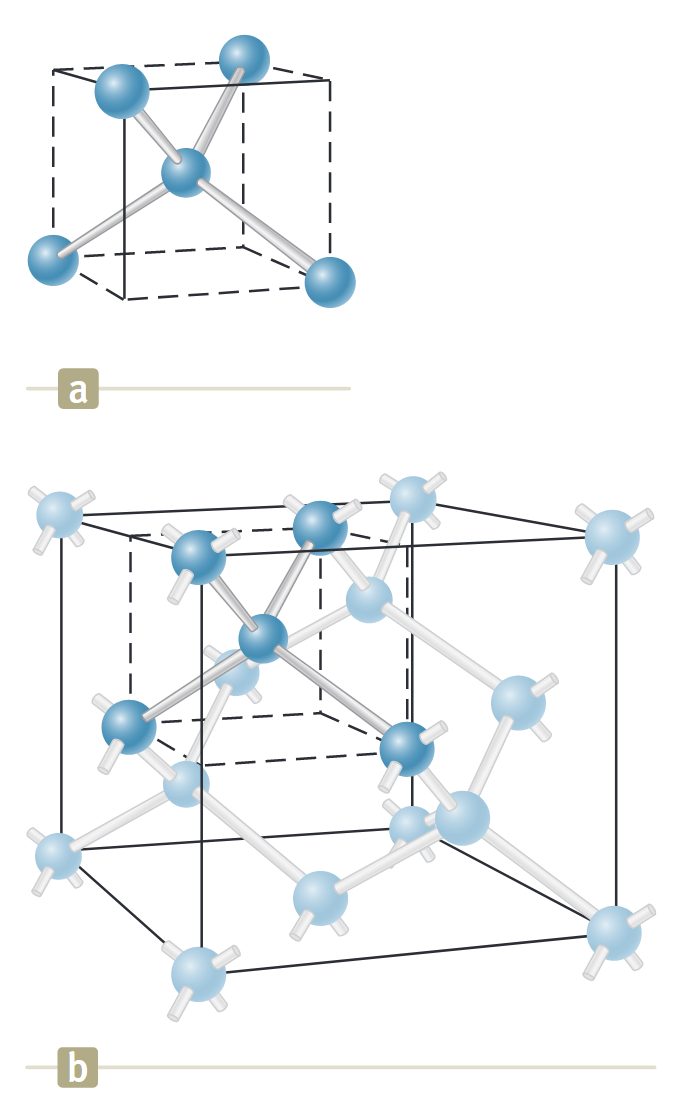
איור 7.2: מבנה יהלום. (a) כל אטום פחמן בגביש יהלום קשור קשר קוולנטי לארבעה אטומי פחמן אחרים כך שנוצר מבנה טטרהדרלי. (b) המבנה הגבישי של יהלום, המראה את סידור הקשרים הטטרהדרליים. (Serway et al., 2019).

פחמן מעניין בכך שהוא יכול ליצור כמה סוגים שונים של מבנים. בנוסף למבנה היהלום, הוא יוצר גרפיט, עם תכונות שונות לחלוטין. בצורה זו, אטומי הפחמן יוצרים שכבות שטוחות עם מערכים משושיים של אטומים. אינטראקציה חלשה מאוד בין השכבות מאפשרת להסיר את השכבות בקלות תחת חיכוך, כפי שמתרחש בגרפיט המשמש בעיפרון. אטומי פחמן יכולים גם ליצור מבנה חלול גדול; במקרה זה, התרכובת נקראת בקמינסטרפולרן על שם האדריכל הידוע ר. בקמינסטר פולר, שהמציא את הכיפה הגיאודזית. הצורה הייחודית של מולקולה זו (איור 7.3) מספקת “כלוב” להחזיק אטומים או מולקולות אחרים. מבנים קשורים, הנקראים “בקיטיובים” בגלל הסידורים הגליליים הארוכים והצרים שלהם של אטומי פחמן, עשויים לספק את הבסיס לחומרים חזקים ביותר, אך קלי משקל.

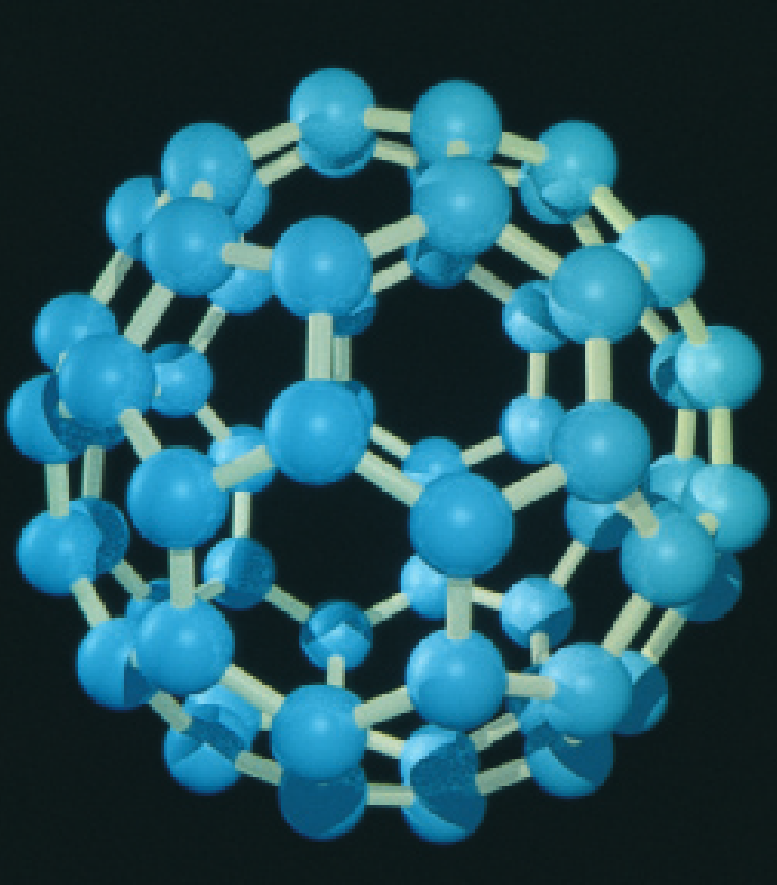
איור 7.3: עיבוד מחשב של “בקיבול”, קיצור למולקולה בקמינסטרפולרן. מבנים מולקולריים כדוריים כמעט אלה שנראים כמו כדורי כדורגל נקראו על שם ממציא הכיפה הגיאודזית. צורה זו של פחמן, , התגלתה על ידי אסטרופיזיקאים שחקרו את גז הפחמן הקיים בין כוכבים. (Serway et al., 2019).

מוצקים מתכתיים

קשרים מתכתיים הם בדרך כלל חלשים יותר מקשרים יוניים או קוולנטיים. האלקטרונים החיצוניים באטומי מתכת חופשיים יחסית לנוע בכל החומר, ומספר האלקטרונים הניידים הללו במתכת גדול. ניתן לראות את המבנה המתכתי כ”ים” או “גז” של אלקטרונים כמעט חופשיים המקיפים סריג של יונים חיוביים (איור 7.4). מנגנון הקישור במתכת הוא כוח המשיכה בין כל האוסף של יונים חיוביים לבין גז האלקטרונים.

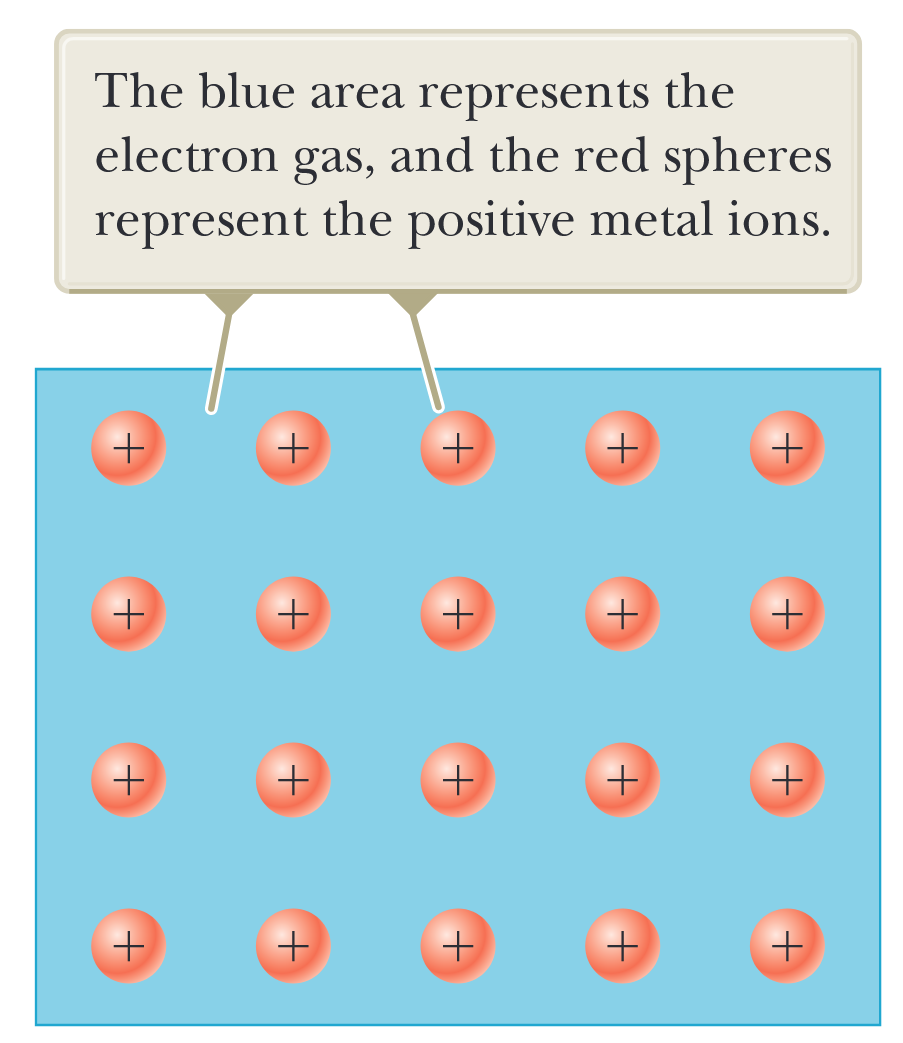
איור 7.4: דיאגרמה סכמטית ביותר של מתכת. האזור הכחול מייצג את גז האלקטרונים, והכדורים האדומים מייצגים את יוני המתכת החיוביים. (Serway et al., 2019).

אור מקיים אינטראקציה חזקה עם האלקטרונים החופשיים במתכות. לכן, אור נראה נבלע ונפלט מחדש די קרוב לפני השטח של מתכת, מה שמסביר את הטבע המבריק של משטחי מתכת. בנוסף למוליכות החשמלית הגבוהה של מתכות המיוצרת על ידי האלקטרונים החופשיים, הטבע הלא-כיווני של הקשר המתכתי מאפשר לסוגים שונים רבים של אטומי מתכת להתמוסס במתכת אחרת בכמויות משתנות. ניתן ליצור תמיסות מוצקות או סגסוגות (פלדה, ברונזה, פליז וכו’) ולתכנן אותן כך שיהיו בעלות תכונות מסוימות, כמו חוזק מתיחה, ניתנות לעיבוד, מוליכות חשמלית ותרמית ועמידות בפני קורוזיה.

מוצקים לא-מתכתיים נוטים להישבר כאשר הם מועמדים ללחץ. שבירה נובעת מכך שקישור במוצקים לא-מתכתיים הוא בעיקר עם יונים או אטומים שכנים הקרובים ביותר. כאשר העיוות גורם ללחץ מספק בין קבוצה כלשהי של שכנים הקרובים ביותר, מתרחשת שבירה. לעומת זאת, מתכות נוטות להתכופף כאשר הן מועמדות ללחץ. הקישור במתכות הוא בין כל האלקטרונים וכל היונים החיוביים. לכן, אין קשר מקומי שנשבר כאשר המתכת מתכופפת.

תיאוריית האלקטרונים החופשיים במתכות

בפיזיקה 2 תיארנו תיאוריית אלקטרונים חופשיים קלאסית של הולכה חשמלית במתכות, מודל מבני שהוביל לחוק אום. על פי תיאוריה זו, מתכת ממודלת כגז קלאסי של אלקטרוני הולכה הנעים דרך סריג קבוע של יונים. למרות שתיאוריה זו צופה את הצורה הפונקציונלית הנכונה של חוק אום, היא אינה צופה את הערכים הנכונים של מוליכות חשמלית ותרמית. תיאוריית אלקטרונים חופשיים מבוססת קוונטים של מתכות מתקנת את החסרונות של המודל הקלאסי על ידי התחשבות בטבע הגלי של האלקטרונים. במודל זה, המבוסס על מודל הניתוח של חלקיק קוונטי תחת תנאי שפה, אלקטרוני הקליפה החיצונית חופשיים לנוע דרך המתכת אך הם לכודים בתוך קופסה תלת-ממדית שנוצרת על ידי משטחי המתכת. לכן, כל אלקטרון מיוצג כחלקיק בקופסה. כפי שנדון, חלקיקים בקופסה מוגבלים לרמות אנרגיה מקוונטות.

ניתן ליישם פיזיקה סטטיסטית על אוסף חלקיקים במאמץ לקשר תכונות מיקרוסקופיות לתכונות מקרוסקופיות כפי שראינו עם התיאוריה הקינטית של גזים. במקרה של אלקטרונים, יש צורך להשתמש בסטטיסטיקה קוונטית, עם הדרישה שכל מצב קוונטי של המערכת יכול להיות ממולא על ידי שני אלקטרונים בלבד (אחד עם ספין למעלה והשני עם ספין למטה) כתוצאה מעקרון האיסור. ההסתברות שמצב מסוים בעל אנרגיה ממולא על ידי אחד האלקטרונים במוצק היא:

כאשר נקראת פונקציית התפלגות פרמי-דיראק ו- נקראת אנרגיית פרמי. גרף של מול ב- מוצג באיור 7.5. שימו לב ש- עבור ו- עבור . כלומר, ב-, כל המצבים בעלי אנרגיות קטנות מאנרגיית פרמי ממולאים וכל המצבים בעלי אנרגיות גדולות מאנרגיית פרמי פנויים. מצב זה עקבי עם עקרון האיסור. גרף של מול בטמפרטורה כלשהי מוצג באיור. עקומה זו מראה שככל ש- גדלה, ההתפלגות מתעגלת מעט. בגלל עירור תרמי, מצבים ליד ומתחת ל- מאבדים אוכלוסייה ומצבים ליד ומעל זוכים לאוכלוסייה. אנרגיית פרמי גם תלויה בטמפרטורה, אך התלות חלשה במתכות.

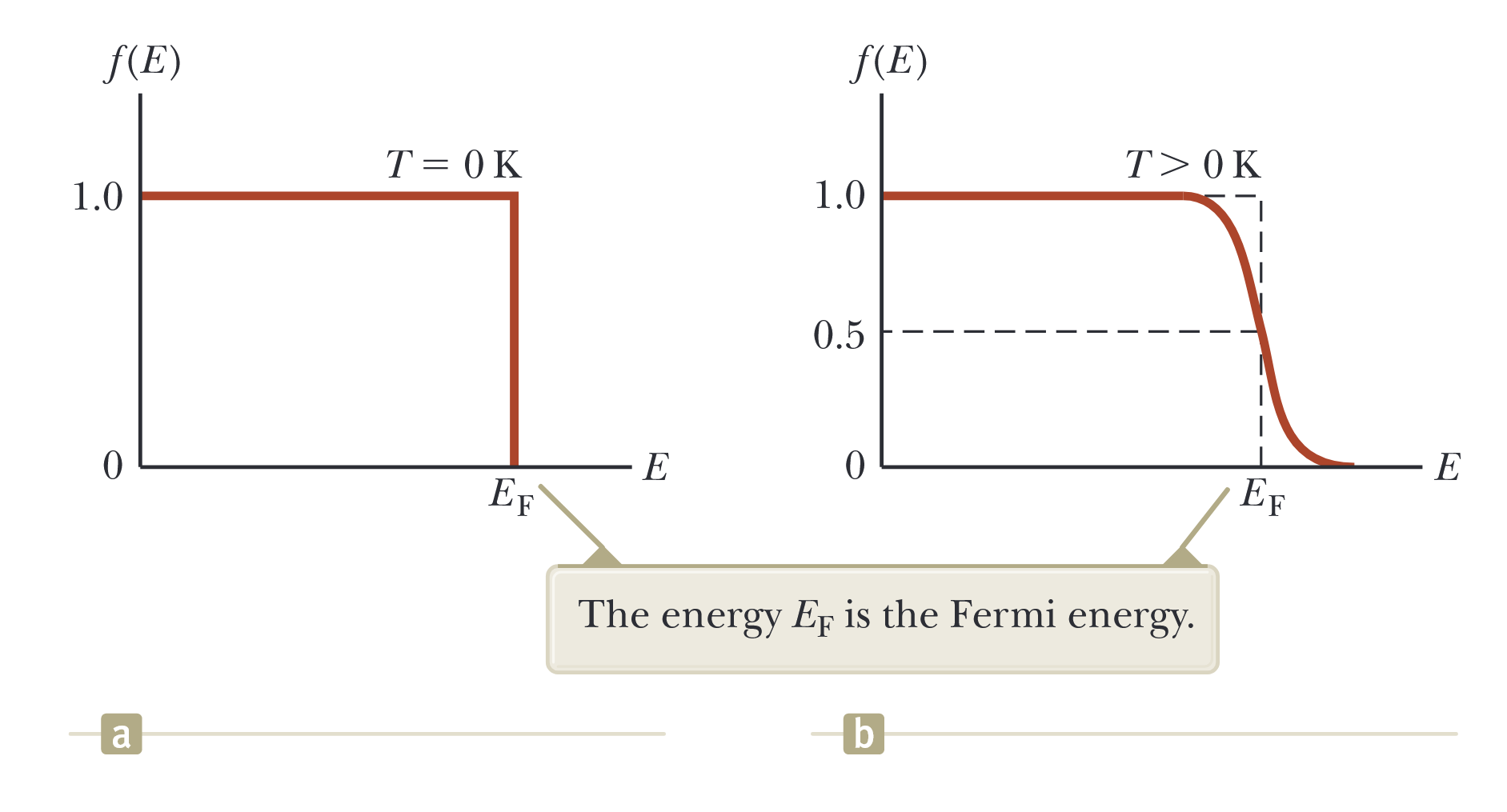
איור 7.5: גרף של פונקציית התפלגות פרמי-דיראק מול אנרגיה ב-(a) ו-(b) . האנרגיה היא אנרגיית פרמי. (Serway et al., 2019).

כעת בואו נמשיך בדיון שלנו על החלקיק בקופסה כדי להכליל את התוצאות לקופסה תלת-ממדית. זכרו שאם חלקיק מסה מוגבל לנוע בקופסה חד-ממדית באורך , למצבים המותרים יש רמות אנרגיה מקוונטות הניתנות על ידי:

כעת דמיינו חתיכת מתכת בצורת קובייה מוצקה בעלת צלעות ונפח והתמקדו באלקטרון אחד שחופשי לנוע בכל מקום בנפח זה. במודל זה, אנו דורשים ש- בגבולות המתכת. ניתן להראות שהאנרגיה עבור אלקטרון כזה היא:

כאשר היא מסת האלקטרון ו- הם מספרים קוונטיים. כפי שאנו מצפים, האנרגיות מקוונטות, וכל ערך מותר של האנרגיה מאופיין על ידי מערך זה של שלושה מספרים קוונטיים (אחד לכל דרגת חופש) והמספר הקוונטי הסיבובי . לדוגמה, למצב היסוד, המתאים ל-, יש אנרגיה השווה ל- והוא יכול להיות תפוס על ידי שני אלקטרונים, המתאימים לספין למעלה ולמטה.

בגלל הגודל המקרוסקופי של הקופסה, רמות האנרגיה עבור האלקטרונים קרובות מאוד זו לזו. כתוצאה מכך, אנו יכולים להתייחס למספרים הקוונטיים כמשתנים רציפים. תחת הנחה זו, מספר המצבים המותרים ליחידת נפח שיש להם אנרגיות בין ו- הוא:

הפונקציה נקראת פונקציית צפיפות המצבים. אם מתכת נמצאת בשיווי משקל תרמי, מספר האלקטרונים ליחידת נפח שיש להם אנרגיה בין ו- שווה למכפלה של מספר המצבים המותרים ליחידת נפח וההסתברות שמצב תפוס; כלומר, :

גרפים של מול עבור שתי טמפרטורות ניתנים באיור 7.6. אם הוא המספר הכולל של אלקטרונים ליחידת נפח, אנו דורשים ש:

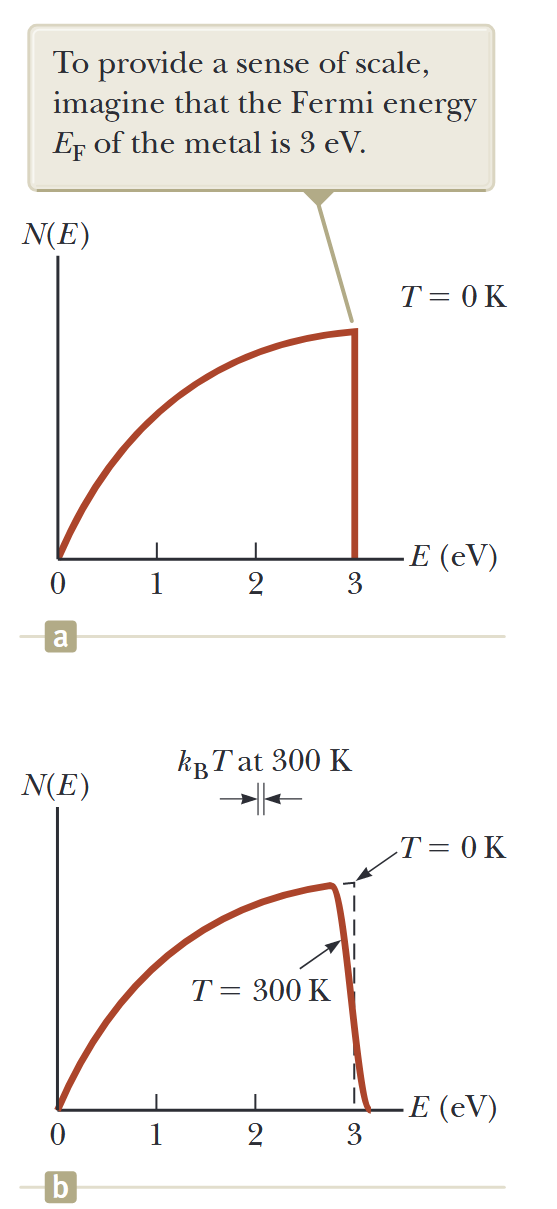
איור 7.6: גרף של פונקציית התפלגות האלקטרונים מול אנרגיה במתכת ב-(a) ו-(b) . כדי לספק תחושה של קנה מידה, דמיינו שאנרגיית פרמי של המתכת היא . (Serway et al., 2019).

אנו יכולים להשתמש בתנאי זה כדי לחשב את אנרגיית פרמי. ב-, פונקציית התפלגות פרמי-דיראק עבור ו- עבור . לכן, ב-, משוואה (SJ42.21) הופכת ל:

פתרון עבור אנרגיית פרמי ב- נותן:

אנרגיות פרמי עבור מתכות נמצאות בטווח של כמה אלקטרון וולט. ערכים מייצגים עבור מתכות שונות ניתנים בטבלה. ניתן להראות שהאנרגיה הממוצעת של אלקטרון חופשי במתכת ב- היא:

ערכים מחושבים של אנרגיית פרמי עבור מתכות ב- על בסיס תיאוריית האלקטרונים החופשיים:

מתכת	ריכוז אלקטרונים ()	אנרגיית פרמי ()

דוגמה: אנרגיית פרמי של זהב

איור 7.7: כל אטום של זהב () תורם אלקטרון חופשי אחד למתכת. חשבו את אנרגיית פרמי עבור זהב.

פתרון:

דמיינו אלקטרונים הממלאים רמות זמינות גבוהות יותר ויותר ב- בזהב. האנרגיה הגבוהה ביותר המלאה היא אנרגיית פרמי.

נציב את ריכוז האלקטרונים החופשיים בזהב מהטבלה לתוך משוואה (SJ42.23) כדי לחשב את אנרגיית פרמי ב-:

תיאוריית הפסים במוצקים

בחלק הקודם, האלקטרונים במתכת מודלו כחלקיקים החופשיים לנוע בתוך קופסה תלת-ממדית והתעלמנו מהשפעת האטומים. בחלק זה, אנו הופכים את המודל למתוחכם יותר על ידי שילוב התרומה של האטומים המקוריים היוצרים את הגביש. בהתבסס על הדיון שלנו בפרק קודם, צפיפות ההסתברות למערכת היא בעלת משמעות פיזיקלית, אך אמפליטודת ההסתברות אינה כזו. בואו נבחן כדוגמה אטום שיש לו אלקטרון יחיד מחוץ לקליפה סגורה. שתי פונקציות הגל הבאות תקפות עבור אטום כזה עם מספר אטומי :

כאשר הוא קבוע הנורמליזציה ו- היא פונקציה של שמשתנה עם הערך של המספר הקוונטי הראשי .¹ בחירה של כל אחת מפונקציות הגל הללו מובילה לאותו ערך של , כך ששתי הבחירות שקולות. עם זאת, נוצר הבדל כאשר שני אטומים מתאחדים.

אם שני אטומים זהים נמצאים רחוק מאוד זה מזה, הם אינם מקיימים אינטראקציה ורמות האנרגיה האלקטרוניות שלהם יכולות להיחשב כאלה של אטומים מבודדים. נניח ששני האטומים הם נתרן, כל אחד בעל אלקטרון בודד שנמצא במצב קוונטי מוגדר היטב. כאשר שני אטומי הנתרן מתקרבים זה לזה, פונקציות הגל שלהם מתחילות להיחפף כפי שדנו עבור קישור קוולנטי בחלק קודם. התכונות של המערכת המשולבת שונות בהתאם לכך האם שני האטומים מתאחדים עם פונקציות גל כמו באיור 7.7 (a) או האם הם מתאחדים כאשר לאחד יש פונקציית גל ולשני כמו באיור 7.7 (b). הבחירה של שני אטומים עם פונקציית גל שקולה פיזיקלית לזו עם שתי פונקציות גל חיוביות, כך שאיננו בוחנים אותה בנפרד.

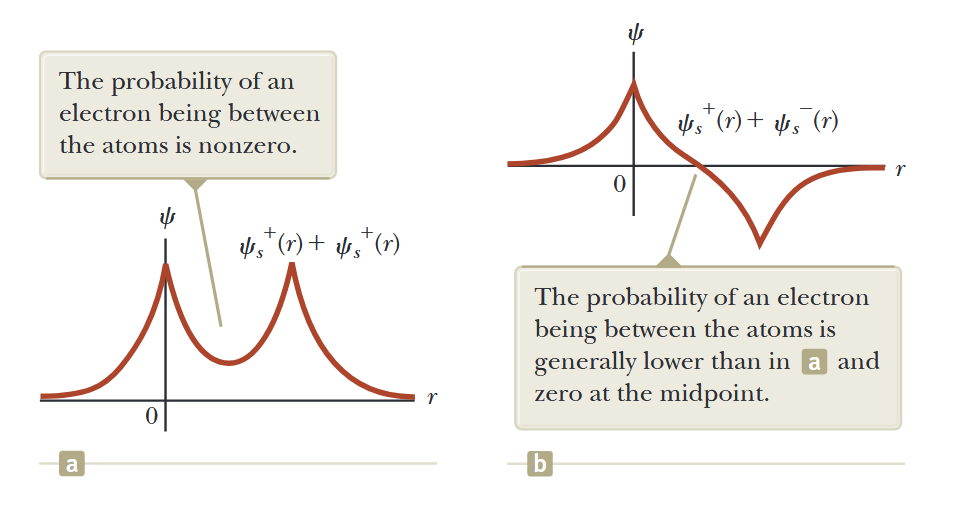
איור 7.8: פונקציות הגל של שני אטומים מתאחדות ליצור פונקציית גל משולבת למערכת של שני אטומים כאשר האטומים קרובים זה לזה. (a) שני אטומים עם פונקציות גל מתאחדים. (b) שני אטומים עם פונקציות גל ו- מתאחדים. (Serway et al., 2019).

כאשר שתי פונקציות גל מתאחדות, התוצאה היא פונקציית גל משולבת שבה אמפליטודות ההסתברות מתחברות בין האטומים. אם מתאחדת עם , עם זאת, פונקציות הגל בין הגרעינים מתחסרות. לכן, אמפליטודות ההסתברות המשולבות עבור שתי האפשרויות שונות. שני השילובים האפשריים הללו של פונקציות גל מייצגים שני מצבים אפשריים של מערכת שני האטומים.

אנו מפרשים את העקומות הללו כמייצגות את אמפליטודת ההסתברות למציאת אלקטרון. העקומה החיובית-חיובית מראה הסתברות מסוימת למציאת האלקטרון בנקודת האמצע בין האטומים. הפונקציה החיובית-שלילית אינה מראה הסתברות כזו. מצב עם הסתברות גבוהה של אלקטרון בין שני גרעינים חיוביים חייב להיות בעל אנרגיה שונה ממצב עם הסתברות גבוהה שהאלקטרון נמצא במקום אחר! לכן, המצבים מתפצלים לשתי רמות אנרגיה בגלל שתי הדרכים לשלב את פונקציות הגל. הפרש האנרגיה קטן יחסית, כך ששני המצבים קרובים זה לזה בסולם אנרגיה.

כאשר מספר גדול של אטומים מובאים יחד ליצור מוצק, מתרחשת תופעה דומה. ניתן להביא את פונקציות הגל הבודדות יחד בשילובים שונים של ו-, כל שילוב אפשרי מתאים לאנרגיה שונה. כאשר האטומים מתקרבים זה לזה, רמות האנרגיה השונות של האטום המבודד מתפצלות לרמות אנרגיה מרובות עבור המערכת המשולבת. ככל שמספר האטומים גדל, מספר השילובים של פונקציות הגל גדל, וכך גם מספר האנרגיות האפשריות.

אם אנו מרחיבים את הטיעון הזה למספר הגדול של אטומים הנמצא במוצקים (בסדר גודל של אטומים לסנטימטר מעוקב), אנו מקבלים מספר עצום של רמות אנרגיה משתנות הצמודות כל כך זו לזו שניתן להתייחס אליהן כפס רציף של רמות אנרגיה. במקרה של נתרן, נהוג להתייחס להתפלגויות הרציפות של רמות האנרגיה המותרות כפסי מכיוון שהפסים מקורם ברמות של אטומי הנתרן הבודדים. כל רמת אנרגיה באטום יכולה להתפרש לפס כאשר האטומים מתאחדים למוצק.

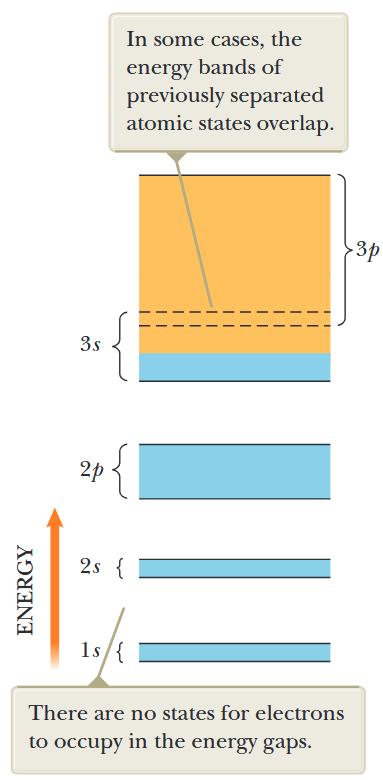
איור 7.9: פסי האנרגיה המותרים של נתרן במרחק הפרדה קבוע בין האטומים. הכחול מייצג פסי אנרגיה תפוסים על ידי אלקטרוני הנתרן כאשר האטום נמצא במצב היסוד שלו. הזהב מייצג פסי אנרגיה ריקים. (Serway et al., 2019).

איור 7.8 מראה את פסי האנרגיה המותרים של נתרן במרחק הפרדה קבוע בין האטומים. שימו לב שרווחי אנרגיה, המתאימים לאנרגיות אסורות, מתרחשים בין הפסים המותרים. בנוסף, חלק מהפסים מפגינים התפשטות מספקת באנרגיה כך שיש חפיפה בין פסים הנובעים ממצבים קוונטיים שונים ( ו-).

כפי שמצוין על ידי האזורים הצבועים בכחול באיור 7.8, פסי , ו- של נתרן מלאים כל אחד באלקטרונים מכיוון שמצבי , ו- של כל אטום מלאים. רמת אנרגיה שבה המומנט הזוויתי המסלולי הוא יכולה להכיל אלקטרונים. הגורם נובע משני כיווני הספין האפשריים של האלקטרון, והגורם מתאים למספר הכיוונים האפשריים של המומנט הזוויתי המסלולי. הקיבולת של כל פס עבור מערכת של אטומים היא אלקטרונים. לכן, פסי ו- מכילים כל אחד אלקטרונים (), ופס מכיל אלקטרונים ().

מכיוון שלנתרן יש רק אלקטרון אחד ויש סך הכל אטומים במוצק, פס מכיל רק אלקטרונים ומלא חלקית כפי שמצוין על ידי הצביעה הכחולה באיור 7.8. פס , שהוא האזור הגבוה יותר של הפסים החופפים, ריק לחלוטין (כל הזהב באיור).

תיאוריית הפסים מאפשרת לנו לבנות מודלים פשוטים להבין את ההתנהגות של מוליכים, מבודדים ומוליכים למחצה כמו גם של התקני מוליכים למחצה, כפי שנדון בחלקים הבאים.

הולכה חשמלית במתכות, מבודדים ומוליכים למחצה

מוליכים חשמליים טובים מכילים צפיפות גבוהה של נושאי מטען חופשיים, והצפיפות של נושאי מטען חופשיים במבודדים היא כמעט אפס. מוליכים למחצה הם סוג של חומרים חשובים טכנולוגית שבהם צפיפויות נושאי המטען נמצאות בין אלה של מבודדים לאלה של מוליכים. בחלק זה, אנו דנים במנגנוני ההולכה בשלושת הסוגים האלה של חומרים במונחים של מודל המבוסס על פסי אנרגיה.

מתכות

אם חומר מוליך חשמלי טוב, נושאי המטען בחומר חייבים להיות חופשיים לנוע בתגובה לשדה חשמלי מופעל. בואו נבחן את האלקטרונים במתכת כנושאי המטען. תנועת האלקטרונים בתגובה לשדה חשמלי מייצגת עלייה באנרגיה של המערכת (סריג המתכת והאלקטרונים החופשיים) המתאימה לאנרגיה הקינטית הנוספת של האלקטרונים הנעים. המערכת מתוארת על ידי מודל המערכת הלא-מבודדת עבור אנרגיה. המשוואה הופכת ל-, כאשר העבודה נעשית על האלקטרונים על ידי השדה החשמלי.

לכן, כאשר שדה חשמלי מופעל על מוליך, אלקטרונים חייבים לנוע כלפי מעלה למצב אנרגיה גבוה יותר זמין בדיאגרמת רמות אנרגיה כדי לייצג את האנרגיה הקינטית הנוספת. איור 7.9 מראה פס מלא למחצה במתכת ב-, כאשר האזור הכחול מייצג רמות מלאות באלקטרונים. מכיוון שאלקטרונים מצייתים לסטטיסטיקת פרמי-דיראק, כל הרמות מתחת לאנרגיית פרמי מלאות באלקטרונים וכל הרמות מעל אנרגיית פרמי ריקות. אנרגיית פרמי נמצאת בפס במצב המלא הגבוה ביותר.

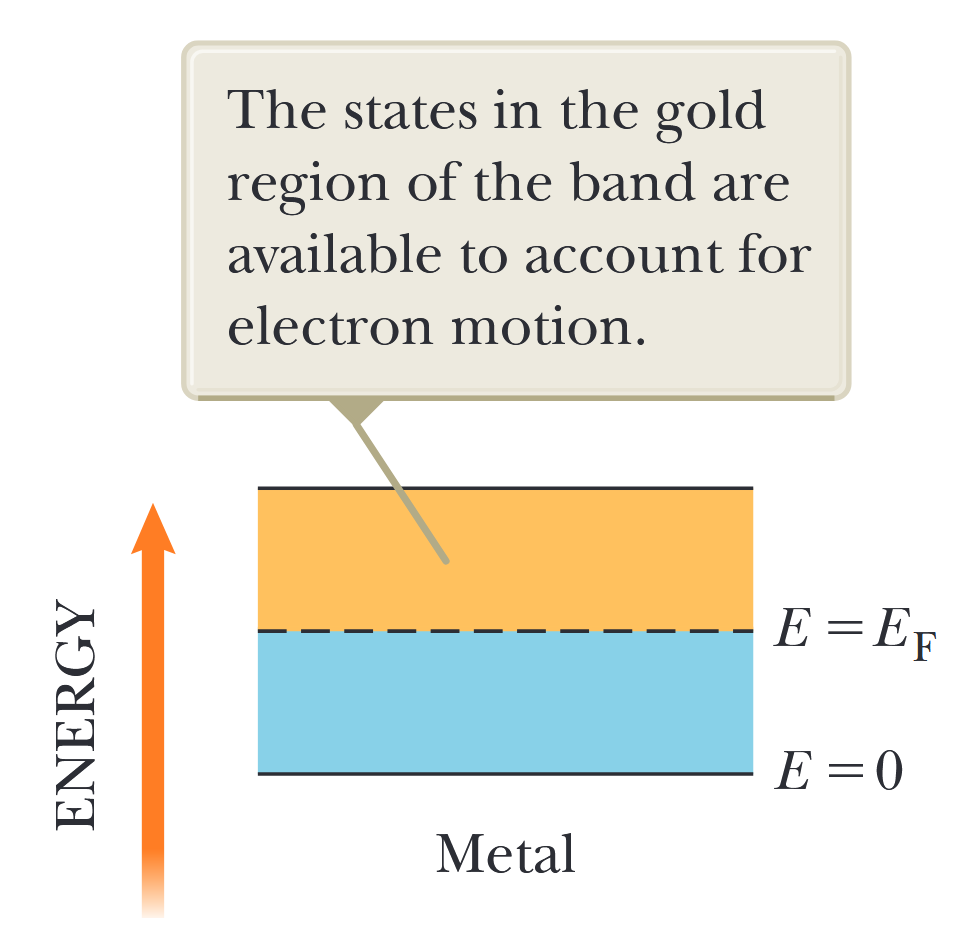
איור 7.10: פס מלא למחצה של מתכת, מוליך חשמלי. ב-, אנרגיית פרמי נמצאת באמצע הפס. המצבים באזור הזהב של הפס זמינים לתנועת אלקטרונים. (Serway et al., 2019).

בטמפרטורות קצת גבוהות מ-, חלק מהאלקטרונים מעוררים תרמית לרמות מעל , אך בסך הכל יש שינוי קטן מ- . עם זאת, אם הפרש פוטנציאל מופעל על המתכת, אלקטרונים בעלי אנרגיות ליד אנרגיית פרמי דורשים רק כמות קטנה של אנרגיה נוספת מהשדה החשמלי המופעל כדי להגיע למצבי אנרגיה ריקים קרובים מעל אנרגיית פרמי. לכן, אלקטרונים במתכת החווים רק שדה חשמלי מופעל חלש חופשיים לנוע מכיוון שרמות ריקות רבות זמינות קרוב לרמות האנרגיה התפוסות. המודל של מתכות המבוסס על תיאוריית פסים מדגים שמתכות הן מוליכות חשמל מצוינות.

מבודדים

כעת נביט בשני פסי האנרגיה החיצוניים ביותר של חומר שבו הפס התחתון מלא באלקטרונים והפס העליון ריק ב- (איור 7.10). הפס התחתון המלא נקרא פס הערכיות, והפס העליון הריק הוא פס ההולכה. (פס ההולכה הוא זה שמלא חלקית במתכת.) נהוג להתייחס להפרדת האנרגיה בין פסי הערכיות וההולכה כרווח האנרגיה של החומר. אנרגיית פרמי נמצאת איפשהו ברווח האנרגיה כפי שמוצג באיור 7.10.

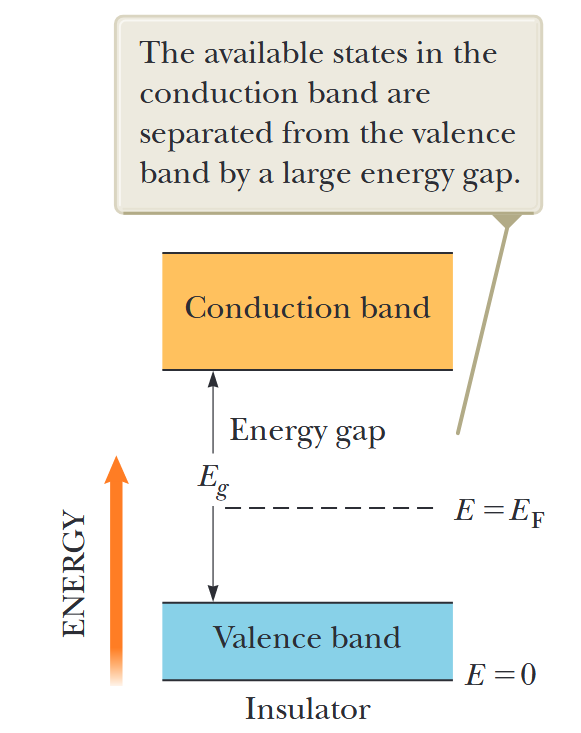
איור 7.11: למבודד חשמלי ב- יש פס ערכיות מלא ופס הולכה ריק. רמת פרמי נמצאת איפשהו בין הפסים הללו באזור הידוע כרווח האנרגיה. המצבים הזמינים בפס ההולכה מופרדים מפס הערכיות על ידי רווח אנרגיה גדול. (Serway et al., 2019).

נניח שלחומר יש רווח אנרגיה גדול יחסית של, לדוגמה, בערך . ב- (טמפרטורת החדר), , שהוא הרבה יותר קטן מרווח האנרגיה. בטמפרטורות כאלה, התפלגות פרמי-דיראק צופה שאלקטרונים מעטים מאוד מעוררים תרמית לפס ההולכה. אין מצבים זמינים הנמצאים קרוב באנרגיה מעל פס הערכיות ואליהם אלקטרונים יכולים לנוע כלפי מעלה כדי לטפל באנרגיה הקינטית הנוספת הקשורה לתנועה דרך החומר, בתגובה לשדה חשמלי. כתוצאה מכך, האלקטרונים אינם נעים; החומר הוא מבודד.

מוליכים למחצה

למוליכים למחצה יש את אותו סוג של מבנה פסים כמו מבודד, אך רווח האנרגיה קטן הרבה יותר, בסדר גודל של . טבלה מראה את רווחי האנרגיה עבור מספר חומרים שונים. מבנה הפסים של מוליך למחצה מוצג באיור 7.11. מכיוון שרמת פרמי ממוקמת ליד אמצע הרווח עבור מוליך למחצה, ו- קטן, מספרים נכבדים של אלקטרונים מעוררים תרמית מפס הערכיות לפס ההולכה.

ערכי רווח האנרגיה עבור כמה מוליכים למחצה:

גביש	() ב-	() ב-

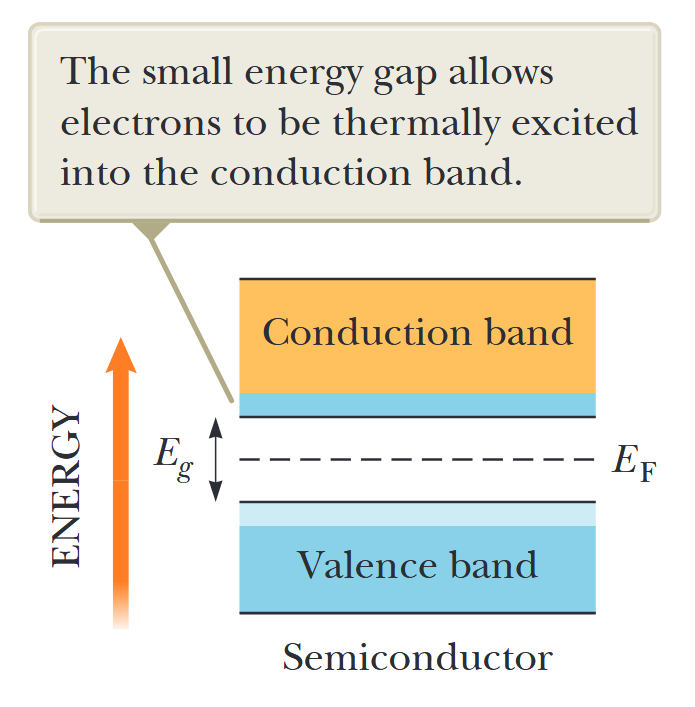
איור 7.12: מבנה פסים של מוליך למחצה בטמפרטורות רגילות (). רווח האנרגיה קטן בהרבה מאשר במבודד. רווח האנרגיה הקטן מאפשר לאלקטרונים להיות מעוררים תרמית לפס ההולכה. (Serway et al., 2019).

בגלל הרמות הריקות הרבות מעל הרמות המלאות תרמית בפס ההולכה, הפרש פוטנציאל קטן יכול בקלות להעלות את האלקטרונים בפס ההולכה למצבי אנרגיה זמינים, מה שגורם לזרם בינוני. ב-, כל האלקטרונים בחומרים אלה נמצאים בפס הערכיות ואין אנרגיה זמינה לעורר אותם על פני רווח האנרגיה. לכן, מוליכים למחצה הם מוליכים גרועים בטמפרטורות נמוכות מאוד.

מכיוון שהעירור התרמי של אלקטרונים על פני הרווח הצר סביר יותר בטמפרטורות גבוהות יותר, המוליכות של מוליכים למחצה עולה במהירות עם הטמפרטורה, בניגוד חד למוליכות של מתכות, שיורדת לאט עם עליית הטמפרטורה.

נושאי מטען במוליך למחצה יכולים להיות שליליים, חיוביים או שניהם. כאשר אלקטרון נע מפס הערכיות לפס ההולכה, הוא משאיר מאחוריו אתר פנוי, הנקרא חור, בפס הערכיות שאחרת היה מלא. החור הזה (אתר חסר אלקטרונים) פועל כנושא מטען במובן שאלקטרון חופשי מאתר קרוב יכול לעבור לחור. בכל פעם שאלקטרון עושה זאת, הוא יוצר חור חדש באתר שהוא נטש. לכן, ההשפעה הנטו יכולה להיראות כחור הנודד דרך החומר בכיוון הנגדי לכיוון תנועת האלקטרון. החור מתנהג כאילו הוא חלקיק עם מטען חיובי .

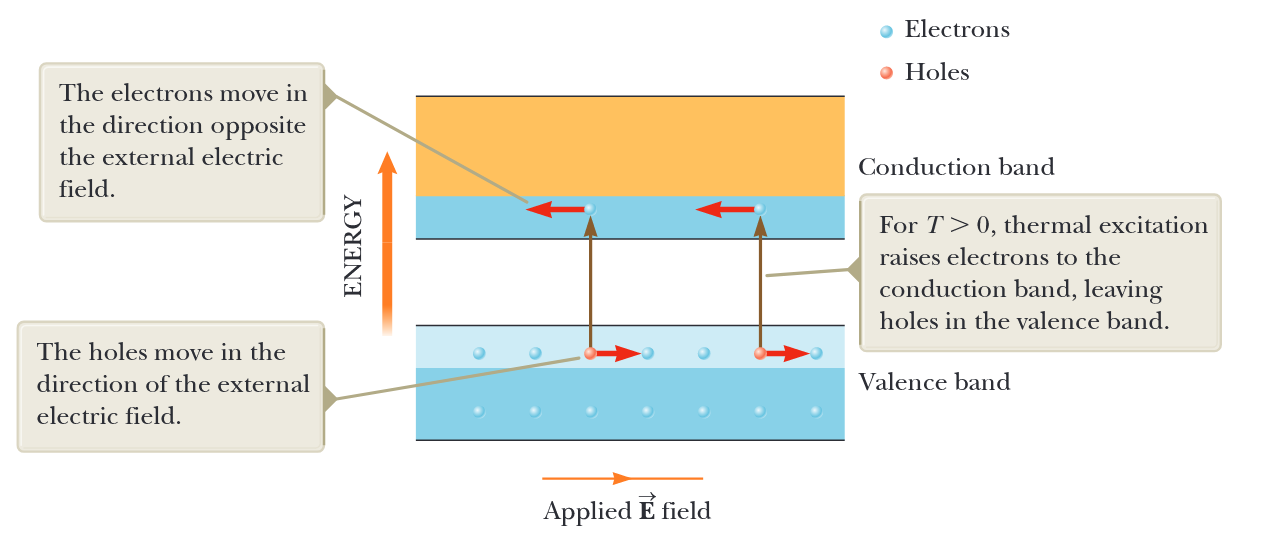
איור 7.13: תנועת מטענים (חורים ואלקטרונים) במוליך למחצה טהור. עבור , עירור תרמי מעלה אלקטרונים לפס ההולכה, ומשאיר חורים בפס הערכיות. האלקטרונים נעים בכיוון הנגדי לשדה החשמלי החיצוני. החורים נעים בכיוון השדה החשמלי החיצוני. (Serway et al., 2019).

גביש מוליך למחצה טהור המכיל רק יסוד אחד או תרכובת אחת נקרא מוליך למחצה טבעי. במוליכים למחצה אלה, יש מספרים שווים של אלקטרוני הולכה וחורים. שילובים כאלה של מטענים נקראים זוגות אלקטרון-חור. בנוכחות שדה חשמלי חיצוני, החורים נעים בכיוון השדה ואלקטרוני ההולכה נעים בכיוון הנגדי לשדה (איור 7.12). מכיוון שלאלקטרונים ולחורים יש סימנים נגדיים, שתי התנועות מתאימות לזרם באותו כיוון.

מוליכים למחצה מוסממים

כאשר זיהומים מתווספים למוליך למחצה, גם מבנה הפסים של המוליך למחצה וגם ההתנגדות שלו משתנים. התהליך של הוספת זיהומים, הנקרא סימום, חשוב בשליטה במוליכות של מוליכים למחצה. לדוגמה, כאשר אטום המכיל חמישה אלקטרונים בקליפה החיצונית, כמו ארסן, מתווסף למוליך למחצה מקבוצה IV, ארבעה מהאלקטרונים יוצרים קשרים קוולנטיים עם אטומי המוליך למחצה ואחד נשאר (איור 7.13 (a)). האלקטרון הנוסף הזה כמעט חופשי מהאטום האב שלו וניתן לעצב אותו כבעל רמת אנרגיה הנמצאת ברווח האנרגיה, מיד מתחת לפס ההולכה (איור 7.13 (b)).

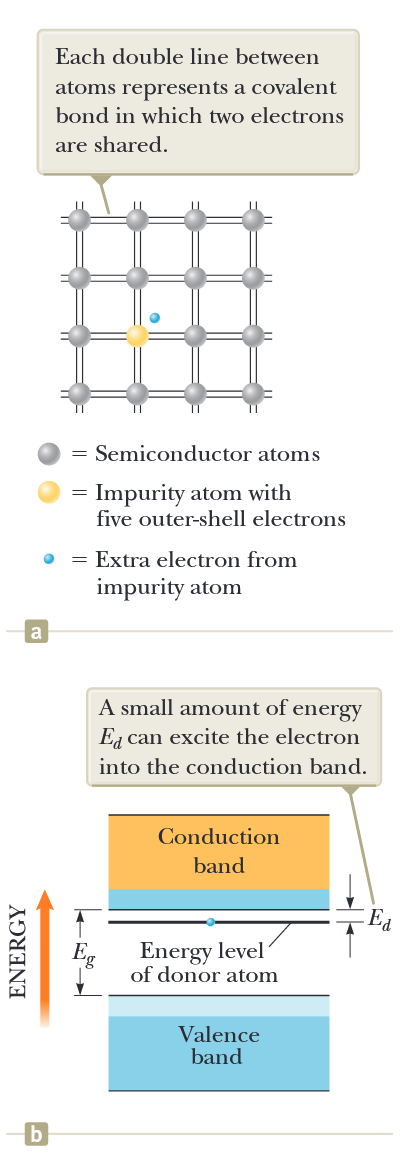
איור 7.14: מוליך למחצה מסוג n. (a) ייצוג דו-ממדי של מוליך למחצה המורכב מאטומי קבוצה IV (אפור) ואטום זיהום (צהוב) שיש לו חמישה אלקטרונים בקליפה החיצונית. כל קו כפול בין אטומים מייצג קשר קוולנטי שבו משותפים שני אלקטרונים. (b) דיאגרמת פסי אנרגיה עבור מוליך למחצה שבו האלקטרון הכמעט חופשי של אטום הזיהום נמצא ברווח האנרגיה, מיד מתחת לתחתית פס ההולכה. כמות קטנה של אנרגיה יכולה לעורר את האלקטרון לפס ההולכה. (Serway et al., 2019).

אטום חמש-ערכי כזה למעשה תורם אלקטרון למבנה ולכן מכונה אטום תורם. מכיוון שהמרווח בין רמת האנרגיה של האלקטרון של אטום התורם לתחתית פס ההולכה קטן מאוד (בדרך כלל, בערך ), נדרשת רק כמות קטנה של עירור תרמי כדי לגרום לאלקטרון זה לעבור לפס ההולכה. (זכרו שהאנרגיה הממוצעת של אלקטרון בטמפרטורת החדר היא בערך .) מוליכים למחצה מוסממים באטומי תורם נקראים מוליכים למחצה מסוג-n. לאלקטרוני התורם אין חור משויך, כך שרוב נושאי המטען בחומר הם אלקטרונים, שהם טעונים שלילית.

אם מוליך למחצה מקבוצה IV מסום באטומים המכילים שלושה אלקטרונים בקליפה החיצונית, כמו אינדיום ואלומיניום, שלושת האלקטרונים יוצרים קשרים קוולנטיים עם אטומי מוליך למחצה שכנים, כך שהם משאירים מחסור באלקטרונים - חור - במקום שבו הקשר הרביעי היה נמצא אם אלקטרון של אטום הזיהום היה זמין ליצור אותו (איור (a)). ניתן למדל מצב זה על ידי הצבת רמת אנרגיה ברווח האנרגיה, מיד מעל פס הערכיות, כמו באיור (b).

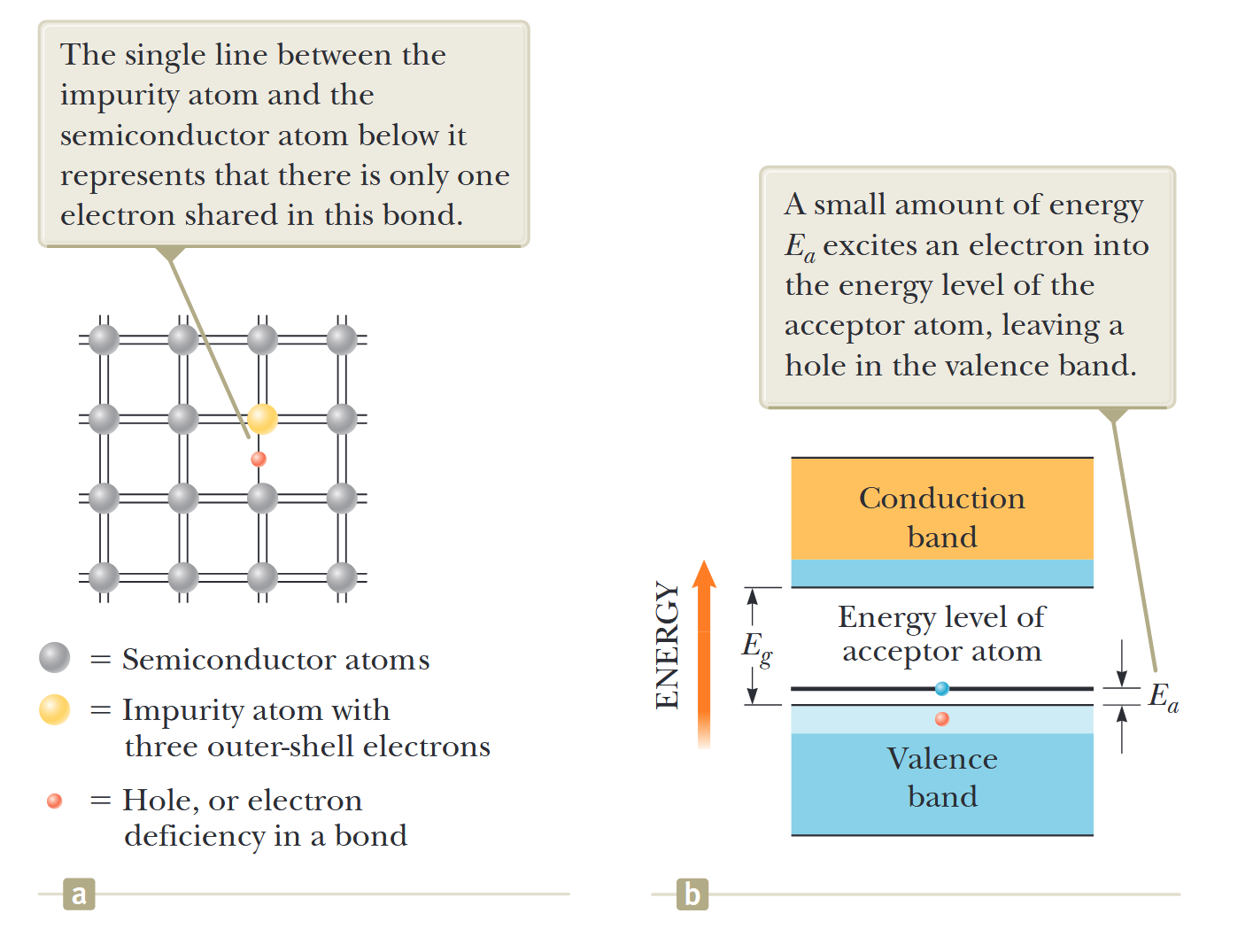
איור 7.15: מוליך למחצה מסוג p. (a) ייצוג דו-ממדי של מוליך למחצה המורכב מאטומי קבוצה IV (אפור) ואטום זיהום (צהוב) בעל שלושה אלקטרונים בקליפה החיצונית. הקו היחיד בין אטום הזיהום לאטום המוליך למחצה מתחתיו מייצג שיש רק אלקטרון אחד המשותף בקשר זה. (b) דיאגרמת פסי אנרגיה עבור מוליך למחצה שבו רמת האנרגיה המשויכת לאטום הזיהום התלת-ערכי נמצאת ברווח האנרגיה, מיד מעל לחלק העליון של פס הערכיות. כמות קטנה של אנרגיה מעוררת אלקטרון לרמת האנרגיה של אטום הקולט, משאירה חור בפס הערכיות. (Serway et al., 2019).

לאלקטרון מפס הערכיות יש מספיק אנרגיה בטמפרטורת החדר כדי למלא את רמת הזיהום הזו, ובכך הוא משאיר מאחוריו חור בפס הערכיות. החור הזה יכול לשאת זרם בנוכחות שדה חשמלי. מכיוון שאטום תלת-ערכי מקבל אלקטרון מפס הערכיות, זיהומים כאלה מכונים אטומי קולט. מוליך למחצה מוסמם בזיהומים תלת-ערכיים (קולט) ידוע כמוליך למחצה מסוג-p מכיוון שרוב נושאי המטען הם חורים טעונים חיובית.

כאשר הולכה במוליך למחצה היא תוצאה של זיהומי קולט או תורם, החומר נקרא מוליך למחצה חיצוני. הטווח הטיפוסי של צפיפויות סימום עבור מוליכים למחצה חיצוניים הוא עד , בעוד שצפיפות האלקטרונים במוליך למחצה טיפוסי היא בערך .

התקני מוליכים למחצה

האלקטרוניקה של המחצית הראשונה של המאה ה-20 התבססה על צינורות ריק, שבהם אלקטרונים עוברים דרך מרחב ריק בין קתודה לאנודה. ראינו התקני צינור ריק בדיונים קודמים על קרן אלקטרונים, מנגנון תומסון למדידת עבור האלקטרון, ומכשיר האפקט הפוטו-אלקטרי. הטרנזיסטור הומצא בשנת 1948, מה שהוביל למעבר מצינורות ריק לכיוון מוליכים למחצה כבסיס להתקנים אלקטרוניים. שלב זה של האלקטרוניקה נמשך כבר כמה עשורים. כפי שנדון בפרק קודם, ייתכן ושלב חדש של אלקטרוניקה יהיה בעתיד הקרוב באמצעות התקנים ננו-טכנולוגיים המשתמשים בנקודות קוונטיות ומבנים אחרים בקנה מידה ננומטרי. בחלק זה, אנו דנים בהתקנים אלקטרוניים המבוססים על מוליכים למחצה, שעדיין נמצאים בשימוש נרחב ויהיו כך עוד שנים רבות.

צומת דיודה

יחידה בסיסית של התקן מוליכים למחצה נוצרת כאשר מוליך למחצה מסוג-p מחובר למוליך למחצה מסוג-n ליצירת צומת p-n. צומת דיודה היא התקן המבוסס על צומת p-n יחיד. התפקיד של דיודה מכל סוג הוא להעביר זרם בכיוון אחד אך לא בשני. לכן, היא פועלת כשסתום חד-כיווני עבור זרם חשמלי.

הצומת p-n המוצגת באיור 7.14 מורכבת משלושה אזורים נפרדים: אזור p, אזור n, ואזור קטן הנמתח כמה מיקרומטרים לכל צד של הממשק, הנקרא אזור דלדול.

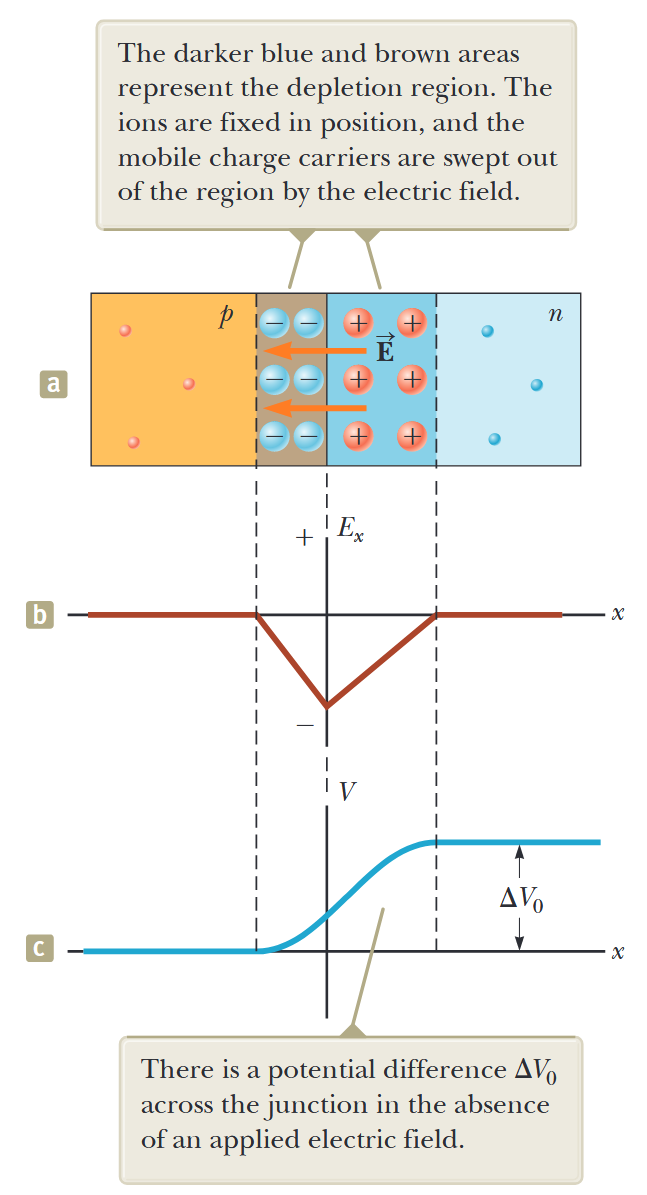
איור 7.16: צומת p-n. (a) סידור פיזיקלי של צומת p-n. האזורים הכחולים הכהים והחומים מייצגים את אזור הדלדול. היונים קבועים במקומם, ונושאי המטען הניידים נסחפים מהאזור על ידי השדה החשמלי. (b) רכיב של השדה החשמלי הפנימי מול עבור צומת p-n. (c) הפרש הפוטנציאל החשמלי הפנימי מול עבור צומת p-n. יש הפרש פוטנציאל על פני הצומת בהיעדר שדה חשמלי מופעל. (Serway et al., 2019).

ניתן לדמיין את אזור הדלדול כאזור הנוצר כאשר שני חצאי הצומת מובאים יחד. האלקטרונים התורמים הניידים בצד n הקרובים ביותר לצומת מתפזרים לצד p וממלאים חורים הממוקמים שם, ובכך משאירים מאחוריהם יונים חיוביים לא ניידים. בזמן שתהליך זה מתרחש, אנו יכולים למדל את החורים הממולאים כמתפזרים לצד n, כך שהם משאירים מאחוריהם אזור של יונים שליליים קבועים.

מכיוון ששני הצדדים של אזור הדלדול נושאים כל אחד מטען נטו, קיים שדה חשמלי פנימי בסדר גודל של עד באזור הדלדול. שדה זה מייצר כוח חשמלי על כל נושאי מטען ניידים נותרים הסוחף אותם מאזור הדלדול, הקרוי כך מכיוון שהוא אזור מדולדל מנושאי מטען ניידים. השדה החשמלי הפנימי הזה יוצר הפרש פוטנציאל פנימי המונע המשך דיפוזיה של חורים ואלקטרונים על פני הצומת ובכך מבטיח זרם אפס בצומת כאשר לא מופעל הפרש פוטנציאל.

פעולת הצומת כדיודה הכי קלה להבנה במונחים של גרף הפרש הפוטנציאל. אם מתח מופעל על הצומת כך שהצד p מחובר לקוטב החיובי של מקור מתח כמו שמוצג באיור 7.15 (a), הפרש הפוטנציאל הפנימי על פני הצומת יורד; הירידה גורמת לזרם שעולה אקספוננציאלית עם עליית המתח הקדמי, או הטיה קדמית. עבור הטיה הפוכה (כאשר צד n של הצומת מחובר לקוטב החיובי של מקור מתח), הפרש הפוטנציאל הפנימי עולה עם עליית ההטיה ההפוכה כמו באיור 7.15 (b); העלייה גורמת לזרם הפוך קטן מאוד שמגיע במהירות לערך רוויה .

איור 7.17: פעולת צומת דיודה. (a) צומת p-n תחת הטיה קדמית. התרשים העליון מראה את הפוטנציאלים המופעלים בקצוות הצומת. תחת זה יש תרשים מעגל המראה סוללה עם מתח מתכוונן. התרשים התחתון מראה כיצד הפוטנציאל משתנה על פני הצומת. (b) כאשר הסוללה הפוכה וצומת p-n תחת הטיה הפוכה, הזרם קטן מאוד. (c) העקומה האופיינית עבור צומת p-n אמיתית. תחת הטיה הפוכה, ההתנגדות גבוהה והזרם נמוך. תחת הטיה קדמית, ההתנגדות נמוכה והזרם גבוה. (Serway et al., 2019).

יחס הזרם-מתח עבור דיודה אידאלית הוא:

כאשר ה- הראשון הוא בסיס הלוגריתם הטבעי, ה- השני מייצג את גודל מטען האלקטרון, הוא קבוע בולצמן, ו- היא הטמפרטורה המוחלטת. איור 7.15 (c) מראה עלילת - אופיינית של צומת p-n אמיתית, המדגימה את התנהגות שסתום החד-כיווני.

דיודות פולטות אור וקולטות אור

דיודות פולטות אור (LEDs) ולייזרים מוליכים למחצה הם דוגמאות נפוצות של התקנים התלויים בהתנהגות מוליכים למחצה. LEDs משמשים בתצוגות טלוויזיה, תאורת בית, פנסים ויחידות פלאש למצלמה.

פליטה וקליטה של אור במוליכים למחצה דומה לפליטה וקליטה של אור על ידי אטומים גזיים, פרט שבדיון על מוליכים למחצה עלינו לשלב את הרעיון של פסי אנרגיה במקום רמות אנרגיה בדידות באטומים בודדים.

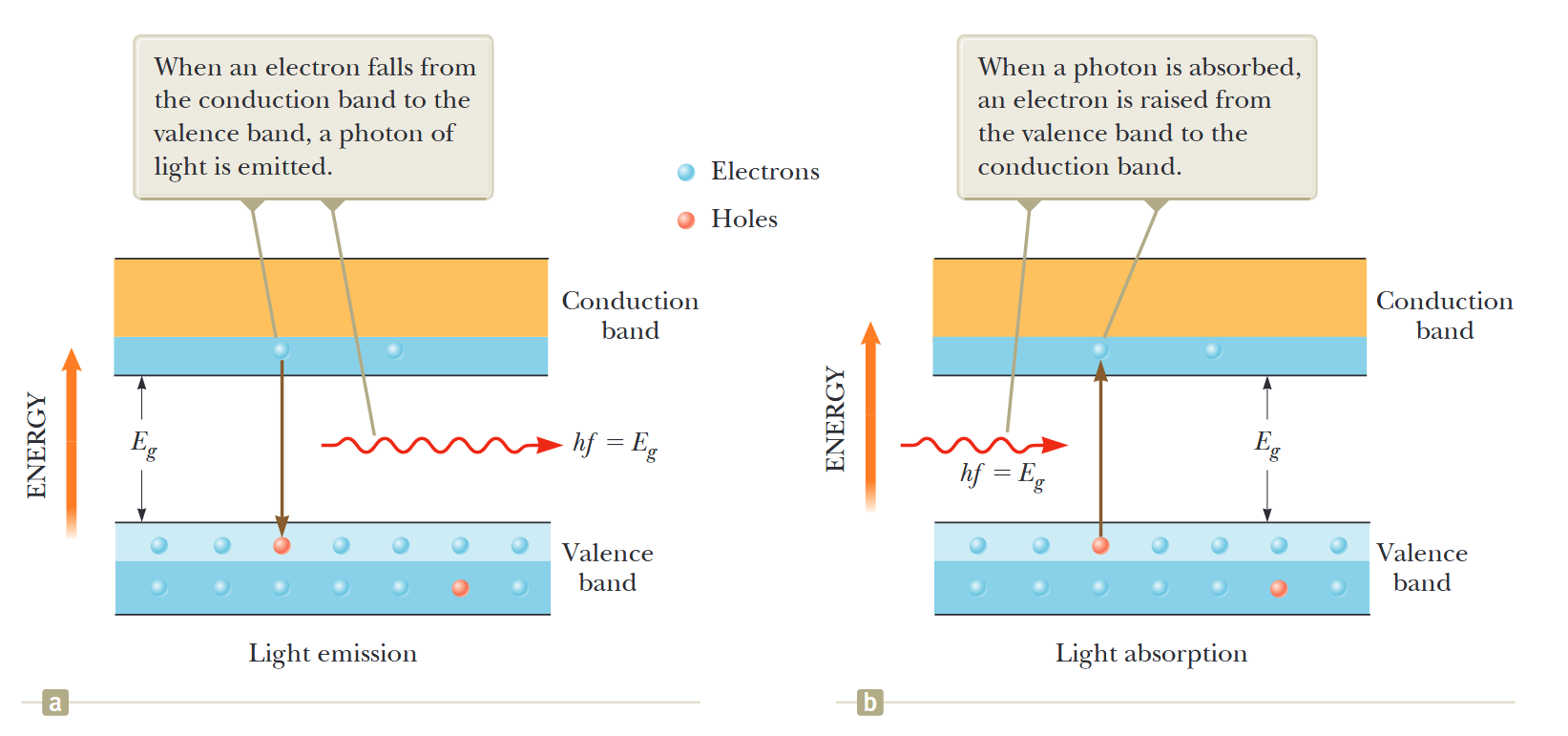
פליטה וקליטה של אור במוליכים למחצה. (a) פליטת אור ממוליך למחצה. כאשר אלקטרון נופל מפס ההולכה לפס הערכיות, נפלט פוטון אור. (b) קליטת אור על ידי מוליך למחצה. כאשר פוטון נקלט, אלקטרון מועלה מפס הערכיות לפס ההולכה. (Serway et al., 2019).

כפי שמוצג באיור 7.16 (a), אלקטרון המעורר חשמלית לפס ההולכה יכול להתאחד בקלות עם חור (במיוחד אם האלקטרון מוזרק לאזור p). כאשר איחוד זה מתרחש, נפלט פוטון באנרגיה . עם עיצוב נכון של המוליך למחצה והמעטפת הפלסטית או המראות הנלוות, האור ממספר גדול של מעברים אלה משמש כמקור LED או לייזר מוליכים למחצה.

להפך, אלקטרון בפס הערכיות עשוי לקלוט פוטון אור נכנס ולעלות לפס ההולכה, כך שהו משאיר חור מאחור (איור 7.16 (b)). האנרגיה הנקלטת הזו יכולה לשמש להפעלת מעגל חשמלי. התקן אחד הפועל על עיקרון זה הוא תא סולארי פוטו-וולטאי.

יישום מוקדם בקנה מידה גדול של מערכי תאים פוטו-וולטאיים הוא אספקת האנרגיה לחללית. במהלך השנים הראשונות של המאה הנוכחית, יישום של פוטו-וולטאיקה לייצור חשמל על הקרקע היה אחת הטכנולוגיות האנרגטיות הצומחות במהירות בעולם.

דוגמה: איפה השלט?

העריכו את רווח הפס של המוליך למחצה ב-LED האינפרה-אדום של שלט רחוק טיפוסי לטלוויזיה.

פתרון:

דמיינו אלקטרונים באיור 7.16 (a) שנופלים מפס ההולכה לפס הערכיות, כך שהם פולטים פוטונים אינפרה-אדומים בתהליך.

למדנו שאורך הגל של אור אינפרה-אדום נמצד בטווח של עד . בואו נבחר מספר שקל לעבוד איתו, כמו (שהוא לא הערכה רעה מכיוון ששלטים רחוקים פועלים בדרך כלל בטווח של עד ).

נעריך את האנרגיה של הפוטונים מהשלט הרחוק:

ערך זה מתאים לרווח אנרגיה של בערך במוליך למחצה של ה-LED.

הטרנזיסטור

המצאת הטרנזיסטור על ידי ג’ון בארדין (1908-1991), וולטר בראטיין (1902-1987) ווויליאם שוקלי (1910-1989) בשנת 1948 חוללה מהפכה מוחלטת בעולם האלקטרוניקה. על עבודה זו, שלושת האנשים האלה חלקו את פרס נובל בפיזיקה בשנת 1956. עד 1960, הטרנזיסטור החליף את צינור הריק ביישומים אלקטרוניים רבים. הופעת הטרנזיסטור יצרה תעשיית רב-טריליון דולר המייצרת התקנים פופולריים כמו מחשבים אישיים, מקלדות אלחוטיות, טלפונים חכמים, קוראי ספרים אלקטרוניים וטאבלטים.

צומת טרנזיסטור מורכב מחומר מוליך למחצה שבו אזור n צר מאוד כרוך בין שני אזורי p או אזור p כרוך בין שני אזורי n. בכל מקרה, הטרנזיסטור נוצר משני צמתי p-n. סוגי טרנזיסטורים אלה שימשו באופן נרחב בימים הראשונים של אלקטרוניקת מוליכים למחצה. במהלך שנות ה-60, תעשיית האלקטרוניקה המירה יישומים אלקטרוניים רבים מטרנזיסטור הצומת לטרנזיסטור אפקט שדה, שהרבה יותר קל לייצר ויעיל באותה מידה.

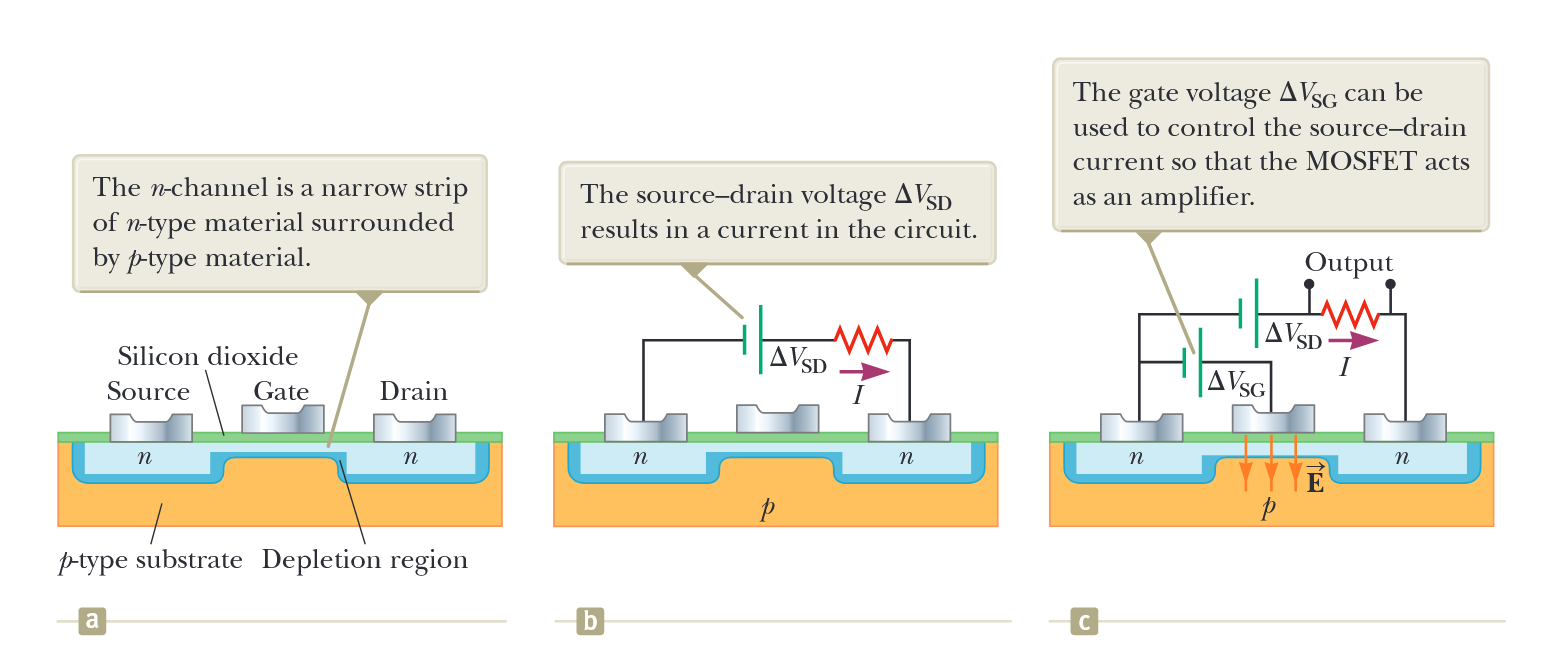
מבנה של טרנזיסטור אפקט שדה של מתכת-תחמוצת-מוליך למחצה (MOSFET). (a) המבנה של MOSFET. תעלת n היא רצועה צרה של חומר מסוג n המוקפת בחומר מסוג p. ב-(b): מתח מקור-ניקוז מופעל. מתח המקור-ניקוז גורם לזרם במעגל. (c) מתח שער מופעל. מתח השער יכול לשמש לשליטה בזרם מקור-ניקוז כך שה-MOSFET פועל כמגבר. (Serway et al., 2019).

איור 7.17 (a) מראה את המבנה של התקן נפוץ מאוד, ה-MOSFET, או טרנזיסטור אפקט שדה מתכת-תחמוצת-מוליך למחצה. סביר שאתם משתמשים במיליוני התקני MOSFET כאשר אתם עובדים על המחשב שלכם.

יש שלושה חיבורי מתכת (ה-M ב-MOSFET) לטרנזיסטור: המקור, הניקוז והשער. המקור והניקוז מחוברים לאזורי מוליך למחצה מסוג n (ה-S ב-MOSFET) בשני קצוות המבנה. אזורים אלה מחוברים על ידי תעלה צרה של חומר נוסף מסוג n, תעלת n. אזורי המקור והניקוז ותעלת n מוטמעים בחומר מצע מסוג p, היוצר אזור דלדול, כמו בצומת דיודה, לאורך החלק התחתון של תעלת n. השער מופרד מתעלת n על ידי שכבה של סיליקון דו-חמצני מבודד (ה-O ב-MOSFET, עבור תחמוצת). לכן, הוא אינו יוצר מגע חשמלי עם שאר החומר המוליך למחצה.

דמיינו שמקור מתח מופעל על פני המקור והניקוז כמו שמוצג באיור 7.17 (b). במצב זה, אלקטרונים זורמים דרך האזור העליון של תעלת n. אלקטרונים אינם יכולים לזרום דרך אזור הדלדול בחלק התחתון של תעלת n מכיוון שאזור זה מדולדל מנושאי מטען.

כעת מתח שני מופעל על פני המקור והשער כמו באיור 7.17 (c). הפוטנציאל החיובי על אלקטרודת השער גורם לשדה חשמלי מתחת לשער המכוון כלפי מטה בתעלת n (השדה ב”אפקט שדה”). שדה חשמלי זה מפעיל כוחות כלפי מעלה על אלקטרונים באזור מתחת לשער, גורם להם לנוע לתעלת n. כתוצאה מכך, אזור הדלדול הופך קטן יותר, מרחיב את האזור שדרכו יש זרם בין החלק העליון של תעלת n לאזור הדלדול. ככל שהאזור מתרחב, הזרם עולה.

אם מתח משתנה, כמו זה הנוצר ממוזיקה המאוחסנת בזיכרון של טלפון חכם, מופעל על השער, האזור שדרכו קיים זרם מקור-ניקוז משתנה בגודל לפי מתח השער המשתנה. שינוי קטן במתח השער גורם לשינוי גדול בזרם ומתח גדול מתאים על פני הנגד באיור 7.17 (c). לכן, ה-MOSFET פועל כמגבר מתח. מעגל המורכב משרשרת טרנזיסטורים כאלה יכול לגרום לאות ראשוני קטן מאוד ממיקרופון להיות מוגבר מספיק כדי להניע רמקולים חזקים בקונצרט חוצות.

הערות שוליים

1. הפונקציות נקראות פולינומי לגר (Laguerre polynomials). ניתן למצוא אותן בטיפול הקוונטי של אטום המימן בספרי לימוד מודרניים בפיזיקה. ↩

→ קודם: PHY3_006הבא: PHY3_008 ←