DVI1_HW002 פרויקטון 2

	סטודנט א’	סטודנט ב’
שם	עידו פנג בנטוב	יובל הנדל
ת”ז	CLASSIFIED	CLASSIFIED
דואר אלקטרוני	CLASSIFIED	CLASSIFIED

הקוד נמצא בGitHub.

---

---

הערה:

ציון:

חלק א’

שאלה 1

שרטוט המערכת.

ניתן להגדיר את כלל המערכת בעזרת קואורדינטה מוכללת אחת . נמצא את הלגראנז’יאן:

כאשר הוא אורך הקפיץ הימני (וגם השמאלי, כי המערכת סימטרית). נשים לב ש- , ולכן:

לכן ממשוואות לגראנז’, כאשר נשים לב שהכוח המוכלל כתוצאה מהריסון הוא :

נסמן את הכוח המופעל ע”י הקפיצים ע”י:

---

---

נסמן את האיבר הלא לינארי של הכוח ב-:

כאשר:

נפתח את לטיילור לפי , סביב :

נציב בחזרה בכוח הקפיצים:

לפי ההנחיות, נזניח את הפרמטרים ממעלה שלישית ומעלה. נישאר עם:

נציב בחזרה במשוואת התנועה (1.1):

שאלה 2

עם נרמול הזמן , נשים לב כי וגם נציב במשוואה (1.2) ונחלק במסה וב-:

נציב את שאר הנרמולים:

ננרמל את ל- (בעזרת חילוק ב-):

כאשר:

עם (ביחידות של ).

שאלה 3

נבצע טרנספורמציה של הקואורדינטות לפי . נשים לב:

נציב ב-(2.1):

נסדר:

נסמן :

כאשר נשים לב ש- . נסמן:

ולכן:

קיבלנו בדיוק את אותן המשוואות מהתרגול.

---

---

• עבור , המערכת היא: כאשר הסימון הוא עבור המקרה הספציפי של .
  הפתרון של מערכת כזאת הוא פתרון ידוע: כאשר: כאשר .
• עבור , המערכת היא: כאשר הסימון הוא עבור המקרה הספציפי של .
  הפתרון: כאשר: כאשר .

ראשית, נפרוש את מרחב הפתרונות בעזרת מתן שני תנאי התחלה בת”ל:

כעת נתפור את הפתרון עבור כל זמן . נדרוש שהמיקום והמהירות בכל זמן יהיו רציפים ולכן עלינו לדרוש:

נקבל את מערכת המשוואות:

נציב את ואת כדי לקבל (עבור ):

ניתן לכתוב בצורה מטריצית:

נפתור עבור ו-:

באותו אופן עבור נקבל:

הפתרון שמתקבל יהיה סופרפוזיציה של ו- בחצי המחזור הראשון, ו- בחצי המחזור השני.

בהרצאה, ראינו שעבור , הפתרונות מקיימים:

אם נביא זאת למונחים של , מאחר והגדרנו , זה הופך ל:

נרצה לדעת עבור איזה אנו מקבלים מעבר בין תחום יציב ללא יציב. באותו אופן כמו בהרצאה, נקבל תנאי (אחר מההרצאה) לגבולות האי יציבות:

או פשוט:

ניתן להראות מהפולינום האופייני של הבעיה שהערכים העצמיים מקיימים:

כאשר:

ו- ללא סימון אינדקס הוא ה- בהגדרת (ה- של הריסון, לא של הע”ע).
לכן, כדי למצוא את גבולות האי יציבות, עלינו למצוא את העקומות המקיימות:

נציב את הגדרת :

מהצבת הפתרונות שקיבלנו נקבל:

לאחר ההצבה נקבל ביטוי לשני עקומים:

נשים לב ש:

בנוסף, כיוון ש- :

קיבלנו שני עקומים במונחים של המייצגים את קווי הגבול של אזורי האי-יציבות הפרמטרית של המערכת.

---

---

שאלה 4

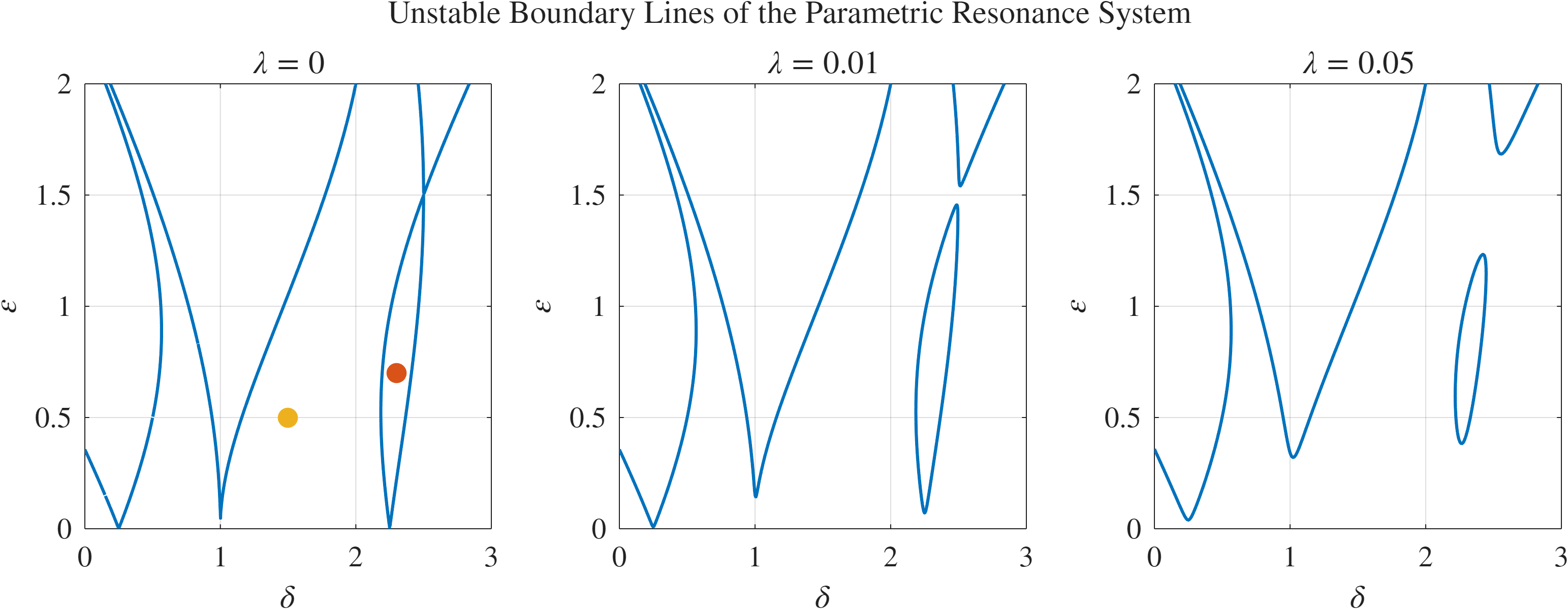
איור 1: דיאגרמת Strutt של הבעיה הנתונה.

נשים לב שעבור ריסון אפסי, , קיבלנו דיאגרמה זהה לזו שקיבלנו בתרגול.

שאלה 5

נחזור ל-(2.1):

ונזכור גם את (2.2):

עם .
נקבל:

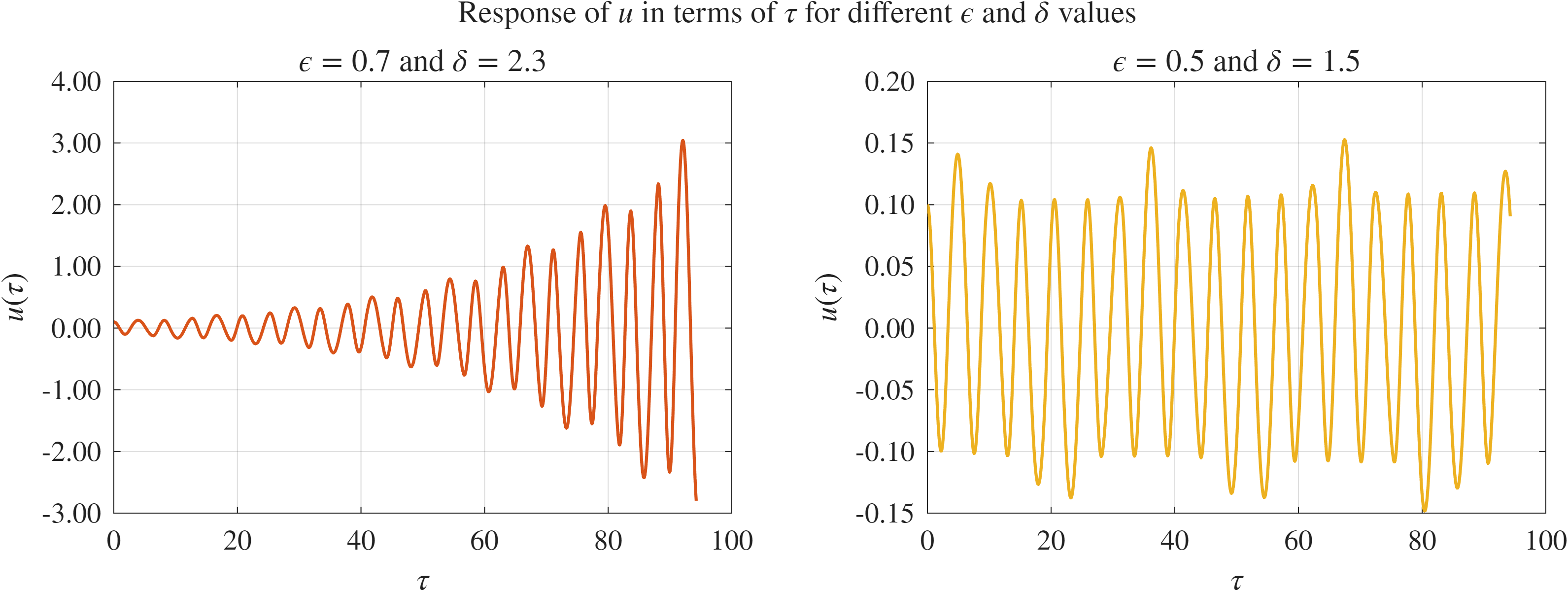
איור 2: תגובה נומרית מחוץ ובתוך הלשוניות.

---

---

חלק ב’

איור 3: סכמת הבעיה.

שאלה 1

ניתן לתאר את דינמיקת המערכת עם , ולכן מספר דרגות החופש הוא :

שאלה 2

קצת גאומטרייה:

איור 4: גאומטריית המטוטלות.

נשים לב כי:

לכן נקבל שהגודל הוא (לאחר זהויות טריגונומטריות):

המיקומים של מסה:

האנרגיה הקינטית היא סכום האנרגיה הקינטית של כל חלקיק בר מסה במערכת:

מבחינת אנרגיה פוטנציאלית, יש לנו את אנרגיית הקפיץ והאנרגיה הפוטנציאלית הכבידתית (עם נקודת ייחוס בראשית):

נתון גם כי פונקציית ריילי של המערכת:

שאלה 3

הלגראנז’יאן במקרה שלנו, מתוך משוואות (2.2) ו-(2.3):

נשים לב כי:

כדי לחשב את נצטרך למצוא קודם את :

כעת נוכל לחשב את ו-:

נתייחס לכוחות המוכללים:

מאחר ונתונה לנו פונקציית דיסיפציה של ריילי, יופיע לנו גם בצד הימני של משוואות התנועה:

נציב במשוואות לגראנז’:

אם נציב גם את :

שאלה 4

נבצע את הנרמול על משוואת התנועה עבור . נחלק את (3.2) ב-:

ננרמל גם את הזמן לפי , כך שהנגזרות של :

נציב גם את הנרמולים האחרים ונישאר עם:

עבור הקואורדינטה השנייה, :

שאלה 5

במקרה שבו אין ריסון, משוואות התנועה שלנו הן:

ניתן להבין מהאיור שאחת מנקודות שיווי המשקל היציבות היא:

---

---

נבצע לינאריזציה סביבה, כאשר נשים לב שבמקרה המיוחד הנ”ל, , ולכן:

נגזור את לפי , ונציב את , ונישאר עם המטריצה הפשוטה הבאה:

לכן משוואות התנועה לאחר לינאריזציה:

נוח לנו לעבוד עם הצורה הבאה למערכות בשתי דרגות חופש:

לכן, במקרה שלנו:

שאלה 6

על מנת למצוא תדרים עצמיים נפתור בעיית ערכים עצמיים מוכללת של הצמד ו-:

ונדרוש פתרון לא טריוויאלי.
נקבל ב-MATLAB שהתדרים העצמיים:

וקטורים מודליים (לא מנורמלים):

נסמן:

כך שנוכל לרשום:

שאלה 7

ניעזר בתכונות האורתוגונליות של המודים:

נמצא כי:

וקטור מודלי הוא עד כדי כפל בקבוע, ויהיה לנו נוח לעבור עם מודים מנורמלים:

כאשר נבחר כך ש:

מה שאומר ש:

כלומר, כל מוד מחלקים ב- כך שמקבלים מוד מנורמל מסה. כעת נוכל להרכיב את המטריצה המודלית הטבעית:

---

---

שאלה 8

נשים לב ש:

וגם:

כעת, בעזרת המטריצה המודלית אנו יכולים לבצע מעבר בסיס למשוואות התנועה כדי לקבל משוואות תנועה שהן לא מצומדות. אנו עושים זאת בעזרת קואורדינטות מודליות טבעיות שמוגדרות ע”י:

כלומר, אנו מתארים את הקואורדינטות המוכללות כקומבינציה לינארית של עמודות . כלומר, מתארים את זוויות המערכת כקומבינציה לינארית של המודים. נציב את מערכת הקואורדינטות במשוואות התנועה:

נכפיל ב- משמאל:

נישאר עם:

קיבלנו 2 משוואות לא מצומדות. אם אין כוחות חיצוניים:

הערה של הבודק:

יש תוצאות אבל חסרים הסברים.

שאלה 9

נניח כעת ש:

כאשר נציב בחזרה בתדירויות הטבעיות נקבל את הביטויים הפשוטים הבאים:

וגם:

כך שלפי (7.1):

נשים לב גם ש:

בהינתן תנאי התחלה ללא מהירות:

נמיר לתנאי התחלה במובנים של הקואורדינטות המודליות :

נזכור ש- , ולכן ולכן נוכל לרשום את תנאי התחלה בצורה הבאה:

נחזור למשוואות התנועה הלא מצומדות שקיבלנו בשאלה קודמת:

נזכור שעבור עירור חופשי תגובת המערכת הרמונית, ולכן נוכל להניח פתרון מהצורה:

נמיר בחזרה לקואורדינטות פיזיקליות:

כמשוואות:

נציב את ו-:

מצאנו כבר את :

נציב את :

נסמן:

כדי שיתקיים משטר פעימות, נרצה לראות מתי יתקיים:

כך שבמוד הטבעי הראשון שתי המטוטלות נעות כמטוטלת אחת. לעומת זאת, עבור המוד השני, המטוטלות נמצאות בהפרש פאזה של .
נציב:

נמיר בחזרה לפרמטרי המערכת. נשים לב ש:

לכן, עם התנאים שרשמנו:

או פשוט:

כלומר, גם המסות וגם מרחקי הקפיץ מציר המטוטלות צריכים להיות זהים בכל מטוטלת.

שאלה 10

כפי שראינו בשאלה קודמת:

נוכל שרירותית לבחור (כי זה וקטורים עצמיים), כך שבעזרת התנאי לפעימות (9.1), נקבל:

אם ניקח למשל את תנאי ההתחלה:

ונציב ב-(0.1):

בעזרת זהויות טריגונומטריות נקבל:

נסמן:

כאשר היא למעשה תדירות הפעימות ו- היא התדירות הממוצעת (התדירות המהירה).
בהנחה ואמפליטודת המעטפת של שתי המטוטלות משתנה באופן איטי ביחס לתנודות המהירות של המטוטלות, נוכל לרשום:

עם הנחה זאת, יתקיים:

לכן, במקרה הספציפי הזה, עם תנאי ההתחלה האלו, וקבוע קפיץ חלש זה, נוכל להתייחס לפונקציות ו- כפונקציות הרמוניות עם תדירות ואמפליטודות המשתנות באופן איטי לפי ו- , בהתאמה.

שאלה 11

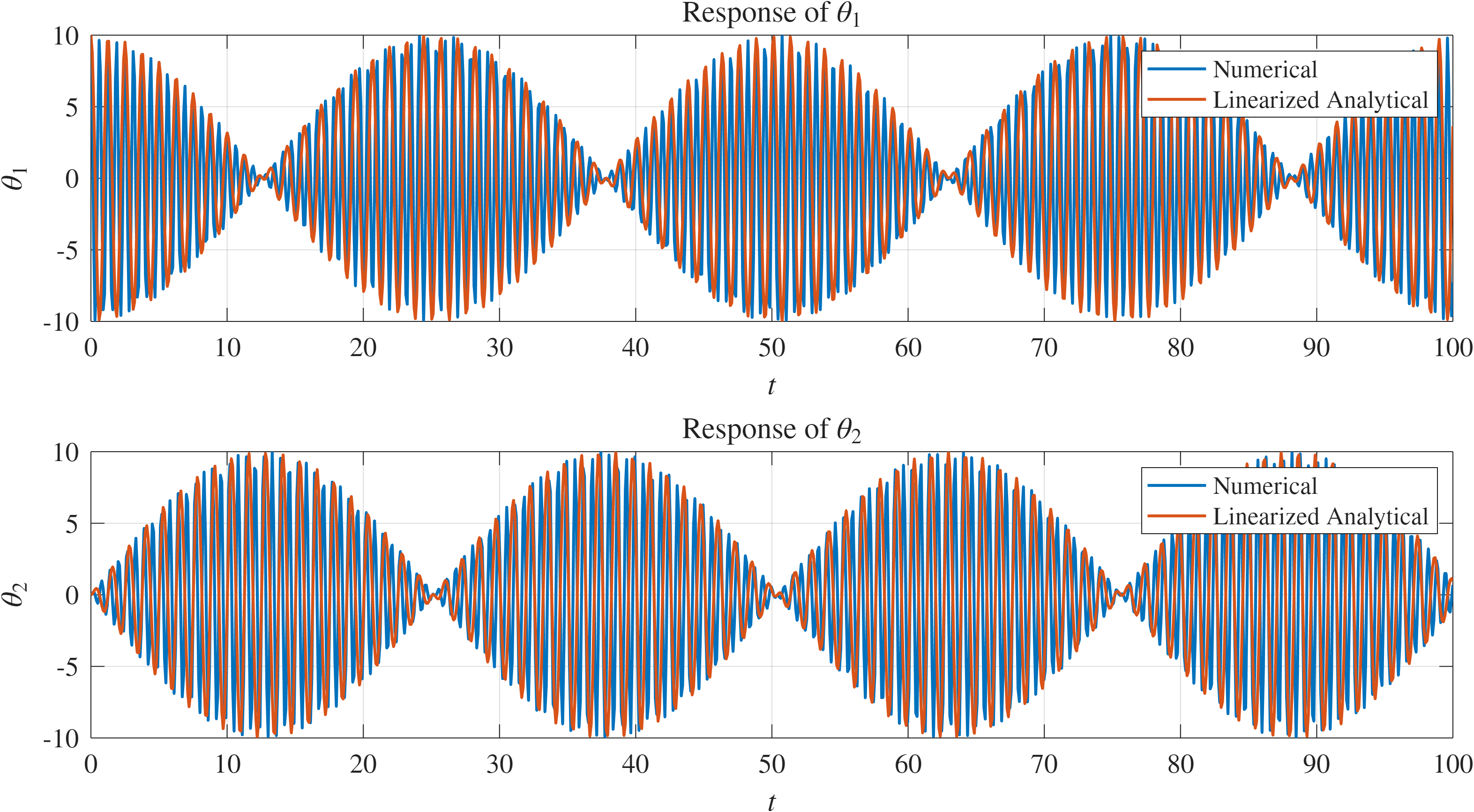
איור 5: תגובת המערכת בחישוב נומרי ואנליטי לאחר לינאריזציה.

שאלה 12

משוואות התנועה בקואורדינטות מודליות הן:

כאשר הוא וקטור העומסים, ו- היא מטריצת הריסון מודלית שנמצא אותה בהמשך. שאר הגדלים זהים לגדלים שקיבלנו בשאלה 8.
עבור תנאי התחלה כללי, אנו יודעים שבמצב מתמיד הפתרון הוא מהצורה:

---

---

נציב במשוואות התנועה המודליות ונקבל (לאחר חילוק ב-):

כאשר הוא:

נעביר אגף:

נעבור לקואורדינטות פיזיקליות. כיוון ש- , אז:

היפוך של מטריצה אלכסונית הוא פשוט לחלק באיברי האלכסון. יותר נוח להציג את חישוב זה כמה שנקרא סכום מודלי:

עלינו רק למצוא מהם ו-.

נשים לב שבמערכת המקורית (שאלה 4), מאחר וכעת יש ריסון, מטריצת הריסון היא:

נניח כי , אחרת לא נוכל לקבל ריסון מודלי, ואנו לא יודעים לפתור את הבעיה. לכן:

נוכל ממנה לחשב את מטריצת הריסון המודלית פשוט ע”י טרנספורמציה לפי :

מאחר והצורה הסטנדרטית של היא:

נסיק כי:

מצאנו את כל הביטויים עבור (2.1), ולכן אנו יודעים לנסח את תגובת המערכת במצב מתמיד:

שאלה 13

נשים לב שעם התנאים הנתונים, אנו מקבלים את אותם הערכים משאלה 9, רק הפעם נוכל כבר להציב ערכים כדי לפשט את הבעיה. בנוסף, נניח ש- ונמצא את התדרים המתאימים:

ואז המטריצה המודלית:

נניח כי הריסון הנתון הוא ריסון מודלי, כך ש:

לכן, לפי (2.2) ו-(2.1), התגובה במצב מתמיד (רק האמפליטודה) היא:

נוכל כעת לפתח את תגובת התדירות באופן גרפי:

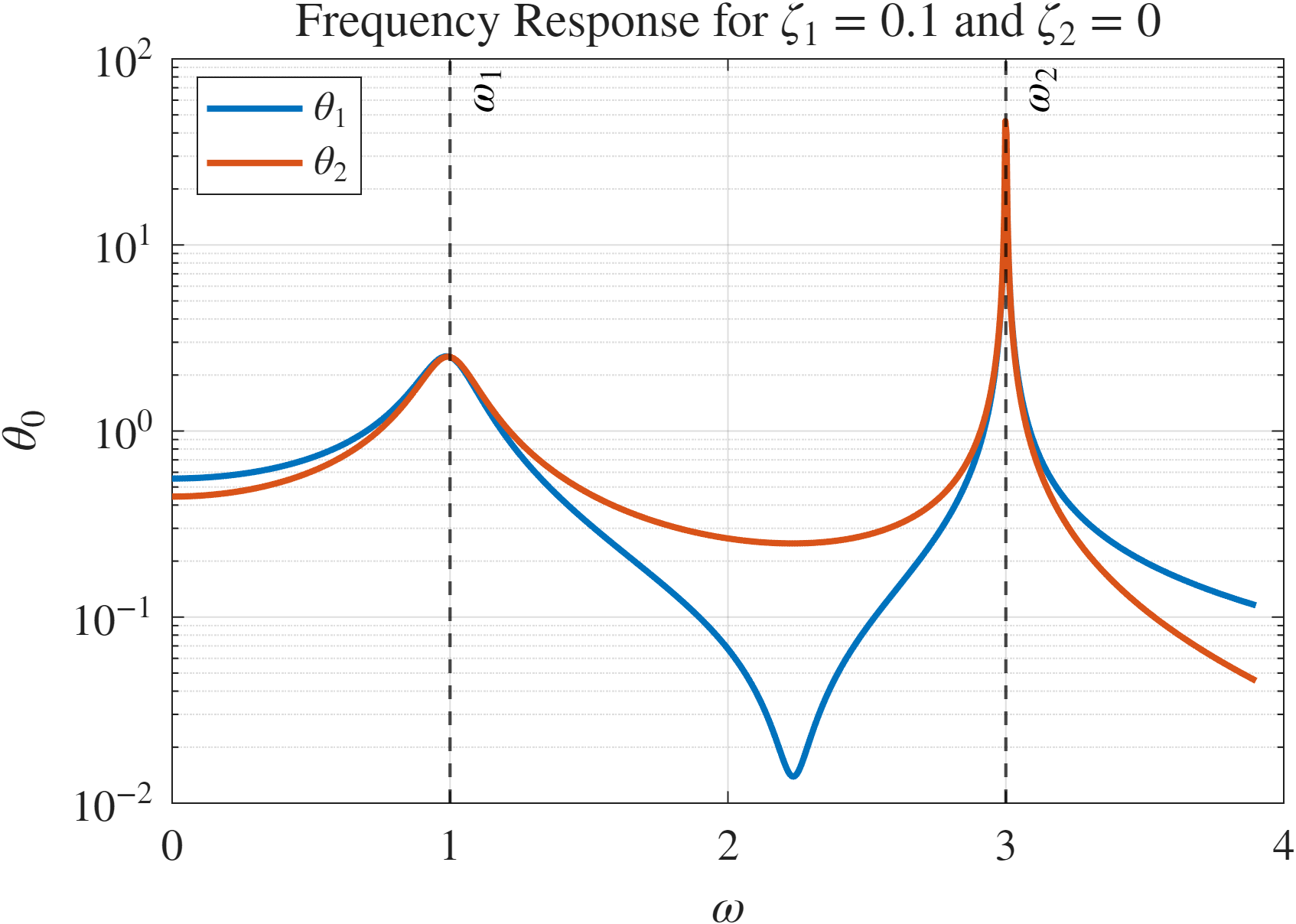
איור 6: תגובת התדירות של המערכת הנתונה.

ניתן לראות שאנו מקבלים אנטי-רזוננס עבור בתדירות בין ו-, בעוד הרזוננס בתדירות הטבעית השנייה, , לא מושפע כלל כתוצאה מהריסון, מאחר ו- .

נתמקד כעת רק ב-, ונריץ עבור ערכי שונים:

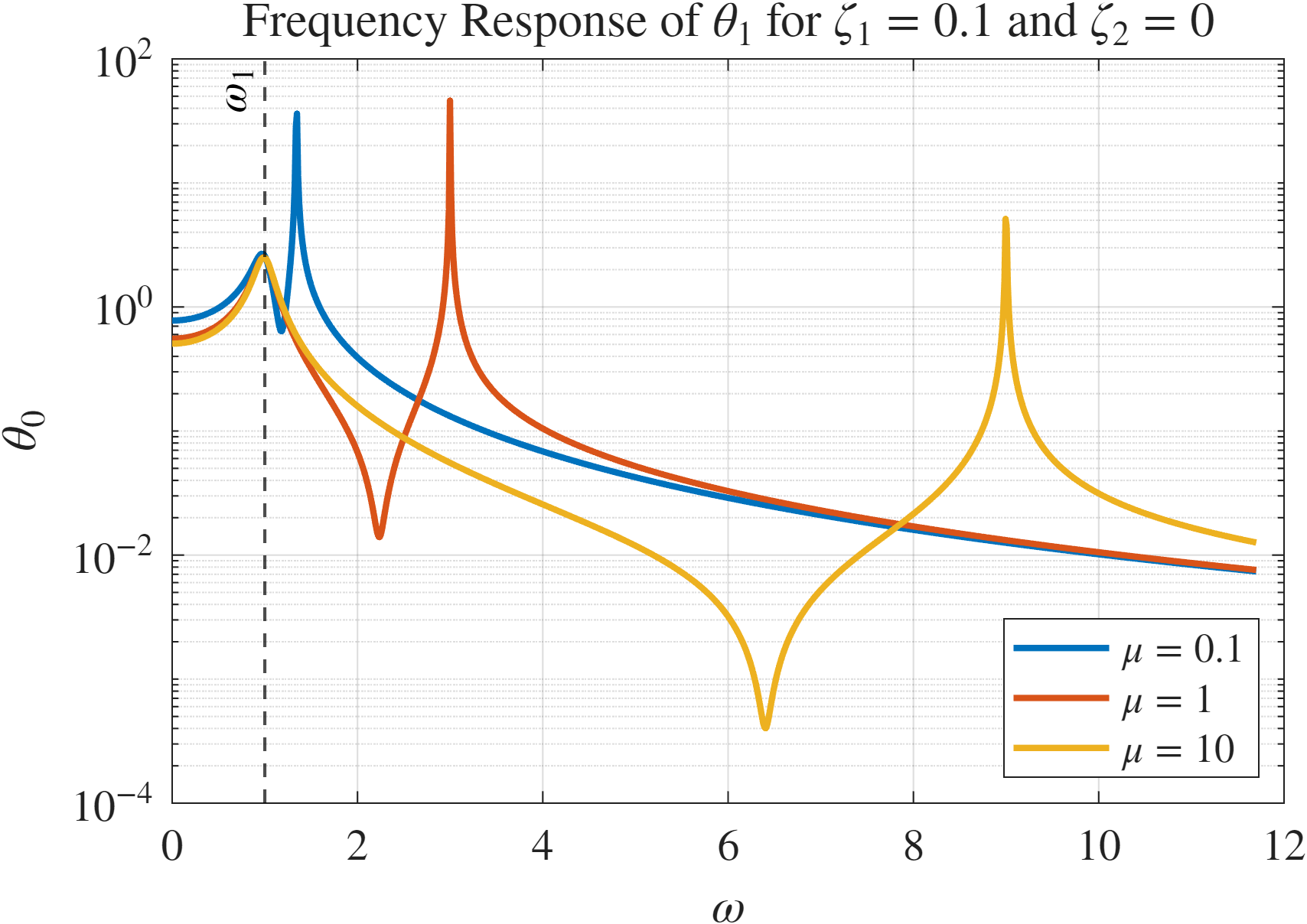
איור 7: תגובת התדירות של עבור ערכי שונים. זהה בכולם, בעוד תלוי ב-.

נשים לב שבתדירות המוד הראשון, , לא משנה מהו , ההגבר יישאר זהה.

הערה של הבודק:

חסר הסבר על המודים שהתקבלו.