ELM1_001 מעגלים מגנטיים בזרם ישר

מבוא

חפירה חפירה חפירה…
צריך להיזכר מחדש מה לעזאזל עשינו בפיזיקה 2, כמו למשל:

• מגנטיות
• חוק אמפר
• משוואות מקסוול
• השראות עצמית

מעגלים מגנטיים

ממשוואות מקסוול ניתן לראות דמיון רב בין חשמל ומגנטיות. ולכן, כמו שיש מעגלים חשמליים, ישנם גם מעגלים מגנטיים. להלן דוגמה למעגל מגנטי פשוט:

מעגל מגנטי פשוט.

ראשית, הוא כולל ליבה מגנטית. הליבה יכולה להיות עשויה מחומר אחד כמו פלדה, אבל גם יכולה לכלול מספר חלקים - גם המרווח אוויר נחשב. מסביב לליבה יש לפחות ליפוף אחד של חוט מוליך. כפי שאנו מכירים מפיזיקה, כאשר נזרים זרם דרך הסליל, ייווצר שטף מגנטי, , בליבה. מאחר ושטף זה מוגבל בשטח החתך של הליבה, , אנו יכולים למצוא את צפיפות השטף המגנטי, :

חוק הופקינסון

ניזכר בחוק אוהם:

במעגלים מגנטיים, יש חוק מקביל הנקרא חוק הופקינסון (שניתן לפתחו מחוק אמפר):

משפט:

חוק הופקינסון קובע כי:

כאשר:

• הוא הכוח המגנטומניע (כמ”מ) - magnetmotive force (MMF).
• הוא השטף המגנטי, כאשר .
• הוא הרילקטנס (reluctance) - ההתנגדות לשטף המגנטי, כאשר

הכוח המגנטומניע מקביל למקור מתח, השטף המגנטי הוא כמו הזרם החשמלי, והרילקטנס מתנהג כמו ההתנגדות. בנוסף, הכוח המגנטומניע הוא מכפלה של הזרם העובר דרך סליל ומספר הכריכות בו:

כאשר הוא מספר הכריכות ו- הוא הזרם.

ניזכר שמהגדרת ההתנגדות החשמלית:

כאשר הוא השטף החשמלי, הוא אורך הנגד ו- הוא שטח החתך של הנגד.
לרילקטנס יש הגדרה דומה:

הגדרה:

ההתנגדות לשטף מגנטי, הרילקטנס מוגדר עבור חומר עם תכונות אחידות באופן הבא:

כאשר:

• הוא אורך החומר
• הוא שטח החתך של החומר
• הוא הפרמיביליות של החומר, כאשר

שדה מגנטי וצפיפות שטף מגנטי

כאשר שטף מגנטי קיים בגוף כלשהו, הוא נוצר כתוצאה משדה מגנטי , הנתון ע”י:

כאשר:

• הוא עוצמת השדה המגנטי,, כאשר .
• כוח אלקטרומגנטי הפועל על הגוף, כאשר (לפעמים גם אומרים ).
• אורך הגוף.

עקומות B-H

עקומת B-H של ריק

בריק, צפיפות השטף המגנטי פרופורציונית לעוצמת השדה המגנטי ע”י המשוואה

כאשר

• הוא צפיפות השטף המגנטי, .
• היא עוצמת השטף המגנטי.
• קבוע הפרמביליות המגנטית של ריק ().

עקומת ה- של ריק קו ישר. הריק אף פעם לא מגיע למצב רוויה, לא משנה כמה גדולה צפיפות השטף המגנטי.

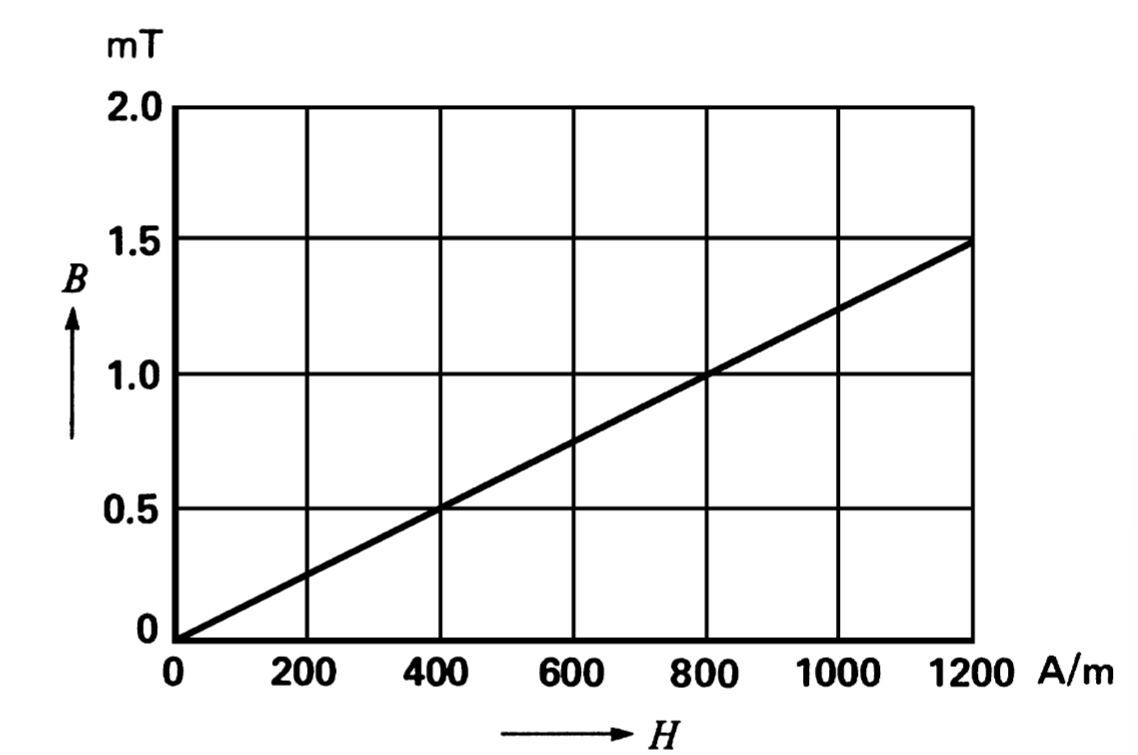
עקומת של ריק וחומרים לא-מגנטיים. (Wildi, 2014).

לחומרים לא-מגנטיים כמו נחושת, נייר, גומי ואוויר יש עקומות כמעט זהים לעקומה של ריק.

עקומת B-H של חומר מגנטי

צפיפות השטף המגנטי בחומר מגנטי גם תלויה בעוצמת השדה המגנטי אליו היא נתונה. ערכו הוא:

כאשר כאן הוא הפרמביליות היחסית של החומר. הערך שלו לא קבוע, ולמעשה משתנה כתלות בצפיפות השטף המגנטי בחומר. לכן, הקשר בין ו- הוא לא לינארי, ולכן לפעמים נעדיף להראות את הקשר ע”י העקומת .

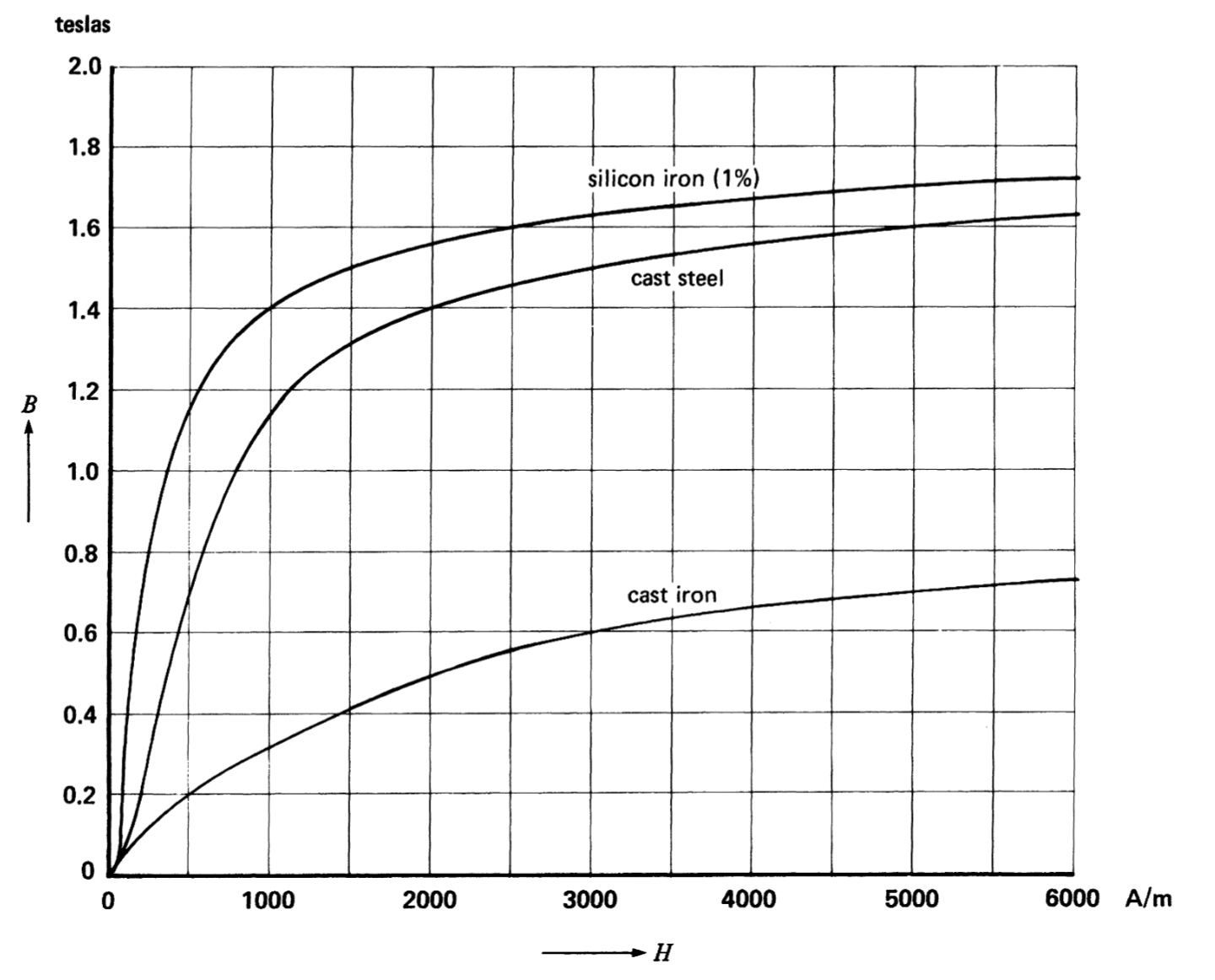
עקומות של שלושה חומרים מגנטיים. (Wildi, 2014).

אנלוגיה חשמלית

סיכום האנלוגיות:

חשמלי	יחידות	מגנטי	יחידות
כוח אלקטרומניע (כא”מ) -		כוח מגנטומניע (כמ”מ) -
התנגדות חשמלית -		רילקטנס מגנטי -
שטף חשמלי -		שטף מגנטי -
שדה חשמלי -		שדה מגנטי -
צפיפות זרם חשמלי -		צפיפות שטף מגנטי -
התנגדות סגולית -		השראות -
מוליכות חשמלית סגולית -		פרמביליות מגנטית סגולית -

הערה:

נזכור כי הפרמביליות של הריק היא . נניח בקורס שהפרמביליות של האוויר בקירוב זהה לגודל זה - .

מגנטיות

כיוון הכוח הפועל על מוליך ישר

כאשר מוליך נושא זרם, הוא מוקף בשדה מגנטי. עבור זרם אל תוך המסך, לקווים ההיקפיים יש הכיוון הבא:

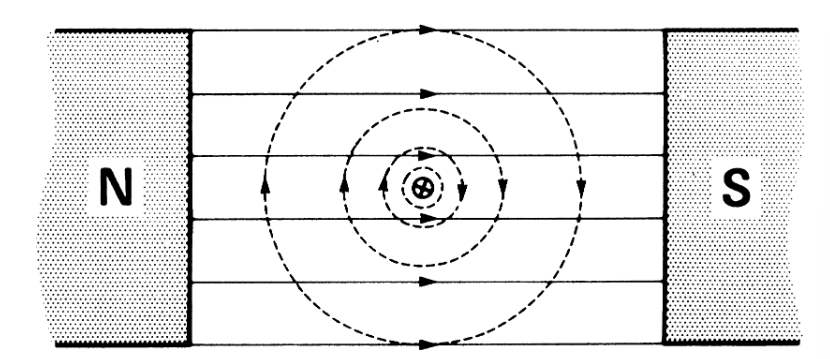
שדה מגנטי כתוצאה ממגנט ומוליך. (Wildi, 2014).

האיור לעיל מציג גם את השדה המגנטי הנוצר בין הקטבים ו- של מגנט קבוע.
כמובן שלשדה המגנטי אין את הצורה המוצגת באיור לעיל כי הקווים של שדה מגנטי אף פעם לא חותכים אחד את השני. למעשה, הקווים שנוצרו ע”י המוליך והמגנט הקבוע פועלים באותו הכיוון מעל המוליך ובכיוונים הפוכים מתחתיו. לפיכך, מספר הקווים מעל המוליך חייבים להיות גדול יותר ממספר הקווים מתחתיו. נקבל את השדה:

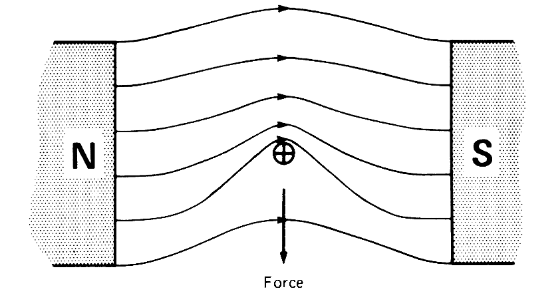
השדה המגנטי האמיתי כתוצאה ממגנט קבוע ומוליך. נשים לב שהוא דוחף את המוליך כלפי מטה. (Wildi, 2014).

ניתן לחשוב על קווי השטף כרצף של גומיות אלסטיות. לכן, אפשר לראות שישנו כוח הפועל על המוליך כלפי מטה.

צפיפות שטף שיורית וכוח כַּפְיָנִי

הביטו בסליל הבא, המקיף חומר מגנטי בצורת טבעת:

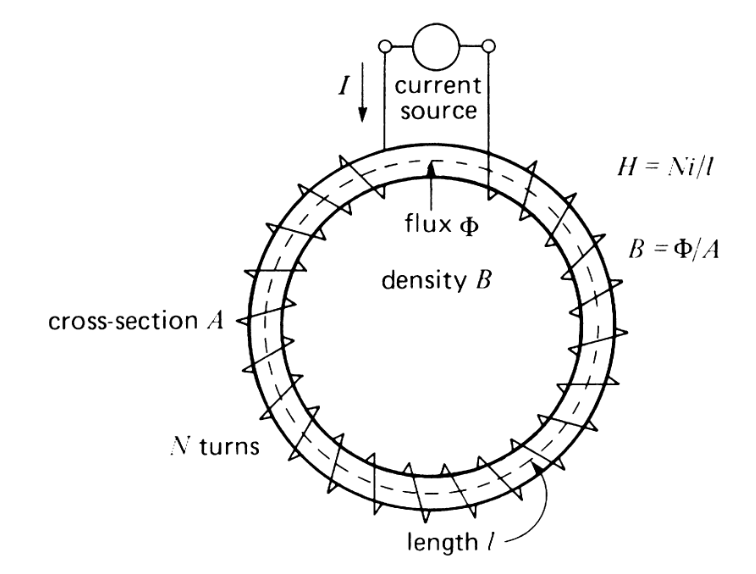
אופן חישוב מאפייני ה- של חומר מגנטי. (Wildi, 2014).

מקור זרם, המחובר לסליל, יוצר זרם שערכו וכיוונו ניתנים לשינוי כרצוננו. ככל שנגדיל את הזרם מאפס, ו- גדלים. עלייה זו יוצרת את עקומה בגרף הבא:

השראות שיורית כוח כפייני. (Wildi, 2014).

צפיפות השטף מגיעה לערך לעוצמת שדה מגנטי . כעת, אם ננמיך את הזרם באופן איטי בחזרה לאפס, צפיפות הזרם לא חוזרת על אותה העקומה, אלא היא נעה לאורך שנמצא מעל . תאכלס תאכלס, כאשר אנו מקטינים את עוצמת השדה המגנטי, התחום המגנטי שהתיישר כתוצאה מ- נוטה להישאר בכיוון זה. לתופעה זו קוראים הִיסְטֵרֵזָה (hysteresis). כתוצאה מכך, כאשר קטן לאפס, צפיפות שטף משמעותית נשארת. קוראים לה צפיפות שטף שיורית, או השראות שיורית (residual induction) .
אם אנו רוצים לבטל את השטף השיורי הזה, אנו חייבים להפוך את כיוון הזרם בסליל ולאט לאט להגדיל את בכיוון ההפוך. כאשר אנו עושים זאת, אנו נעים לאורך העקומה . התחומים המגנטיים משנים את הכיוון שלהם כתוצאה מכך, עד שצפיפות הזרם המגנטי מתאפסת בנקודה . עוצמת השדה המגנטי הנדרשת לבצע זאת נקראת כּוֹחַ כַּפְיָנִי(coercive force).
בהקטנת צפיפות השטף מ- לאפס, אנו צריכים להשקיע אנרגיה. אנרגיה זו נדרשת כדי להתגבר על החיכוך של התחומים המגנטיים כאשר הם מתנגדים לשינוי בכיוון. האנרגיה המושקעת מתפזרת כחום בחומר.

תרגיל 1

נתון המתקן מהצורה של מעגל מגנטי פשוט.

בנוסף נתון כי:

נתון כי פרמיביליות הליבה (היחסית) היא , וגובה מרווח האוויר הוא . אורך ורוחב הליבה כולה הם , ושטח החתך שלה ריבועי עם אורך צלע . בצד ימין של הליבה, שטח החתך שלה מלבני, ומידותיו .

סעיף א’

חשבו את השטף המגנטי.

פתרון:

סכמת הממדים של הבעיה.

כל פעם שיש שינוי בגאומטריה או בחומר, נצטרך לחשב את הרילקטנס בנפרד. כיוון שיש שינוי אחד בחומר (מהליבה לאוויר), ושינוי גיאומטרי יחיד (בצד ימין של הליבה), נוכל לרשום מעגל שקול משלושה רילקטנסים.

מעגל שקול. הוא הרילקטנס של הליבה העבה, של הליבה הדקה יותר, ו- של האוויר.

נשים לב כי:

בנוסף, השטחי חתך הם:

נוכל כעת לחשב את הרילקטנסים (כאשר אנו לוקחים את האורך הממוצע של כל אחד מהקטעים הרלוונטיים):

מהמעגל השקול נסיק שכדי למצוא את הרילקטנס הכולל נוכל פשוט לסכום אותם:

לכן השטף המגנטי:

סעיף ב’

חשבו את השטף המגנטי בהזנחת התנגדות הליבה.

פתרון:
המעגל כעת הוא:

המעגל בהזנחת התנגדות הליבה.

השטף מוגבל אך ורק ע”י מרווח האוויר:

בהשוואה לסעיף א’, יש לנו שגיאה של כ- כתוצאה מההזנחה.

סעיף ג’

חשבו את צפיפויות השטף במרכז הסליל ובמרווח האוויר.

פתרון: