PHY1_006 כוחות משמרים שימור אנרגיה מכנית, הספק

→ קודם: PHY1_005הבא: PHY1_007 ←

כוחות משמרים

נניח גוף בעל מסה הנע בהשפעת הגרביטציה בלבד מנקודה לנקודה . לגוף יש מהירות התחלתית והמרחק בין הנקודות הוא . נניח שבנקודה הגוף נעצר. מהי העבודה שעשה כוח הגרביטציה במהלך תנועת הכדור?

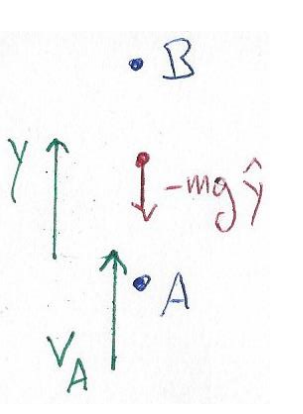
מכיוון שלגוף יש מסה, פועל עליו כוח גרביטציה בכיוון השלילי של ציר ה- שבחרנו. גודל הכוח הוא . נצפה שהעבודה שהגרביטציה עושה היא שלילית כי הכוח פועל נגד כיוון הגוף. מכיוון שזאת בעיה חד ממדית:

כאשר בשתי השוויונות האחרונים השתמשנו במשפט העבודה אנרגיה ובכך שאין לגוף אנרגיה קינטית בנקודה . מצאנו כי . שימו לב שהעבודה שעשתה הגרביטציה תלויה רק בנקודה ההתחלתית והסופית של התנועה.

נשים לב שניתן לחשב בנפרד את העבודה שעושה כל כוח הפועל על גוף. בדוגמא זו אני, גידי, ארים גוף מנקודה לנקודה . נניח כי אין לגוף מהירות ב או ב . במקרה זה הכוח שאני מפעיל פועל נגד הגרביטציה ולכן פועל בכיוון התנועה. מכאן שהעבודה הכוללת שלי ושל הגרביטציה היא:

אנו רואים שהעבודה שאני עשיתי היא .
יש כאן שתי תוצאות מעניינות. הראשונה היא שהעבודה הכוללת היא זה משקף שאין שינוי באנרגיה הקינטית. השנייה היא שהעבודה שעשתה הגרביטציה תלויה רק בנקודה ההתחלתית והסופית של התנועה. בואו נראה אם זה נכון באופן כללי. נעשה דוגמא תלת ממדית עבור גרביטציה.

נביט בדוגמה:
נגדיר את הפרש הגבהים בין שתי נקודות כ- . במקרה התלת ממדי הכללי, נאפשר לגוף לנוע באיזשהו מסלול אקראי. הגרביטציה לבד לא יכולה לגרום לגוף לנוע כך, חייב להיות עוד כוח, אך בדוגמא זאת נחשב רק את העבודה הנעשית על ידי הגרביטציה.

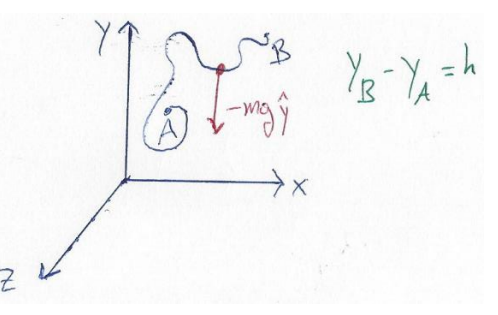
במקרה זה , וגם . מכאן שהעבודה שעושה כוח הגרביטציה:

כאשר השתמשנו בכך שהכוח פועל רק בכיוון , ובכך שהסכימה על כל העתקים בכיוון בין ל- מסתכמים להפרש הגבהים בין הנקודות.

אנו רואים שהעבודה שעשתה הגרביטציה אינה תלויה במסלול שהגוף עשה. לא משנה עד כמה המסלול משוגע, כל מה שמשנה הוא הפרש הגבהים, , בין הנקודות ו-. לכן, הגרביטציה היא כוח משמר:

כוח משמר

הגדרה:

כאשר העבודה הנעשית על ידי כוח אינה תלויה במסלול, אלא נקבעת רק על ידי נקודת ההתחלה והסוף, כוח זה נקרא כוח משמר.

באופן כללי, עבור תנועה בהשפעת הגרביטציה בלבד, ניתן להפעיל את משפט העבודה אנרגיה. במקרה זה העבודה הנעשית בלהגיע מנקודה A לנקודה B היא (לפי משפט העבודה אנרגיה):

נסדר את הביטויים מחדש ונקבל:

נוסחה:

אנו קוראים ל האנרגיה הפוטנציאלית הגרביטציונית ומסמנים אותה באות . מכאן שהסכום של האנרגיה הפוטנציאלית הגרביטציונית והקינטית נשמר:

ניתן להעביר סוג אחד של אנרגיה לסוג השני - קינטית לפוטנציאלית ולהיפך – אך הסכום חייב להישמר. שימו לב שבגלל שהפעלנו את משפט העבודה אנרגיה, שנכונה רק עבור העבודה שעשה שקול הכוחות, השימור של סכום האנרגיה הפוטנציאלית הגרביטציונית והאנרגיה הקינטית נכון עבור תנועה בהשפעת כוח הכבידה בלבד.

גם כוח הקפיץ הפועל לפי חוק הוק הוא חוק משמר:

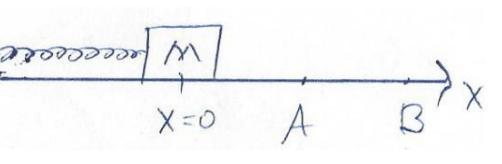
כפי שאנו רואים, העבודה שעושה הקפיץ תלויה רק בנקודת ההתחלה והסוף של התנועה. לכן גם הכוח שמפעיל קפיץ אידיאלי (חוק הוק) הוא חוק משמר. מכאן שניתן להגדיר מערכת של קפיץ אנרגיה פוטנציאלית .

אנרגיה מכנית

כוח מכני

הגדרה:

כוח מכני הוא כוח הגורם לתנועת גוף.

דוגמאות לכוחות מכניים הם הגרביטציה וכוח הקפיץ. אם כל הכוחות בבעיה נתונה הם מכניים ומשמרים, אז ניתן להגדיר עבורם פונקציית פוטנציאל .

אנרגיה מכנית

הגדרה:

הסכום נקרא אנרגיה מכנית. תכיל את סכום האנרגיות הפוטנציאליות של כל הכוחות המשמרים במערכת (גרביטציה, קפיץ ועוד).

שימור אנרגיה מכנית

אם כל הכוחות בבעיה הם מכנים ומשמרים, אז מתקיים חוק שימור האנרגיה המכנית:

משפט:

זו הסיבה שכוחות אלו נקראים כוחות משמרים. תוצאה זאת מאוד שימושית. נשתמש בה לעיתים קרובות, אך צריך להיזהר ולבדוק שכל הכוחות בבעיה הם משמרים (ניתן לראות שזה תנאי הכרחי כי הביטוי תלוי רק בנקודת ההתחלה והסוף). אנרגיה קינטית ופוטנציאלית הם מספרים הניתנים למערכת המקיימים את חוק השימור (אם כל הכוחות הם משמרים). באופן כללי, אנרגיה פוטנציאלית מתייחסת לסידור הגופים במרחב.

כוחות לא משמרים

האם כל כוח הוא משמר? התשובה היא לא. לדוגמא, חיכוך אינו כוח משמר. לשם הדגמה נזיז גוף, למשל המחק של הלוח, בין שתי נקודות. במקרה זה כוח החיכוך עושה עבודה שלילית כי הוא תמיד מכוון נגד כיוון התנועה. אני, הדוחף את המחק, עושה עובדה חיובית. אם נזיז את המחק בין אותן שתי נקודות אך במסלול יותר ארוך, העבודה שהחיכוך תעשה היא שלילית יותר כי כיוון הכוח תמיד נגד כיוון התנועה. הכוח שאני אעשה יהיה גדול יותר, כי הכוח תמיד בכיוון התנועה. מכיוון שהעבודה של כוח החיכוך אינה תלויה רק בנקודה ההתחלתית והסופית, הוא אינו כוח משמר.

נראה זאת באופן מפורש: כוח החיכוך מנוגד לתנועה היחסית בין המשטחים. בנוסף, בהנחה שאני לוחץ את המחק על הלוח באופן אחיד לאורך התנועה, אז גודל כוח החיכוך הקינטי הוא קבוע. עבור תנועת המחק על השולחן הזווית בין כוח החיכוך להעתק האינפיטיסמלי הוא ולכן:

נחשב את העבודה שעושה כוח החיכוך במקרה זה:

כאשר בשוויון השלישי השתמשנו בכך שהסכום של גודל ההעתק האינפיניטסימליים לאורך המסלול הוא אורך המסלול, .

נוסחה:

נשים לב שכל עוד , כלומר כל עוד המחק נע לאורך מסלול, עבודת החיכוך תמיד שלילית! גם אם הוא חזר לאותה הנקודה! לא היה לנו את מצב זה בכוח הגרביטציה - אם כדור נופל העבודה שהכוח מבצע היא שלילית, ואם מעלים אותו בחזרה אז העבודה חיובית - מקזזת בחזרה את העבודה שנעשתה כאשר הכדור נפל.

מכאן שכוח החיכוך תלוי באורך המסלול, , ולא רק בנקודת ההתחלה והסוף. אלו היינו בוחרים מסלול בעל אורך אחר, העבודה של כוח החיכוך לאורך המסלול היה משתנה. כלומר, החיכוך אינו כוח משמר. מכאן שבמערכות הכוללות חיכוך, אין שימור אנרגיה מכנית!

הספק

קבלן רוצה להרים חומרי בניין מהמדרכה לראש בניין בעזרת מנוף. אנו כעת יודעים לחשב כמה עבודה הכוח המופעל על ידי המנוף יצטרך לעשות. את הקבלן, לעומת זאת, מעניין לדעת את הקצב בה העבודה נעשית. האם העבודה תיקח 5 דקות או שבוע.

הגדרה:

הקצב בה העבודה נעשית נקראת הספק של הכוח. אם העבודה, , נעשית על ידי כוח בזמן , ההספק הממוצע בפרק זמן זה הוא:

וההספק המיידי )מה שבדרך כלל נקרא הספק) הוא:

יחידות:

ניתן לבטא את ההספק שכוח עושה על גוף בעזרת הכוח ומהירות הגוף:

כאשר הנחנו שהכוח אינו תלוי בזמן. במקרה התלת ממדי נקבל:

→ קודם: PHY1_005הבא: PHY1_007 ←