מבוא
כעת נעסוק בבעיות תלויות בזמן דרך משוואות האלסטודינמיקה עבור עיוותים אינפיניטסימליים:
צעידה בזמן כללית
כדי להמחיש את תהליך הצעידה בזמן, נתחיל עם הדינמיקה של מסה נקודתית בודדת תחת השפעת כוח
כאשר
ועבור
חיסור שני הביטויים נותן:
כאשר
נשים לב שסכום משוקלל של משוואות (ZT9.3) ו-(ZT9.4) נותן:
ביטוי זה יהיה שימושי בהמשך. כעת נפתח את מיקום המסה בטור טיילור סביב
ו-
חיסור שני הביטויים נותן:
הצבת משוואה (ZT9.7) נותנת:
ושימוש במשוואה (ZT9.6) נותן:
הביטוי
הערות:
- כאשר
, זוהי שיטת אויילר לאחור (Backward Euler) הסתומה, שהיא מאוד יציבה ו- באופן מקומי בזמן. - כאשר
, זוהי שיטת שיטת אויילר לפנים (Forward Euler) המפורשת, שהיא יציבה בתנאים מסוימים ו- באופן מקומי בזמן. - כאשר
, זוהי שיטת “נקודת האמצע” (Midpoint) הסתומה, שהיא יציבה ו- באופן מקומי בזמן.
לסיכום, קיבלנו עבור המהירות1:
ועבור המיקום:
או במונחים של
יישום לנוסח הרציף
כעת נתבונן באנלוגיה הרציפה ל-"
כאשר הסימון העליון
בהנחה ואנו מקרבים את הפתרון ע”י
לאחר העברת אגפים:
נרשום את אותה המשוואה לאחר צעד זמן
נכפיל את (ZT9.24) במטריצת המסה מצד שמאל:
נציב ב-(5.3) את (5.1) ו-(5.2):
לאחר העברת אגפים:
נסמן:
ונסכם:
יציבות בזמן
כפי שהוצג בקטע הקודם, שיטת אוילר לפנים לא תמיד יציבה. כלומר, אם נבחר
כאשר
דרך יותר שיטתית המפורטת ב-(Surana & Reddy, n.d.) שיותר נוח לממש אותה ב-MATLAB היא לחשב את הע”ע המקסימלי של
בעיות הולכה בזמן
נפתח כעת הצורה החלשה של בעיות הולכה בזמן. במקרה החד-ממדי, לפי משוואת החום החד-ממדית:
בקורס אנו נכתוב את משוואה זו בצורה טיפה שונה. במידה ושטח החתך או הקבוע הולכה לא אחידים, אז יש לנו את הגרסא היותר כללית:
לאחר טיפה העברת אגפים:
נסמן
כאשר
נקרב את
לפי שיטת גלרקין, ולאחר אינטגרציה בחלקים:
נוכל לרשום באופן מטריצי:
כאשר:
תרגילים
שאלה 1
בהינתן הבעיה התלויה בזמן הבאה (בעיית חום):
פתרו את הבעיה עבור הפרש סופי יחיד באורך
- עבור
- עבור
- עבור
פתרון עבור
לפי בעיות הולכה בזמן, הצורה החלשה של הבעיה:
עם
לפי (5.8), כאשר נשים לב ש-
נחשב כל אחד מהמטריצות:
נשים לב ש-
עבור
נפעיל את תנאי השפה
במצב התחלתי, לפי תנאי ההתחלה:
נחשב את הערך של
לאחר צעד אחד של
כלומר:
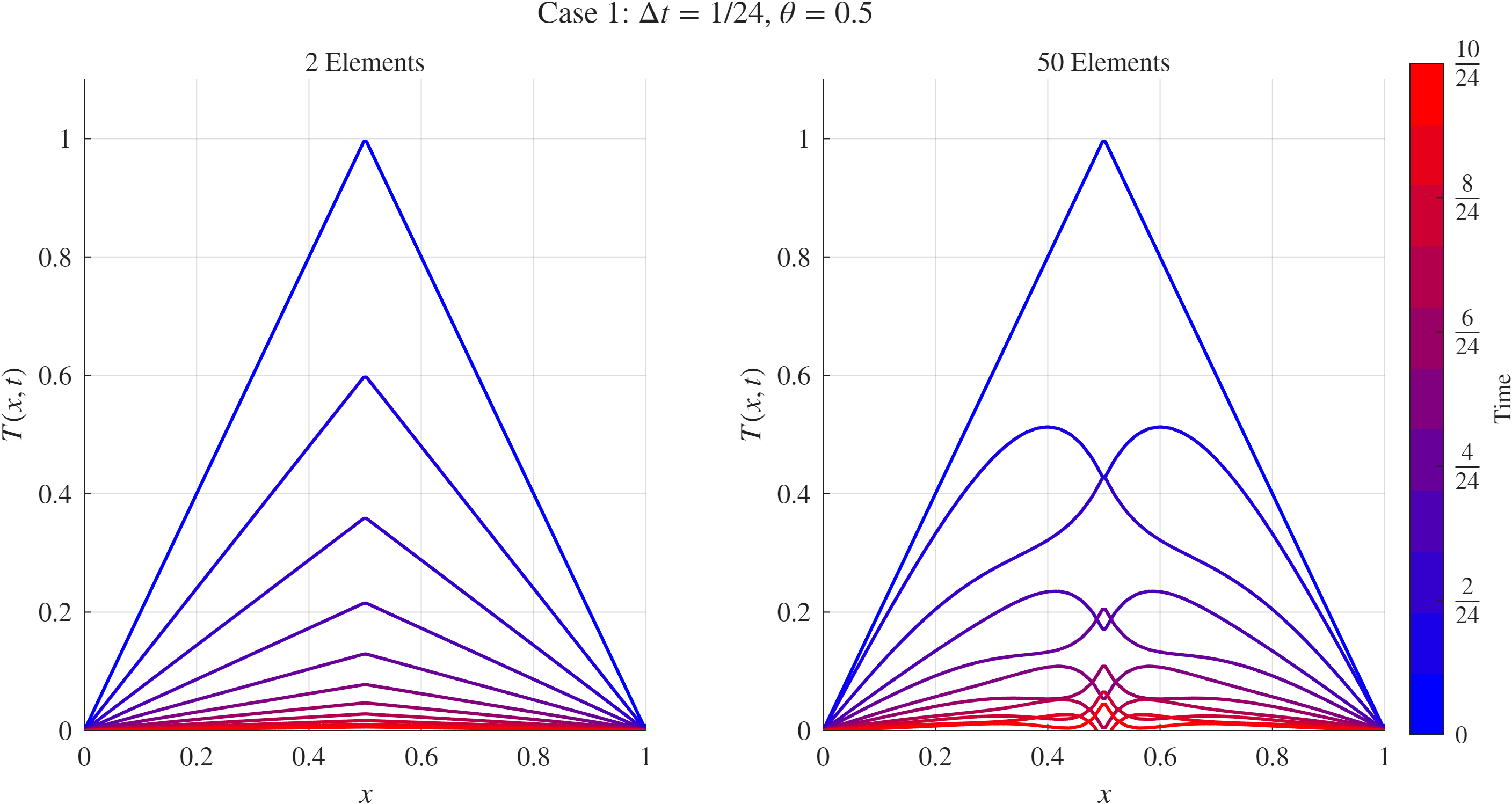
פתרון פילוג הטמפרטורה עבור קפיצות זמן די גסות.
פתרון עבור
עבור
בהתחשב בתנאי השפה, נקבל:
ולכן:
לאחר צעד אחד של
כלומר:
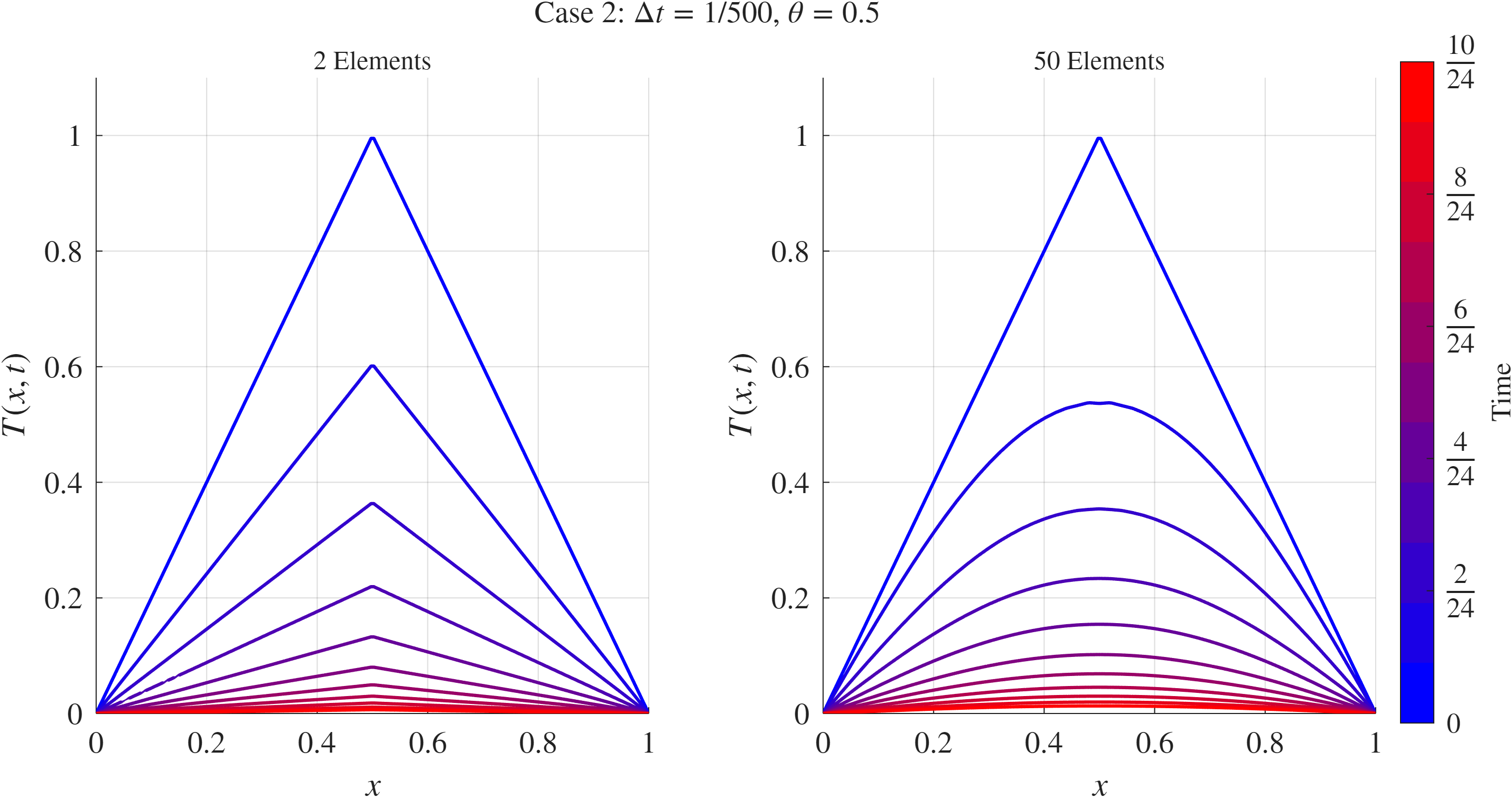
פתרון פילוג הטמפרטורה עבור קפיצות זמן עדינות.
פתרון עבור
עבור
בהתחשב בתנאי השפה ועבור
ולכן:
לאחר צעד אחד של
כלומר:
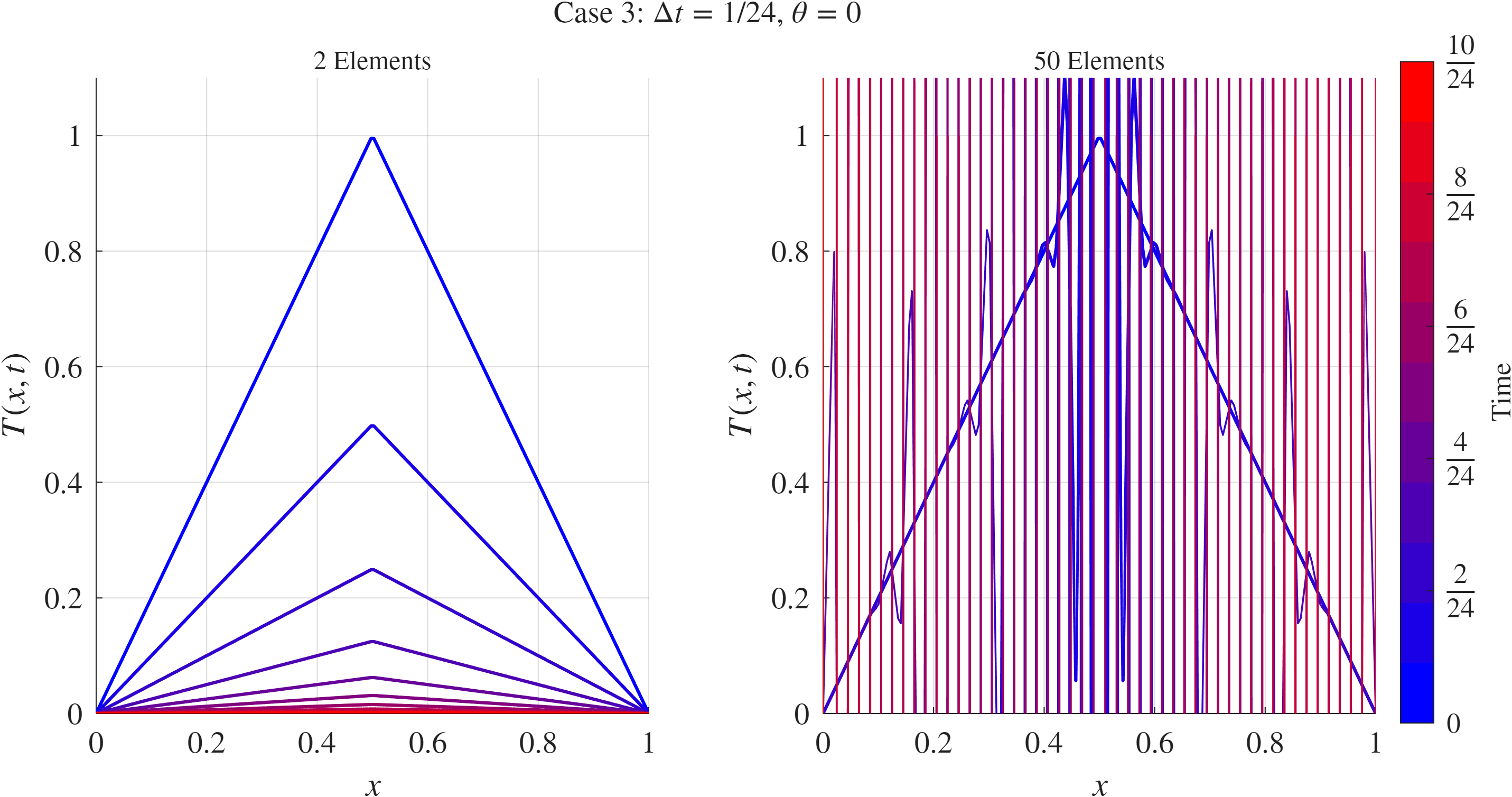
פתרון פילוג הטמפרטורה עבור שיטת אוילר לאחור. כפי שניתן לראות, היא לא בהכרח יציבה.
נוכל למצוא קריטריון ליציבות בזמן של הפתרון בעזרת המטריצה
עבור המקרה של
כלומר, יש לנו מקרה פשוט שהמטריצה שלנו היא ערך יחיד. הע”ע שלנו הוא פשוט
כך שעבור שני אלמנטים,
כלומר, ככל שיש יותר אלמנטים (דיסקרטיזציה עדינה יותר במרחב), קריטריון היציבות נעשה מחמיר יותר, ונדרש לבחור
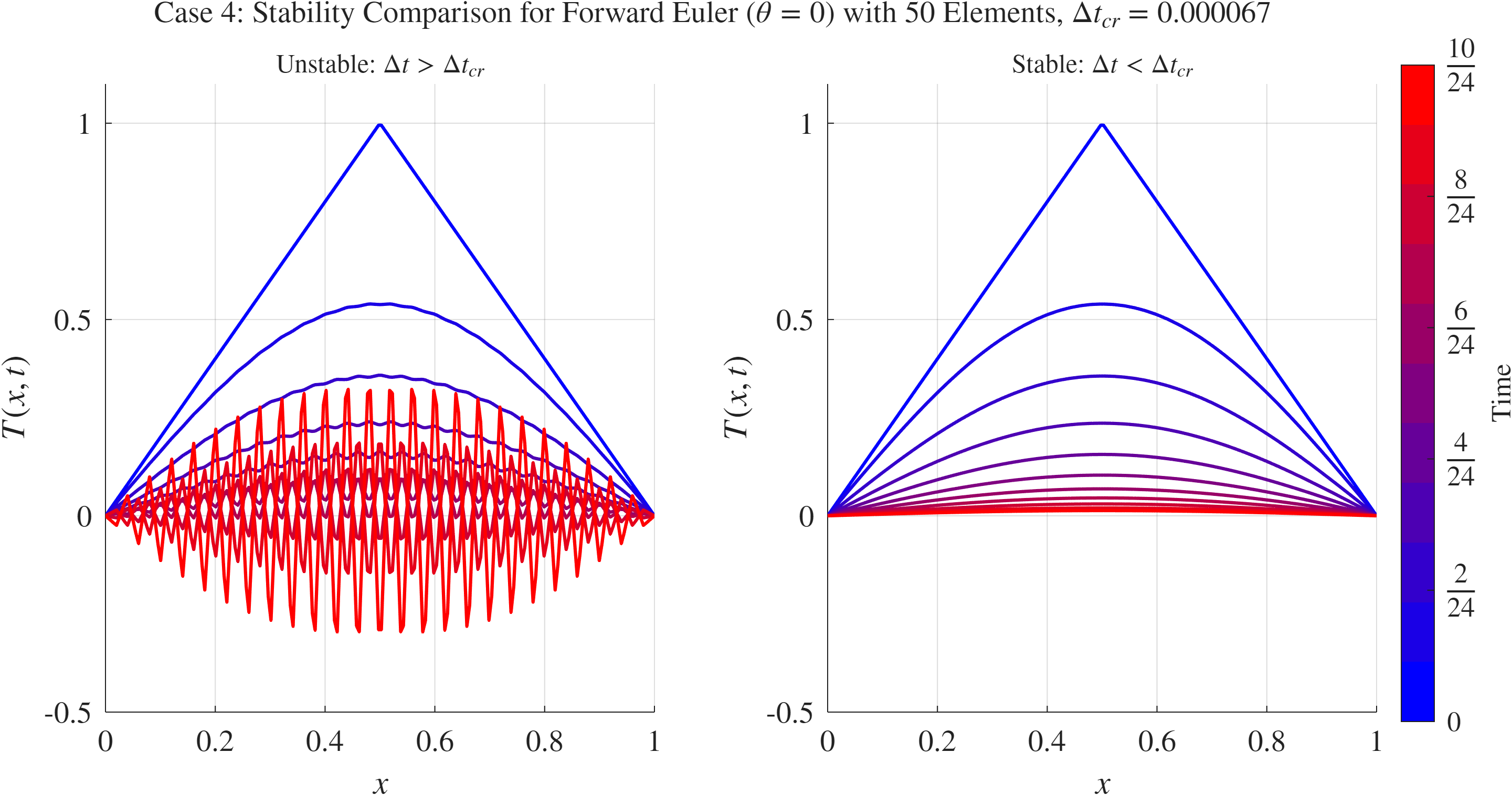
השוואה בין צעידה זמן גדולה מהערך הקריטי ליציבות לצעידת זמן קטנה יותר מהערך הקריטי ליציבות.
הערות שוליים
-
לצורך פישוט הסימון, אנו משמיטים את הביטויים
