FEM1_006 שיטת אלמנטים סופיים בתלת-ממד

→ קודם: FEM1_005הבא: FEM1_007 ←

מבוא

אף על פי שיש בכך חזרתיות מסוימת, אנו עוקבים אחר פיתוח דומה לזו שנעשתה בניתוח החד-ממדי בפרקים הקודמים. כדי לגזור צורה חלשה ישירה עבור גוף, אנו לוקחים את מאזן התנע הקווי (המציין את הצורה החזקה) ויוצרים מכפלה סקלרית עם פונקציית וקטור חלקה שרירותית , ומבצעים אינטגרציה על פני הגוף,

כאשר הוא השארית ו- היא פונקציית מבחן.

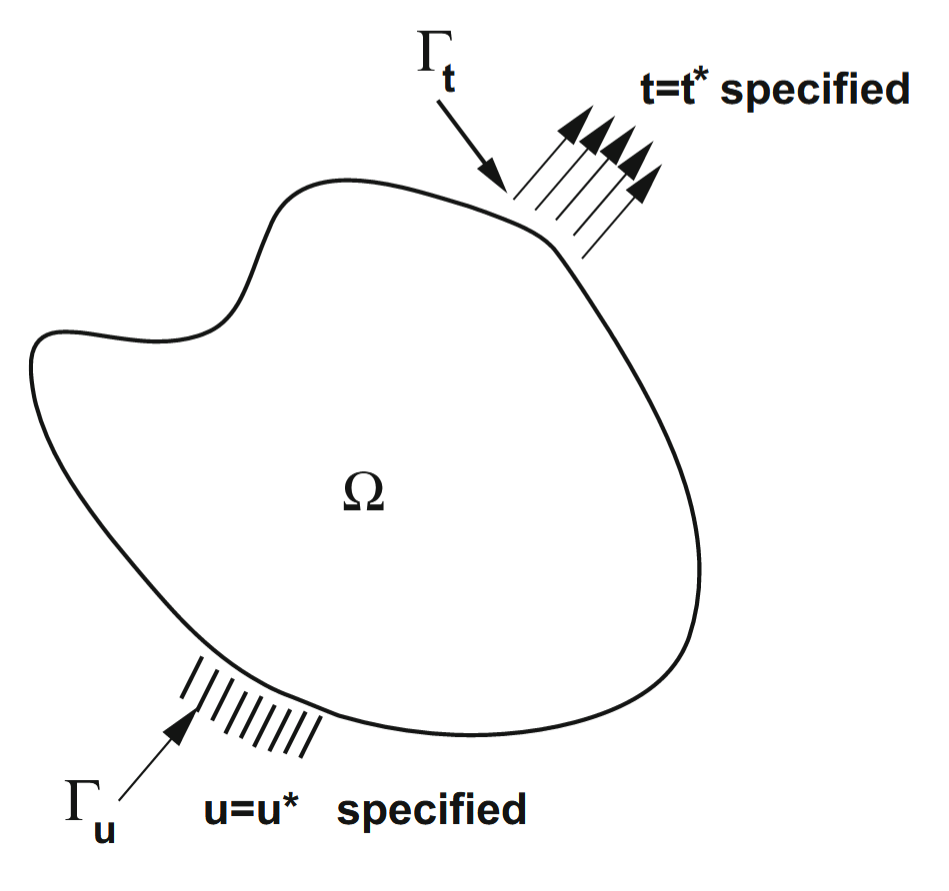
תפוח אדמה הנדסי. (Zohdi, 2018).

אם נוסיף תנאי שאנו עושים זאת עבור כל פונקציות המבחן האפשריות (), משוואה (ZT6.1) מרמזת ש- . לכן, אם כל פונקציית מבחן אפשרית נלקחה בחשבון, אז

על כל אזור סופי ב-. כתוצאה מכך, ההצהרות החלשות והחזקות יהיו שקולות בהינתן שהפתרון האמיתי חלק מספיק כדי שיהיה לו פתרון חזק. ברור ש- לעולם לא יכול להיות שונה מאפס על פני אזור סופי כלשהו בגוף, מכיוון שפונקציית הבדיקה תאתר אותם. באמצעות כלל המכפלה של נגזרת,

מוביל ל-,

כאשר אנו בוחרים את מתוך קבוצה קבילה, שנדון בה בהמשך. באמצעות משפט גאוס, אנו מגיעים ל-,

אשר, מכיוון שההטרחה , מוביל ל-

מתקיים גם , שזה תאכלס קשרי מאמץ עיבור לחומר כללי. הוא טנזור הקשיחות מסדר רביעי, שבמוצקים ראינו אותו עם כל השאלות המעצבנות על , או את ההופכי שלו, .

למה ? זה לא אמור להיות ?

תאכלס כן, לא הכי נכון כאן לרשום , אבל עם איך שנרשום את בהמשך, ועם איך שנבצע עליו גזירה (בעזרת טנזור דפרומציה ), זה יסתדר.

לפיכך, נוכל לרשום:

אם נחליט להגביל את הבחירות שלנו של לאלה כך ש-, יש לנו,
כאשר הוא התזוזה המוחלת על , עבור אלסטיות ליניארית עם עיבור אינפיניטסימלי, הבעיה בצורתה החלשה היא:

מצאו , , כך ש-, :

כאשר על .

כמו בניסוח החד-ממדי, זה נקרא “צורה חלשה” מכיוון שהיא אינה דורשת את הגזירות של המאמץ . במילים אחרות, דרישות הגזירּות נחלשו. נדגיש שאם נבדוק את הפתרון עם כל פונקציות המבחן האפשריות של חלקות מספקת, אז הפתרון החלש שקול לפתרון החזק. יתר על כן, בהינתן שהפתרון האמיתי חלק מספיק, הצורות החלשה והחזקה הן שקולות.

מרחבים סובולב הילברטיים

כמו בממד אחד, אחת משאלות המפתח היא בחירת פונקציות הבסיס בצורה החלשה. באופן נאיבי למדי, התשובה פשוטה - האינטגרלים חייבים להישאר סופיים.

באותו אופן כמו בחד-ממד, אנו מגדירים את כמרחב של פונקציות וקטוריות שרכיביהם ב- , כלומר:

לפיכך, אנו מנסחים את הבעיה החלשה בצורה הבאה:

מצאו , , כך ש-, :

קירוב אלמנטים סופיים (FEM)

נוח לרשום את התבנית הבילינארית בצורה מטריציונית באופן הבא:

כאשר , טנזור הדפורמציה (עיבור), מוגדר כ (לפי סימון Voigt):

את טנזור הקשיחות נרשום באופן מטריצי. עבור חומר אלסטי ליניארי תלת-ממדי כללי, טנזור הקשיחות הוא מסדר רביעי, אך ניתן לייצגו כמטריצה סימטרית בגודל (סימון Voigt):

במקרה של חומר איזוטרופי, המטריצה הזו מקבלת צורה פשוטה יותר, עם שני פרמטרים בלתי תלויים: מודול האלסטיות ומקדם פואסון (בלי קשר לפונקציית הבוחן ). מטריצת הקשיחות עבור חומר אלסטי ליניארי איזוטרופי תלת-ממדי ניתנת על ידי:

סימון Voigt ניתן להרחבה גם לגדלים נוספים שדנו בהם, כגון וקטור המאמץ ווקטור העיבור , כך שבסימון מטריצי:

ברור שבמימוש שיטת האלמנטים הסופיים, יש לקחת בחשבון את דלילות המטריצה (כלומר, העובדה שהיא מכילה אפסים רבים - sparse). כמו כן, נוח לרשום את הקירובים כך:

או , כאשר, לדוגמה¹:

נוח לרשום:

וכן . אם נבחר את עם אותו בסיס, אך עם צירוף לינארי שונה , אז נוכל לכתוב:

מכיוון ש- שרירותי (כלומר ), נקבל:

באופן מפורש, היא מערכת המשוואות שיש לפתור.

טרנספורמציות גלובליות/מקומיות

אחת החוזקות של שיטת האלמנטים הסופיים היא שרוב החישובים יכולים להתבצע באופן פרטני לכל אלמנט (element-by-element). אנו מגדירים את איברי :

וכן

בפירוק החישובים לאלמנטים, , כאשר (מספר האלמנטים), כאשר

וכן

כאשר וכן . על מנת להפוך את החישובים לשיטתיים, אנו מעוניינים להשתמש באלמנט הכללי או “אלמנט המסטר” המוגדר במערכת קואורדינטות מקומית . בהתאם לכך, אנו זקוקים לפונקציות המיפוי הבאות, מקואורדינטות האלמנט הכללי לקואורדינטות במרחב האמיתי, (לדוגמה, אלמנטים תלת-לינאריים):

כאשר הן הקואורדינטות המרחביות האמיתיות של הצומת ה-, וכן . בדומה למקרה החד-ממדי, מיפויים מסוג זה נקראים בדרך כלל מיפויים פרמטריים. אם סדר הפולינום של פונקציות הצורה גבוה כמו זה של האלמנט, זהו מיפוי איזופרמטרי; אם נמוך יותר, תת-פרמטרי; ואם גבוה יותר, סופר-פרמטרי.

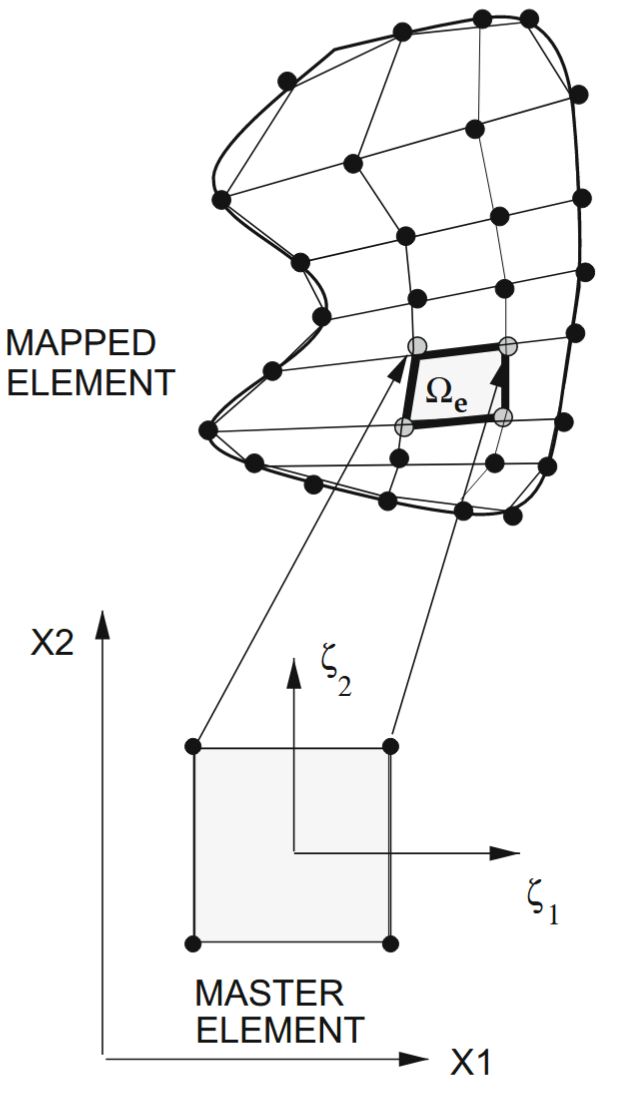
אלמנט סופי דו-ממדי. (Zohdi, 2018).

יצירת רשת ופונקציות קישוריות

כדי לקשר בין המספור המקומי של הצמתים למספור הגלובלי, נדרשת שיטה פשוטה לאוטומציה של תהליך זה. עבור גאומטריות מסובכות, יש צורך במערך חיפוש (lookup array) המקשר בין מספר הצומת המקומי בתוך אלמנט למספר הגלובלי. חיבור גלובלי/מקומי חשוב מכיוון שמיקומם הנכון (הגלובלי) של האיברים במטריצת הקשיחות נדרש בעת פתרון מערכת המשוואות, בין אם על ידי אלימינציית גאוס או בכפל אלמנט-אחר-אלמנט בשיטת פתרון מסוג Conjugate Gradient (CG).

מספר אלמנט	צומת גלובלי 1	צומת גלובלי 2	צומת גלובלי 3	צומת גלובלי 4
1	1	2	3	4
2	2	3	4	5
3	7	8	9	10
4	6	7	8	9

מספור גלובלי של צמתים עבור אלמנטים לדוגמה של קשת. כל שורה מייצגת אלמנט, והעמודות מייצגות את מספרי הצמתים הגלובליים המרכיבים אותו לפי סדר מקומי (צומת מקומי 1, 2, 3, 4). מספור זה הוא עבור המיפוי באיור הבא.

מגבלות על אלמנטים

נזכיר שבחד-ממד יש לנו חישוב מהסוג הבא:

ברור שיעקוביאן אפס יוביל לבעיות ולאינטגרלים שעלולים להיות סינגולריים. בחד-ממד, היה קל להימנע מכך מכיוון שהצמתים ממוספרים באופן סדרתי, וכל עוד הצמתים אינם מתלכדים, הדבר לא יקרה, מאחר ש-. עם זאת, ברור ש- אינו פיזיקלי, מכיוון שמשמעותו היא שצמתים שכנים ממופים ‘הפוך’ (אחד דרך השני). יעקוביאנים שליליים יכולים גם להוביל למטריצות קשיחות לא מוגדרות (indefinite). כמו בניסוחים חד-ממדיים, בניסוחים דו-ממדיים ותלת-ממדיים, יש לוודא ש- בכל התחום. ישנן שתי דרכים שבהן יכולים להיווצר יעקוביאנים לא-חיוביים: (ZT1) האלמנטים אינם קמורים (non-convex) ו-(2) מספור הצמתים שגוי, מה שגורם לאלמנטים ‘להימשך הפוך’. עלינו להבטיח ש-, מכיוון של- יש משמעות פיזיקלית: הוא היחס בין הנפח הדיפרנציאלי של אלמנט המסטר לנפח הדיפרנציאלי של האלמנט הסופי. אם הצמתים ממוספרים נכון כדי להבטיח שהם לא ‘נמשכים הפוך’ (לדוגמה, ראו את האיור הבא) ושהאלמנטים קמורים, אז .

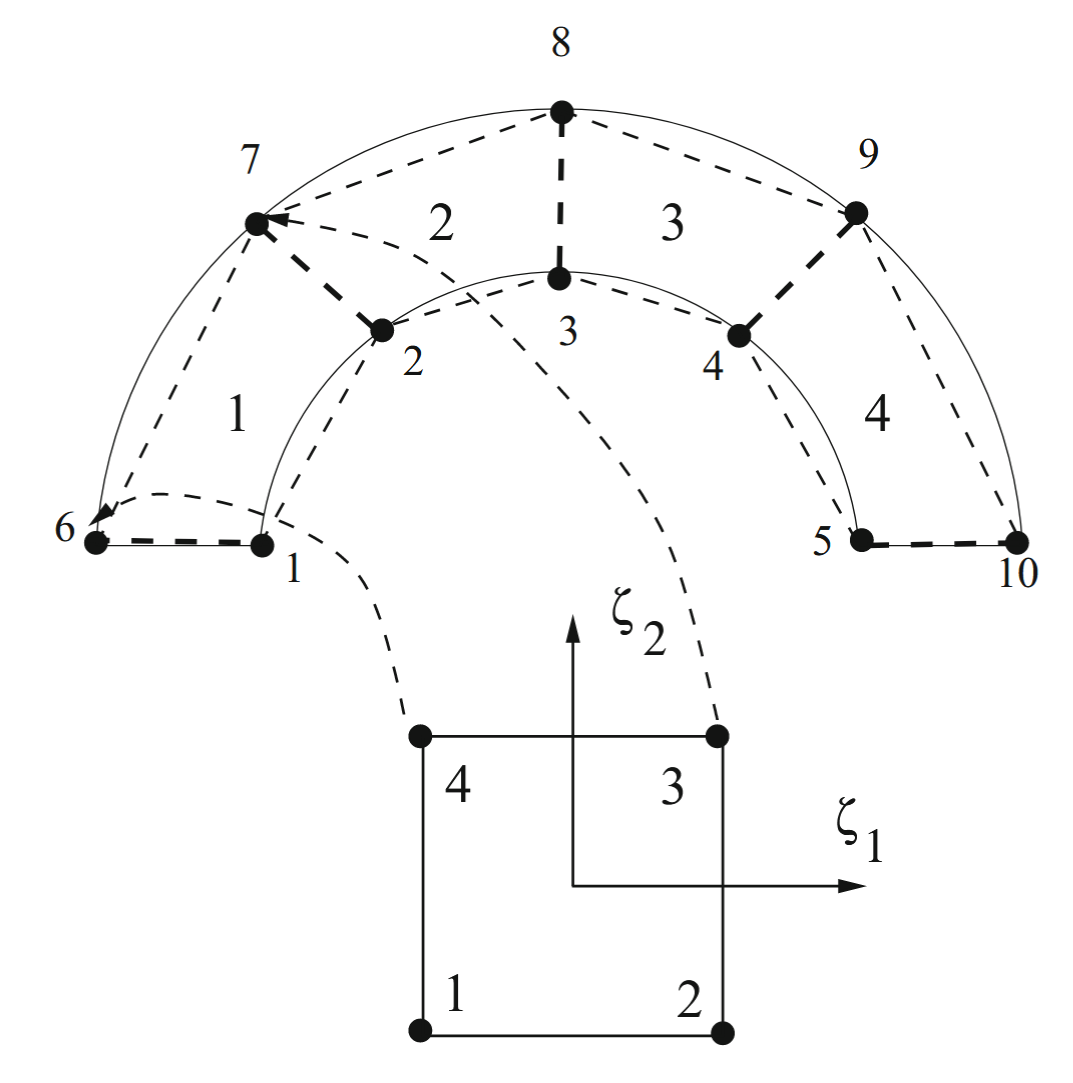
דוגמה לרשת ממופה עבור רצועה חצי מעגלית.

אלמנטים טובים ורעים: דוגמאות

נתבונן באלמנט לינארי דו-ממדי. פונקציות הצורה הן:

פונקציות המיפוי הן:

כאשר הן הקואורדינטות המרחביות האמיתיות של הצומת ה-, וכן . נבחן ארבע דוגמאות. כדי שהאלמנטים יהיו קבילים, היעקוביאן המתאים לטרנספורמציה חייב להיות חיובי וסופי בכל האלמנט, כאשר:

באופן מפורש:

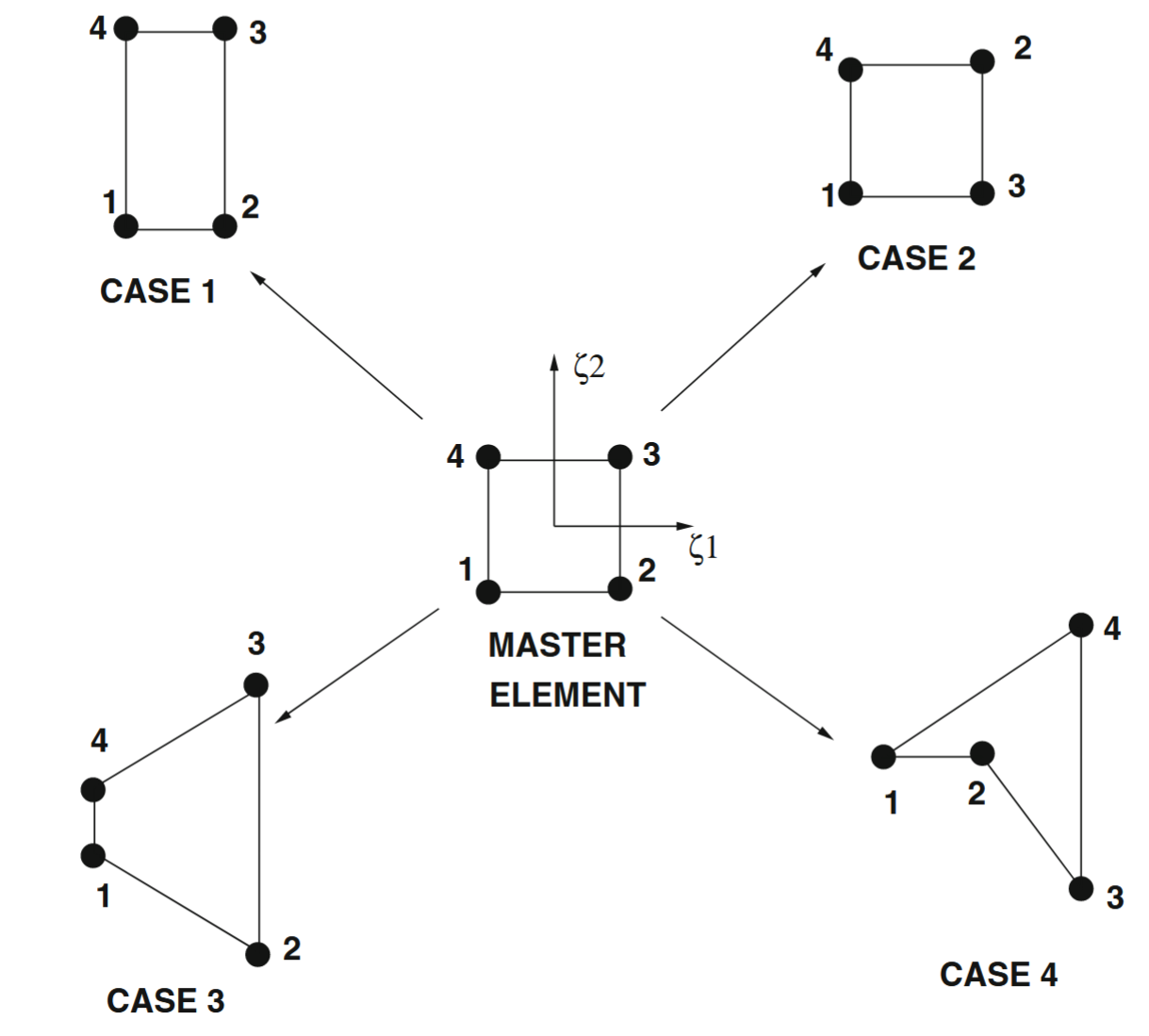
אלמנט לינארי דו-ממדי ודוגמאות למיפוי. (Zohdi, 2018).

עבור ארבעת המקרים באיור לעיל, יש לנו:

• מקרה 1: אלמנט זה קביל, מאחר ש- בכל האלמנט. היעקוביאן קבוע במקרה זה.
• מקרה 2: אלמנט זה אינו קביל, מאחר ש- בכל האלמנט. הבעיה המהותית היא שהצמתים ממוספרים באופן שגוי, מה שהופך את האלמנט ל-‘הפוך’.
• מקרה 3: אלמנט זה קביל, מאחר ש- בכל האלמנט. בעוד שהיעקוביאן אינו קבוע בכל תחום האלמנט, הוא חיובי וחסום.
• מקרה 4: אלמנט זה אינו קביל, מאחר ש- באזורים מסוימים של האלמנט. למרות שהיעקוביאן חיובי בחלקים מסוימים של התחום, יעקוביאן שלילי בחלקים אחרים יכול לגרום לבעיות, כגון סינגולריות פוטנציאלית במטריצת הקשיחות.
• עבור אלמנטים לינאריים, המדד המרכזי לאלמנט בעייתי הוא אי-קמירות (non-convexity) של האלמנט (גם אם הוא ממוספר נכון).

פונקציות צורה תלת-ממדיות

נדגים את בניית שיטת האלמנטים הסופיים עם מה שנקרא אלמנטי “לבנה” (brick) תלת-לינאריים. פונקציות הצורה של האלמנט המסטר יוצרות בסיסים צמתיים של קירוב תלת-לינארי הניתן על ידי:

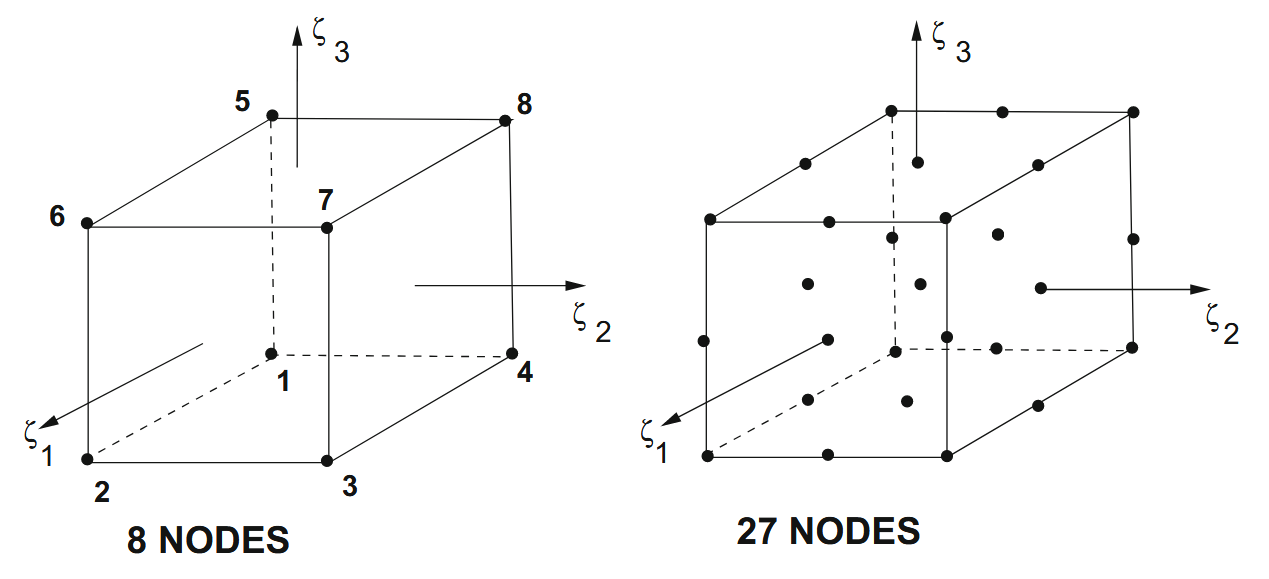
משמאל: משושה תלת-לינארי של שמונה צמתים או “לבנה”. מימין: אלמנט של 27 צמתים. (Zohdi, 2018).

עבור אלמנטים תלת-לינאריים, יש לנו בסיס צמתי המורכב משמונה צמתים, ומכיוון שהוא בעל ערך וקטורי, יש לנו דרגות חופש כוללות (שלוש דרגות חופש עבור כל אחד משמונת הצמתים).

הערה:

עבור אלמנטים ריבועיים סטנדרטיים, יש לנו בסיס צמתי המורכב מ- צמתים (כמו באיור לעיל), ומכיוון שהוא בעל ערך וקטורי, יש לנו דרגות חופש כוללות (שלוש דרגות חופש עבור כל אחד מ- הצמתים).

פונקציות הצורה הצמתיות ניתנות לגזירה באופן קל למדי, על ידי מימוש העובדה שזהו בסיס צמתי, כלומר, הן שוות ליחידות בצומת המתאים, ואפס בכל שאר הצמתים וכו’.

תכונות דיפרנציאליות של פונקציות הצורה

נציין שה- בתחום אינם מחושבים באופן ישיר. אנו מתחילים בפועל עם ה- בתחום המסטר. לפיכך, בחישובי מטריצת הקשיחות והאגף הימני של האלמנטים, כל האיברים חייבים להיות מוגדרים במונחי הקואורדינטות המקומיות. עם זאת בחשבון, אנו מניחים כמה יחסים בסיסיים, הקשורים ישירות למושגי הדפורמציה שהוצגו בדיון שלנו במכניקת הרציפות. גרדיאנט הדפורמציה מופיע שוב בצורה הבאה:

כאשר במפורש:

היחסים הדיפרנציאליים הם:

היחסים הדיפרנציאליים ההפוכים הם:

ולכן:

והצורה ההפוכה:

גזירה בקואורדינטות הייחוס

כעת אנו צריכים לבטא את במונחי , באמצעות:

לפיכך, אנו כותבים עבור העמודה הראשונה² של :

עבור העמודה השנייה:

ועבור העמודה האחרונה:

עבור אלמנט, למטריצת פונקציות הצורה שלנו (מוגדרת כ-) יש את הצורה הבאה עבור פונקציות צורה לינאריות, עבור השמונה עמודות הראשונות:

עבור השמונה עמודות השניות:

ועבור השמונה עמודות האחרונות:

שבסך הכל היא מטריצה בגודל . לכן המכפלה היא מטריצה בגודל בצורה, עבור השמונה עמודות הראשונות:

עבור השמונה עמודות השניות:

ועבור השמונה עמודות האחרונות:

לבסוף, עם ריבוע עבור כל אלמנט, אנו יכולים ליצור כל אחד מתרומות האלמנט עבור :

עבור מטריצת הקשיחות:

כאשר הביטוי הראשון הוא התרומה הסטנדרטית והביטוי השני הוא קנס עבור .

עבור וקטור העומסים:

כאשר וכו’ הם משקלי גאוס וכן מייצג את היעקוביאנים (המשטחיים) של פאות האלמנט על פני השטח החיצוני של הגוף, כאשר, תלוי במשטח שעליו יש להעריך, אחד מרכיבי יהיה או . יעקוביאנים משטחיים אלה ניתנים להערכה במגוון דרכים, לדוגמה באמצעות נוסחת Nanson, שנדונה עוד בקרוב.

יעקוביאנים משטחיים ונוסחת Nanson

על מנת לחשב אינטגרלים משטחיים, עבור אלמנט כללי החותך את המשטח החיצוני, יש לבצע את הפעולות הבאות:

1. זיהוי הפאה המתאימה של האלמנט המסטר שמתאימה למשטח. אחת מקואורדינטות ה- חייבת להיות מוגדרת כ-; כלומר, , , או חייבים להיות שווים ל- עבור הפאות המתאימות למשטחים החשופים על הגוף שבהם מוחלים תנאי השפה.

   באופן כללי, אנו מעוניינים לבצע אינטגרציה של כמות על פני השטח של האלמנט האמיתי, המעוות, על ידי חישוב על פני האלמנט המסטר, שעבורו אנו יכולים להשתמש באינטגרציית גאוס סטנדרטית:

שימוש בנוסחת Nanson עבור אינטגרציה משטחית. (Zohdi, 2018).

2. שימוש בנוסחת Nanson:

   לפיכך,

   כאשר הוא אלמנט השטח הדיפרנציאלי על האלמנט המסטר.

3. זיהוי הנורמל בנקודת גאוס על המשטח, והבטחה שאחת מקואורדינטות ה- מוגדרת כ-.

חישוב עיבורים ומאמצים (Post-Processing)

ה- post-processing עבור המאמץ, העיבור והאנרגיה מפתרון התזוזה הקיים, כלומר הערכים של התזוזות הצמתיות ופונקציות הצורה, הוא פשוט יחסית. בעיקרון התהליך זהה לזה של יצירת המערכת שיש לפתור. עבור כל אלמנט:

כאשר , , ו- הם הערכים בצומת עבור רכיבי , , ו-, וכאשר הקואורדינטות הגלובליות חייבות להיות מומרות למערכת המסטר, הן בטנזור הדפורמציה והן בייצוג התזוזה.

באופן טיפוסי, בתוך כל אלמנט, בכל נקודת גאוס, אנו מחברים את כל שמונה התרומות (מפונקציות הבסיס) עבור כל אחד מששת הרכיבים ולאחר מכן מכפילים בתזוזות הצמתיות המתאימות שחושבו קודם לכן. מיקומי נקודות גאוס הם המיקום המועדף ל- post-processing של הפתרון מכיוון שהם מציגים בדרך כלל מה שנקרא תכונות “super convergent” (מדויקות יותר מההערכות התיאורטיות). במילים אחרות, הם בדרך כלל המיקומים המדויקים ביותר של הקירוב של האלמנטים הסופיים.

הביטויים הבאים חייבים להיות מוערכים בנקודות גאוס, מוכפלים במשקלים המתאימים ומחוברים יחד:

כאשר מייצג את רכיב של התזוזה של הצומת ה-. על ידי שילוב הנגזרות הנומריות ליצירת העיבורים אנו מקבלים:

הערות שוליים

1. הצגת הקירוב הנומרי בצורה זו נועדה להקל על הבנת התהליך. ברמת המימוש, לא היינו מאחסנים את המטריצות בצורה זו בשל המספר הגדול של אפסים. ↩

2. זה לצורכי המחשה בלבד. לצורכי יעילות חישובית, לא צריך לתכנת פעולות כאלה בדרך זו. ברור שיש להימנע מכפל מיותר של אפסים. ↩

→ קודם: FEM1_005הבא: FEM1_007 ←