FEM1_001 מבוא ומידול בעיה חד ממדית

שיטות נומריות בסיסיות

בתרגול הראשון עוברים על:

1. טור טיילור
2. אינטרפולציה
3. אינטגרציה נומרית.

מ(Zohdi, 2018):

מבוא: שיטות שאריות המשוקללות

נביט במד”ר חד ממדית מהצורה

כאשר, למשל:

נשער פתרון מהצורה

כאשר ה--ים הם פונקציות קירוב, וה--ים הם קבועים לא ידועים שאנו צריכים למצוא. כאשר נחסר את הקירוב מהפתרון האמיתי, נישאר עם “שארית”:

אם אנו מניחים שאנו יודעים את ה--ים, נרצה לבחור את ה--ים כך שהשארית תהיה כמה שיותר קטנה. למעשה, אנו רוצים שה-נורמה של השארית, , תהיה כמה שיותר קטנה. אנו נחליט לעבוד עם נורמה-, המוגדרת:

כאשר ניקח את הנגזרת ביחס לכל , ונאפס, נקבל לכל :

זה מוביל אותנו ל- משוואות עם נעלמים. שיטה זו נקראת שיטת הריבועים הפחותים.

שיטת גלרקין

מתוך כל שיטות השארית המשוקללת, שיטת גלרקין (Galerkin’s method) היא הכי נפוצה ומדויקת למספר רב של בעיות.
נביט בפתרון האמיתי, המקורב, והשגיאה, הקשורים דרך:

כעזר, נתייחס להם כוקטורים:

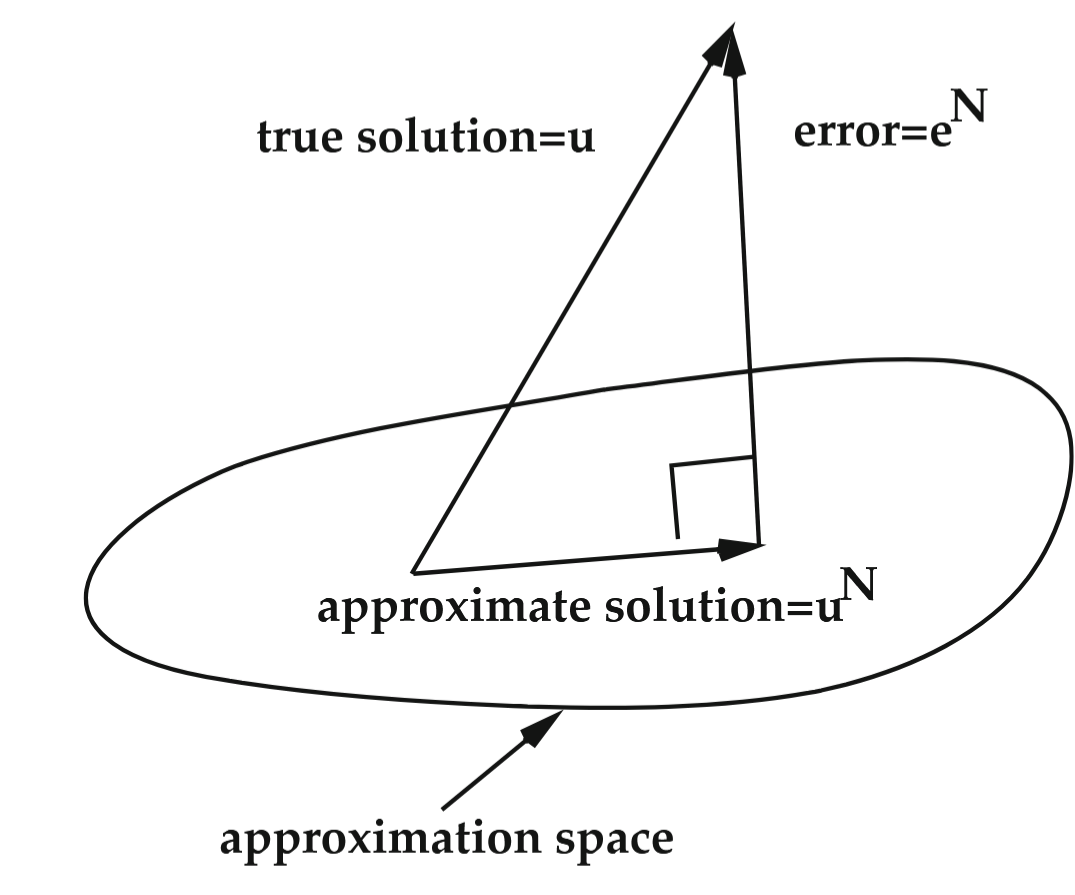
אורתוגונליות של שגיאת הקירוב. (Zohdi, 2018).

ניתן לראות שהשגיאה היא הקטנה ביותר כאשר היא אורתוגונלית ל-. הבעיה היא שהשגיאה לא ידועה. אבל, השארית, כן ידועה.

הערה:

בעוד השגיאה והשארית הם לא אותו הדבר, נשים לב שכאשר השארית אפס, השגיאה היא גם אפס.

הבחנה זו היא הבסיס לרעיון מאחורי שיטת גלרקין - נאלץ את השארית להיות אורתוגונלית . מתמטית, לפי ההגדרה של אורתוגונליות לפונקציות:

מכך אנו מקבלים משוואה אחת. לכן, אנו אוכפים זאת לכל אחד מהפונקציות קירוב, שביחד מרכיבים את מרחב הקירובים שבונים את ,

כעת יש לנו משוואות עם נעלמים, שאיתם נוכל לחשב את .

באופן יותר כללי, אם הבעיה מוגדרת על תחום ויש לה תנאי שפה נוימן על שפה , אז השיטה היא:

במקרה החד-ממדי כיוון שתנאי השפה הוא פשוט נקודה, אז:

השיטה הכללית:

1. חישוב השארית:
2. נאלץ את השארית להיות אורתוגונלית לכל אחת מהפונקציות קירוב:
3. נפתור את מערכת המשוואות (שהן כנראה מצומדות). המשוואה תהיה לינארית אם המשוואה הדיפרנציאלית לינארית, ואי-לינארית אם המשוואה הדיפרנציאלית אי-לינארית.

הבעיה המרכזית בשיטה זו היא שאין דרך שיטתית לבחירת פונקציות הקירוב . שיטת האלמנטים הסופיים הבסיסית פותחה כהרחבה לשיטת גלרקין ע”י בניית פונקציות כדי לטפל בבעיות כאלו. היא:

1. מבוססת על שיטת גלרקין.
2. שיטתי ויעיל מבחינה חישובית.
3. מבוססת על הגדרה מחדש של המד”ח כדי להימנע מהדרישות המחמירות של אופן פתירת המד”ח.

תרגילים

שאלה 1

נתונה הבעיה הבאה:

פתרונה האנליטי הוא:

פתרו אותה בשיטת גלרקין.

פתרון:
ראשית, נצטרך לבחור את פונקציות הבסיס לקירוב. נראה לי פולינומי לגראנז’ זה סבבה:

כאשר בביטוי השמאלי יש שימוש בעיקרון הסכימה של איינשטיין.
בבעיה זו יש לנו שני תנאי שפה מסוג דיריכלה, שאנו רוצים לקיים במדויק לפני שאנו פותרים את משוואה זו (לפונקציות שמקיימות זאת אנו קוראים פונקציות קבילות קינמטית). זה אומר שמספר הנקודות המינימלי שאנו צריכים כדי לבנות את הפולינומים הוא . במקרה זה ישנם נעלמים שנחשבם לפי התנאי שפה ואחד לפי המשוואה עצמה. נבחר את הנקודות:

כאשר את בחרנו שרירותית. לכן, הפולינומים יהיו:

נדרוש מתנאי השפה ש:

הערה:

היה אפשר גם לראות זאת ישירות מעצם הגדרת פולינומי לגראנז’.

כעת נוכל להגדיר את השארית:

נשים לב ש-, האופרטור הלינארי, במקרה שלנו הוא:

ולכן השארית:

כאשר שוב, השתמשנו כאן בעיקרון הסכימה של איינשטיין.
נפעיל כעת את שיטת גלרקין:

נסדר מחדש את הביטוי:

משוואה (למעשה שלוש משוואות) היא מערכת משוואות לינאריות שניתן לרשום בצורה:

השורה הראשונה והשלישית במטריצה והוקטור הם למעשה תנאי השפה:

כאשר:

כדי לפשט את אנו יכולים להזיז את העמודה הראשונה והשלישית של המטריצה לצד ימין כדלהלן (וואו בחיים שלי לא השתמשתי במילה הזאת):

כעת נוכל לפשט את מערכת המשוואות ולפתור רק מטריצה :

כעת, נצטרך לפתור את האינטגרלים. נוכל לעשות זאת בעזרת אינטגרציית גאוס. מאחר ופונקציות הבסיס הם פולינומים מסדר , השגיאה תהיה . כדי לעשות זאת נצטרך נקודות גאוס. אנו גם נצטרך להמיר לאינטגרציה על התחום :

במקרה שלנו ו- . הנקודות הן , והמשקלים . נקבל כי:

נציב ב-:

לבסוף, לאחר שאנו יודעים את כל הערכים של הפתרון בצמתים, אנו יכולים לבצע אינטרפולציה ולקבל את הפתרון המקורב:

הפתרון באיורים הבאים התקבל מאינטגרציית גאוס בשלוש נקודות.

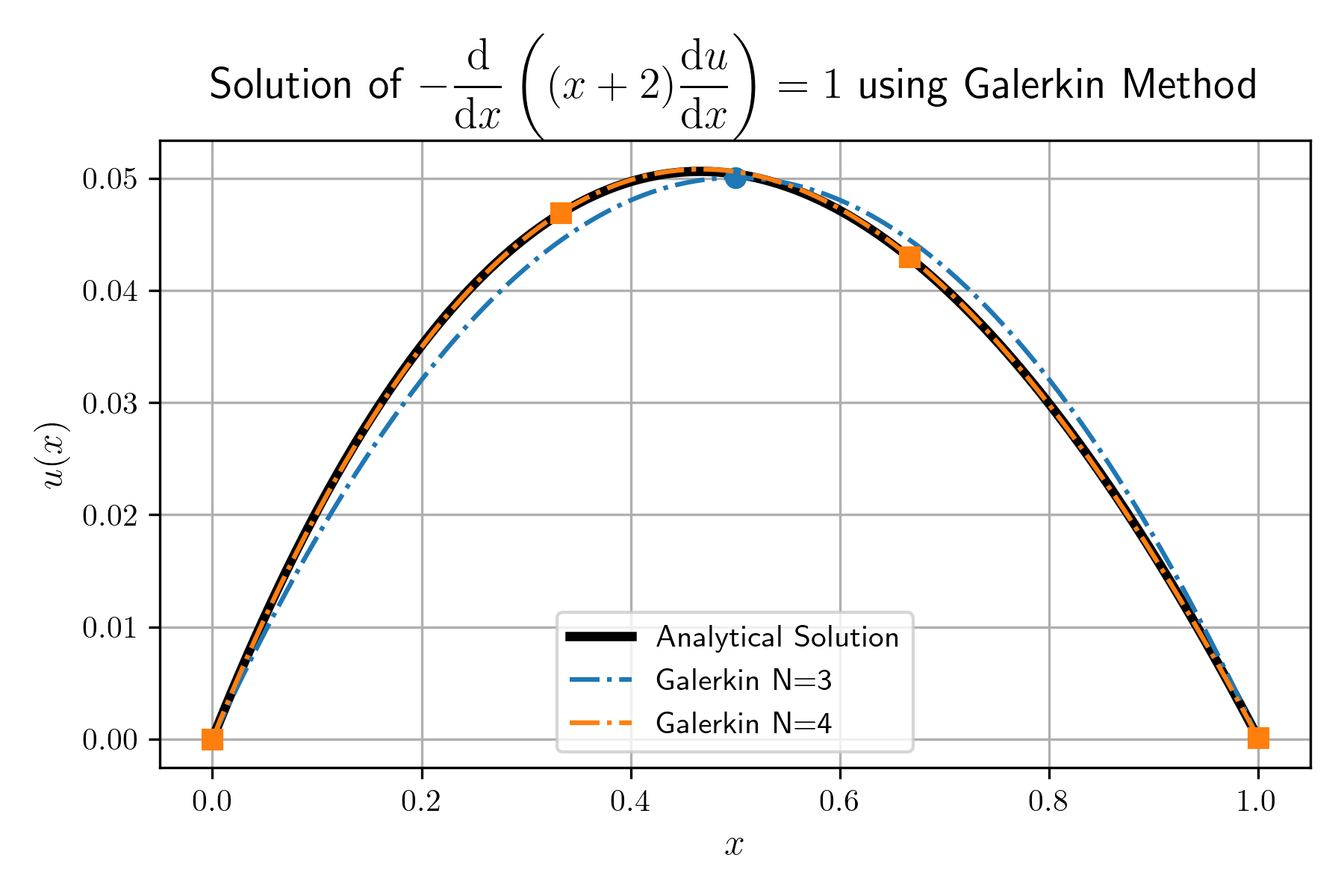
פתרון אנליטי ונומרי לבעיה.

בקירוב ממעלה גבוהה () (אבל עדיין עם אינטגרציית גאוס בשלוש נקודות) אנו נקבל קירוב פחות טוב. הסיבה היא שלאינטגרציה בשלוש נקודות יש שגיאת קיטוע מסדר , האינטגרנד הוא פולינום ממעלה תשיעית, ואורך הקטע הוא . במקרה זה פעולת האינטגרציה מוסיפה שגיאה משמעותית לפתרון. כדי לקבל פתרון מדויק, עלינו להשתמש ביותר נקודות אינטגרציה, או לחלק כל קטע למספר תת-קטעים לאינטגרציה.