פנגייה

FEM1_008 משוואת האלסטיות הדו-ממדית

• זמן קריאה: 22 דק'

צורה חלשה של משוואת האלסטיות

בקירוב אלמנטים סופיים ראינו כבר שהצורה החלשה של משוואת האלסטיות היא:

מיפוי אלמנט משולש לינארי כללי

בדיוק כמו במיפוי אלמנט משולש בבעיית פואסון, מטריצת הקשיחות האלמנטרית תהיה מהצורה:

כאשר האנלוגיות הן במקום ו- במקום .

אלמנט המסטר ופונקציות הצורה

גם כאן נבחר אלמנט מסטר משולש במערכת קואורדינטות מקומית . קונפיגורציה נפוצה היא משולש ישר זווית עם צמתים בנקודות:

  • צומת מקומי 1:
  • צומת מקומי 2:
  • צומת מקומי 3:

אלמנט מסטר למשולש.

פונקציות הצורה הלינאריות על אלמנט המסטר, המסומנות כ- , הן:

לכל פונקציית צורה יש ערך בצומת המקומי ו- בשני הצמתים האחרים. שטח אלמנט המסטר הוא .

מיפוי איזופרמטרי מאלמנט המסטר לאלמנט הפיזיקלי

אלמנט משולש פיזיקלי במרחב הגלובלי מוגדר על ידי קואורדינטות צמתיו: , , ו-. אנו מניחים שהצומת הגלובלי מתאים לצומת המקומי .

המיפוי (טרנספורמציה) מקואורדינטות מקומיות לקואורדינטות גלובליות ניתן על ידי:

טרנספורמציה של נגזרות ומטריצת היעקוביאן

בדיוק כמו בבעיית פואסון, במקרה של משולש:

כאשר נוכל לרשום את הטרנספורמציה של הנגזרות באופן מטריצי:

ו- מכילה את הנגזרות הגלובליות של כל פונקציות הצורה:

מטריצת הדפורמציה ומטריצת פונקציות הצורה

באלסטיות דו-ממדית, אנו זקוקים לחישוב עבור מטריצת הקשיחות. תחילה נגדיר את מטריצת פונקציות הצורה ואת מטריצת הדפורמציה .

מטריצת פונקציות הצורה :
עבור אלמנט משולש עם שלושה צמתים, כל צומת בעל שתי דרגות חופש (תזוזה ב- ותזוזה ב-), עם סידור התזוזות , מטריצת פונקציות הצורה היא:

וקטור התזוזות הצומתיות הוא:

כך שהתזוזות בתוך האלמנט ניתנות על ידי:

מטריצת הדפורמציה :
עבור מצב מישור מאמץ (plane stress) או מישור עיבור (plane strain), וקטור העיבורים מכיל שלושה רכיבים:

מטריצת הדפורמציה היא האופרטור הדיפרנציאלי:

חישוב :
כאשר נפעיל את מטריצת הדפורמציה על מטריצת פונקציות הצורה עם הסידור החדש, נקבל:

התוצאה זהה למקרה הקודם מכיוון שסידור הרכיבים במטריצת פונקציות הצורה נשאר עקבי עם סידור וקטור התזוזות.

מטריצות האלמנט המסטר

נוכל לרשום את מטריצת הקשיחות האלמנטרית באופן הבא:

כאשר את ו- אנו מגדירים באופן הבא:
מטריצת הדפורמציה באלמנט המסטר :
עבור בעיות דו-ממדיות באלמנט המסטר:

מטריצת פונקציות הצורה באלמנט המסטר :

עבור אלמנט משולש עם שלושה צמתים ושתי דרגות חופש לכל צומת:

חישוב :
הנגזרות של פונקציות הצורה הלינאריות:

כאשר נפעיל את מטריצת הדפורמציה על מטריצת פונקציות הצורה:

במקרה של אלמנט משולש:

זוהי המטריצה הקבועה שתשמש בחישוב מטריצת הקשיחות האלמנטרית. המטריצה מקשרת בין וקטור התזוזות הצומתיות לוקטור העיבורים באלמנט המסטר.

מטריצת הקשיחות עבור מישור מאמץ ומישור עיבור

עבור חומר איזוטרופי, מטריצת הקשיחות שונה בין מצב מאמצים מישורי למצב עיבורים מישורי:

מצב מאמצים מישורי (Plane Stress):

מצב עיבורים מישורי (Plane Strain):

כאשר הוא מודול האלסטיות ו- הוא מקדם פואסון.

אינטגרציה נומרית - אינטגרציית גאוס עבור משולשים

עבור חישוב מטריצת הקשיחות האלמנטרית באמצעות אינטגרציית גאוס:

כאשר הם משקלי הגאוס ו- הוא מספר נקודות הגאוס.
במידה ו- הוא עובי האלמנט והוא קבוע, החישוב יהיה:

נזכור שלפי גזירה בקואורדינטות הייחוס, את וקטור העומסים נחשב לפי:

אם הוא עובי קבוע:

חישוב עיבורים ומאמצים (Post-Processing)

לאחר פתרון מערכת המשוואות ומציאת התזוזות הצמתיות, יש לחשב את העיבורים והמאמצים בכל אלמנט.

עבור כל אלמנט, לאחר שמצאנו את וקטור התזוזות הצמתיות , ניתן לחשב את העיבורים והמאמצים באופן הבא:

חישוב העיבורים:
השיטה היעילה ביותר לחישוב עיבורים היא לנצל את החישובים שכבר בוצעו עבור מטריצת הקשיחות:

שלב 1: שימוש ביעקוביאן ההפוך שכבר חושב
במקום לחשב מחדש את הנגזרות הפיזיקליות, נשתמש במטריצת היעקוביאן ההפוכה שכבר חושבה:

כאשר היא מטריצת הנגזרות במערכת המסטר:

שלב 2: יצירת מטריצת עיבור-תזוזה פיזיקלית

כאשר הנגזרות הפיזיקליות מתקבלות מ-:

שלב 3: חישוב העיבורים הפיזיקליים

חישוב המאמצים:
המאמצים מחושבים באמצעות חוק הוק:

עבור מצב מאמצים מישורי:

מיקום החישוב - נקודות גאוס:
כפי שמתואר בpost-processing, העיבורים והמאמצים מחושבים בדרך כלל בנקודות גאוס מכיוון שהן מציגות תכונות super convergent - כלומר, הן המיקומים המדויקים ביותר של הקירוב של האלמנטים הסופיים.

עבור אלמנטים משולשיים לינאריים, נקודת גאוס אחת במרכז המשולש () מספיקה לחישוב מדויק.

מאמץ פון מיזס משמש להערכת כניעה בחומרים דקטיליים.
התהליך הנומרי כולל:

  1. עבור כל אלמנט: מיצוי התזוזות הצמתיות מהפתרון הגלובלי
  2. חישוב מטריצת העיבור-תזוזה: בנקודות גאוס
  3. חישוב העיבורים:
  4. חישוב המאמצים:
  5. חישוב גדלים נוספים: מאמצים עיקריים, מאמץ פון מיזס, זוויות

תרגילים

שאלה 1

סכמת הבעיה.

נתונה הבעיה הבאה:

בנוסף, נתון כי:

פתרו את הבעיה עם שני אלמנטים משולשיים (מצב מאמצים מישורי).

רישות התחום.

פתרון:

שלב 1: הגדרת הרשת:
בהתאם לאיור, נחלק את התחום לשני אלמנטים משולשיים:

  • אלמנט 1: צמתים
  • אלמנט 2: צמתים

קואורדינטות הצמתים:

שלב 2: תנאי שפה ועומסים:
תנאי שפה קבועים (צומת ו-):

עומסים חיצוניים על הצד הימני ():
העומס פועל על הצד בין צמתים ו-.
אורך הצד: .
כוח כולל: .

העומס מתחלק שווה בין שני הצמתים:

שלב 3: מטריצת הקשיחות החומר:
עבור מצב מאמצים מישורי:

נציב ערכים:

שלב 4: חישוב מטריצות קשיחות אלמנטריות:
אלמנט (צמתים ):
קואורדינטות: , ,
מטריצת היעקוביאן:

אלמנט (צמתים ):
קואורדינטות: , ,
מטריצת היעקוביאן:

שלב 5: חישוב מטריצות הקשיחות האלמנטריות באמצעות אינטגרציית גאוס:
מטריצת הקשיחות האלמנטרית מחושבת לפי:

כאשר הוא מספר נקודות הגאוס, הם משקלי הגאוס, ו- הוא עובי האלמנט.

עבור אלמנטים משולשיים לינאריים, מטריצות , , ו- הן קבועות על פני האלמנט. לכן:

עבור משולש מסטר, .
לכן:

כאשר הוא:

חישוב המטריצה:
עבור שני האלמנטים (מכיוון שיש להם אותו ), נקבל:

מכיוון ששני האלמנטים שלנו הם משולשים זהים מבחינת גודל וצורה (עם לשניהם), שניהם ייתנו את אותה מטריצת קשיחות:

הערה:

השימוש באינטגרציית גאוס עם נותן תוצאה מדויקת עבור אלמנטים לינאריים מכיוון שהאינטגרנד קבוע על פני כל אלמנט מסטר.

שלב 6: הרכבת המטריצה הגלובלית:
מטריצת הקשיחות הגלובלית מגודל ( צמתים × דרגות חופש):

וקטור התזוזות הגלובלי:

מיפוי צמתים לאלמנטים:

  • אלמנט 1: צמתים :
  • אלמנט 2: צמתים :

המטריצה הגלובלית לאחר הרכבה:

שלב 7: חישוב וקטור הכוחות האלמנטרי:
לפי שיטת האלמנטים הסופיים התלת-ממדית, וקטור הכוחות האלמנטרי מחושב באמצעות:

כאשר:

  • הביטוי הראשון מייצג תרומת כוחות הגוף (body forces)
  • הביטוי השני מייצג תרומת כוחות המשטח (traction forces)
  • הוא היעקוביאן המשטחי של קצה האלמנט

חישוב תרומת כוחות הגוף:
במקרה שלנו, , לכן התרומה הראשונה היא אפס עבור כל האלמנטים.

חישוב תרומת כוחות המשטח:
העומס פועל על הצד הימני () בין צמתים ו-.

עבור אלמנט (צמתים ), הצלע נמצאת על השפה :

  • נקודות הגאוס על הצלע: אנו משתמשים באינטגרציית גאוס חד-ממדית על הצלע
  • היעקוביאן המשטחי: כאשר הוא אורך הצלע

עבור הצלע בין צמתים ו-:

  • אורך הצלע:
  • היעקוביאן:

וקטור הכוחות במערכת מקומית עבור הצלע ():

עבור אינטגרציית גאוס חד-ממדית עם נקודה אחת ():

פונקציות הצורה על הצלע במרכז הצלע ():

  • צומת :
  • צומת :

לכן:

נציב:

וקטור הכוחות הגלובלי:
לאחר הרכבה גלובלית עם המיפוי :

שלב 8: יישום תנאי השפה:
תנאי השפה:
עם הסידור החדש: DOFs מקובעים.
נמחק את שורות ועמודות .

המטריצה המוקטנת (עבור ):

וקטור הכוחות (עבור ):

שלב 9: פתרון המערכת:

פתרון המערכת נותן:

פתרון סופי:

שלב 10: חישוב עיבורים ומאמצים (Post-Processing)

לאחר מציאת התזוזות, נחשב את העיבורים והמאמצים בכל אלמנט בנקודות גאוס, בהתאם לתיאוריה שפותחה למעלה.

אלמנט 1 (צמתים 1-2-3):
התזוזות הצמתיות:

בנקודת גאוס ():
עיבורים:

מאמצים:

אלמנט 2 (צמתים 3-4-1):
התזוזות הצמתיות:

בנקודת גאוס ():

עיבורים:

מאמצים:

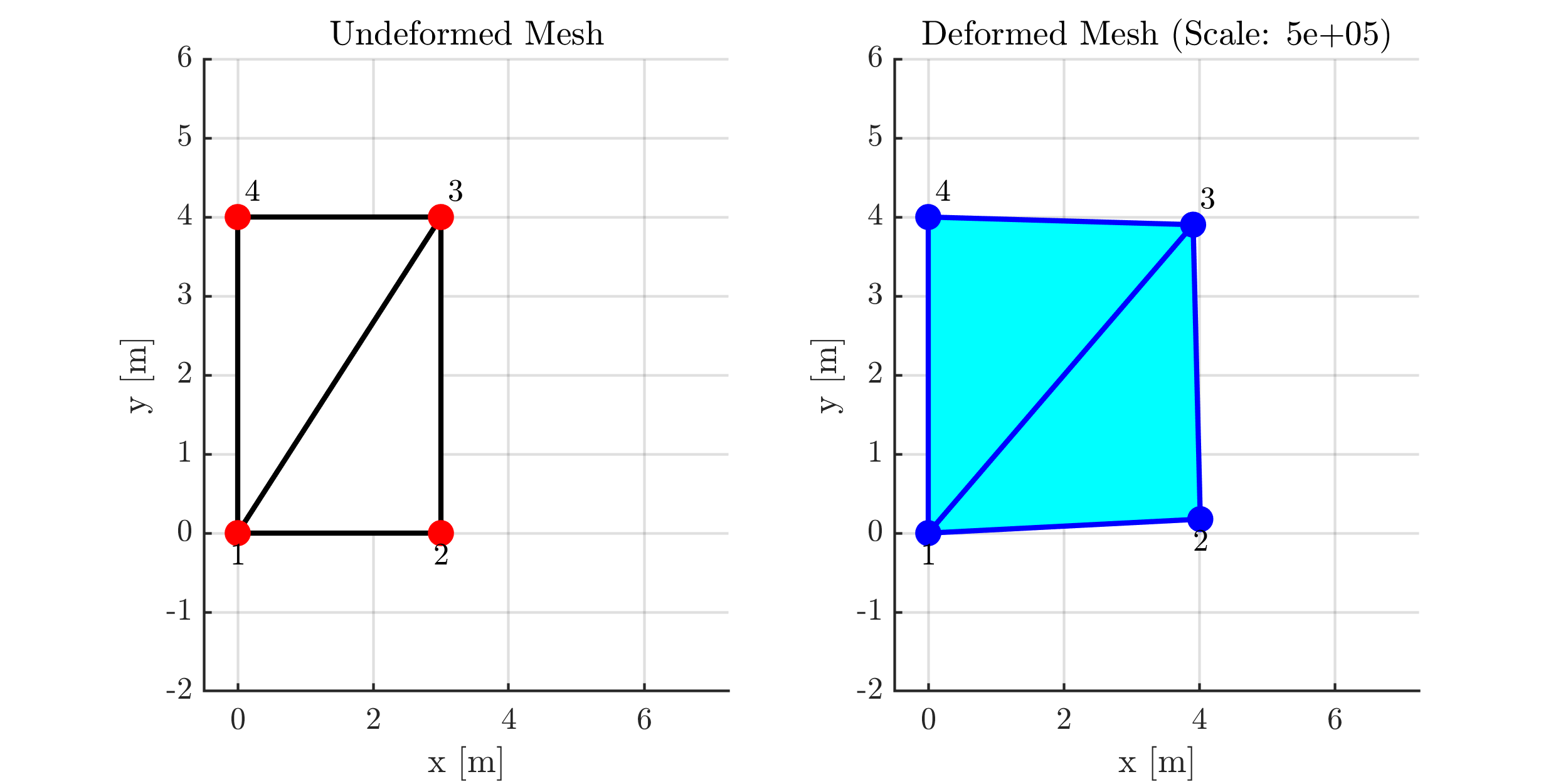
bookhue

הגזמה של התזוזות לבעיה הנתונה.

שאלה 2

נתונה הבעיה משאלה קודמת עם שינוי קטן:

סכמת הבעיה.

פתרו את הבעיה עם שלושה אלמנטים משולשיים (מצב מאמצים מישורי):

רישות התחום.

פתרון:

שלב 1: הגדרת הרשת:
בהתאם לאיור, נחלק את התחום לשלושה אלמנטים משולשיים:

  • אלמנט 1: צמתים
  • אלמנט 2: צמתים
  • אלמנט 3: צמתים

קואורדינטות הצמתים:

שלב 2: תנאי שפה ועומסים:
תנאי שפה קבועים (צומת ו-):

עומסים חיצוניים על הצד הימני המשופע:
העומס פועל כהתפלגות משולשית על צלע :

  • בצומת : עומס =
  • בצומת : עומס =

חישוב אורך הצלע והכיוון:
אורך צלע :

וקטור הצלע:
וקטור הנורמל (החוצה): (כיוון דרום-מזרח כללי)

כוחות צמתיים שקולים להתפלגות משולשית:
עבור התפלגות משולשית מ- ל- על אורך :

  • בצומת הקטן ():
  • בצומת הגדול ():

רכיבי הכוחות:

שלב 3: מטריצת הקשיחות החומר:
עבור מצב מאמצים מישורי:

נציב ערכים:

שלב 4: חישוב מטריצות קשיחות אלמנטריות:

אלמנט (צמתים ):
קואורדינטות: , ,

אלמנט (צמתים ):
קואורדינטות: , ,

אלמנט (צמתים ):
קואורדינטות: , ,

שלב 5: מטריצות הקשיחות האלמנטריות:
לכל שלושת האלמנטים , לכן:

עם הממד , נקבל מטריצות קשיחות דומות לשאלה 1 אך עם ערכים מותאמים.

שלב 6: הרכבת המטריצה הגלובלית:
מטריצת הקשיחות הגלובלית בגודל ( צמתים × דרגות חופש).

וקטור התזוזות הגלובלי:

המטריצה הגלובלית לאחר הרכבה:

שלב 7: וקטור הכוחות הגלובלי:
העומסים פועלים על צמתים ו- בהתאם להתפלגות המשולשית:

שלב 8: יישום תנאי השפה:
תנאי השפה הם: .
נישאר עם DOFs:

שלב 9: פתרון המערכת:
לאחר פתרון המערכת המוקטנת באמצעות MATLAB, נקבל את התזוזות הצמתיות.

פתרון סופי:

שלב 10: חישוב עיבורים ומאמצים (Post-Processing)
לאחר מציאת התזוזות, נחשב את העיבורים והמאמצים בכל אלמנט בנקודות גאוס, בהתאם לתיאוריה שפותחה למעלה.

אלמנט 1 (צמתים 1-2-3):
התזוזות הצמתיות:

בנקודת גאוס ():
עיבורים:

מאמצים:

אלמנט 2 (צמתים 3-4-1):
התזוזות הצמתיות:

בנקודת גאוס ():

עיבורים:

מאמצים:

אלמנט 3 (צמתים 2-5-3):
התזוזות הצמתיות:

בנקודת גאוס ():

עיבורים:

מאמצים:

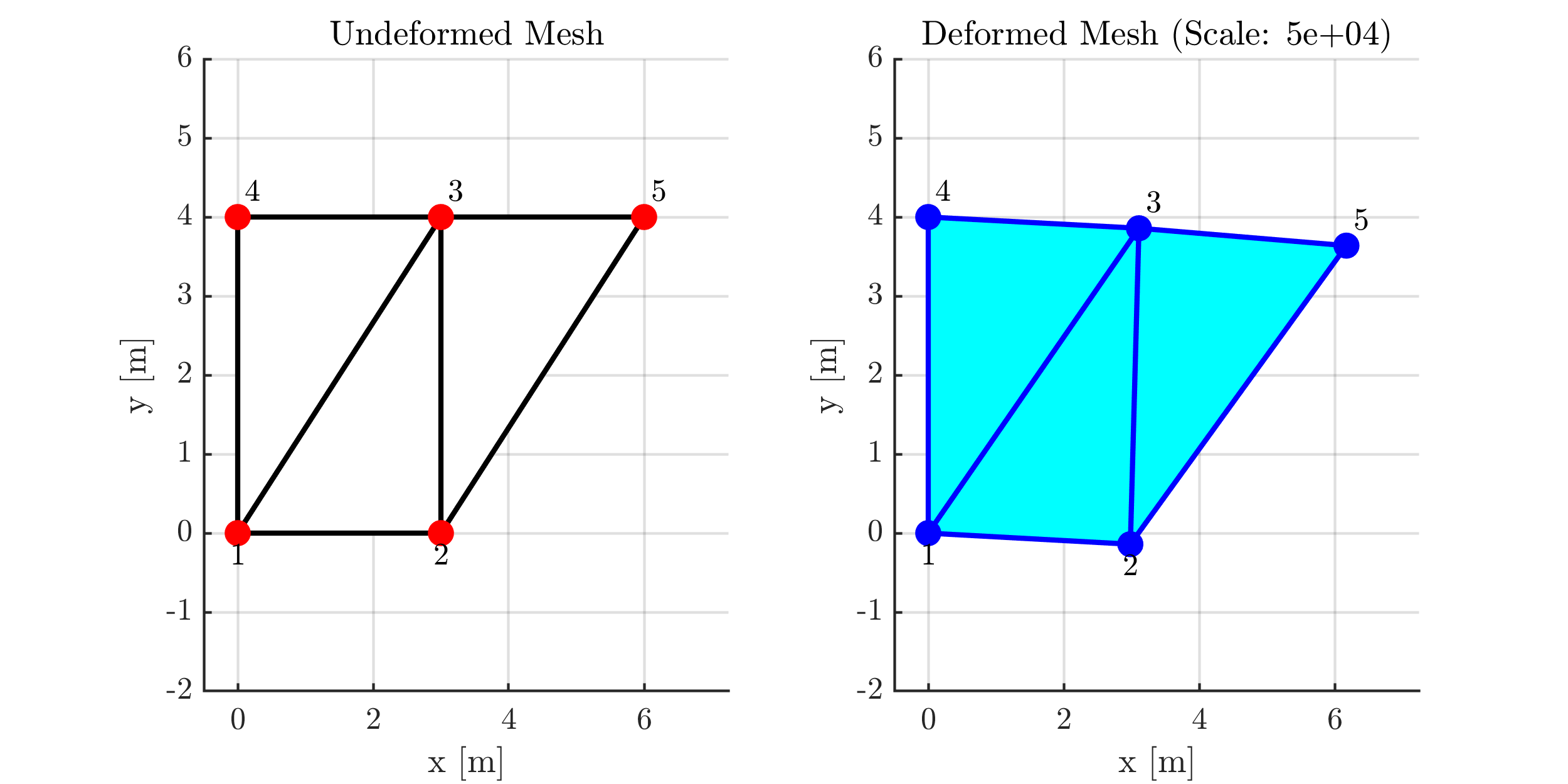
bookhue

הגזמה של התזוזות לבעיה הנתונה.

עמודים המציינים את העמוד הזה