שאלה 1
נתון:
סעיף א’
באותו אופן כמו בהרצאה, נתחיל מאינטגרציה על התחום:
נכפול בפונקציית בוחן קבילה קינמטית
נבצע אינטגרציה בחלקים על הביטוי השני באגף ימין:
נבצע עוד אינטגרציה בחלקים על הביטוי השלישי באגף ימין:
מאחר ויש לנו תנאי שפה דיריכלה ב-
נציב את תנאי השפה שיש לנו על
נעדיף חלק מהביטויים באגף שמאל:
סעיף ב’
עבור אלמנט אחד,
נבצע את הקירובים הבאים:
כך שנוכל לרשום את (E1.1) גם כ:
בצורה מטריצית:
כאשר:
נחשב כעת כל אחד מביטויים אלו במפורש. אנו משתמשים בפונקציות הבסיס כפי שמצוין במשוואה (OA5.60):
הנגזרות שלהן:
הערה:
אלו הן פונקציות בסיס בתחום
, כי משום מה זה התחום שהספר בחר. זה לא כזה משנה כי בכל מקרה המטריצות שמחושבות מפונקציות בסיס אלו מחושבות במדויק, כך שאנו מקבלים תוצאות זהות.
בעזרת משוואה (10.2), משוואה (E1.2) היא:
בעזרת משוואה (OA5.82), משוואה (E1.3) היא:
משוואה (E1.4) תהיה (בעזרת משוואה (10.2)):
נזכור כי יש לנו תנאי שפה דיריכלה הומוגניים ב-
סעיף ג’
הלו הלו מה אנחנו ברטט??? לא בחומר בעלילללללל.
סעיף ד’
גם כן לא בחומרררר (אולי רק החלק הסטטי).
סעיף ה’
חלק מהאיברים (האיברים הקשורים לאינרציית הזרוע) במטריצת המסה ווקטור העומס פשוט ייעלמו:
שאלה 2
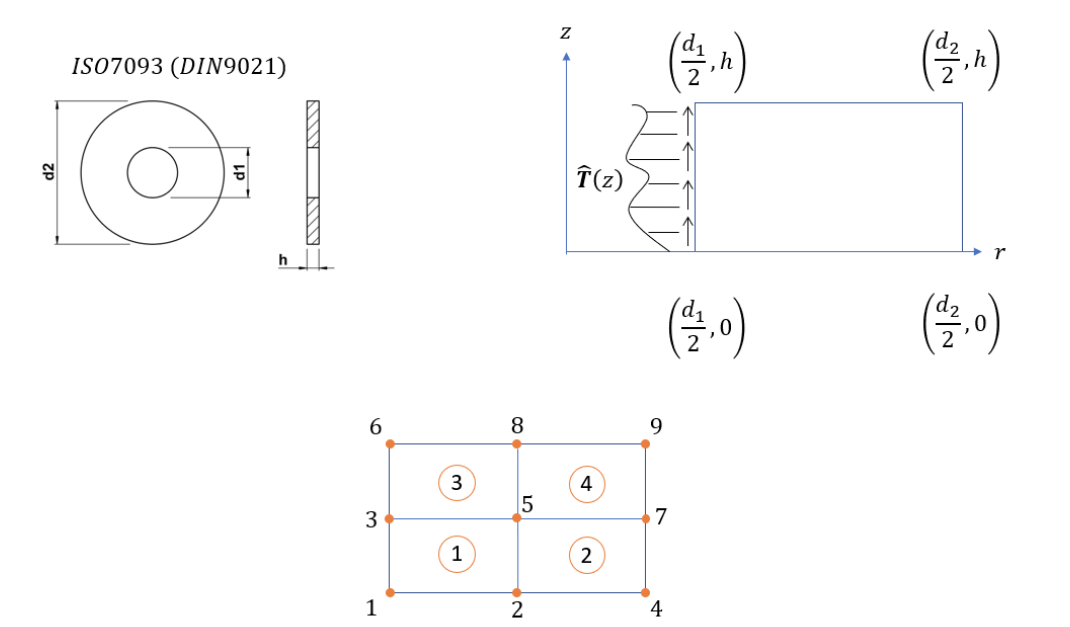
איור E2020.1: הבעיה הנתונה.
סעיף א’
לא באמת עברנו בקורס על מערכות אקסיסימטריות, אז אנחנו לא ממש אמורים להבין מה קורה פה.
סעיף ב’
לפי הרישות הנתון:
מיקום כל הצמתים:
תנאי שפה דיריכלה:
תנאי שפה נוימן:
סעיף ג’
אלמנט
נבחר באינטגרציית גאוס בנקודה
לפי מיפוי עבור משוואת האלסטיות:
לפי אינטגרציית גאוס בנקודה אחת עבור אלמנט מרובע,
סעיף ד’
די חלאס.
שאלה 3
סעיף א’
עבור אלמנט טטרהדר נבחר בצמתים:
נבסס את הפונקציות על פי פולינום לינארי, כלומר:
באופן מאוד דומה למקרה של משולש, ניתן להראות ש:
סעיף ב’
בעזרת אינטרפולציה (לינארית או קוודרטית או אפילו מסדר יותר גבוה, כתלות באלמנט שנבחר) בין הצמתים.
סעיף ג’
פתרון רשמי:
הביטוי
סעיף ד’
פתרון רשמי:
כאשר נמקם את צמתי האלמנט במרחב עלינו להקפיד על שתי נקודות:
- מיקום הצמתים לא ייצור טרנספורמציה בלתי הפיכה בין התחום הגלובלי ללוקלי )כלומר יעקוביאן הטרנספורמציה לא מתאפס(. אי הקפדה על נקודה זו תייצר אלמנט לא פתיר
- צורת האלמנט לא תיצור מטריצת קשיחות Ill-Conditioned – בדרך כלל בבעיות רב ממדיות מצביע על אלמנטים שיחס ממדיהם אינו בסדר גודל זהה (“אלמנטי סיכה”( . אי -הקפדה על נק’ זו תיצור אלמנט בעל שגיאה נומרית גבוהה, שהתכנסותו איטית, ופתרונו קשה למחשב.
