מבוא
בפרק זה נציג את הנוהל לניתוח מבנה נושא עומסים. נתייחס למבנים המורכבים ממספר אלמנטים הקשורים זה לזה בנקודות צימוד. המבנה נתמך כראוי וחשוף לעומסים. הנעלמים הם העיוותים של המבנה וכוחות התגובה בתמיכות. בנוסף, התגובות הפנימיות של האלמנט הבודד הן בעלות עניין. יחסי הקשיחות של האלמנטים הבודדים כבר ידועים מהפרקים הקודמים. יחס קשיחות גלובלי נוצר על בסיס יחסי הקשיחות הבודדים הללו. מנקודת מבט מתמטית, הערכת יחס הקשיחות הגלובלי שווה לפתרון מערכת משוואות לינארית.
הרכבת יחס הקשיחות הגלובלי
הקמת יחס הקשיחות הגלובלי מתרחשת במספר שלבים:
- מטריצת הקשיחות הבודדת
- ידוע אילו צמתים מחוברים לכל אלמנט. לכן ניתן לנסח את יחס הקשיחות הבודד לכל אלמנט בקואורדינטות מקומיות:
$$
[\mathbf{K}^{e}]{ \mathbf{a} }=[\mathbf{R}^{e}]כ א ש ר א נ ו מ ק ר ב י ם א ת ל פ י - יחס הקשיחות הבודד, המנוסח בקואורדינטות מקומיות, חייב להיות מנוסח בקואורדינטות גלובליות.
- הממד של מטריצת הקשיחות הגלובלית מוגדר דרך סכום דרגות החופש הגלובליות בכל הצמתים.
- יש להגדיר מספור של הצמתים ושל דרגות החופש בכל צומת.
- הערכים ממטריצת הקשיחות הבודדת צריכים להיות ממוינים במיקומים המתאימים במטריצת הקשיחות הגלובלית.
ניתן להדגים זאת בעזרת דוגמה פשוטה. נתון מבנה דמוי מוט באורך
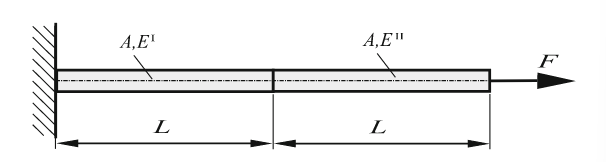
איור 9.1: מבנה דמוי מוט באורך
. (Öchsner & Merkel, 2018).
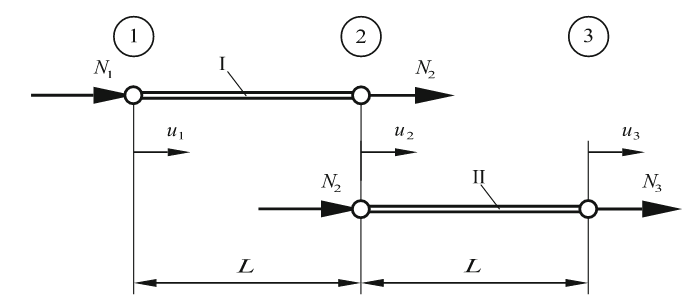
איור 9.2: מבנה בדיד עם שני אלמנטים סופיים. (Öchsner & Merkel, 2018).
הצמתים
כאשר:
הצמתים
כאשר:
מאחר שמערכות הקואורדינטות המקומיות והגלובליות זהות לבעיה הנוכחית, טרנספורמציית הקואורדינטות מושמטת. הממד של יחס הקשיחות הגלובלי
מבנה מישורי עם שני מוטות
כדוגמה ראשונה ופשוטה ידון במבנה העשוי משני מוטות. שני המוטות בעלי אותו אורך
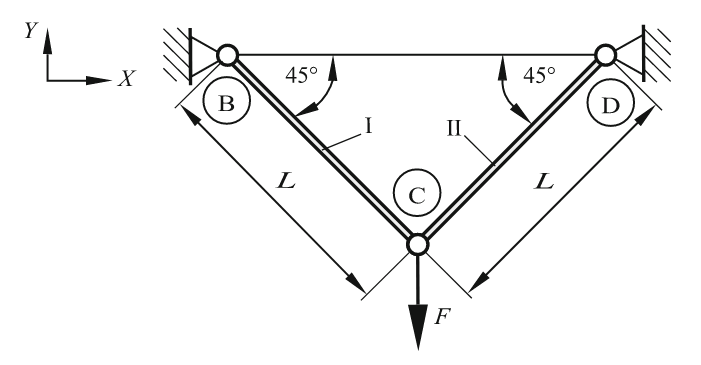
איור 9.3: מבנה מישורי העשוי משני מוטות. (Öchsner & Merkel, 2018).
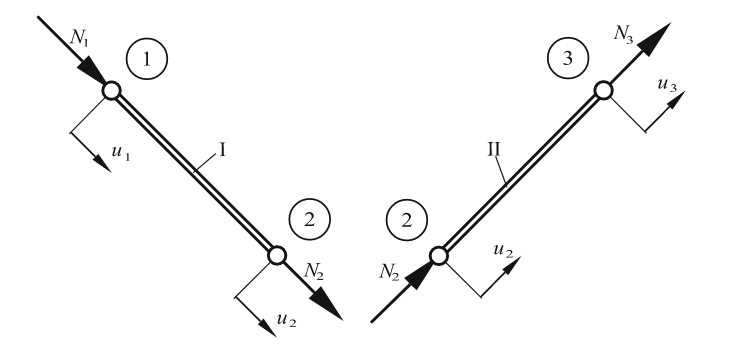
איור 9.4: מבנה מישורי עם שני אלמנטי מוט. (Öchsner & Merkel, 2018).
נתון:
לא ידועים:
- ההזזה במיקום
- המעוות והמאמץ באלמנטים
פתרון:
הדיסקרטיזציה הפשוטה ביותר של המבנה ברורה. המבנה מחולק לשני אלמנטים. הצמתים עם המספרים
כאשר:
הצמתים
כאשר:
אלמנט
לאלמנט
לאלמנט
ולאלמנט
מקבלים את יחס הקשיחות הגלובלי על ידי הכנסת יחסי הקשיחות הבודדים במיקומים המתאימים:
בשלב הבא, תנאי השפה יוכנסו:
- ההזזה בצומת
- הכוח החיצוני בצומת
בכך יחס הקשיחות הגלובלי הוא:
לאחר מחיקת השורות והעמודות
עם השורות והעמודות
מכאן ניתן לקבוע את ההזזות הלא ידועות
דרך טרנספורמציה של ההזזות
מההזזות המקומיות המעוות:
ניתן לקבוע. לאחר שההזזות המקומיות באלמנטים הפרטיים ידועות, הכוחות המקומיים ניתן לקבוע דרך יחס הקשיחות הבודד:
מוט
מוט
מההגדרה של כוח המוט מתברר שגם מוט
ובמוט
בכך גם תנאי העמסה באלמנטים הבודדים ידועים.
