מבוא
קורות הן אלמנטים מבניים שאורכם גדול מאוד בהשוואה לממדי החתך, הן נתמכות במספר נקודות לאורכם, ומועמס עליהן עומסים רוחביים לציר הקורה שגורמים לכיפוף. הקו הישר המחבר את כל המרכזי הגאומטריים של חתכי הקורה נקרא הציר המרכזי ולרוב נבחר אותו כציר
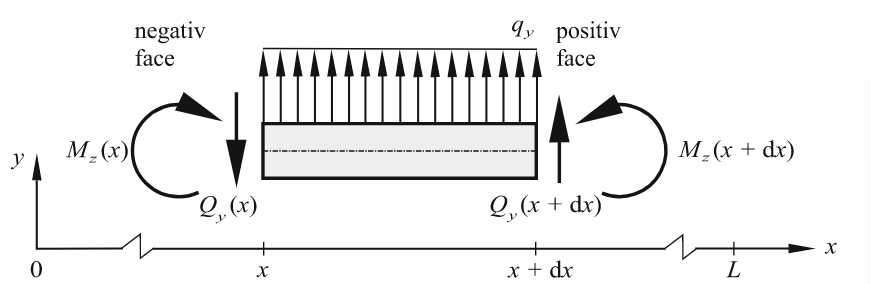
איור 10.1: אלמנט קורה איניפיניטסימלי עם תגובות פנימיות ועומסים במישור
. (Öchsner & Merkel, 2018).
הערה:
הסימון המקובל בקורס ובספר הוא
עבור כוח גזירה (לעומת ).
אלמנט קורת אוילר-ברנולי
המשוואה השולטת
תורת קורת אויילר-ברנולי (EBT) מבוססת על ההנחה שחתכים מישוריים המאונכים לציר הקורה נשארים מישוריים, קשיחים ומאונכים לציר לאחר הדפורמציה. תחת הנחות אלו, הראה במוצקים 2 שעבור קורה מישורית הנתונה לעומסים כמו באיור 10.1 (קורה בכיוון
במקרה של
כאשר
מבחינת הקשרים האחרים:
פיתוח הצורה החלשה
כדי לפתח את הצורה החלשה של משוואה (OA5.35), אנו כופלים אותה בפונקציית בוחן
נפרק את האינטגרל לשלושה חלקים:
נבצע אינטגרציה בחלקים על הביטוי הראשון:
נבצע אינטגרציה בחלקים נוספת על הביטוי השני בצד ימין של המשוואה:
נציב את משוואות (RJ5.13) ו-(RJ5.14) חזרה במשוואה (RJ5.12) ונקבל:
שיטת האלמנטים הסופיים עבור כפיפת קורות במישור
אלמנט הכיפוף מוגדר כגוף פריזמטי עם ציר ה-
איור 10.2: הגדרת הכיוון החיובי עבור אלמנט הכיפוף בדפורמציה במישור
.
מאחר שפרמטרי דפורמציה קיימים בשני הצמתים, כלומר
שדה הסיבוב מתקבל על ידי גזירה ביחס לקואורדינטת ה-
הערכה של התפלגויות הדפורמציה
צומת 1:
צומת 2:
ובסימון מטריצי:
פתרון עבור המקדמים הלא ידועים
או בסימון מטריצי:
מטריצת השורה של פונקציות הצורה נובעת מ-
ייצוג גרפי של פונקציות הצורה מוצג באיור הבא:
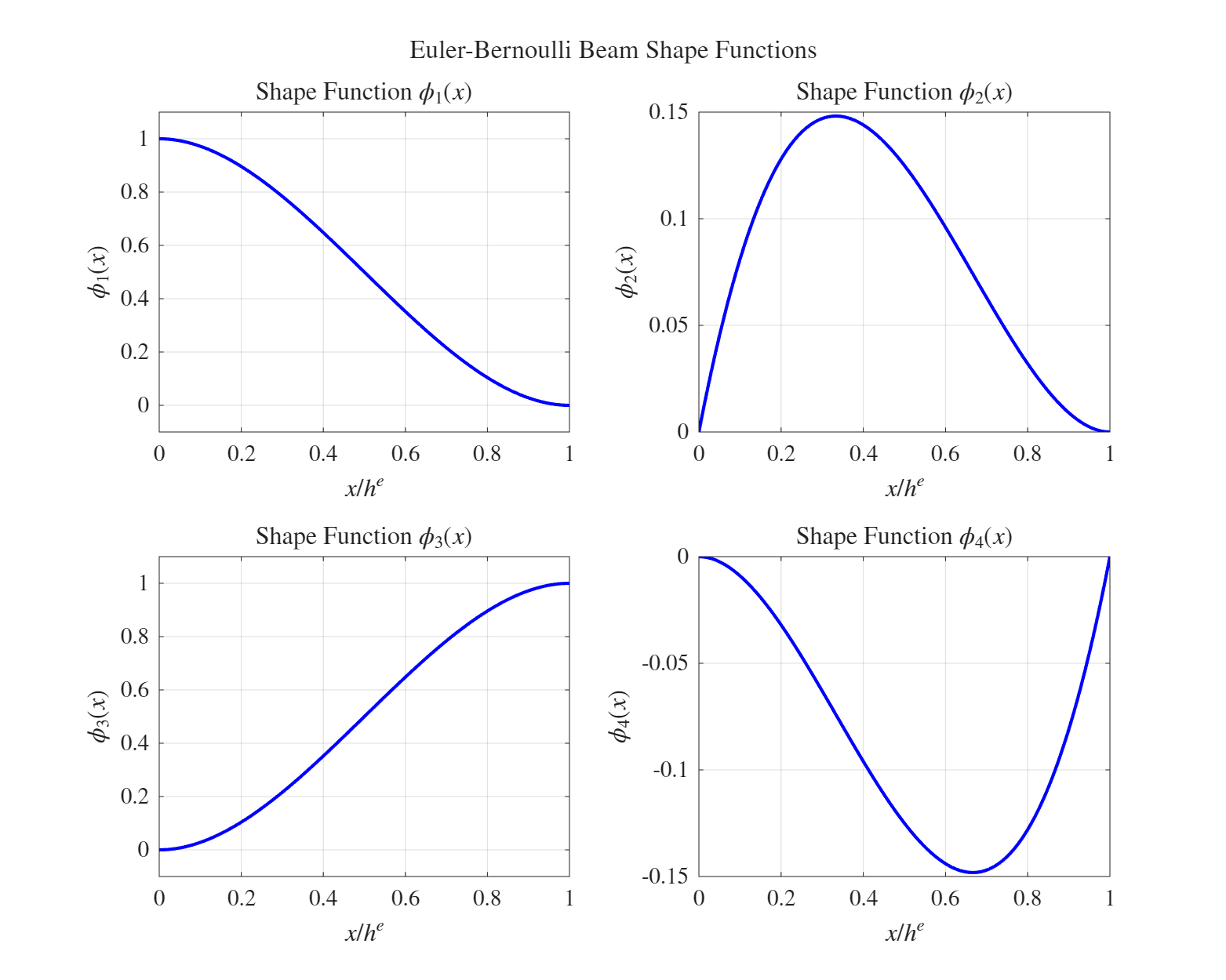
איור 10.3: פונקציות צורה עבור אלמנט ברנולי בכיפוף במישור
.
בצורה קומפקטית, התפלגות התזוזה היא:
התפלגות העיבור נובעת מהיחס הקינמטי לפי משוואה:
ניתן להחדיר בנקודה זו מטריצת
הגישה הכללית לגזירת מטריצת הקשיחות האלמנטרית, כלומר:
ניתנת לפישוט נוסף. מטריצת האלסטיות
מטריצת הקשיחות ניתנת לכתיבה על בסיס רכיבי מטריצה עבור פונקציות הצורה כדלקמן:
הנגזרות של פונקציות הצורה הבודדות במשוואה (OA5.72) נובעות ממשוואות (OA5.60) עד (OA5.63):
או לחילופין הנגזרות מסדר שני:
האינטגרציה במשוואה (OA5.72) ניתנת לביצוע אנליטי, ולאחר חישוב קצר, מתקבלת מטריצת הקשיחות האלמנטרית של קורת ברנולי בצורה קומפקטית:
בהתחשב בעומסים החיצוניים והדפורמציות המוצגות באיור, משוואת האלמנטים הסופיים העיקרית ברמת האלמנט מניבה:
בהינתן עומס מפורש
דרך נוחה יותר לחישוב היא ע”י פירוק וקטור העומס לוקטור כוחות מוכללים (כוחות ומומנטים) ומכפלת מטריצת המסה בוקטור העומסים המפורשים. כלומר, אם מקרבים את
כאשר
כמו חישוב
אלמנט קורת ברנולי עם שני מישורי דפורמציה
נתבונן כעת בקורת ברנולי שיכולה להתעוות בשני מישורים מאונכים זה לזה.
עבור כיפוף במישור ה-
כאשר וקטור הדפורמציות הוא:
ווקטור הכוחות הוא:
שתי מטריצות הקשיחות עבור הדפורמציה במישורי ה-
כאשר מטריצות הדפורמציה והעמסה מיוצגות כדלקמן:
תרגילים
תרגיל 1
בהינתן הקורה הבאה:
הקורה הנתונה.
הקורה עשויה מחומר עם מודול יאנג
פתרון:
המשוואות השולטות הן:
המשוואה שעלינו לפתור היא משוואה (OA5.83) (עבור אלמנט יחיד):
אנו כבר יודעים ש-
בנוסף, יש לנו עומסים בקצוות:
עומסים על הקורה.
לכן, וקטור העומס:
אנו יודעים מ-(OA5.82) (אנחנו באלמנט יחיד, אז אנו כבר ישרים מקבלים את המטריצות הגלובליות):
כאשר
תאכלס אכפת לנו רק משתי השורות האחרונות (ראו
ופה נמאס להם.
