שאלה 1
איור E2024.1: הבעיה הנתונה.
המשוואות השולטות:
כאשר
סעיף א’
איור E2024.2: דג”ח דיפרנציאלי של הבעיה.
סעיף ב’
נבצע אינטגרציה על (E1.1) בתחום הבעיה:
נכפיל בפונקציית בוחן
לאחר אינטגרציה בחלקים:
לאחר טיפה סידור:
סעיף ג’
נבצע את הקירובים
ו-
לפיכך, איברי מטריצת הקשיחות (הגלובלית) הם:
בצד ימין של (E1.5) נשים לב שמתקיים
אם אנו מחלקים את הגוף לשלושה אלמנטים לינאריים שווים, לאחר חישוב מטריצת הקשיחות עבור כל אלמנט, מטריצת הקשיחות הגלובלית תיבנה בצורה הבאה:
סעיף ד’
לאחר אילוץ תנאי שפה דיריכלה השמאלי ב-
סעיף ה’
זווית הפיתול היא הפתרון שלנו:
לפי עיבור הגזירה:
כאשר
מאמץ הגזירה כתוצאה מכך יהיה פשוט:
שאלה 2
איור E2024.3: אלמנט קורה בעל חמש דרגות חופש.
סעיף א’
נתון לנו:
באופן דומה ל-פיתוח בהרצאה, נקרב את
מגזירה והערכה של התפלגויות הדפורמציה
כך ש:
ולכן:
סעיף ב’
נבדוק את התנאי
נבדוק את הנגזרת (הסיבוב) בקצוות:
סעיף ג’
איור E2024.4: סכמה של פונקציית הצורה
.
סעיף ד’
אנחנו מגדירים:
כך שאנחנו למעשה יכולים לרשום:
נתון לנו כי
כעת נוכל לחשב את
בשתי נקודות גאוס
לכן:
סעיף ה’
מאחר והאינטגרנד הוא ממעלה רביעית,
סעיף ו’
מאחר והאינטגרנד יהיה ממעלה שמינית,
שאלה 3
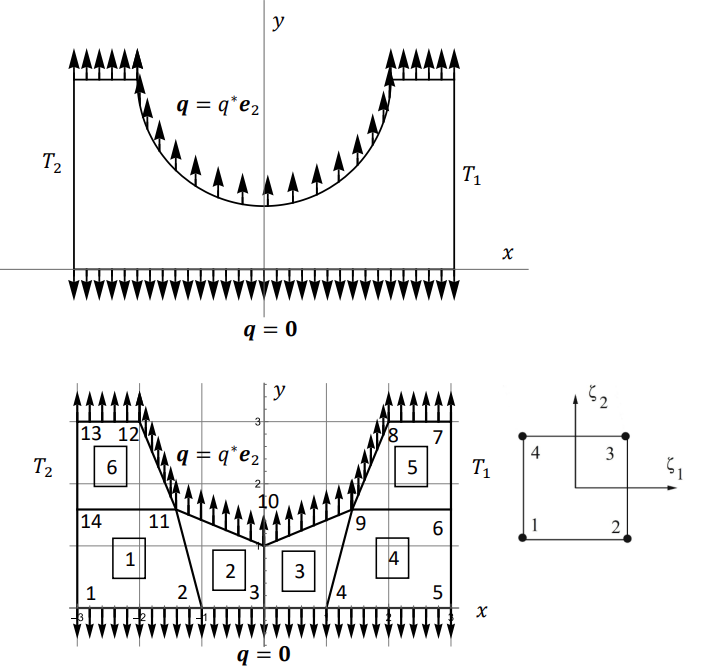
איור E2024.5: סכמת הבעיה והרישות שלה.
נתון:
סעיף א’
לפי השרטוט:
סעיף ב’
לפי הטבלה לעיל:
וכו’.
באותו אופן עבור אלמנט
סעיף ג’
יש לנו שטף אפסי בצמתים
בצמתים
כאשר
מאחר ואין כאן איבר הסעה, השטף לא משפיע על
עבור הצמתים על הקשת:
סעיף ד’
נשים לב שיש תנאי שפה דיריכלה כדלקמן:
- קצה ימני:
- קצה שמאלי:
בנוסף, כיוון שאין ייצור חום ואין
סעיף ה’
לפי מיפוי אלמנט מרובע בילינארי כללי:
אם נרצה לחשב רק את
כאשר במקרה שלנו,
נציב ב-(E3.2) כאשר נשים לב שאכפת לנו רק מ-
