SLD1_008 פיתול

→ קודם: SLD1_007הבא: SLD1_009 ←

פיתול

בפרק SLD1_005 מהלכי כוחות ומומנטים בקורות הצגנו את רעיון מומנט הפיתול- זהו מומנט בכיוון הקורה. נעסוק במקרה המציאותי בו הקורה לא קשיחה אינסופית, ומתבצעת עליה דפורמציה לאורכה. לקורה שנמצאת תחת עומס פיתול נקרא גל/גל הנע/סרן - shaft.

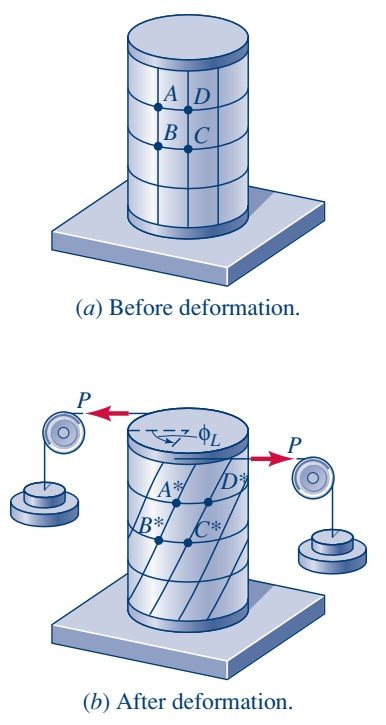
כפי שניתן לראות באיור, עבור גל עגול, כאשר הוא נמצא תחת עומס פיתול, כל חתך שלו נשאר מישורי והוא פשוט מסתובב סביב ציר הגל. לעומת זאת, עבור הגל הריבועי, החתכים של הגל מתעוותים.

דיפורמציית פיתול של גלים עגולים

ננתח את גאומטריית הדפורמציה של גלים עגולים:

נאפיין את הפיתול של גלים עגולים בשלושה הנחות:

1. ציר הפיתול נשאר ישר ולא נמתח.
2. כל שטח חתך נשאר מישורי וניצב לציר הקורה (ציר הפיתול).
3. קווים רדיאלים בשטחי החתך נשארים ישרים ורדיאלים גם במהלך הדפורמציה (קו רדיאלי - קו למרכז המעגל).

הנחות אלו מומחשות באיור הבא:

לפני הדפורמציה המישור הוא מישור רדיאלי ( ו- הם קווים רדיאליים). כאשר מופעל עליו פיתול בנקודה (בסוף), הקווים הרדיאלים ו- נשארים ישרים, אבל הם מסתובבים ל- ו-, כאשר השטחי חתך מסתובבים בזוויות פיתול בטווח ו-.

חשוב לנו להדגיש את המוסכמות לגבי סימונים. כמו בחתכים, נאמר כי מומנט הפיתול הוא חיובי, כאשר הונרמל לחתך הוא בכיוון החיובי (לפי כלל יד ימין). בנוסף, נאמר כי הזווית היא חיובית לפי כלל יד ימין:

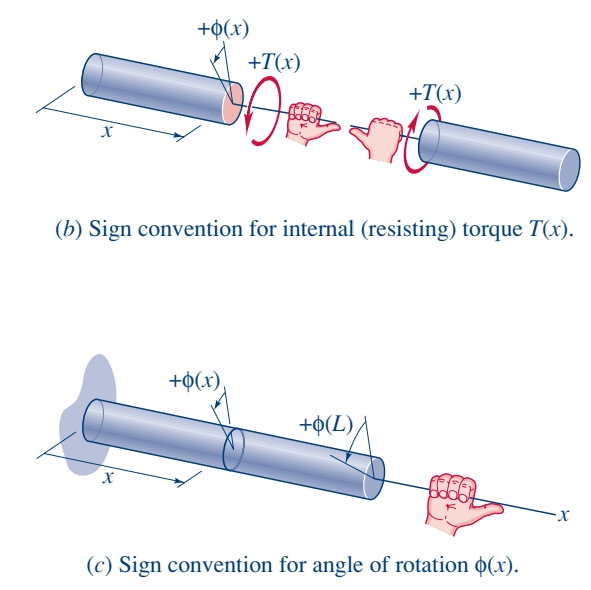
כעת נבנה קשר מתמטי בין דיפורמציית הפיתול (זווית הסיבוב ) ועיבור הגזירה .

עיבור הגזירה? מה הקשר?

ישנו קשר בין גזירה לפיתול שלא ניכנס אליו עכשיו. ניתן כעת להתעלם מהעובדה שאנו קוראים לזה עיבור גזירה, ופשוט להתייחס לעיבור זה (שהוא זווית, ולא יחס כמו בעיבור צירי) כזווית כפי שמופיעה באיורים.

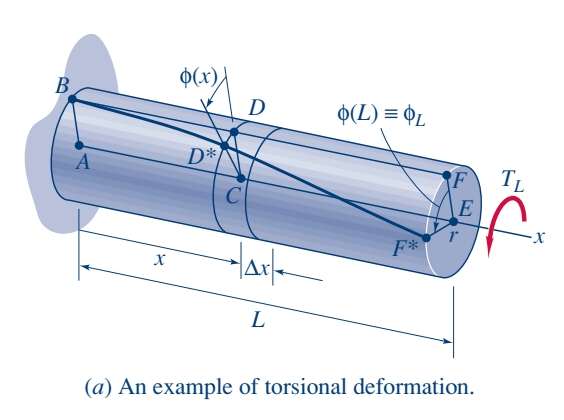
ניעזר באיור הבא:

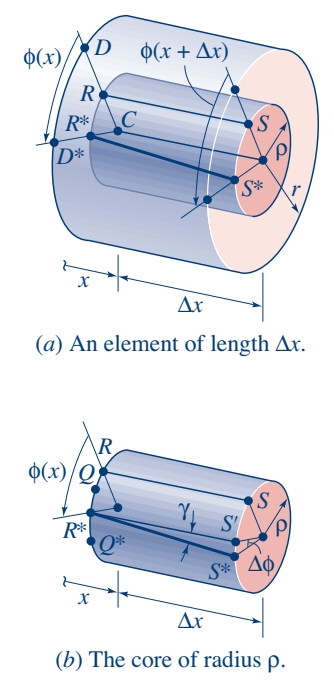
באיור זה מוצג הקטע משטח החתך בנקודה (אותו משני איורים לפני). קטע זה מפורק לגל החיצוני ולגל הפנימי - הליבה. אנו מבצעים הפרדה זו כיוון שאנו מבינים שככל שאנו מתקרבים למרכז - ציר הקורה, העומסים משתנים.
באיור אנו מתרכזים על ליבה הגל בעל רדיוס . הזווית היא זווית ישרה, שהופכת לזווית כתוצאה מהדפורמציה, שכבר לא ישרה, אלא קטנה יותר בזווית עיבור הגזירה:

מאחר והזווית מאוד קטנה, נוכל לחשב אותה ע”י קירוב של , כאשר אנו משאיפים את :

לכן:

משוואת עיבור העתק

משפט:

משוואות העיבור-העתק עבור דיפורמציית פיתול של גל עגול הוא:

כאן, הוא עיבור הגזירה בשטח חתך , במרחק מהציר. הגזירה נקראת רמת הפיתול. בנוסף, אפילו כאשר הגל העגול מורכב משני מרכיבים - גל חיצוני וגל פנימי, משוואה זו עדיין תקפה:

בנוסף נשים לב לדמיון למשוואת עיבור העתק לדיפורמצייה צירית:

פיתול של גלים עגולים אלסטיים

נביט כעת איך פיתול של גל עגול יוצר מאמץ גזירה לאורך הקורה:

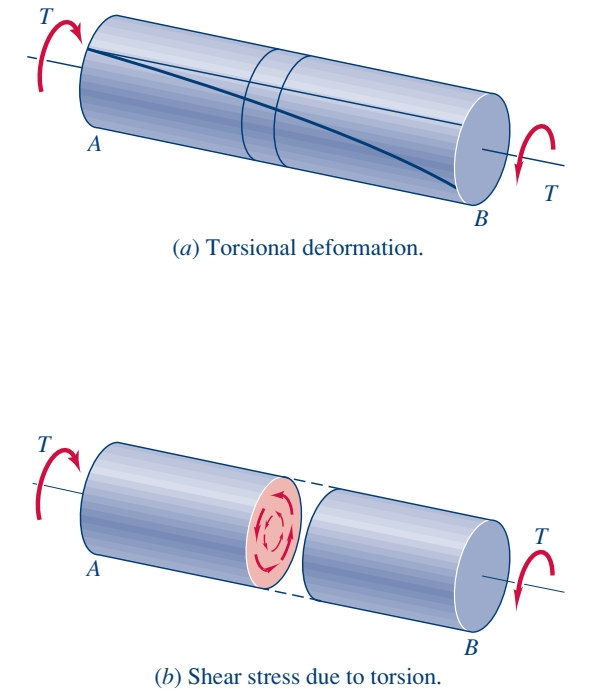
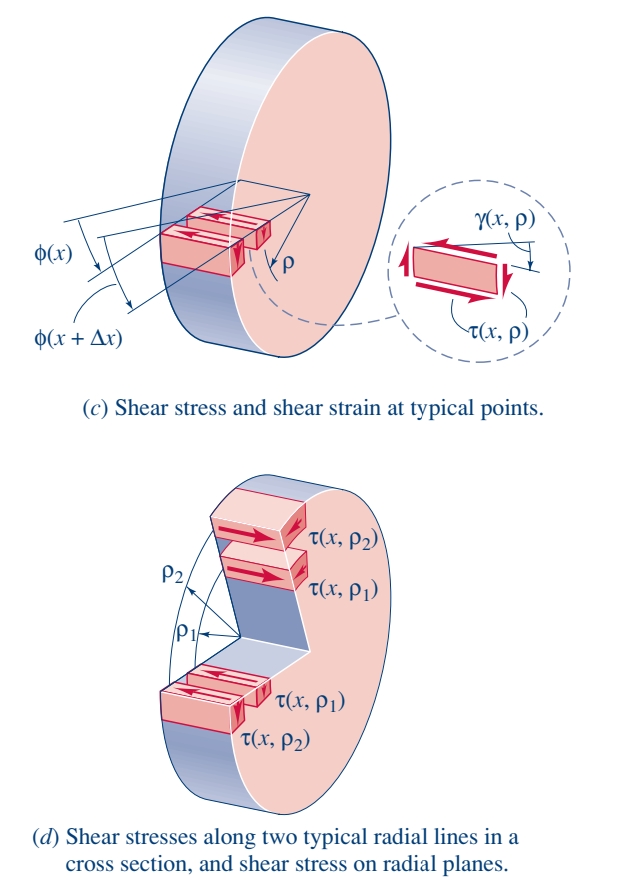
כפי שניתן לראות ב-, לאחר דיפורמציית פיתול, מלבן על שפת (וגם בתוך) הגל הופך למקבילית - מה שמעיד על דיפורמציית גזירה. בנוסף, גם בשטחי חתך עצמם ישנה גזירה!

שקול מאמץ הגזירה

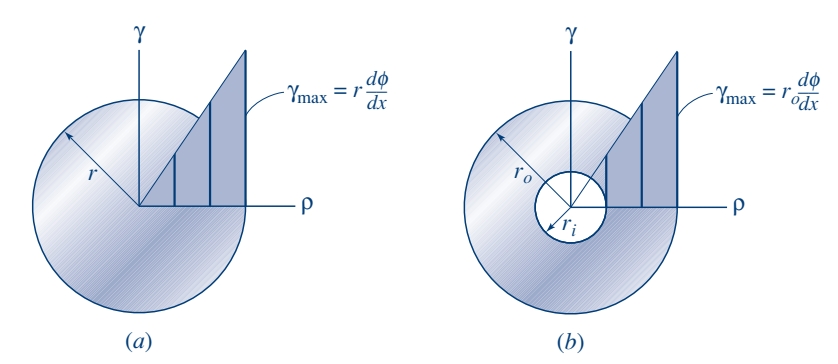
נביט באיור הבא של שטח חתך:

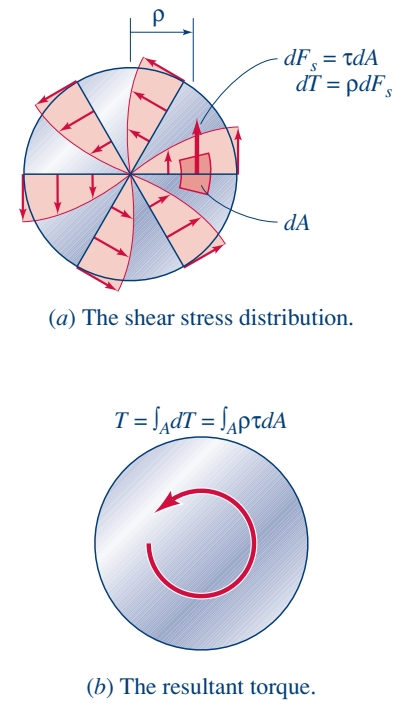
ככל שאנו מתרחקים מן המרכז, גודל כוח הגזירה, , גדל, מאחר והוא תלוי במאמץ הגזירה הפועל על שטח הגודל עם המרחק מהמרכז.

שקול מומנט הפיתול, בחתך , הוא למעשה סכום של של כל המומנטים האינפיטסימליים :

נוסחה:

חוק הוק לגזירה

כעת, כמו בדפורמציה צירית, אנו צריכים קשר בין עיבור הגזירה, ומאמץ הגזירה . בדפורמציה צירית, היה לנו את מודול יאנג:

גם לדיפורמציית פיתול, ישנו טווח מאמצים בחומר, הטווח האלסטי, בו ישנו קשר בין ל-:

נוסחה:

כאשר הוא נקרא מודול הגזירה. נציב במשוואה זו את משוואת עיבור העתק:

נקבל ממשוואה זו את הקשר בין מאמץ הגזירה, למרחק ממרכז המוט. אם המוט הומוגני, כלומר , אז מאמץ הגזירה משתנה לינארית עם המרחק ממרכז הגל, כאשר המאמץ המקסימלי מתקבל על שפת שטח החתך (גם אם הגל חלול):

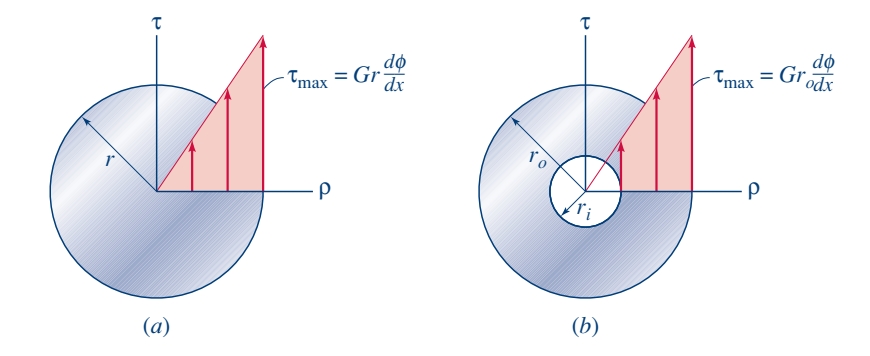
מומנט אינרציה

עבור המקרה הפרטי של אלסטיות, ניתן למצוא מ-שקול מאמץ הגזירה ו-חוק הוק לגזירה ש:

אם לא תלוי ב-:

ניתן לאינטגרל הימני שם:

או, לפי סימוני הקורס:

הגדרה:

מומנט האינרציה הפולארי מוגדר כהאינטגרל:

מאחר וזהו למעשה אינטגרל כפול על מעגל, נמצא כי עבור רדיוס :

משוואת פיתול-רמת פיתול

הצמד נקרא קשיחות פיתולית - כמה קשה לנו לסובב את המוט. נציב את משוואת עיבור העתק, כדי לקבל את משוואת הפיתול-רמת פיתול:

או, לפי סימוני הקורס:

נוסחה:

משוואת פיתול-זווית פיתול

מהמשוואה הקודמת, עבור זווית פיתול בין נקודה לנקודה , כאשר , ומוט הומוגני, השינוי בזווית הפיתול היא:

נוסחה:

משוואת דיפורמציית פיתול

אם נציב את (1) במשוואה הקודמת, נקבל:

או לפי סימוני הקורס:

נוסחה:

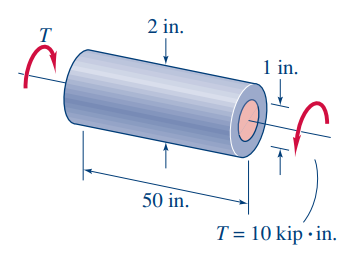
דוגמה:

גל העשוי מקליפת אלומיניום () וליבת פלדה () המרותכים אחד לשני. ממדי הגל:

בנוסף, מופעלים עליו בקצוותיו מומנטי פיתול בגודל .

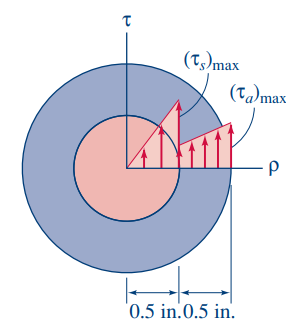
• מצאו את המאמץ הגזירה המקסימלי בליבת הפלדה ומאמץ הגזירה המקסימלי בקליפת האלומיניום.
  פתרון:
  נשים לב כי מאחר ושני החלקים של הגל מתפתלים ביחד, רמת הפיתול שלהם שווה:

נציב במשוואת דיפורמציית פיתול:

לכן, נוכל להסיק כי רמת הפיתול היא:

נציב את הנתונים:

כלומר, רמת הפיתול היא רדיאנים לכל שינוי של אינץ’ .
נציב בחזרה ב-(1):

• מצאו את זווית הפיתול הכללית של הגל.
  פתרון:
  אנו לא יכולים להשתמש במשוואת פיתול-רמת פיתול מאחר והיא מתייחסת למוטות הומוגניות. אבל, מאחר ורמת הפיתול זהה לאורך כל המוט, נוכל:

תרגילים:

1. נתון:
   
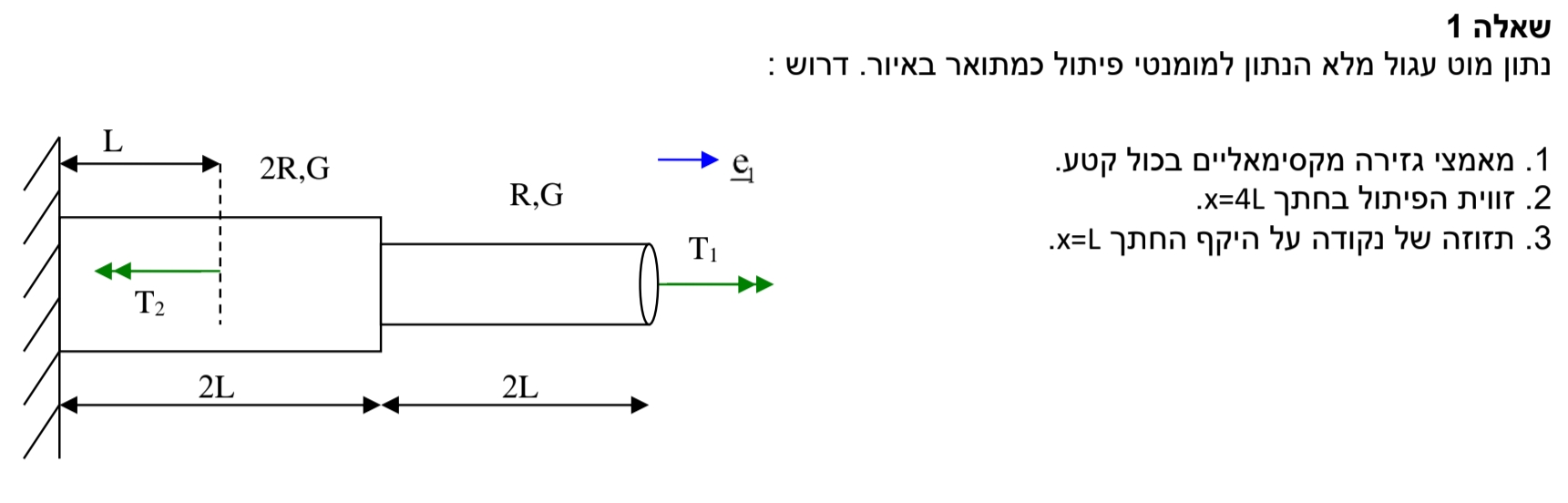
   נבחר ראשית צירים בפינה השמאלית. דג”ח על חתכים לאורך הדגם:
   
   פתרון:
   נביט בכל חתך: כעת מבקשים מאיתנו את זווית הפיתול ב-. אז נסכום את כלל הזוויות פיתול (השינויים) בכל מקטע: נמצא את התזוזה של נקודה ב-. מאחר ואלו הן תזוזות קטנות, נוכל להתייחס רק לתנועה הקווית:
   נמצא את : נציב, ונסיק כי:

→ קודם: SLD1_007הבא: SLD1_009 ←