פנגייה

FLD1_009 שכבות גבול

• זמן קריאה: 13 דק'

מבוא

בזרימה סביב גליל חישבנו את פילוג הלחצ’ים על שפת הגליל:

במשפט קוטה-ז’וקובסקי פיתחנו מפילוג לחצים זה את העילוי - הכוח בכיוון . נוכל באותו אופן לחשב את הכוח בכיוון :

ונקבל לאחר קצת אלגברה ש:

יש לנו כאן בעיה. בעצם חישבנו כאן שעבור גליל שנמצא בזרימה מציפה, לא פועל עליו כוח בכיוון הזרימה - מה שאנו קוראים לו כוח גרר. אבל, ברור לנו שבעולם הפיזיקלי אם נשים גליל, או כל צורה אחרת תחת שדה זרימה מציפה, כמו למשל כדור בבריכה - הזורם יפעיל כוח על הכדור, ויגרום לו לזוז בכיוון תנועת הזורם.

כלומר, יש לנו אי הסכמה מובהקת בין התאוריה לפרקטיקה - ולאי הסכמה זו קוראים פרדוקס דלמבר.

עצם הופעת פרדוקס זה נובע מההזנחות שביצענו. ברגע שהזנחנו את הצמיגות עבור זרימה אינרציאלית, וויתרנו על אחד מתנאי השפה - תנאי האי-החלקה. מסתבר שוויתור זה הוא מאוד בעייתי, כי עבור רוב הגאומטריות אי-ההחלקה הוא תנאי לא יציב במשוואות נאוויה-סטוקס - הזנחה שלו עשויה להוביל לתוצאה שונה לגמרי.

כדי לפתור את הבעיה הזאת, במקרה הפשוט של פלטה דקה תחת זרימה מציפה, אנו מחלקים את הזרימה לשלוש:

  1. זרימה רחוקה מהגוף - הרחק מהגוף משוואות הזרימה האינרציאלית/פוטנציאלית עדיין תקפות.
  2. זרימת שכבת גבול למינרית - אזור דק וקרוב מאוד לגוף בו גם האינרציה וגם הצמיגות דומיננטיים בזרימה, אבל עדיין הזרימה למינרית (שכבתית, באותו הכיוון, מקבילה).
  3. זרימת שכבת גבול טורבולנטית - גם כן אזור קרוב לגוף, בו גם כן גם האינרציה וגם הצמיגות דומיננטיים, אבל הזרימה בו טורבולנטית (כאוטית).

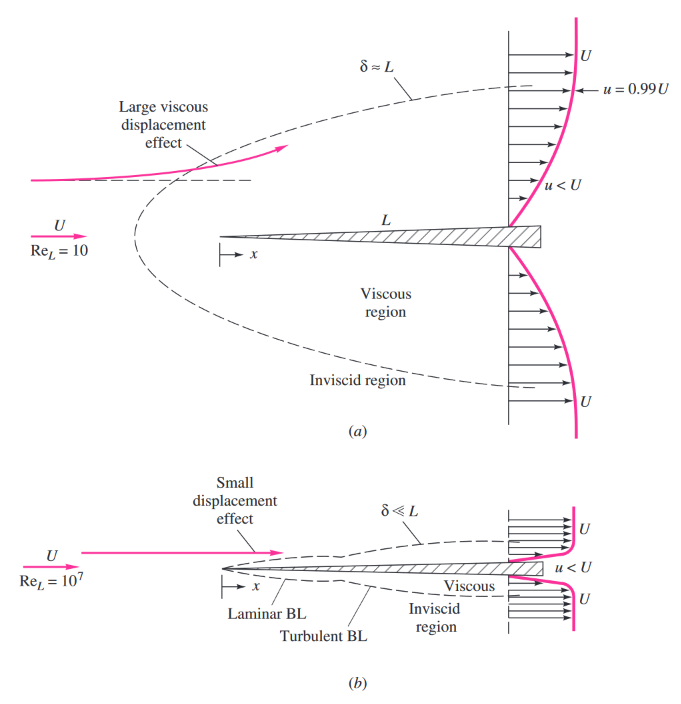
bookhue

זרימה מציפה על פלטה חדה במספרי ריינולדס שונים. (a) זרימה שכולה למינרית, בריינולדס קטן; (b) זרימה בריינולדס גבוה, כך שנוצרה גם שכבת גבול טורבולנטית. (White & Xue, 2021)

בעזרת הגדרת שכבת הגבול, נוכל לחשב את אפקטי הצמיגות ליד גוף קשיח (וכך למשל לחשב את כוח הגרר) ואז “לתפור” אותו לזרימה האינרציאלית החיצונית.

בקורס לא נתמקד בשכבת הגבול הטורבולנטית, אלא רק באזור הלמינרי, היותר פשוט.

חשוב לשים לב ששיטה זו, הנקראת תאוריית שכבת הגבול, כושלת בתיאור הזרימה סביב גופים קהים (גם אם ריינולדס מאוד גבוה):
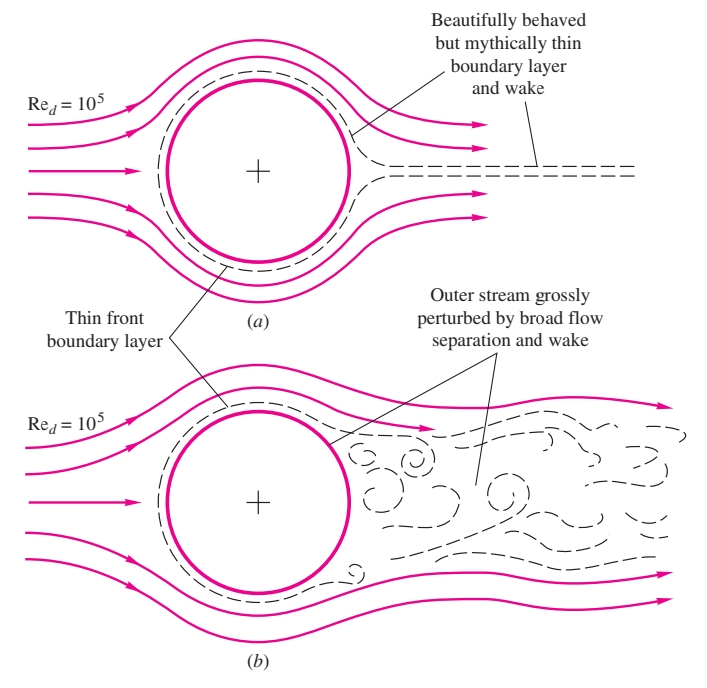
bookhue

שדה זרימה סביב גליל - גוף קהה (blunt body). (a) תיאור אידיאלי, אבל למעשה לא נכון, של שדה הזרימה סביב גוף קהה; (b) תיאור יותר מדויק של זרימה סביב גוף קהה. (White & Xue, 2021)

זרימה סביב גליל בריינולדס (Van Dyke, 2008)

באיור האידיאלי, ישנה שכבת גבול דקה סביב הגוף. אבל, בזרימה אמיתית, שכבת הגבול אמנם דקה בקדמת הגליל, הפוגש את הזרם ראשון. אבל, בחלקו האחורי, שכבת הגבול נפגשת באזור בו הלחץ עולה, ומתנתקת לאזור הנקרא wake. הזרימה משתנה עקב היווצרות אזור זה, באופן שונה מאיך שתאוריית שכבת הגבול חוזה אותה.

עובי שכבת הגבול

השכבות גבול, בין אם למינריות או טורבולנטיות הן מאוד דקות, אפילו יותר דקות מכפי שמתואר באיורים. אנו מגדירים את עובי שכבת הגבול כהגובה מעל הפלטה בו מהירות הזורם המקבילה לפלטה מגיעה ל- ממהירות הזרימה המציפה .

פאול בלסיוס הראה (בעזרת פיתוחים מתמטיים ארוכים) שגובה זה (עבור האזור הלמינרי) נתון ע”י:

כאשר הוא מספר ריינולדס בו הוא הגודל האופייני. כלומר, משתנה לפי .
bookhue

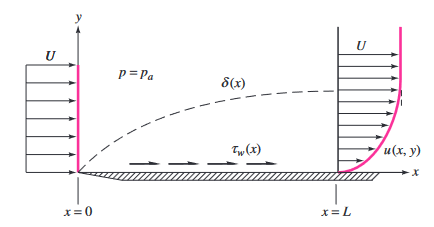
גדילת שכבת הגבול על פלטה שטוחה. העובי הוגזם בשביל נוחות התיאור. (White & Xue, 2021)

פרופיל שכבת גבול בלסיוס על פלטה שטוחה (Van Dyke, 2008)

קירוב פון קרמן

עובי שכבת מומנטום

נביט שוב באיור על עובי שכבת הגבול על פלטה שטוחה:
book

בחירת נפח בקרה על פלטה שטוחה

כיוון שאנו מניחים שבאזור המסומן (שכבת הגבול) הצמיגות לא זניחה, אז מתקיים עדיין אי-החלקה, מה שגורם לפרופיל מהירות מעוגל . בהמשך נמצא את פרופיל זה, אבל כעת נוכל להסתפק בשימור תנע אינטגרלי כדי למצוא למשל את כוח הגרר על הפלטה.

נבחר את נפח הבקרה שלנו כמתואר באיור, כאשר גובהו מוגבל ב-. לפי שימור התנע האינטגרלי, אנחנו נקבל שסך הכוח שהזורם מפעיל על הפלטה במרחק כלשהו הוא:

כאשר הוא עובי הפלטה (לתוך המסך), והאינטגרציה מתבצעת מ- עד גובה שכבת הגבול .
משוואה זו פותחה ע”י פון קרמן, והוא כתב אותה בצורה קצת שונה, שהיא המקובלת יותר - עובי שכבת המומנטום:

כאשר .
השם מבלבל, כי זה בעצם לא עובי, אלא מידה לרמת הגרר על הפלטה.

אינטגרל פון קרמן

קרמן גם שם לב שכוח הגרר הוא גם אינטגרציה על מאמץ הגזירה לאורך הפלטה:

כאשר הסימון על מעיד על כך שמדובר במאמץ הגזירה על הפלטה - ב-.
משתי משוואות אלו, ניתן למצוא את מאמץ הגזירה על הפלטה, מה שנקרא קשר התנע האינטגרלי לפלטה שטוחה בזרימת שכבת גבול, או פשוט משוואת פון קרמן:

במקרה היותר כללי בו יכל להיות תלוי ב- (זה המקרה כמעט בכל זרימה שהיא לא זרימה על פלטה) ויניקה :

נחזור למקרה היותר פשוט של פלטה שטוחה.
בקורס אנו לרוב נניח, כמו קרמן, שפרופיל המהירות הוא פרבולי, למשל מהצורה:

בעזרת הנחה זו, ניתן לקבל קירובים מאוד טובים ל-:

ולכן, לפי יחס התנע האינטגרלי:

מהגדרת מאמץ הגזירה, אנו גם יודעים ש:

ספציפית על הפלטה:

נשווה בין הערכים השונים שקיבלנו ל-:

נבצע אינטגרציה על שני צדי המשוואה ונקבל:

הביטוי בתוך האינטגרל הוא למעשה :

כלומר, קיבלנו קירוב לגובה שכבת הגבול דרך הנחה שפרופיל המהירות הוא פרבולי. ראינו, שבלסיוס הראה, שביטוי יותר מדויק הוא , וגם , אבל בקורס אנחנו בעיקר נניח שהפרופיל הוא פרבולי כי זה הרבה יותר פשוט מאשר הפיתוחים שבלסיוס ביצע.

עובי הזזה

עוד תוצאה מעניינת של שכבת הגבול היא הזזה קטנה וסופית של קווי הזרם החיצוניים.

book

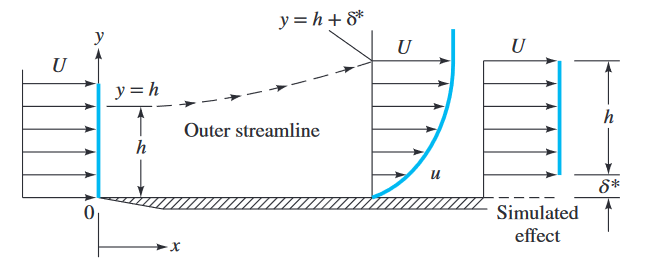
אפקט ההזזה של שכבת גבול (White & Xue, 2021)

כדי לקיים שימור מסה, הקווי זרם החיצוניים חייבים לנטות החוצה במרחק כדי לקיים שימור מסה בין הכניסה והיציאה:

כאשר . הגודל נקרא עובי ההזזה של גבול ההזזה. לאחר קצת אלגברה, ניתן לקבל ממשוואה זו ש:

לכן, היחס תלוי רק בצורת פרופיל המהירות החסר הממדי . אם נציב את הקירוב הפרבולי ל-, נקבל ש:

שהוא למעשה קירוב לא רע, אם נשווה לחישוב יותר מדויק שבלסיוס ביצע - .
כיוון ש- הרבה יותר קטן מ- עבור גדולים, ושיפוע קו הזרימה פרופורציונלי ל-, נסיק שהמהירות בכיוון הנורמלי לפלטה הרבה יותר נמוך מהמהירות המקבילה לפלטה.

משוואות שכבות הגבול

בשכבות גבול יש חשיבות גם לאינרציה וגם לצמיגות, אבל ברוב המקרים נוכל להזניח את כוחות הגוף. בהנחות אלו, משוואות נאוויה-סטוקס המנורמלות מקבלות את הצורה (שעדיין מאוד מסובכת):

משפט:

משוואות שכבות הגבול קובעות כי עבור זורם, בשכבת הגבול, מתקיים (במקרה הדו-ממדי):

כאשר הם רכיבי שדה המהירות; הוא צפיפות הזורם; הוא שדה הלחצים בזורם; הוא הצמיגות הקינמטית שהיא היחס בין הצמיגות לצפיפות ; ו- הוא המהירות מחוץ לשכבת הגבול.

פיתוח:
ממשוואות נאוויה-סטוקס הדו-ממדיות בכיוון :

השפעות הכוחות גוף לרוב זניחות בגאומטריות הדקות של שכבות גבול, כך שנזניח אותם:

באותו אופן כמו הנחת גופים דקים, נוכל לנרמל את המשוואה לפי , כאשר הוא הגובה האופייני של שכבת הגבול ו- הוא האורך האופייני של שכבת הגבול. מנרמול זה, ניתן להראות ש- זניח:

נחלק ב-:

את נקבל באותו האופן (מאוד דומה גם לקירוב הלובריקציה).

כיוון ש- , אם נמצא את מחוץ לשכבת הגבול (באזור האינרציאלי), ביטוי זה יהיה גם נכון עבור שכבת הגבול. במקרה הדו-ממדי, בו אנו מזניחים כוחות גוף, משוואות האינרציה בכיוון הן:

נציב ב-(1) ונקבל:

הערה:

שכבת גבול (הלמינרית) בהגדרתה דקה. הניתוקים והזרימות הטורבולנטיות שמתרחשות למשל בזווית התקפה מאוד גבוהה בכנף הם מה שקורה כאשר שכבת הגבול נהרסת. לא נעסוק בשכבת גבול עבה - הרי בהגדרתה היא תמירה.

תנאי שפה על שכבות גבול

תנאי השפה שלנו עבור הזרימה בשכבת גבול ומהירות חיצונית (כלומר, עשויה להשתנות לפי . אם מדובר בפלטה שטוחה, אז ).

  1. מאי-החלקה:

  2. מעצם הגדרת שכבת הגבול (גם אם משתנה):

  3. השפה העליונה של שכבת הגבול היא שפה חופשית (אין עליה כוחות גזירה), ולכן:

  4. ניתן להראות ממשוואות שכבות הגבול ב-, שעל הקיר, במקרה בו הפלטה שטוחה (כי אז ), ואין יניקה, הנגזרת השנייה של מקיימת מתקיים:

הערות:

  1. אם לא מדובר בהכרח בפלטה שטוחה, אפשר למצוא את התנאי שפה מהצבת במשוואות שכבת הגבול.
  2. אם צריכים, אפשר לדייק יותר את הקירוב שלנו עם תנאי רציפות על נגזרות הזורם בגבול בין שכבת הגבול לזרימה החיצונית. כלומר:
  1. לפעמים, אם נתון סך כוח הגרר, או שדרוש למצוא את כוח הגרר, כדאי להשתמש בהגדרת מאמץ הגזירה על הקיר כעוד תנאי שפה:

עבור , מאי חדירה:

תרגילים

שאלה 1

נתונה זרימה למינרית סביב לוח מלבני באורך , רוחב . נקרב את פרופיל המהירות באופן פרבולי:

כאשר .

סעיף א’

מצאו את המקדמים בעזרת שיטת von-karman.

פתרון:
תנאי השפה שלנו על :

לפני שנעבור לתנאי השפה הבאים, נשים לב ש:

ולכן

ולכן, מהתנאי שפה , נסיק כי:

עוד תנאי שפה (תנאי שפה מספר (5))הוא (כי ). נשים לב כי:

נציב את התנאי שפה:

מכל ארבעת תנאי השפה נקבל:

נציב הכל בחזרה ב- ונקבל:

סעיף ב’

מצאו את עובי שכבת הגבול הבלתי ממדי, בצורה .

פתרון:
נחשב את :

נשים לב שהביטוי בתוך האינטגרל שווה לאפס כאשר , כי אז (מהירות הזורם הוא פשוט מהירות הזרימה המציפה). לפיכך, נכול לצמצם את האינטגרציה לתחום :

לכן, לפי לפי פון קארמן:

מהגדרת מאמץ הגזירה (כלומר, מאמץ הגזירה על הפלטה):

נשווה ונקבל:

זוהי משוואה דיפרנציאלית. נפתור אותה:

נקבל כי:

סעיף ג’

מהו מאמץ הגזירה על הפלטה ?

פתרון:
נציב את הפתרון שקיבלנו בחזרה ב-:

או, בצורה היותר מקובלת (נשים לב כי ):

סעיף ד’

מהו הגרר על הפלטה?

פתרון:
נבצע אינטגרציה על כל אורך הפלטה:

שאלה 2

נוזל בלתי דחיס בעל צמיגות קינמטית זורם לתוך תעלה דו-ממדית בעלת גובה עם מהירות אחידה . הניחו שכבת גבול למינרית עם הפרופיל שמצאת בשאלה הקודמת.
book

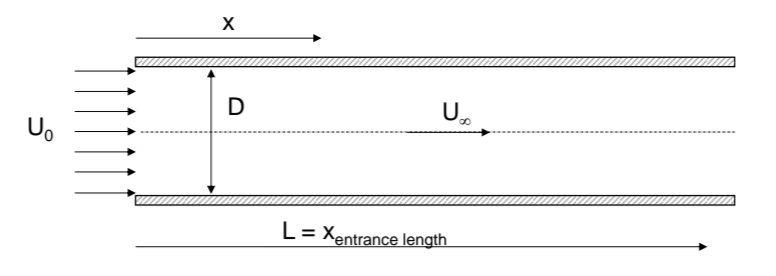
סכימת הזורם

סעיף א’

מצאו את “אורך הכניסה” , כלומר, את המרחק האופקי שבו הזרימה הופכת להיות מפותחת בכיוון . יש להניח כי (קבועה).

פתרון:

על שני צדי התעלה תתפתח שכבת גבול, עד הרגע בו שתי שכבות הגבול יפגשו אחת את השנייה, ומ- זה, כל התעלה היא שכבת גבול.

מה- המתואר בציור, בו , נוכל לומר שהזרימה מפותחת (מכל מיני פיתוחים וגם העובדה שהגאומטרייה תמירה).
משאלה קודמת, סעיף א’, אנו יודעים ש:

לכן, באורך הכניסה - . נציב:

נקבל כי אורך הכניסה הוא:

סעיף ב’

כאשר הזרימה היא מפותחת, ניתן לראות כי , אלא . הוכיחו את התוצאה הזאת.

פתרון:
נבצע שימור מסה אינטגרלי על הכניסה, ועל הסוף של התעלה:

ולכן .

עמודים המציינים את העמוד הזה