FLD1_E2023WA 2023 חורף מועד א'

שאלה 1

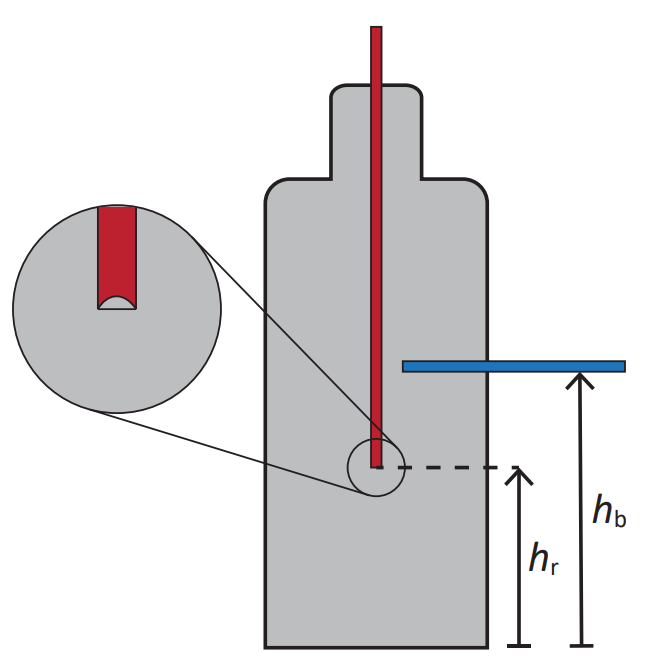
סכמת הבעיה

סעיף א’

מהידרוסטטיקה תחת כבידה:

נגדיר את ראשית מערכת הצירים שלנו בתחתית הבקבוק. מאחר ובקש האדום יש לחץ אטמוספרי:

נציב בחזרה ב-:

סעיף ב’

מתח פנים לא בחומר.

סעיף ג’

כדי שלא תתרחש זרימה אל מחוץ לבקבוק, נדרוש שלחץ המים בגובה הקש הכחול, , יהיה קטן מהלחץ האטמוספירי, :

נמצא את בעזרת סעיף א’:

שאלה 2

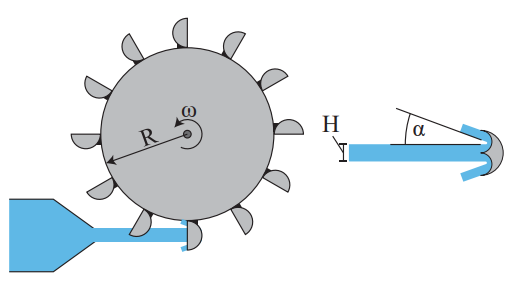
סעיף א’

נחשב עבור המקרה הכללי בו הגלגל כן מסתובב (נצטרך את זה בסעיף ב’), ואז פשוט נציב . מהירות הסל החיצוני (אותו נבחר כהנפח בקרה):

למרות שהנפח בקרה זז, נבחר מערכת צירים קבועה.

בחירת נפח הבקרה (שזז) ומערכת צירים קבועה.

לפי שימור תנע אינטגרלי:

כאשר היא המהירות של הזורם ביחס למערכת הצירים ו- היא המהירות של הזורם ביחס לנפח הבקרה.
נוכל להניח כי המצב תמידי (נתון מהעובדה שהזרם פוגע בסל כל הזמן), כך ש- . בנוסף, נביט רק בכיוון :

אין כוחות גוף בכיוון , אז נישאר רק עם הכוחות שפה (סכימה של המאמצי גזירה):

נסמן את כוחות שפה אלו ב- - הכוח שהסל מפעיל על הזורם. בנוסף, נפרק את האינטגרל הימני לאינטגרל על כניסת ויציאת הנוזל:

נחשב כל אינטגרל בנפרד:

• בכניסה, המהירות של הזורם ביחס לנפח בקרה , והמהירות ביחס למערכת הצירים הם:

  ולכן, בכניסה:

  נשים לב כי , ולכן:

  כאשר הוא השטח של זרימת הכניסה.

• ביציאה, נניח ששטח כל אחת מהנתזים שיוצאים מהסל שווה ל- , אחרת אי אפשר לפתור את הבעיה (יענו חסר לנו כאן נתון). לכן, משימור מסה אינטגרלי:

  מסימטריה, גודל מהירות הנתז העליון שווה למהירות הנתז התחתון. לכן, כאשר נפתח את האינטגרלים, נקבל:

  נסדר טיפה:

  לכן, עבור הנתז העליון, המהירות ביחס למערכת צירים קבועה היא:

  המהירות ביחס לנפח בקרה היא:

  והנורמל הוא:

  נשים לב ש:

  באותו האופן עבור הנתז התחתון.
  נוכל כעת לחשב את האינטגרל של התנע ביציאה:

  כאשר הביטוי הראשון בצד ימין של המשוואה מתאר את התנע של הנתז העליון, והביטוי השני בצד ימין של המשוואה (כלומר, השורה השנייה), מתאר את התנע של הנתז התחתון - בכיוון . נסיק כי:

  הערה:

  בפתרון הרשמי יצא להם:

  לא יודע אם הבעיה אצלי או אצלם. נזרום עם הפתרון שלהם.

נציב את (2) ו-(3) בחזרה ב-(1) ונקבל:

לכן, הכוח שהנוזל מפעיל על הסל הוא , כך שהמומנט שמופעל על הסל הוא:

במקרה בו , נקבל כי:

במקרה הכללי יותר, ההספק שנוצר מהגלגל הוא:

סעיף ג’

מפתרון סעיף קודם, נקבל גודל מקסימלי כאשר , כי אז .

סעיף ד’

נציב בביטוי הכללי ל- שמצאנו בסעיף א’:

שאלה 3

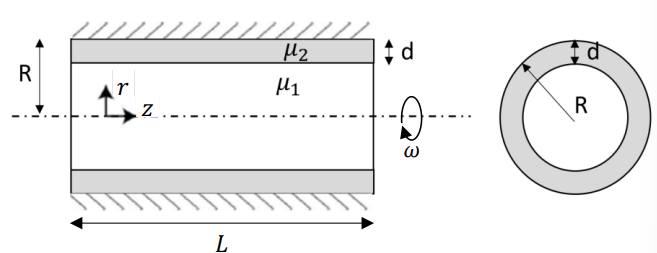
סכימת הזרימה בגליל

סעיף א’

כדי להזניח אינרציה (ביחס לצמיגות) נדרוש ש- . בנוסף, כדי להזניח כבידה (ביחס לצמיגות), עלינו לדרוש גם ש - .

סעיף ב’

סיבוב הגליל סביב צירו יוצר כוחות גוף למרכזו. מאחר והזנחנו אינרציה, וגם , נישאר עם משוואות ההידרוסטטיקה, רק עם הכוחות גוף (במקרה שלנו, כוח מדומה - כוח צנטריפוגלי במערכת הצירים המסתובבת):

במערכת הצירים המסתובבת, , ולכן:

נסיק כי לנוזל הקרוב יותר למרכז הגליל (נוזל ) יש צפיפות נמוכה יותר - גרדיאנט הלחצים דורש זאת. הרעיון דומה לכך ששמן צף מעל מים, אבל הפעם “כוח הכבידה” פועל לכיוון החוצה ממרכז המעגל.

סעיף ג’

התנאים הנתונים הם בדיוק התנאים הדרושים למשוואות הלובריקציה בקואורדינטות גליליות:

הערה:

בסעיף קודם קיבלנו ש-, ועכשיו אנחנו טוענים שהוא שווה לאפס. הסיבה בהבדל הוא שאנחנו למעשה מזניחים את הגודל . כלומר, מהעובדה שהגאומטרייה תמירה, ישנם הבדלים הרבה יותר דומיננטיים בכיוון בלחץ, מאשר בכיוון .

בנוסף, לפי משוואת הרצף בקואורדינטות פולאריות:

התנאי שפה על הם:

1. אי-החלקה על שפת הגליל:
2. אי חדירה על הגליל:
3. רציפות במהירות בין זורם לזורם :
   4. רציפות במאמצי הגזירה בין זורם לזורם :

סעיף ד’

נניח את ההנחות הבאות:

1. הבעיה אקסיסימטרית - .
2. הזרימה מפותחת (ניתן להסיק זאת מהעובדה שתנאי השפה לא משתנים ב-, ושאנו בקירוב הלובריקציה) - .
3. כוחות גוף זניחים.

ממשוואת הרצף בסעיף קודם:

מתנאי השפה , נסיק כי , כך ש:

כלומר, טענה מספר (4):
4. המהירות בכיוון אפסית - .

ממשוואת הלובריקציה בכיוון :

מאחר ו- לא תלוי ב-, נוכל להתייחס אליו כקבוע באינטגרציה לפי :

הביטוי בעייתי - כאשר , הוא שואף ל-, מה שבוודאות לא נכון. נסיק כי , ואז:

נפרק את שדה הזרימה לכל אחד מהזורמים השונים:

נתחיל מזורם . על הקיר, אנו יודעים ש:

ולכן:

עבור זורם , נשתמש ברציפות שלו עם זורם :

נציב בחזרה בביטוי ל-:

סעיף ה’

פרופיל זורם הוא פרבולי, ויש לו אי החלקה ב- . ככל יותר גדול, כך קצב שינוי הפרופיל שלו יותר קטן.

השוואת פרופילי המהירות עבור יחסים שונים בין הצמיגויות של הזורמים.

הערה:

אני חולק על התשובות במבחן.

הדגמה של שתי פרופילי המהירויות השונות. הגרף אינטראקטיבי - ניתן לשנות את .

שאלה 4

זהה לשאלה 2 מהתרגול.