HTF1_HW007 תרגיל בית 7

	סטודנט א’
שם	עידו פנג בנטוב
ת”ז	CLASSIFIED
דואר אלקטרוני	CLASSIFIED

שאלה 1

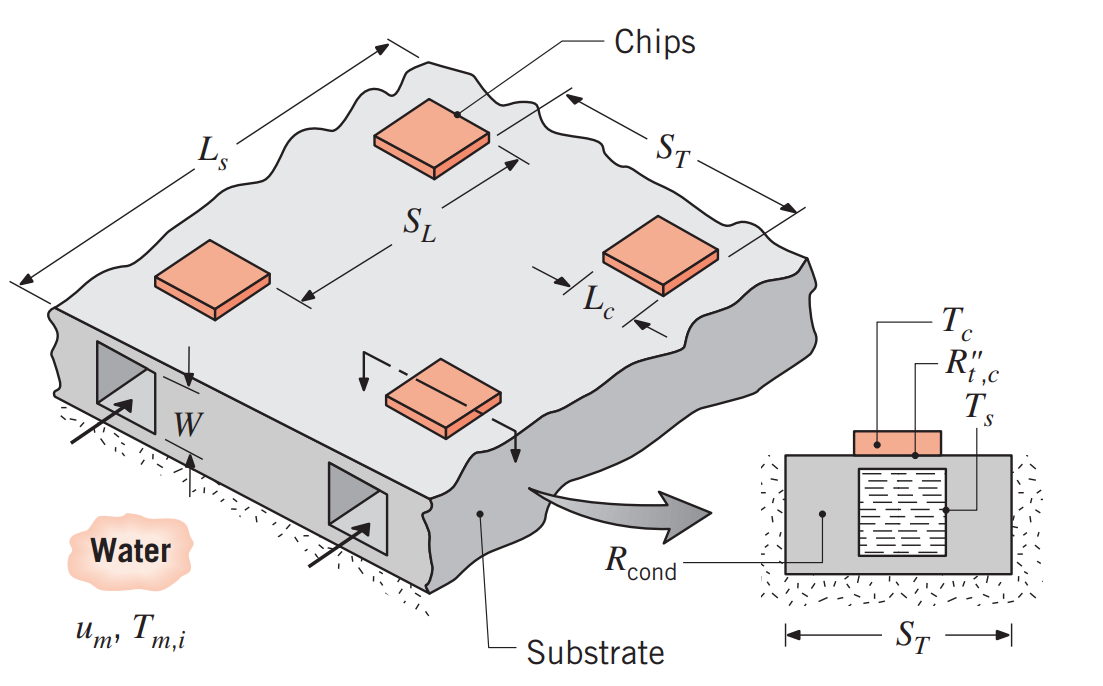
סכמת הבעיה.

נתונים תכונות המים:

התעלות והשבבים:

אורך הלוח:

מהירות הזורם והטמפרטורה בכניסה:

סעיף א’

מניחים כי כל שבב מפזר ( עבור chip).

הנחות:

1. מצב מתמיד.
2. זרימה חד ממדית (בכיוון התעלה).

נתון לנו הספק חום שנכנס למערכת ושואלים אותנו על הטמפרטורה הסופית. לכן, נשתמש בחוק ראשון על התעלה:

נכנס לנו הספק חום מהשבבים, ומהמים הנכנסים. יוצא לנו הספק חום מהמים שיוצאים. אין ייצור חום פנימי, ואנו במצב מתמיד, לכן:

נשים לב ש- :

נציב נתונים:

סעיף ב’

נרצה לדעת האם אנו בזרימה למינרית/טורבולנטית. הקוטר האפקטיבי לצינור בשטח חתך ריבועי, לפי משוואה (IH8.66):

לכן מספר ריינולדס הרלוונטי הוא:

כך שאנו בזרימה טורבולנטית.
גם במקרה של צינור בשטח חתך ריבועי, מומלץ להשתמש בקורלציה לזרימה מפותחת טורבולנטית. נבחר בקורלציה המתאימה לתנאי הבעיה, משוואה (IH8.62):

כאשר את מקדם החיכוך אנו נוציא ממשוואה (IH8.21):

נציב גם את שאר הנתונים ונקבל:

לכן מקדם ההסעה:

סעיף ג’

נתון ש:

נשרטט דיאגרמת נגדים:

דיאגרמת נגדים על הבעיה הנתונה.

נחשב את ההתנגדות הכללית:

לפי משוואה (IH8.45a), כאשר נשים לב ש- :

נציב נתונים ונקבל:

נוכל כעת לחשב את הטמפרטורה של הפן החיצוני של הלוח הקראמי:

נציב נתונים ונקבל:

שאלה 2

נתונים:

סעיף א’

סכמת הצינור.

לפי משוואה (IH8.45b):

נחשב את ההתנגדות הכוללת . מאחר ויש צינור דק דופן, הסעה פנימית, והסעה חיצונית:

חסר לנו למצוא מהו . מספר ריינולדס הרלוונטי הוא:

לכן, אנו בזרימה טורבולנטית. נבדוק האם אנו בזרימה מפותחת לפי אורך אזור התפתחות טורבולנטי:

לכן אנו בזרימה מפותחת, ועלינו להשתמש במשוואה (IH8.60):

נציב את שחישבנו וגם כי הזורם מתקרר לאורך הצינור:

נציב בביטוי לסך ההתנגדות:

לכן מקדם מעבר החום (בצורה המוזרה שהגדירו בפתרון הרשמי):

נציב בביטוי ל-:

לכן:

סעיף ב’

סכמת הצינורות.

מאחר וההספק קטן פי , מספר ריינולדס קטן פי :

לפיכך, משטר הזרימה שלנו השתנה והוא כעת למינרי. נבדוק האם הזרימה מפותחת לפי משוואה (IH8.23):

ולכן אנו בזרימה מפותחת. נסיק שעלינו להשתמש בקורלציה לזרימה למינרית מפותחת. מאחר ואין לנו לא טמפרטורה קבועה ולא שטף חום קבוע, נניח ממוצע בין שני המקרים, :

נציב בחזרה בביטוי ל- כדי לקבל שהפעם, עבור כל צינור:

מאחר ואנו כעת עובדים עם צינורות במקביל, סך ההתנגדות הכולל של כולם הוא:

כאשר נציב בחזרה בביטוי לטמפרטורה של המים ביציאה מהצינור, נקבל:

כלומר, הצלחנו לקרר את המים עד לטמפרטורת הסביבה. מעולה!

סעיף ג’

סכמת הצינורות הקצרים.

נשים לב שאנו עדיין בזרימה למינרית מפותחת. מאחר ואנו עובדים עם , הביטוי שלנו להתנגדות הכוללת על כל צינור הוא:

שזה פשוט פי מהביטוי שהיה לנו בסעיף ב’ עבור כל צינור. הכפלה פי זו מתקזזת עם העובדה שיש לנו צינורות, כך שההתנגדות של סך המערכת היא:

ונסיים עם הטמפרטורה:

באסה.

שאלה 3

סכמת הבעיה.

נתונים:

תכונות המים:

סעיף א’

בסביבתו המקומית של החיישן., בהינתן והטמפרטורה הממוצעת באמצע הצינור היא :

זרימה מקומית סביב החיישן.

נבדוק האם הזרימה טורבולנטית/למינרית בסוף הצינור:

ולכן הזרימה טורבולנטית. נשים לב כי הזרימה מפותחת:

מאחר והזרימה טורבולנטית, נשתמש במשוואה (IH7.54). נשים לב שעלינו להשתמש ב-:

נציב לתוך מקדם ההסעה (על החיישן) ונקבל:

סעיף ב’

לפי משוואה (IH8.40), עבור שטף חום קבוע:

הבעיה היא שאנו לא יודעים את . אבל, אנו כן יודעים למצוא את , כי אנו יודעים את מקדם ההסעה מהחיישן, ששפתו בטמפרטורה . לכן:

לפי משוואה (3.1), הטמפרטורה באמצע הצינור היא גם:

נשווה בין שתי המשוואות, ונמצא כי הטמפרטורה בכניסה:

נציב נתונים ונקבל:

מאחר ואנו מעוניינים בטמפרטורה ביציאה מהצינור, נציב ב-(3.1):

נציב נתונים ונקבל: