HTF1_006 זרימה פנימית

→ קודם: HTF1_005הבא: HTF1_007 ←

מבוא

נביט כעת בהסעות של זרימות פנימיות. נזכור שעבור זרימות חיצוניות, אין אילוצים גאומטריים על התפתחות שכבת גבול, לעומת זרימות פנימיות, בהן הזורם כלוא ע”י המרחב.

שיקולים הידרודינמיים

כאשר אנו דנים בזרימה חיצונית, אנו תמיד שואלים האם הזרימה למינרית או טורבולנטית. בזרימה פנימית, אנו חייבים גם להתייחס לשאלה האם הזרימה מפותחת?

תנאי הזרימה

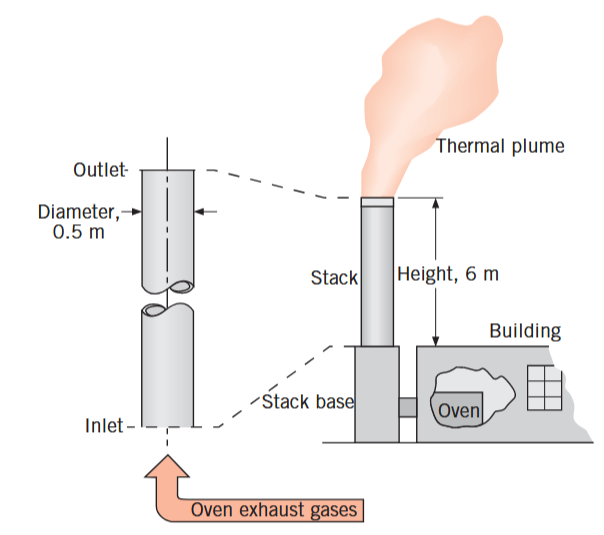
נביט בזרימה למינרית בצינור עגול ברדיוס , בו נכנס זורם במהירות אחידה.

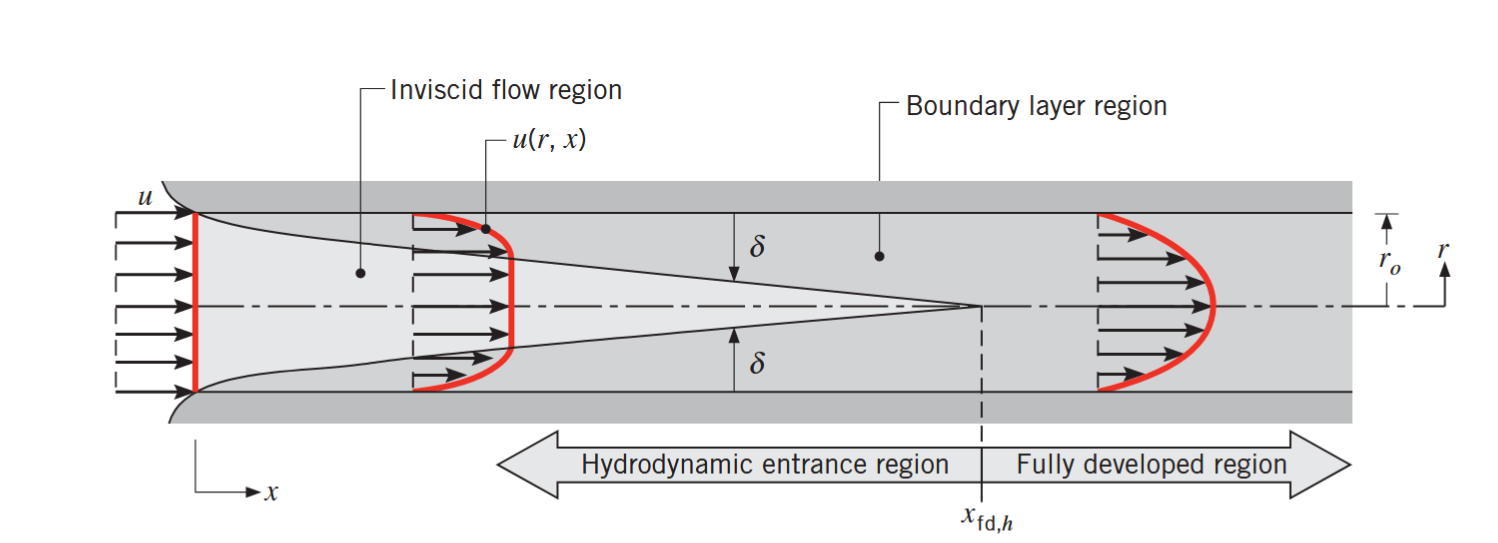
התפתחות שכבת גבול הידרודינמית למינרית בצינור עגול. (Bergman & Lavine, 2017).

אנו יודעים שכאשר הזורם בא במגע עם שפת הצינור הפנימית, ישנם השפעות צמיגות, ומתפתחת שכבת גבול בכיוון . התפתחות זו מתרחשת על חשבון צמצום אזור הזרימה הלא צמיגית ומסתכמת בהשתלבות שכבות הגבול באמצע הצינור. לאחר השתלבות זו, השפעות צמיגות דומיננטיות יותר לאורך כלל השטח חתך ופרופיל המהירות לא משתנה יותר עם גדילת . במקרה זה נאמר שהזרימה מפותחת, והמרחק מהכניסה בו מתרחשת תופעה זו נקרא אורך הכניסה ההידרודינמי, . כפי שמוצג באיור לעיל, פרופיל מהירות הזרימה המפותחת הוא פרבולי לזרימה למינרית בצינור עגול. לזרימה טורבולנטית, הפרופיל שטוח יותר כתוצאה מערבוב טורבולנטי בכיוון הרדיאלי.

כאשר אנו עוסקים בזרימה פנימית, נרצה תמיד לדעת מהו האורך הזה, והוא שונה עבור זרימה למינרית וטורבולנטית. מספר ריינולדס לזרימה בצינור עגול מוגדר כ:

כאשר הוא המהירות הממוצעת בשטח החתך ו- הוא קוטר הצינור. בזרימה מפותחת, מספר ריינולדס הקריטי הגורם לטורבולנציה הוא:

למרות שמספרי ריינולדס יותר גבוהים () נדרשים כדי לקבל טורבולנציה מלאה.

עבור זרימה למינרית, אורך הכניסה ההידרודינמי ניתן לביטוי:

עבור זרימה טורבולנטית:

בקורס זה אנו נניח שזרימה טורבולנטית היא מפותחת עבור .

מהירות ממוצעת

כיוון שהמהירות משתנה לאורך שטח החתך, עלינו לעבוד עם ממוצע משקולל של המהירות, , כאשר עוסקים בזרימה פנימית. מהירות זו מוגדרת כך שכאשר מוכפלת בצפיפות הזורם ושטח החתך , נקבל את קצב זרימת המסה בצינור - הספיקה:

לזרימה בלתי דחיסה בצינור עם שטח חתך אחיד, ו- בלתי תלויים ב-. לכן, עבור צינור עגול ():

ניתן גם לבטא את הספיקה כאינטגרציה על שטף המסה לאורך שטח החתך:

לכן, לזרימה בלתי דחיסה בצינור עגול:

מקדם חיכוך דרסי-ויסבך

בבעיות זרימה פנימית, מפל הלחצים הוא אחד מהגדלים הכי דומיננטיים בהשפעתם על הזרימה הפנימית. כמהנדסים, אנו מאוד מעוניינים בו כי הוא קובע למשל איזה סוג ואיזה חוזק של משאבה אנו צריכים. כדי לקבוע את מפל הלחצים, אנו נעזרים במה שנקרא:

הגדרה: מקדם חיכוך דרסי-ויסבך

מקדם חיכוך דרסי-ויסבך שהוא גודל חסר ממדי המוגדר כ:

אין לבלבל בין גודל זה למקדם חיכוך שמוגדר כ:

ניתן להראות שעבור זרימה למינרית מפותחת בצינור:

לזרימה טורבולנטית מפותחת, הניתוח הרבה יותר מסובך. מתוצאות אימפיריות מקבלים את המשוואה הסתומה, שתלויה גם בחספוס המשטח :

במקרה של צינור חלק, נוכל פשוט לחשב את מקדם החיכוך לזרימה טורבולנטית באופן הבא:

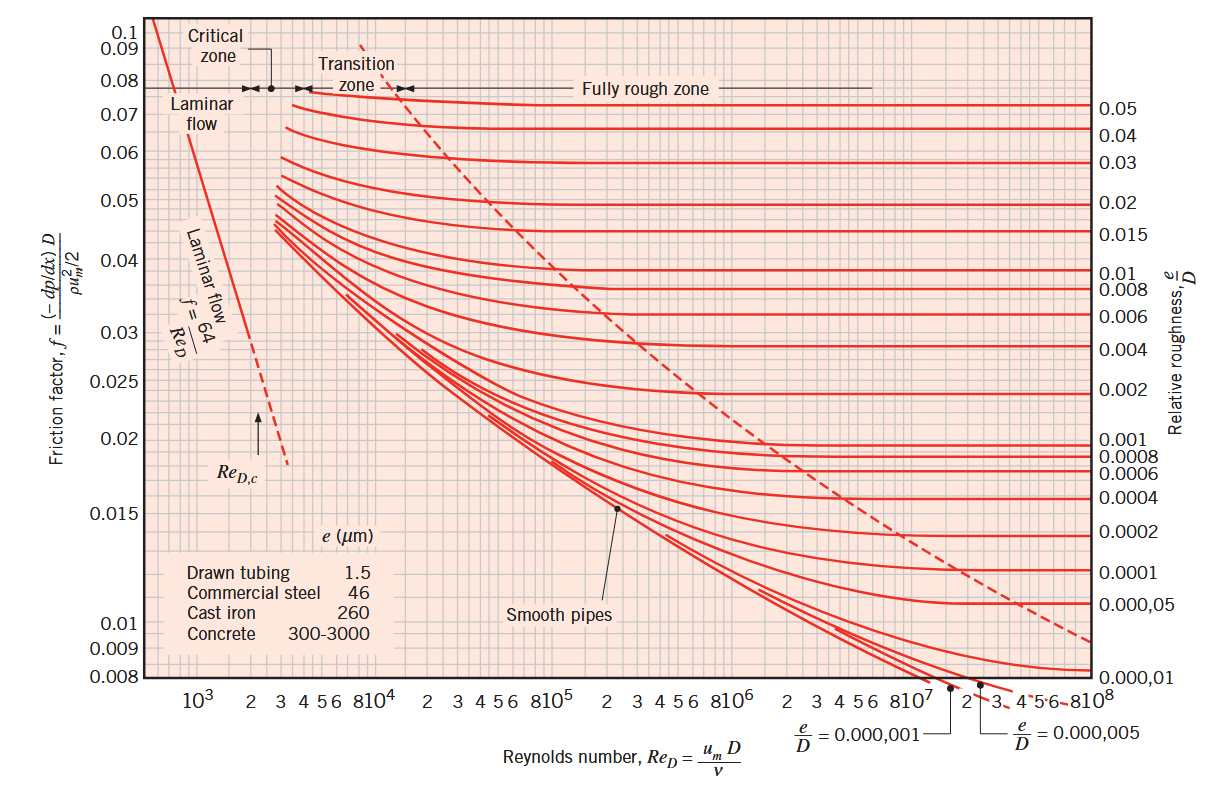
דיאגרמת מודי - מקדם חיכוך לזרימה מפותחת בצינור עגול.

כעת, אנו יכולים לחשב את את מפל הלחצים באופן הבא:

הספק המשאבה הדרוש כדי להתגבר על מפל לחצים זה יהיה:

עבור נוזל בלתי דחיס.

שיקולים תרמיים

נביט כעת בהיבטים התרמיים של הזורם. אם זורם נכנס לצינור כפי שמוצג באיור הבא, בטמפרטורה קבועה שיותר קטנה מטמפרטורת השפה, מעבר חום בהסעה מתרחש, ושכבת גבול תרמית מתחילה להתפתח.

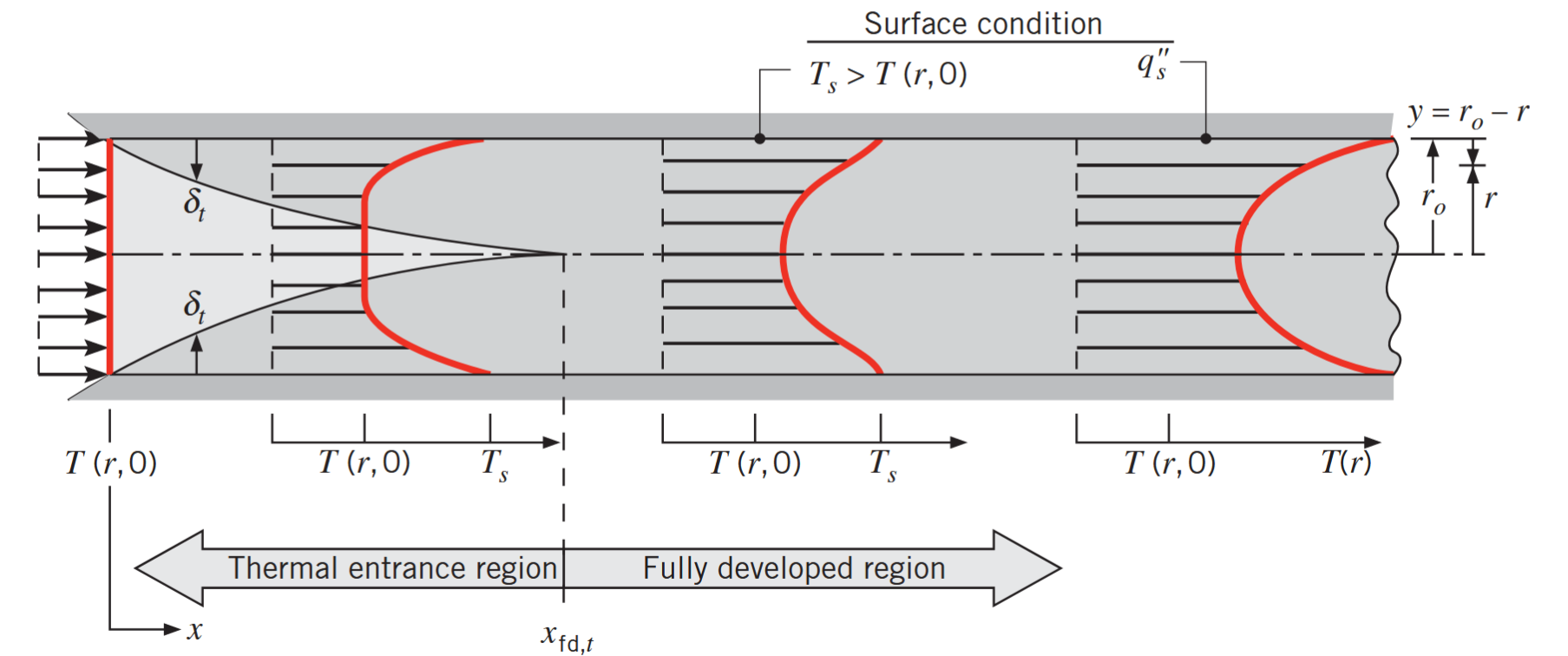
התפתחות שכבת גבול תרמית בצינור עגול עבור טמפרטורה קבועה, ושטף חום קבוע (בנפרד). (Bergman & Lavine, 2017).

בנוסף, אם תנאי השפה על שפת הצינור הפנימית הוא טמפרטורה קבועה ( קבוע), או שטף החום קבוע ( קבוע), נקבל זרימה מפותחת לאחר אורך התחלה מסוים.

אורך אזור ההתפתחות עבור זרימה למינרית הוא:

עבור זרימה טורבולנטית, התנאים על זרימה לרוב לא תלויים במספר פרנדטל, וכקירוב ראשוני, אנו נניח כי גם .

טמפרטורה ממוצעת

באותו אופן כמו מהירות ממוצעת, אנו מגדירים את הטמפרטורה הממוצעת באופן של ממוצע משוקלל:

בצורה אינטגרלית:

או:

עבור צינור עגול עם צפיפות וקיבול חום אחידים:

חוק הקירור של ניוטון

הטמפרטורה הממוצעת היא נקודת ייחוס נוחה לזרימות פנימיות, והיא מתפקדת כמו לזרימה חיצונית. באותו אופן, נוכל לרשום בעזרה את חוק הקירור של ניוטון:

כאשר הוא מקדם ההסעה ה-מקומי. אבל, ישנו הבדל חשוב בין ל-. בעוד קבוע בכיוון הזרימה, משתנה בכיוון זה.

מאזן אנרגיה בזרימה פנימית

כיוון שהזרימה בצינור סגורה לחלוטין, נוכל להשתמש מאזן האנרגיה כדי למצוא איך הטמפרטורה הממוצעת משתנה לאורך הצינור.

נביט למשל בזרימה בצינור באיור הבא:

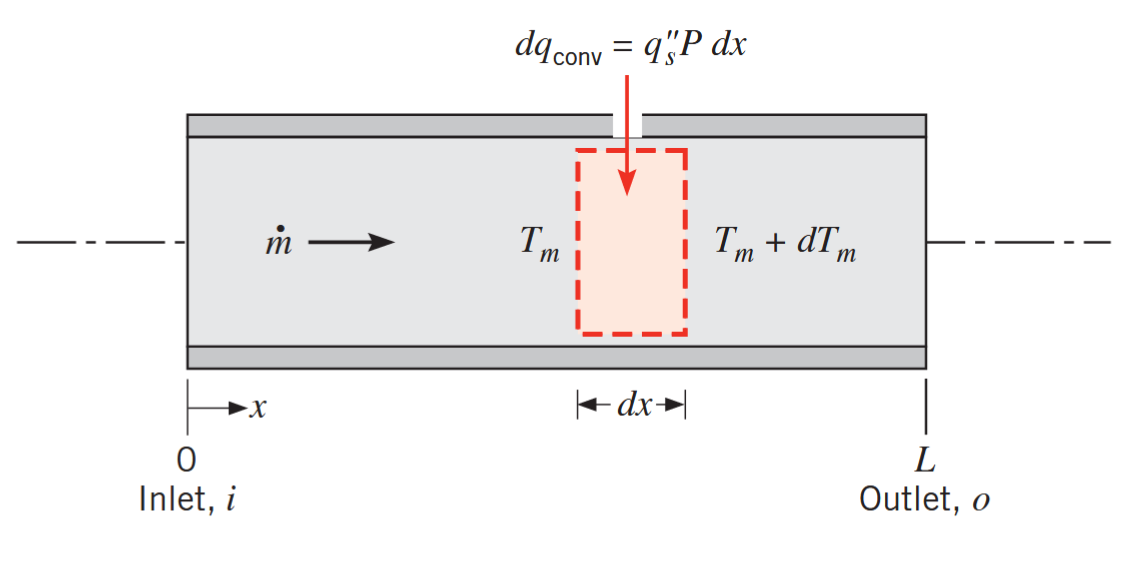
נפח בקרה לזרימה פנימית בצינור. (Bergman & Lavine, 2017).

זורם נע בספיקה קבועה , ומעבר החום בהסעה מתרחש בפנים הצינור. בהנחה והדיסיפיביות של הזורם זניחה, ומדובר בנוזל בלתי דחיס, או גז אידיאלי בלחץ די קבוע, ונזניח סך מעבר חום כללי בהולכה בכיוון הצינור, נקבל מחוק הראשון של התרמודינמיקה:

לאורך צינור סופי.
אם ניישם את החוק הראשון לנפח בקרה לעיל, כאשר נזכור ש- מתאר אינטגרציה על קצב מעבר החום באדוקציה לאורך שטח החתך, נקבל:

או:

את קצב מעבר החום הדיפרנציאלי נוכל גם לרשום כ- , כאשר הוא היקף השפה ( לצינור עגול). נקבל ש:

משוואה זו מאוד שימושית, כי ממנה אנו יודעים למצוא את עבור כלשהו. הפתרון שלה תלוי בתנאי השפה, ונעסוק בעיקר בתנאי שפה של טמפרטורה קבועה על דופן הצינור ושטף חום קבוע דרך דופן הצינור.

במקרה של שטף חום קבוע, מאחר ו- לא תלוי ב-, נוכל לומר ש:

בנוסף, אנו גם יודעים לומר ממשוואה (IH8.37) ש:

מאינטגרציה על משוואה זו לפי :

עבור טמפרטורה קבועה, נקבל פתרון שונה לגמרי. נסמן , ואז משוואה (IH8.37) הופכת להיות:

זוהי משוואה פרידה, שנפתור באינטגרציה:

מהגדרת מקדם הסעה ממוצע, כאשר קבוע, נסיק כי:

כאשר הוא מקדם ההסעה הממוצע מתחילת הצינור עד נקודה . נסדר מחדש ונקבל:

כדי למצוא את מעבר החום הכולל, אנו יודעים ש:

מהצבת (IH8.41a) נקבל:

כאשר הוא שטח פנים הצינור () ו- הוא הממוצע הלוגריתמי של הפרש הטמפרטורות:

משוואה (IH8.43) היא צורה של חוק הקירור של ניוטון לכל הצינור, ו- הוא הפרש הטמפרטורות הממוצע המתאים לאורך הצינור. הסיבה שיש לנו שם לוגריתם היא שהטמפרטורה משתנה אקספוננציאלית.

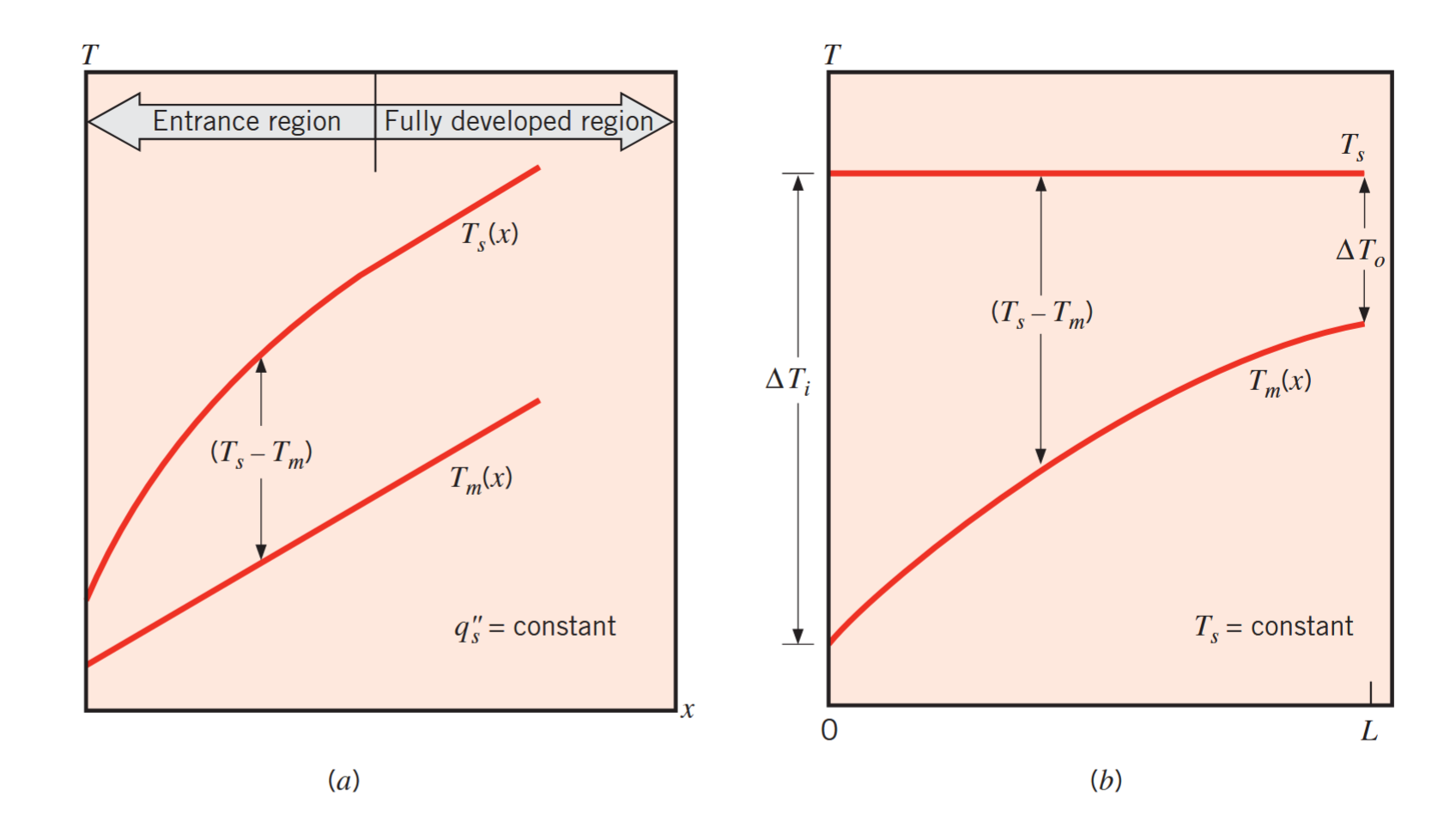
טמפרטורה ממוצעת כתלות ב- למעבר חום בצינור. (a) שטף חום קבוע. (b) טמפרטורת שפה קבועה. (Bergman & Lavine, 2017).

חשוב גם לשים לב שברוב המקרים הטמפרטורה של נוזל חיצוני היא זו שקבועה, בעוד טמפרטורת השפה נתונה לשינוי.

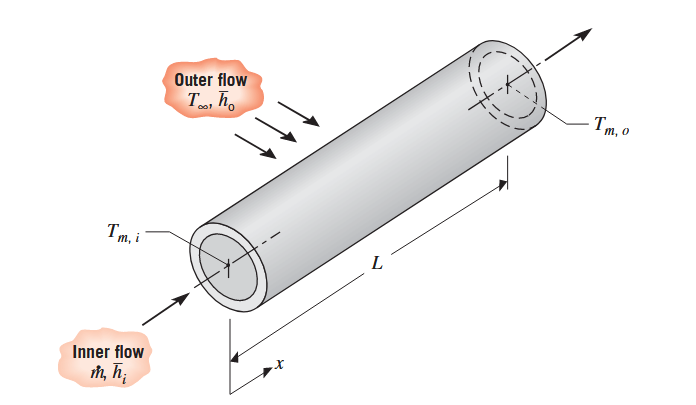
מעבר חום בין זורם הזורם סביב צינור וזורם הזורם דרכו. (Bergman & Lavine, 2017).

במקרים כאלו, נוכל עדיין להשתמש בתוצאות שקיבלנו, כאשר נציב את (טמפרטורת הזורם החיצוני) במקום , ונציב את (מקדם המעבר חום הכללי הממוצע) במקום . כלומר:

וגם:

מקדם מעבר החום הכללי במקרה שלנו יכלול את ההסעה בפנים וחוץ הצינור. לצינור עבה דופן עם הולכה תרמית נמוכה, נצטרך גם להתחשב בהשפעה של ההולכה דרך הקיר. נשים לב שהמכפלה מניבה את אותה התוצאה, ללא תלות אם היא הוגדרה עבור שטח הפנים של הדופן הפנימית () או החיצונית . נשים לב גם ש- שקולה לסך ההתנגדות התרמית בין הזורמים, שממשוואה (IH8.45a) ו-(IH8.46a) ניתנים לביטוי כ:

וגם:

הערה:

במידה ונתון לנו טמפרטורה חיצונית אחידה, , במקום טמפרטורה של זורם חיצוני , נוכל פשוט להחליף את ב- במשוואות לעיל, כאשר ב- נתייחס רק להתנגדות להסעה הפנימית וההתנגדות להולכה בין המשטח הפנימי למשטח החיצוני של הצינור. זהו המצב לרוב בבעיות של מעבר פאזה על דופן הצינור.

זרימה למינרית בצינור עגול

כדי להשתמש בתוצאות שקיבלנו מקודם, עלינו לדעת מהו מקדם ההסעה . כדי למצוא זאת קודם עלינו להבין אם מדובר בזרימה מפותחת, והאם הזרימה למינרית או טורבולנטית.

זרימה מפותחת למינרית

עבור המקרה הלמינרי, , ובשטף חום קבוע , נקבל את הקורלציה:

כלומר, מספר נוסלט קבוע - לא תלוי ב- או , או במיקום .
אם הטמפרטורה קבועה, מקבלים גם מספר נוסלט קבוע:

זרימה למינרית באזור הכניסה

התוצאות הקודמות תקפות רק אם גם פרופיל הטמפרטורות וגם פרופיל המהירות הגיעו לאזור המפותח. אם אחד מהם לא מפותח, נאמר שאנו באזור ההתפתחות, או אזור הכניסה (entry region). נשים לב שכל עוד המהירות לא מפותחת, הזרימה התרמית לא יכולה להיות מפותחת. נאמר שאזור הכניסה משולב (combined entry length) אם גם המהירות וגם הזרימה התרמית לא מפותחים, ושאזור הכניסה תרמי (thermal entry length) אם רק הזרימה התרמית עוד לא מפותחת.
פתרונות לשני אזורי הכניסה פותחו, וחלקם מוצגים באיור הבא:

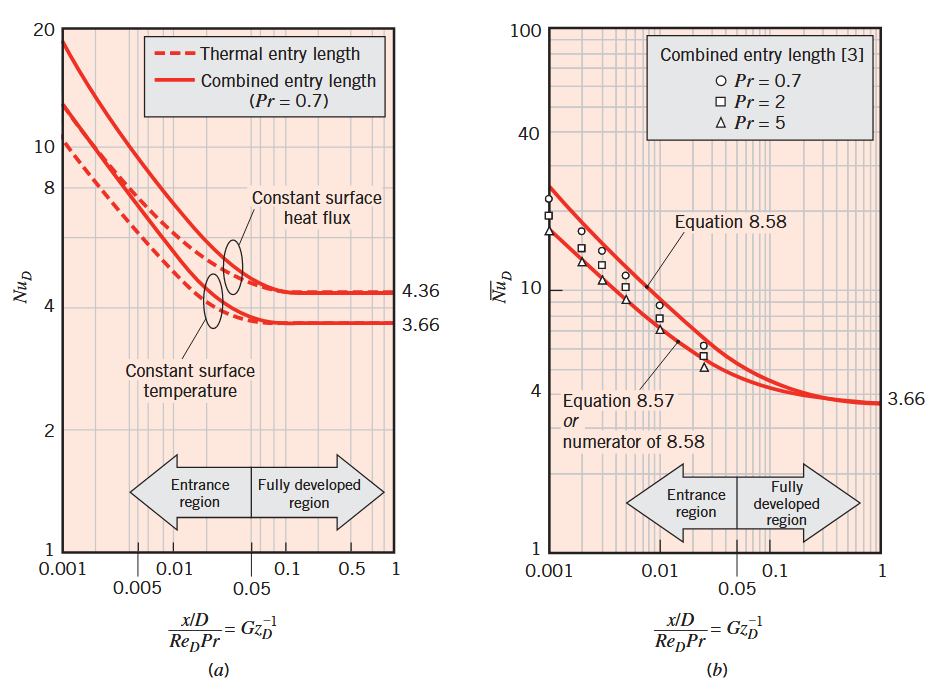
תוצאות מאזורי כניסה לזרימה למינרית בצינור עגול עם טמפרטורות שפה קבועות. (a) מספרי נוסלט מקומיים. (b) מספרי נוסלט ממוצעים. (Bergman & Lavine, 2017).

עבור אזור ההתפתחות, נהוג להגדיר עוד מספר כיפי:

הגדרה: מספר גרייטז

מספר גרייטז (Graetz) מוגדר כ:

מבחינת מספרית, עבור אזור כניסה תרמית:

כאשר קבוע. קורלציה זו נכונה גם עבור אזור כניסה משולב במידה ו-.

בכללי, לבעיית אזור כניסה משולב:

כאשר קבוע, ו- .

זרימה טורבולנטית בצינור עגול

כיוון שהניתוח של זרימה טורבולנטית יותר מסובך מזרימה למינרית, אנו נאלצים לחזור לתוצאות אמפיריות.

זרימה מפותחת טורבולנטית

לזרימה מפותחת (תרמית והידרודינמית), הזרימה הטורבולנטית בצינור עגול, מספר נוסלט המקומי הוא:

כאשר לחימום () ו- לקירור . נמצא כי משוואות אלו נכונות לתנאים:

נוכל להשתמש במשוואה אלו עבור הפרשי טמפרטורות די נמוכים, כאשר תכונות הזורם מחושבות עבור .

לזרימות המאופיינות בהפרשי טמפרטורות יותר קיצוניים, ולפיכך בתכונות זורם יותר נתונות לשינוי, עדיף להשתמש בקורלציה הבאה:

כאשר כל התכונות, חוץ מ-, מחושבות עבור . ניתן להשתמש בקורלציות אלו בקירוב יחסית טוב גם לתנאי שפה של טמפרטורה קבועה וגם לשטף חום קבוע.

למרות שהמשוואות לעיל די טובות, עדיין ניתן לקבל שגיאות של עד בתנאים מציאותיים. ניתן להקטין את השגיאות ל- ע”י שימוש בקורלציה טיפה יותר עדכנית. עבור זרימה פנימית בצינור חלק בטווח מספרי ריינולדס די גדול, נוכל לומר ש:

כאשר מקדם החיכוך נמצא ממשוואה (IH8.21). קורלציה זו מתאימה ל- ו- , והתכונות מחושבות עבור .

דוגמה: בעיה 8.48 בספר

ארובה של מפעל חשופה לזרימת אוויר בטמפרטורה ומהירות . קוטר הארובה הוא וגובהה . ספיקת הגז היא , וטמפרטורת הכניסה היא .

ראשית, נצטרך להעריך את תכונות הזורם. נבחר טמפרטורה ביציאה של בתור ניחוש ראשוני. עבור הזרימה בצינור נשתמש באוויר בטמפרטורה :

עבור הדופן החיצונית נניח טמפרטורה של . לכן נחשב תכונות זורם עבור :

נפרק לפנים וחוץ הצינור.

• בתוך הצינור:

  ולכן אנו בזרימה טורבולנטית. לפי (IH8.60):

• מחוץ לצינור:

  לפי משוואה (IH7.54):

  ולכן:

  במקרה הזה טמפרטורת הדופן איננה קבועה - יש לנו זורם חיצוני על צינור דק דופן. לכן, לפי משוואה (IH8.45a), כאשר נשים לב ש- :

  המקדם מעבר חום הכללי במקרה שלנו הוא:

  נציב נתונים בביטוי ל-:

  שזה די קרוב לניחוש .
  נצטרך גם לוודא שהניחוש על טמפרטורת היציאה שלנו נכון. אם נבצע חוק ראשון זריז על דופן הצינור, נקבל:

  נציב נתונים ונקבל:

  שזה די קרוב ל- .

זרימה פנימית בצינורות לא עגולים

ישנם לא מעט מקרים בהם נצטרך לעבור עם צינורות לא עגולים. במקרים אלו, אנו מבצעים תיקון למספרי ריינולדס ונוסלט לפי הקוטר האפקטיבי/הידראולי:

כאשר הוא שטח החתך דרכו עובר הזרם, ו- הוא ההיקף של שטח חתך זה.
לזרימה טורבולנטית, שעדיין מתרחשת ב- , עדיין מומלץ להשתמש בקורלציות בזרימה טורבולנטית בצינור עגול עבור . אבל, בצינור לא עגול מקדמי ההסעה עלולים להשתנות ליד היקף השטח חתך, והם אפילו שואפים לאפס בדפנות. לכן, כאשר אנו משתמשים בקורלציה לצינור עגול, אנו מניחים שהמקדם הוא ממוצע לאורך ההיקף.

לזרימה למינרית, כבר לא נוכל להשתמש בקורלציות לצינור עגול, ובמקרים אלו פשוט נשלוף את המספרים מטבלה 8.1.

זרימה בצינורות טבעתיים

הרבה מבעיות הזרימה הפנימית עוסקות בזרימה של צינור בתוך צינור, מה שאומר ששטח החתך של הצינור החיצוני הוא טבעתי.

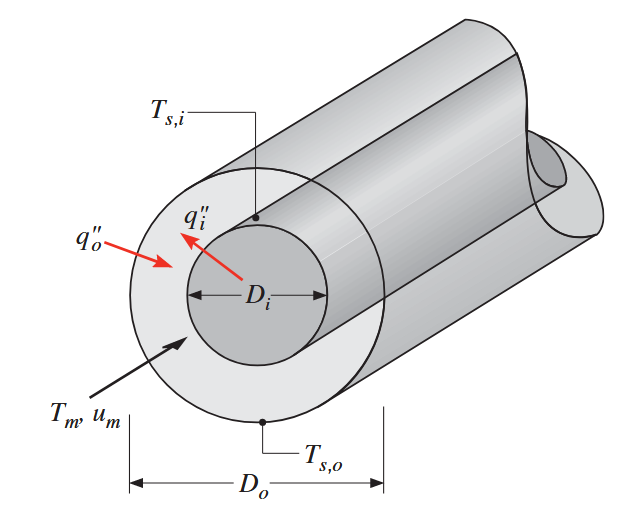
צינור טבעתי ממרוכז. (Bergman & Lavine, 2017).

נשים לב שלכל אחד מהצינורות יש מקדמי הסעה שונים, שמספר נוסלט המתאים להם הוא:

כאשר, ממשוואה (IH8.66), הקוטר האפקטיבי הוא:

למקרה של זרימה מפותחת עם משטח אחד מבודד והשני בטמפרטורה קבועה, ניתן למצוא את או מטבלה 8.2. כמובן שבמקרה זה יעניין אותנו רק המקדם הסעה מהמשטח האיזותרמי. במקרה של שטף חום אחיד בשני המשטחים, מספר נוסלט מחושב לפי:

כאשר את המקדמים ניתן למצוא מטבלה 8.3.

→ קודם: HTF1_005הבא: HTF1_007 ←