התנהגות מג”ש בהגברים גבוהים
יהי
אם למשל
אם
אם
כאשר נבחן את המקרים של פאזה מינימלית עם עודף קטבים של אחד או אפס, נקבל שתמיד נוכל לבקר בהגברים גבוהים.
לסיכום:
מערכות בהן הגברים גבוהים במשוב ניתנים ליישום הם:
- פאזה מינימלית ו-
- פאזה מינימלית ו-
- פאזה מינימלית ו-
ביצועי מצב מתמיד למערכות בחוג סגור
יהי
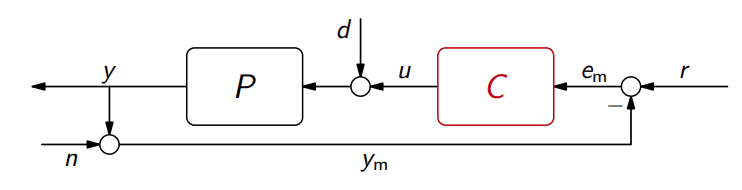
במבוא למשוב הצגנו את הפונקציות תמסורת השונות במשוב יחידה, ומהן נסיק כי:
נפרק ל-
-
במקרה ו-
𝟙 בהנחה והמערכת יציבה פנימית.
נרצה לדעת מתי
נשים לב שתנאי זה הוא רק על -
במקרה ו-
𝟙 כעת מתקיים
-
במקרה ו-
כעת מתקיים
איפוס שגיאה במנועי DC
למנוע DC תהליך מהצורה:

נחקור מתי השגיאה במצב מתמיד
שגיאה עבור אות ייחוס מדרגה
השגיאה עבור
במקרה זה לתהליך יש קוטב בראשית (אינטגרטור), כך שההגבר הסטטי שלו הוא
בהינתן ו-
נסיק ש-
שגיאה עבור הפרעת מדרגה
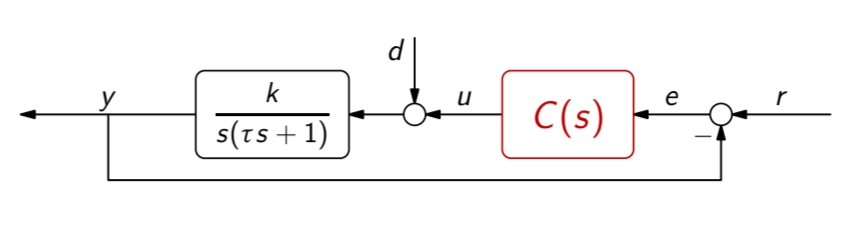
במקרה של
כאשר
כדי ש-
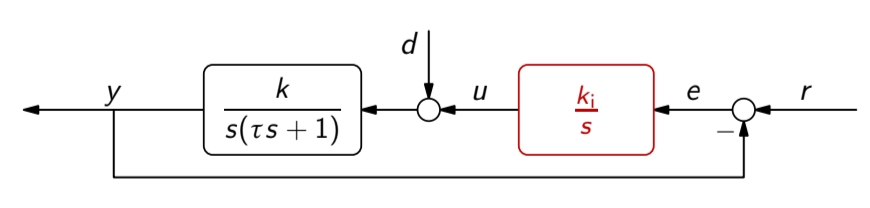
האות בקרה
נקרא בקר אינטגרלי (integral controller), או בקר I. הבקר הלא יציב
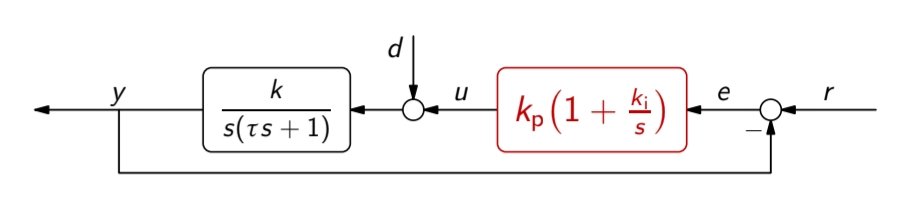
נביט במג”ש של המערכת:.
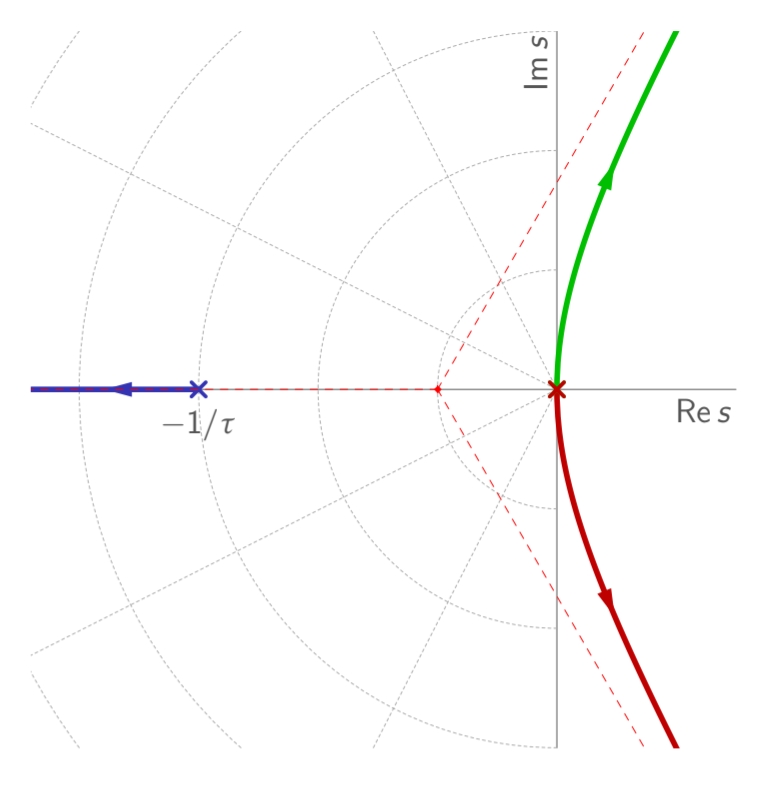
מג”ש של המערכת הנתונה. (Leonid Mirkin’s Homepage, n.d.).
נשים לב שתמיד יש ענף ב-RHP, ולכן הבקר לא יהיה יציב עבור אף הגבר
נציע בקר מסוג אחר:
ואז האות בקרה הוא מהצורה:
ולבקר זה קוראים בקר פרופורציונלי-אינטגרלי (proportional-integral controller), או פשוט בקר PI. גם בקר זה מקיים ש-
המג”ש שלו עבור ערכי
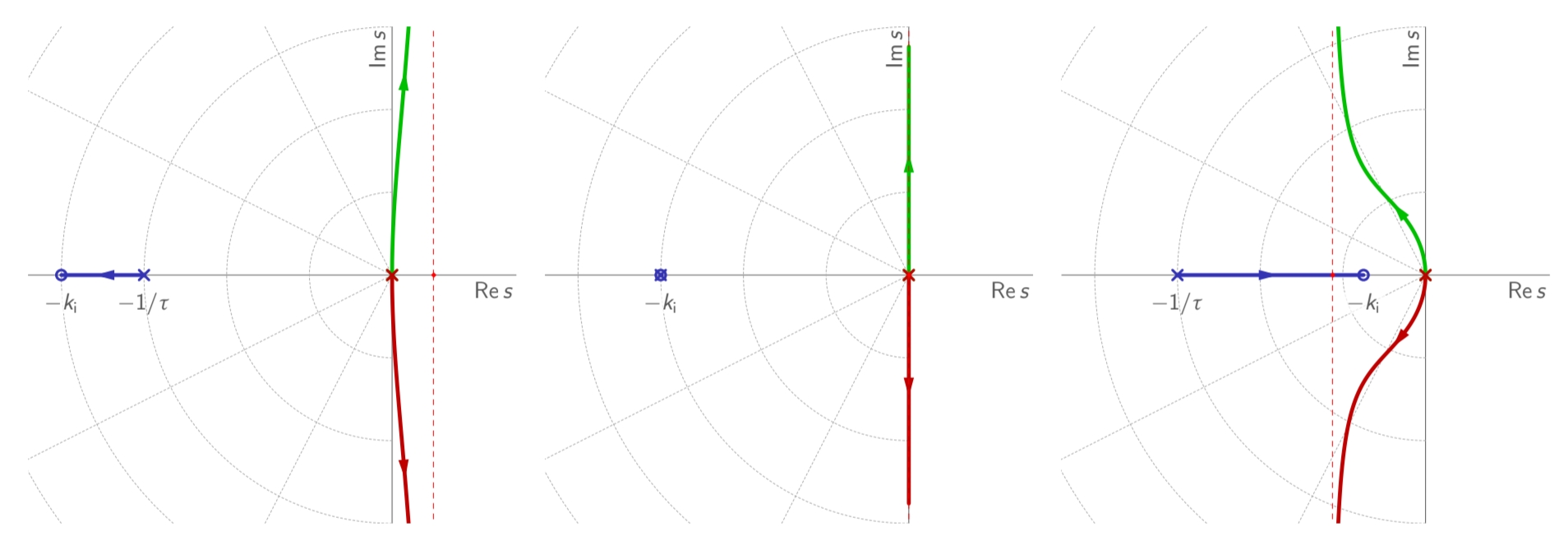
מה שמראה לנו שניתן לייצב את המערכת אמ”ם מרכז הכובד בצד השלילי של הציר הממשי, כלומר אם
שגיאה עבור אות ייחוס ריצה
במידה ויש לנו
לכן, ככל ש-
שגיאה עבור הפרעת ריצה
אם
אז, אם
ו-
שגיאה עבור אות ייחוס או הפרעה מחזורית
במקרה של
נקבל
שגיאה עבור רעש מדידה מחזורי
במקרה של
אז
תרגילים
תרגיל 1
נביט בדיאגרמת מג”ש הבאה:
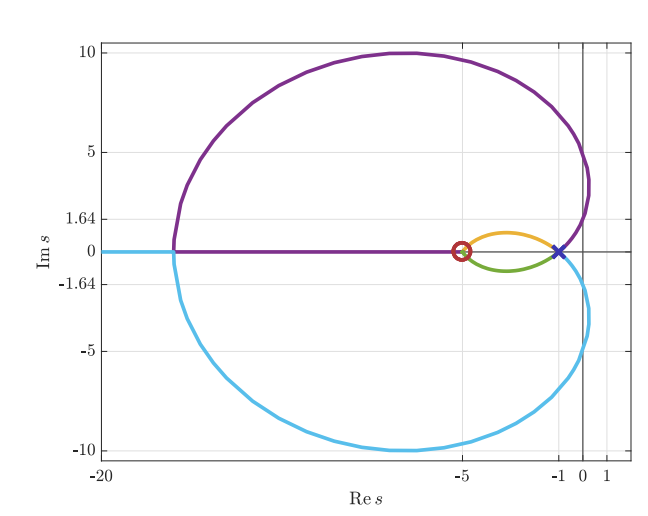
דיאגרמת מג”ש. (Leonid Mirkin’s Homepage, n.d.).
האיור לעיל מתאר את המג”ש של תהליך
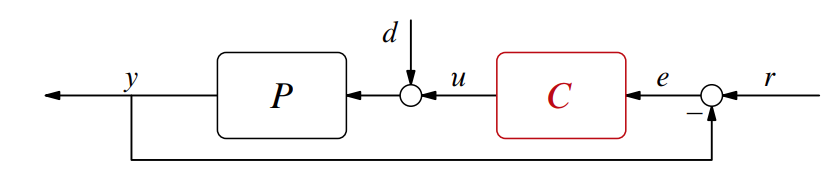
סעיף א’
האם ניתן לקבוע את
פתרון:
ניתן לראות 4 ענפים יוצאים מ-
נסיק שהתהליך
הערך
סעיף ב’
בהנחה והמקדמים של המונה של
פתרון:
הצורה של הענפים על הציר הממשי היא זהה לזו של
קיים ענף על הציר הממשי רק כאשר מימינו מספר אי זוגי של קטבים ואפסים.
נסתכל כאשר
לכן על הציר מרוכב יהיו ענפים במקומות שהם יש מספר אי-זוגי של קטבים ואפסים בצד ימין:
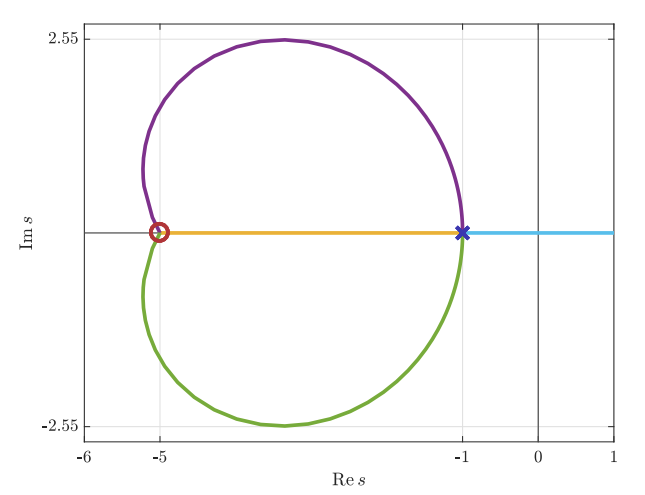
מג”ש עבור
.
סעיף ג’
האיור הבא מתאר תגובת מדרגה של החוג הסגור עבור
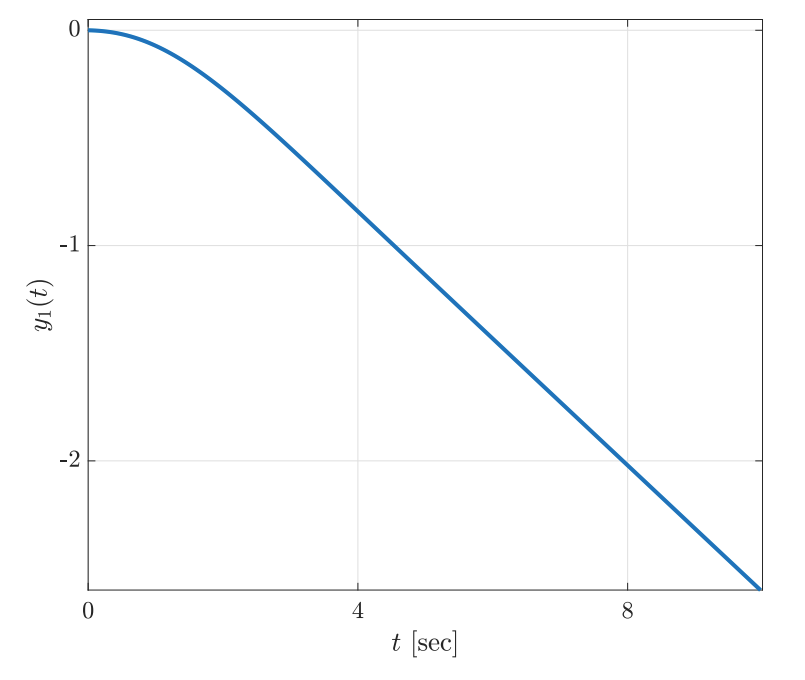
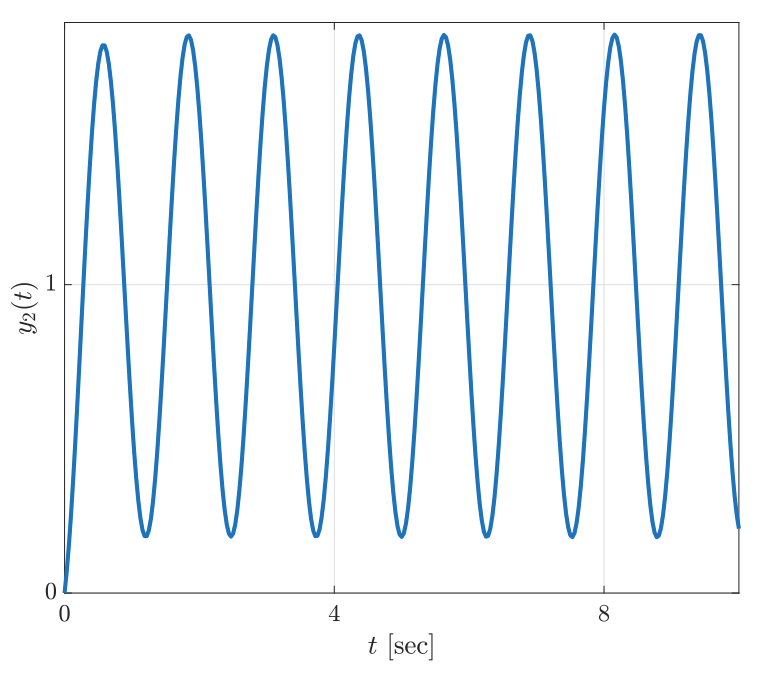
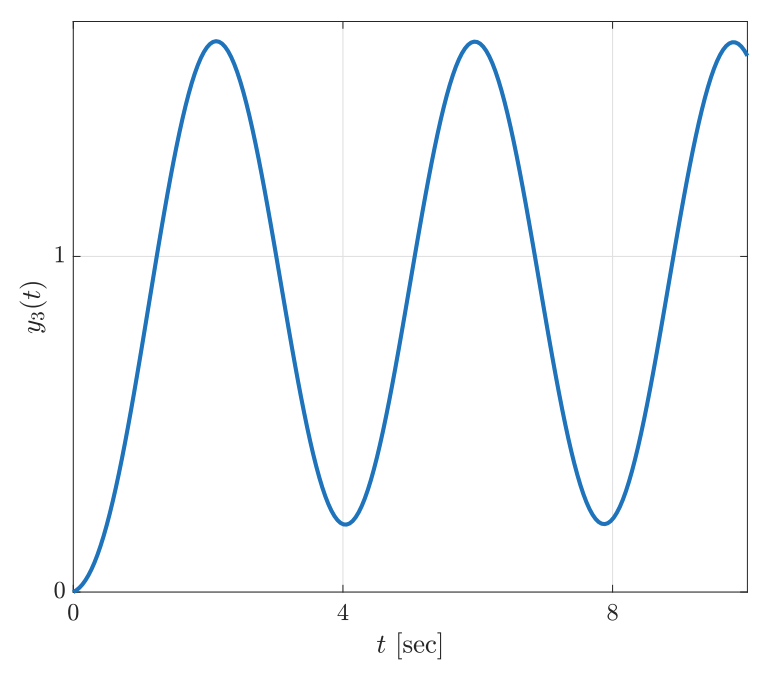
תגובות מדרגה של החוג הסגור עבור ערכי
שונים. (Leonid Mirkin’s Homepage, n.d.).
פתרון:
נשים לב שהגרף הראשון מתדבר, מה שמעיד על מערכת לא יציבה. שני הגרפים האחרים לא מתבדרים ולא מתכנסים, כך שהקטבים שלהם נמצאים על הציר המדומה.
בדיאגרמת מג”ש הנתונה, ישנם שני ערכי
משיטת האלימינציה, נותר לנו רק :
יכולנו גם לראות זאת מהתוצאה בסעיף ב’, שרק עבור
תרגיל 2
הביטו במערכת הבאה:
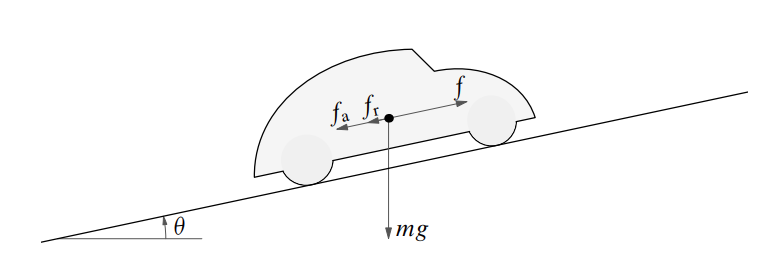
המערכת הנתונה על הרכב. (Leonid Mirkin’s Homepage, n.d.).
הבעיה כאן היא לשמור על מהירות יציבה
כאשר
כאשר
הניחו שהמערכת מבוקרת ע”י משוב יחידה, עם בקר PI:
עבור פרמטרים כלשהם
סעיף א’
שרטטו את המג”ש של המערכת ביחס להגבר הפרופורציוני
פתרון:
הייצוג מג”ש של המערכת במקרה זה:
יש לו שני קטבים ממשיים ב-
נפרק לשני מקרים:
- אם
משמאל ל-
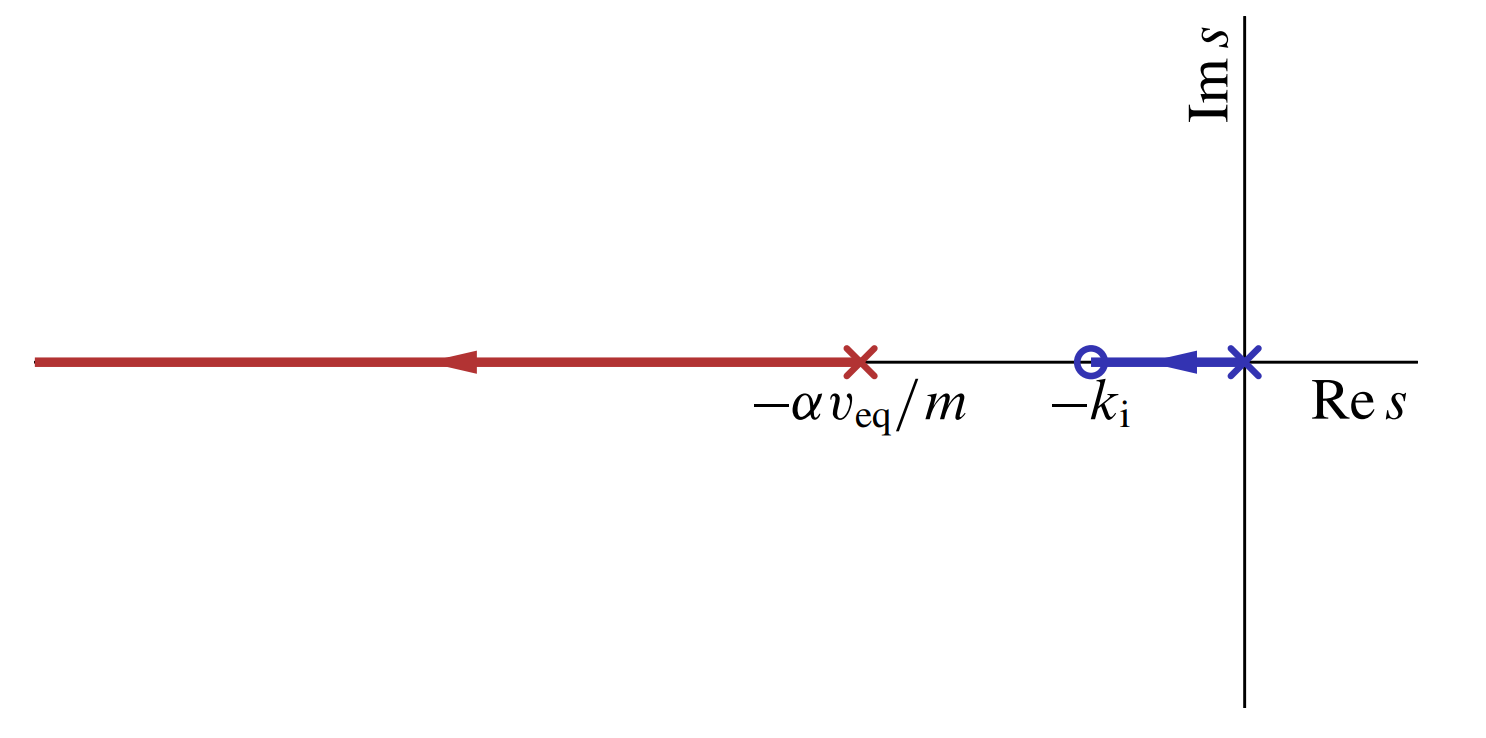
מג”ש עבור
- אם
משמאל ל-
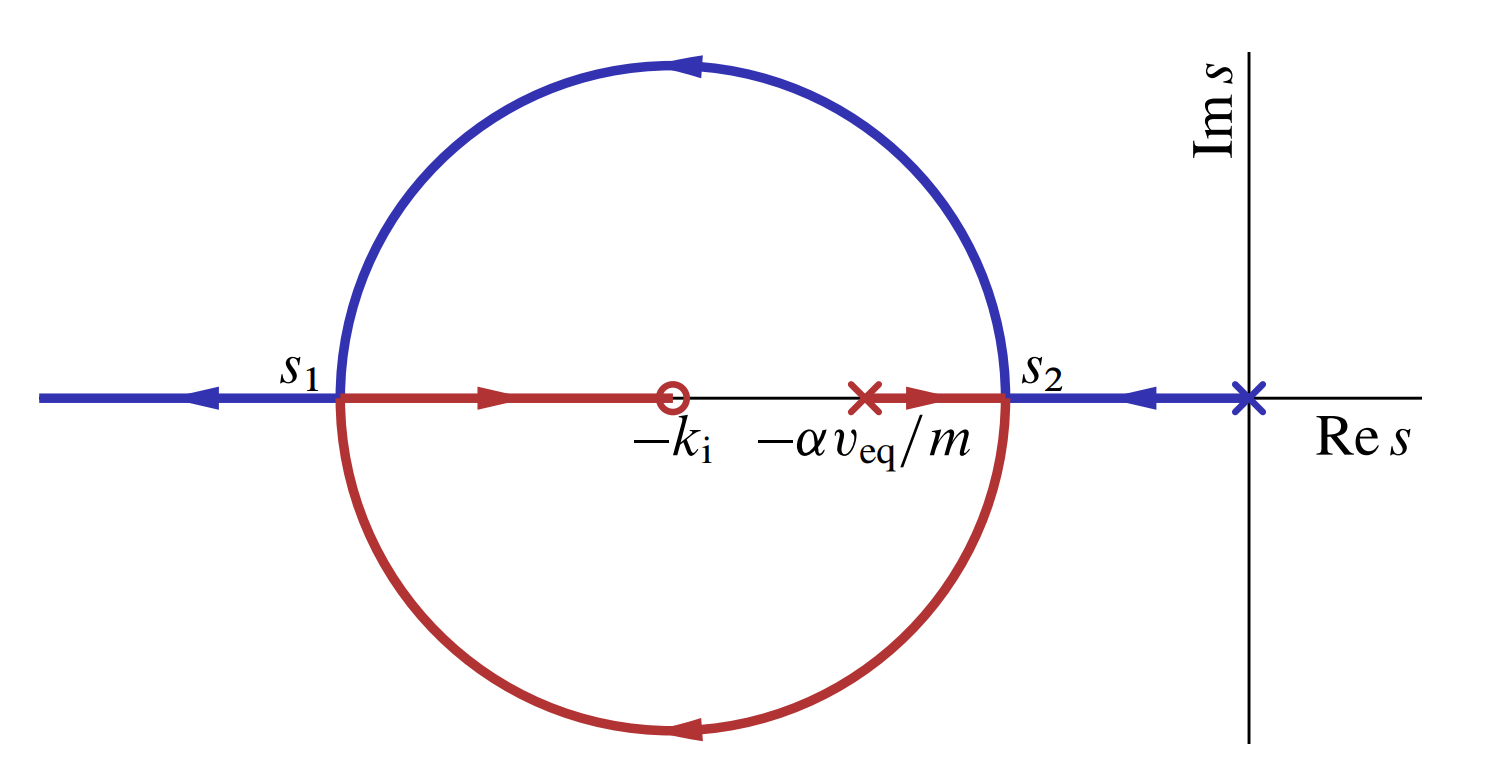
מג”ש עבור
- אם
כאשר
סעיף ב’
נתון:
שהוא מהצורה:
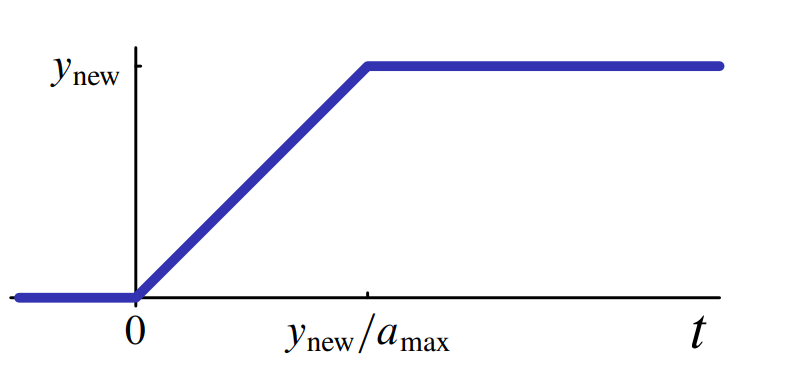
עבור תאוצה מקסימלית
מהי המהירות במצב מתמיד עבור
פתרון:
מאחר ויש לנו אינטגרטור בבקר, השגיאה מתאפסת לכניסה מדרגה באות ייחוס וגם למדרגה. לכן השגיאה במצב מתמיד היא אפס:
סעיף ג’
איך הבחירות של
פתרון:
היציבות של המערכת בחוג סגור לא תלויה ב-
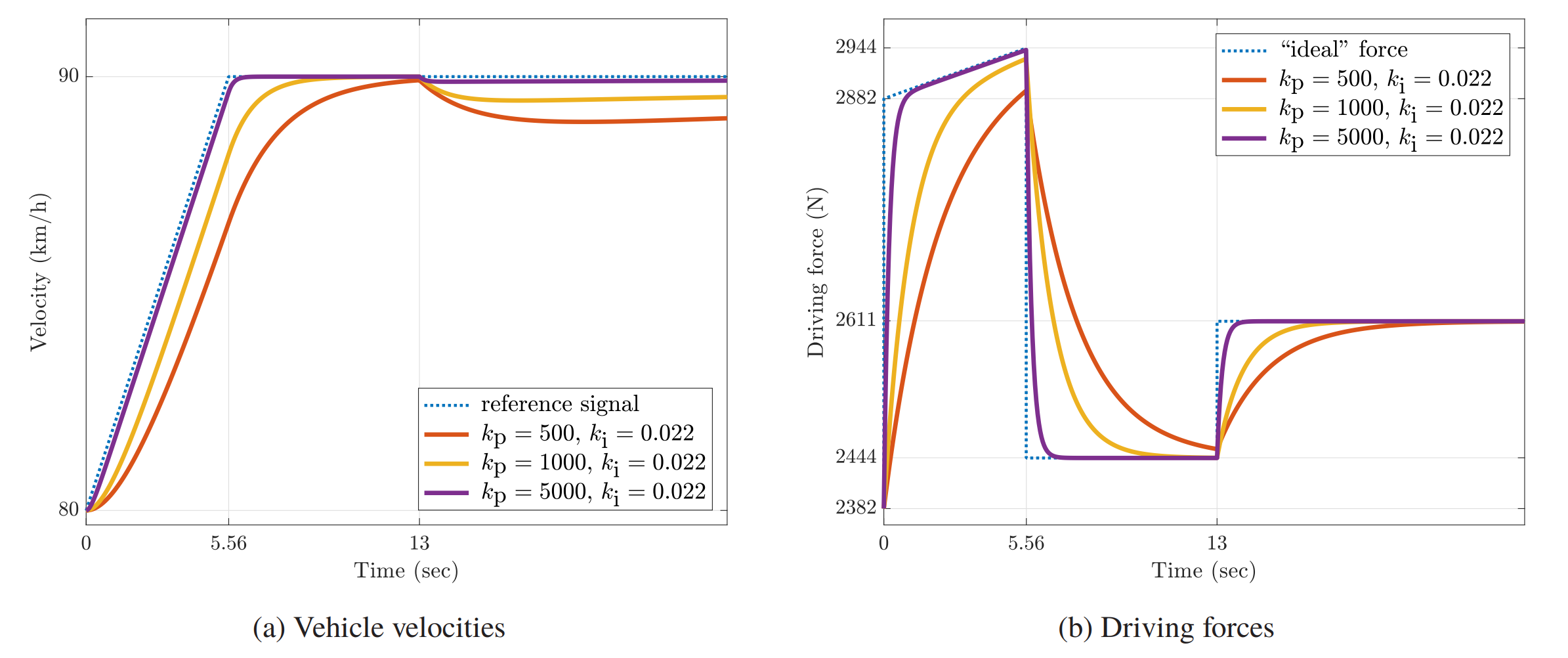
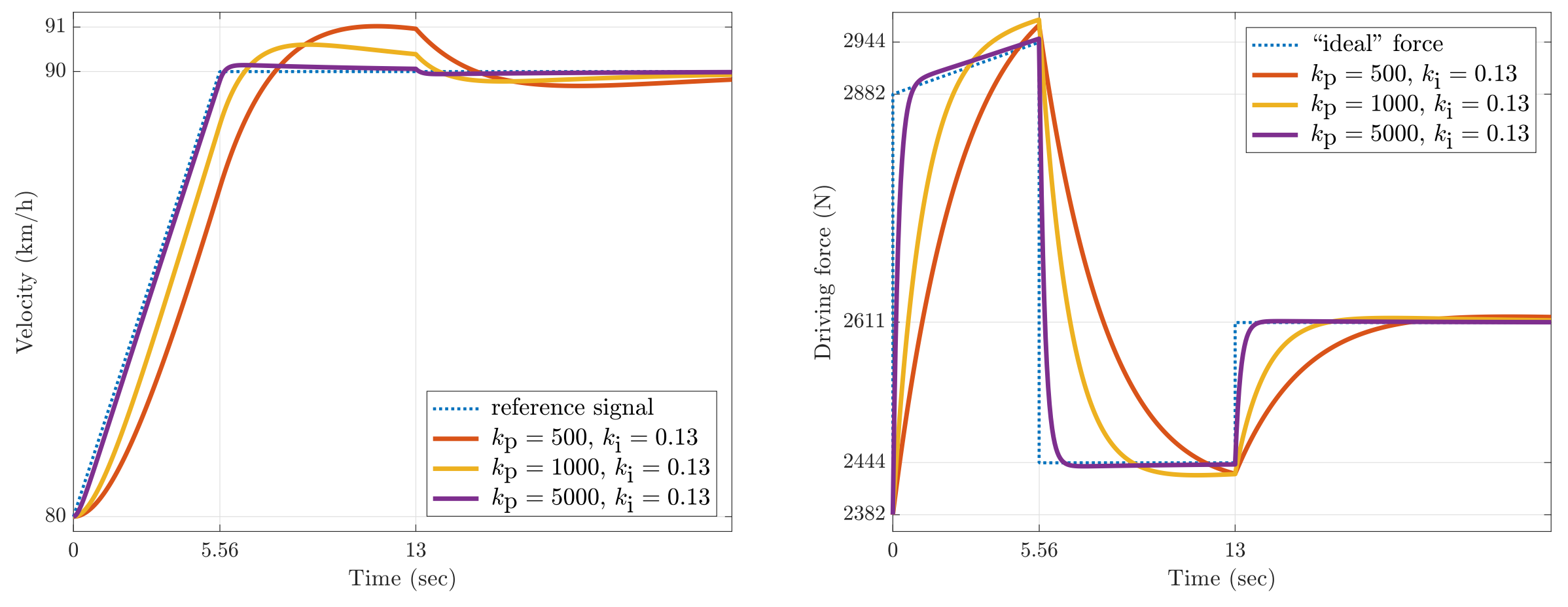
תגובות מהירות ל-
תחת שינויי שיפוע המסלול. הכוח ה”אידיאלי” הוא הכוח עבורו . נשים לב שעבור אנו מצמצמים קוטב של התהליך ע”י אפס של הבקר.
בכל מקרה, השגיאה במצב מתמיד מתאפסת, וככל שערך
