ICT1_008 עיצוב חוג

→ קודם: ICT1_007הבא: ICT1_009 ←

מבוא

בפרק קודם ראינו כיצד אנו מאפסים את אות השגיאה במצב מתמיד עבור אותות ייחוס והפרעות שונות. אבל מה אם אנו לא חייבים ש- , או מה אם ל- או- יש ספקטרום רחב של תדירויות והגבר גבוה במצב מתמיד לא ישים?

ביצועים במצב מתמיד

מעקב אחר אות ייחוס

נביט במערכת הבאה:

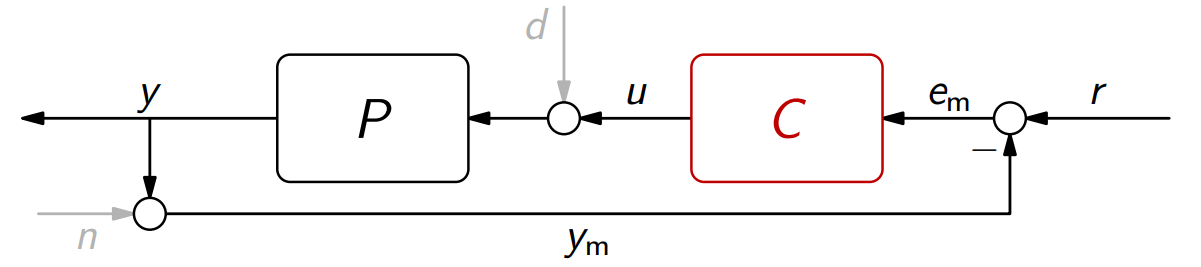
נסמן ב- את טווח התדירויות עבורו הספקטרום של מרוכז. כדי לקבל מעקב אחר אות ייחוס טוב, צריך להתקיים:

כאשר ו- הן התמרות לפלס של ו- בהתאמה.
לכן פונקציית הרגישות מקיימת:

כאשר נזכור ש- אם .

נסמן את פונקציית התמסורת של החוג הסגור כ- . לכן:

ולכן, לפי אי שוויון המשולש:

אנו רוצים להבטיח ש- יהיה קטן מחסם כלשהו . לכן, לפי הקשר לעיל, אם:

אז

לכל .
בגדול, כדי לקבל מעקב אחר אות ייחוס במצב מתמיד טוב, נדרוש ש- , יענו הגבר גבוה בחוג, בטווח התדירויות .

הפחתת הפרעות

באותו אופן, כאשר נתמקד בהפרעה:

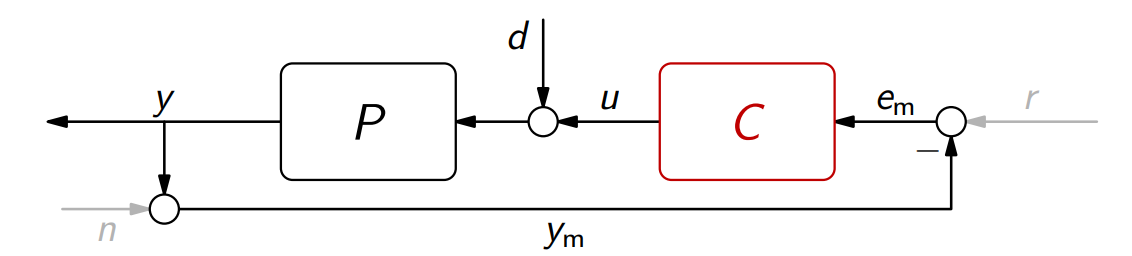
נסמן ב- את טווח התדירויות בו מרוכז. כדי לקבל הפחתת הפרעות טובה במצב מתמיד, אנו מבינים שצריך להתקיים:

כאשר ו- הן התמרות לפלס של ו- בהתאמה.
לכן, פונקציית הרגישות להפרעה צריכה לקיים:

כאשר נזכור ש- אם .
כעת, באותו אופן כמו במקרה הקודם, נשים לב שנצטרך הפעם לדרוש:

ואז נקבל ש:

לכל .
שוב, , כדי לקבל הפחתת הפרעות במצב מתמיד טובה, הגבר גבוה בחוג, בטווח התדירויות .

רגישות לרעש מדידה

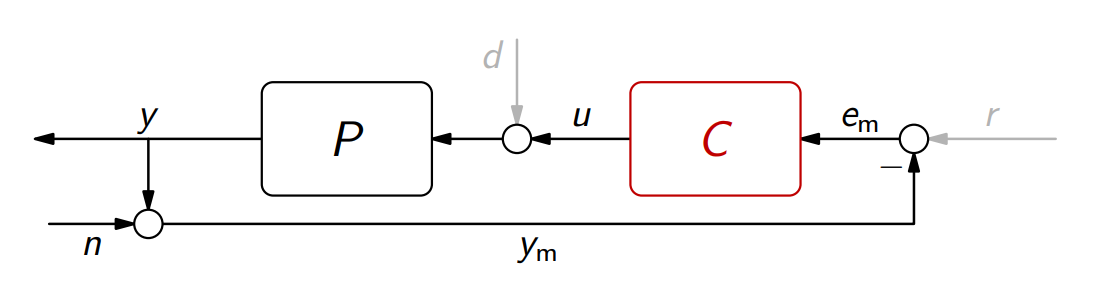
נסמן ב- את טווח התדירויות בו מרוכז. כדי לקבל רגישות לרעש מדידה נמוכה במצב מתמיד, אנו מבינים שצריך להתקיים:

כאשר היא התמרת לפלס של .
לכן, פונקציית הרגישות המשלימה צריכה לקיים:

כאשר נזכור ש- אם .

כיוון ש:

אם נדרוש , נקבל ש- , וככל ש- גדל, אז . זה מעיד על שהגבר גבוה בחוג לא יגרום לרגישות נמוכה לרעש מדידה. למעשה, ניתן להראות שאם אנו רוצים לחסום את השגיאה לרעש מדידה, למשל ע”י , אז נצטרך לדרוש:

ואז באמת:

לכל .
בגדול, כדי לקבל רגישות נמוכה לרעשי מדידה במצב מתמיד, נדרוש הגבר נמוך בחוג בטווח התדירויות .

עיצוב חוג

ראינו שמצד אחד, אנו צריכים הגבר גבוה בחוג, עבור ו-, ומצד שני, אנו צריכים הגבר נמוך ב- . למזלנו, ברוב המקרים יש הפרדה בין התדרים:

• אותות ייחוס הן “איטיות”, יענו בתדרים נמוכים.
• רעש מדידה הוא “מהיר”, יענו בתדרים גבוהים.

בנוסף, מאחר ורוב התהליכים הפיזיקליים הם low-pass, אנו צריכים לדאוג רק מהפרעות “איטיות”.

לכן, נרצה לעצב את החוג עם:

• הגבר חוג גבוה, , בתדרים “נמוכים”.
• הגבר חוג נמוך, , בתדרים “גבוהים”.

כלומר, נרצה שהגרף בודה של תיראה מהצורה:

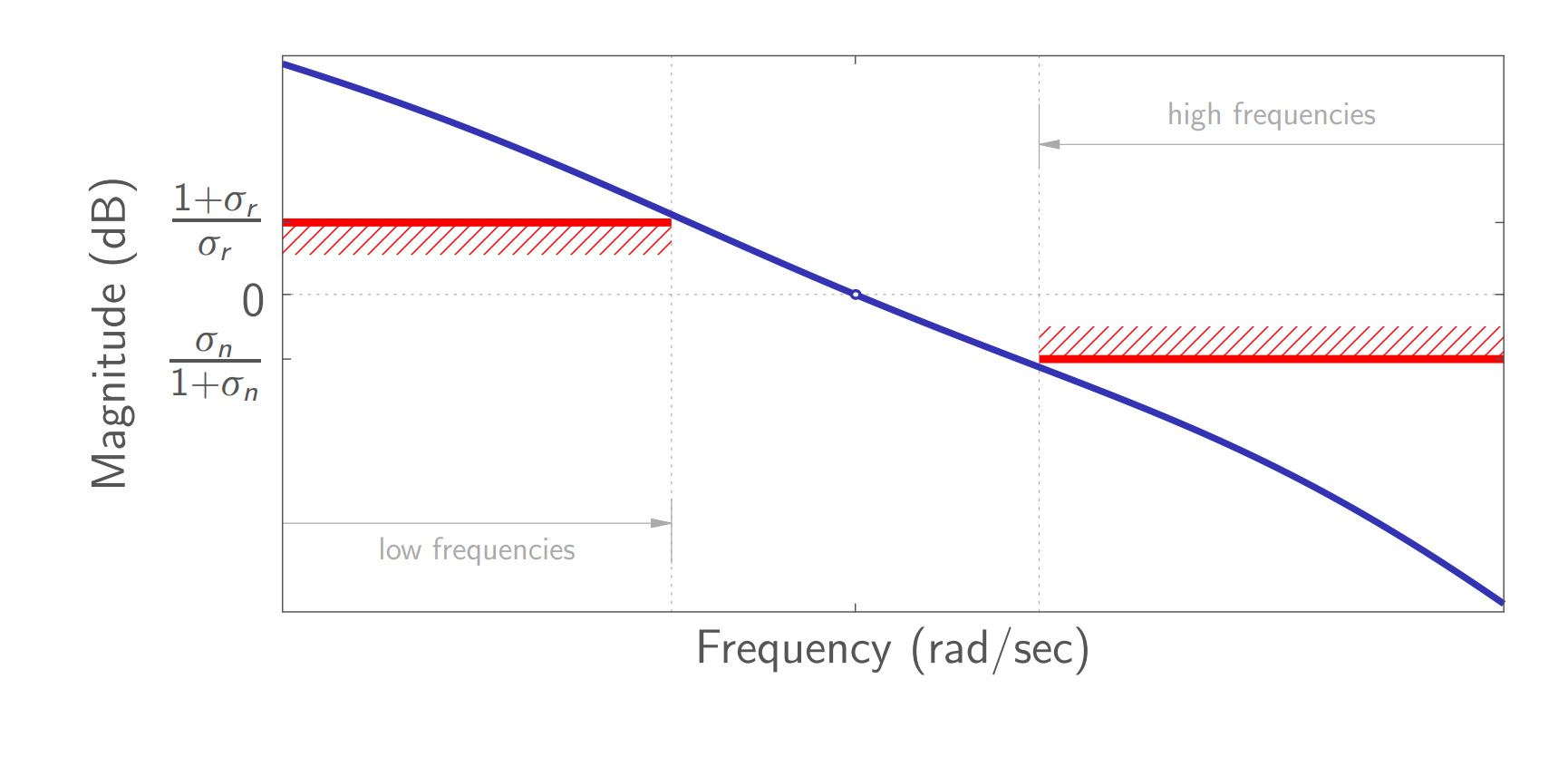
צורת גרף בודה-הגבר של רצויה. נשים לב שיש אזור בו הגבר החוג הוא לא גבוה ולא נמוך. (Leonid Mirkin’s Homepage, n.d.).

לאופן תכן זה אנו קוראים עיצוב חוג (loop shaping).

ביצועים בתגובת מעבר

אנו בעיקר מעוניינים בביצועי תגובת המעבר של אות היחוס:

ואנו מודדים אותו על בסיס תגובת מדרגה (המהירות שלה ומידת החלקלקות שלה).

אנו יודעים מניתוח תגובת תדירות שמאפייני תגובת המעבר במישור הזמן והתדירות הם:

• ככל שרוחב הפס של יותר רחב, תגובת המדרגה יותר מהירה.
• ככל שהרזוננס של יותר גבוה, נקבל תגובת-יתר או תגובת חסר יותר גדולה (overshoot ו-undershoot).

נוכל לבטא את תנאים אלו על בעזרת גרף פולארי. עבור כלשהו, הוא המרחק בין הנקודות ו- במישור המרוכב של :

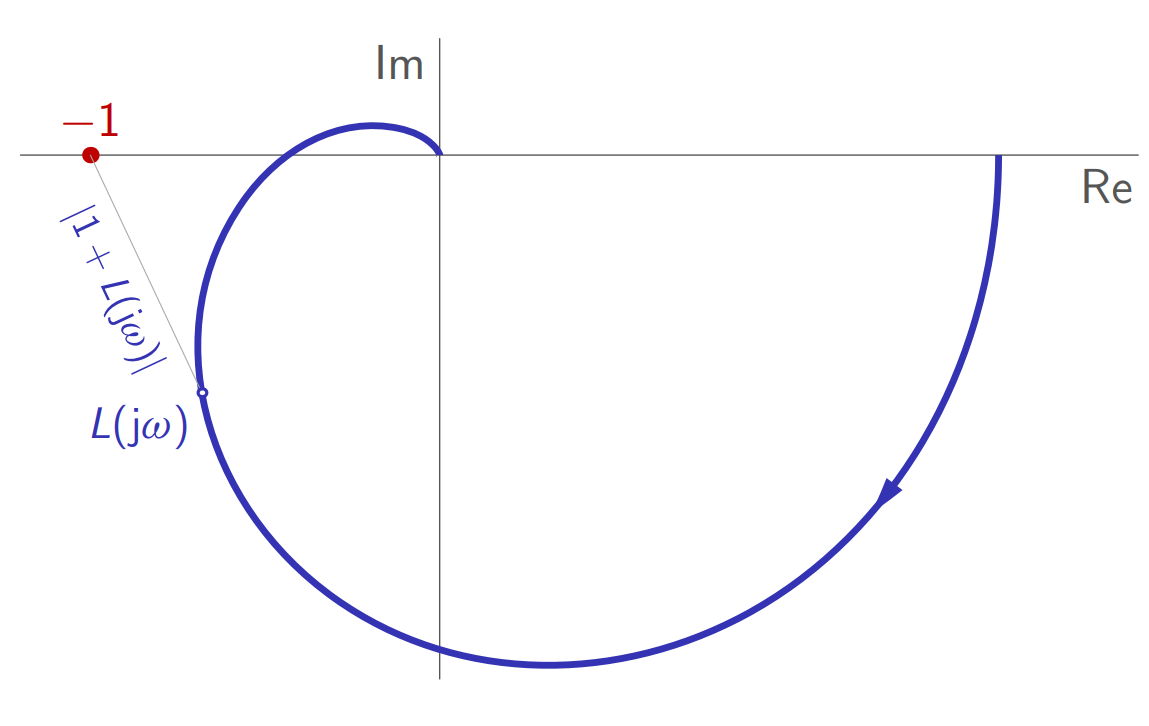
גרף פולארי של . (Leonid Mirkin’s Homepage, n.d.).

לכן, ככל ש- יותר קרוב ל- , ההגבר יותר גבוה. למשל, עבור

לערכי , הגרף הפולארי של ייראה מהצורה:

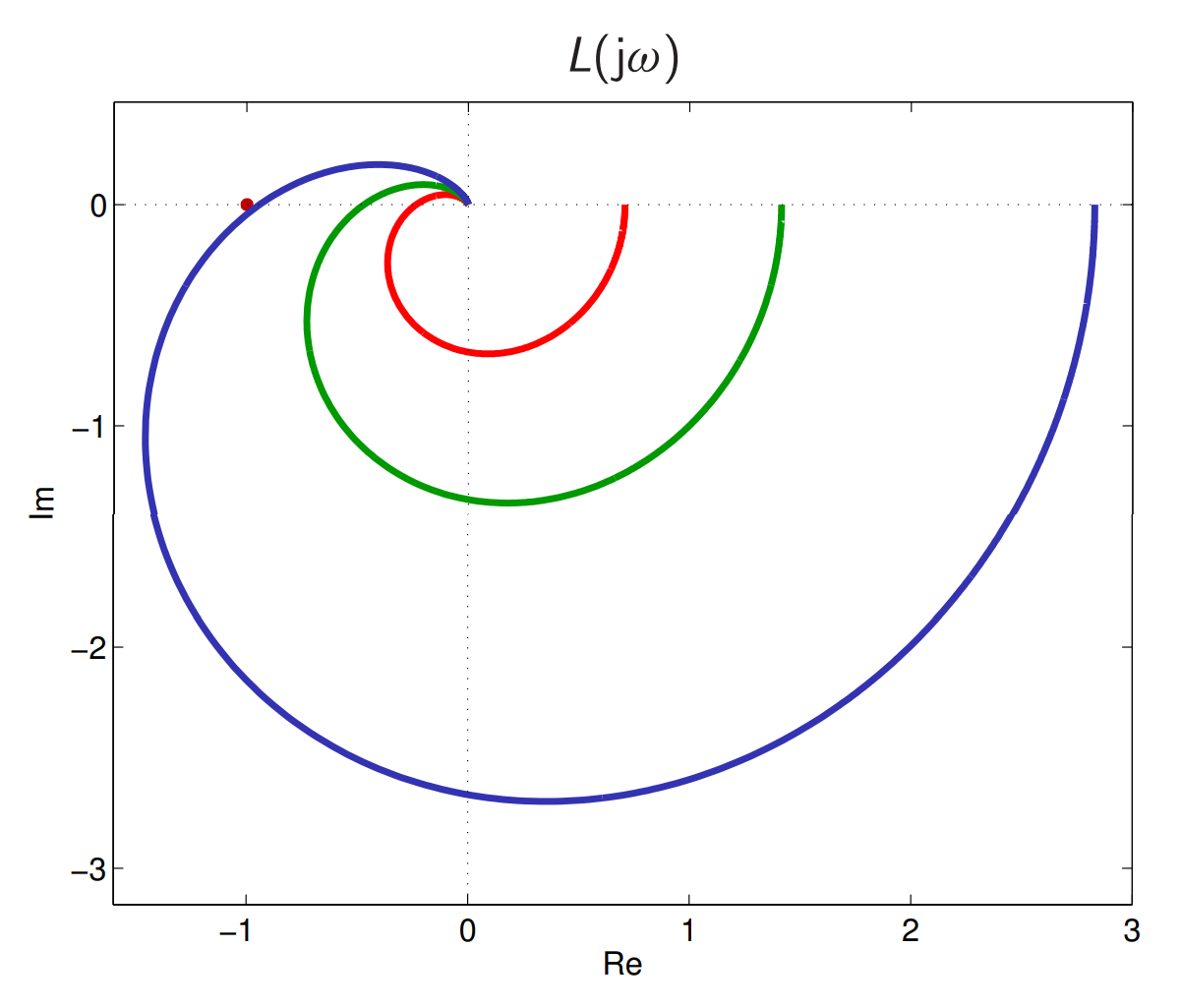
הגרף הפולארי של הנתון עבור ערכי שונים. (Leonid Mirkin’s Homepage, n.d.).

והגרף בודה-הגבר של יהיה:

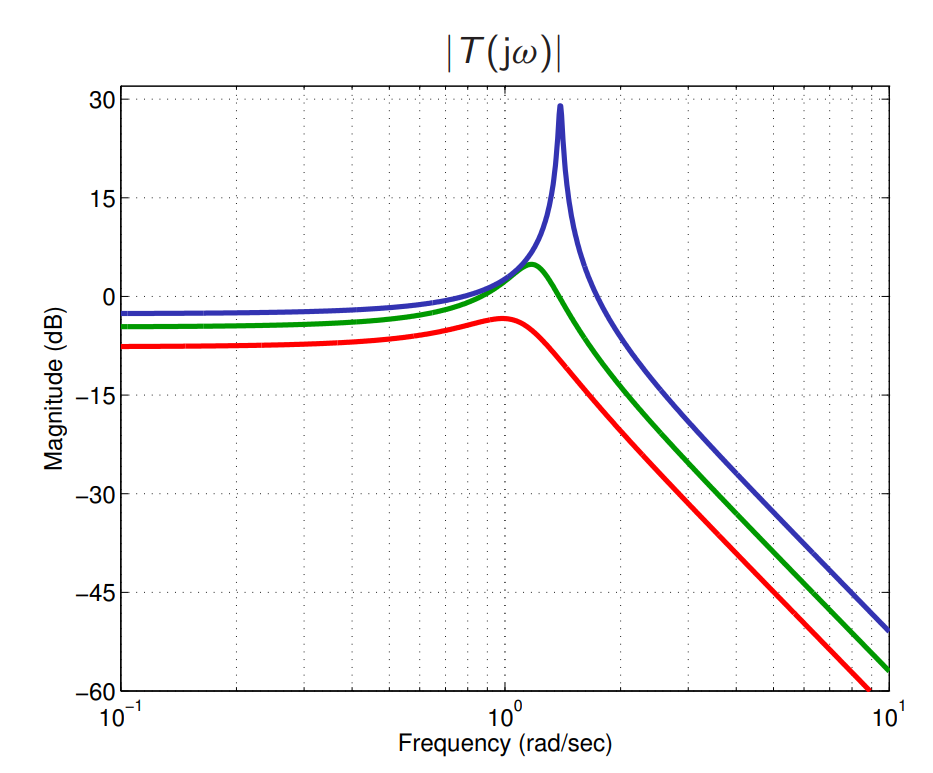
הגרף בודה-הגבר של עבור ה- הנתון. (Leonid Mirkin’s Homepage, n.d.).

אזור מעבר ותדירות מעבר

כאשר גדל, עובר מאזור בתדירויות נמוכות לאזור בתדירויות גבוהות:

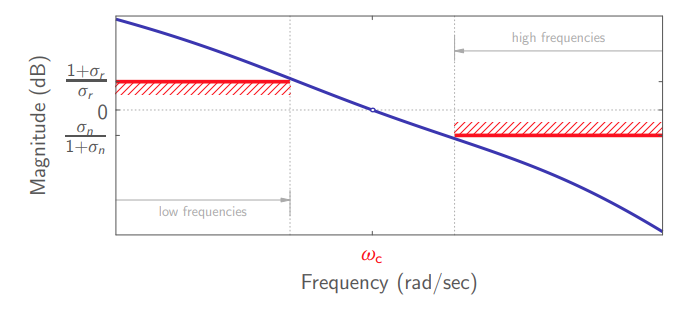
אזור מעבר ותדירות מעבר. (Leonid Mirkin’s Homepage, n.d.).

על הדרך, הוא עובר את האזור עם . אזור תדירויות זה נקרא אזור המעבר, והתדירות בה נקראת תדירות המעבר, והיא מסומנת ב-, כך ש:

יכולות להיות יותר מתדירות מעבר אחת.

אנו נרצה לעצב את בצורה הבאה:

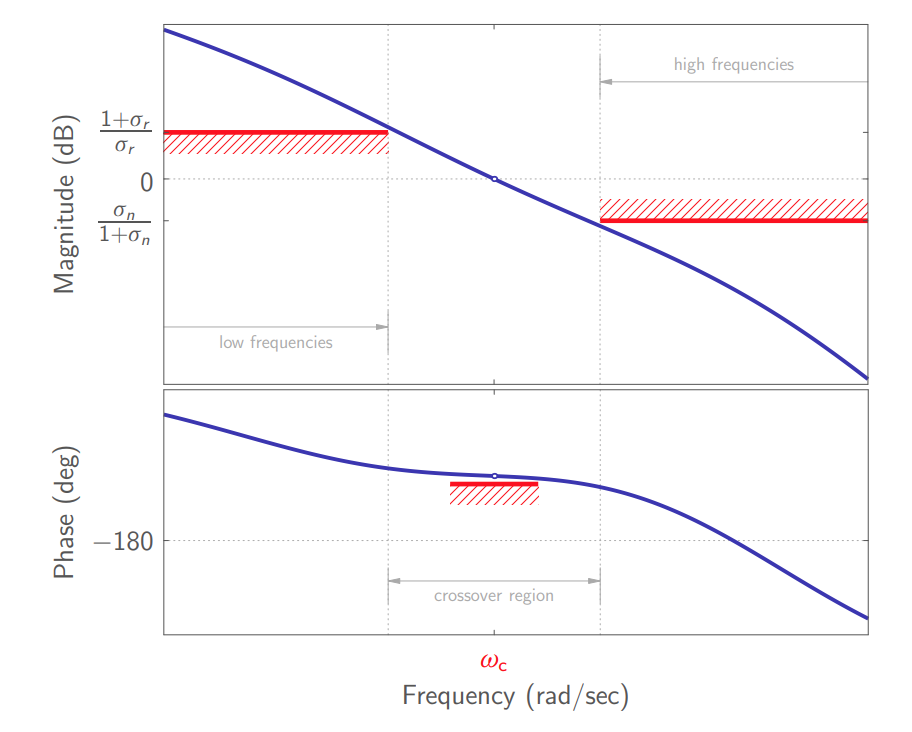
אופן עיצוב אידיאלי. (Leonid Mirkin’s Homepage, n.d.).

מאמץ בקרה בחוג סגור

מאמץ בקרה במצב מתמיד

עבור המערכת הבאה:

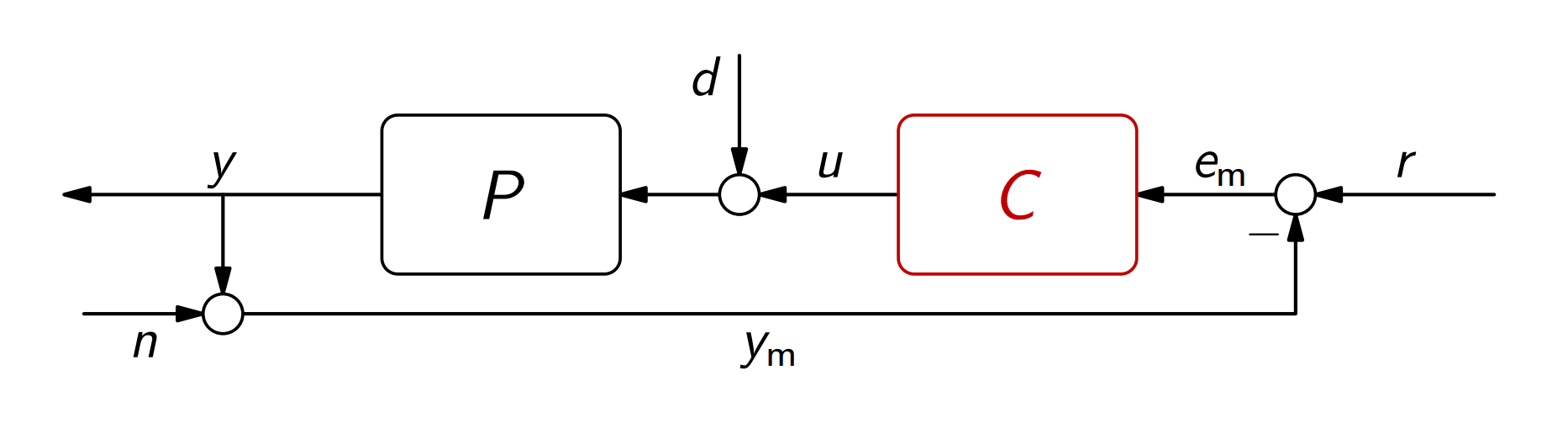
נזכור ממשוב יחידה ש:

לכן, המאפיינים של האות בקרה בחוג סגור תלויים במאפיינים של ו- (לעומת המאפיינים של בחוג הפתוח).

מבחינת האות ייחוס:

מאחר ו:

המאפיינים של נקבעים על ידי הקשרים בין הרוחבי פס המבוקרים ורוחבי הפס הלא מבוקרים.

למשל, אם גם ו- הם פילטרים low-pass ו-, אנו נצפה ש- גדל עם . לכן, אם , אנו נקבל ש- סביב , שיכול להיות שזה לא בתקציב שלנו.

מבחינת הרעש מדידה:

אם גדול עבור תדרים גבוהים, אנו במצב עוד יותר מסוכן מבחינת רעש המדידה, כי הוא לרוב בתדרים גבוהים.

מבחינת ההפרעות:

נרצה כמו מקודם להימנע מהגברים גבוהים של .

תרגילים

תרגיל 1

הביטו במשוב יחידה לעיל. האם הדרישות הבאות סותרות אחת את השנייה?
1.
\begin{cases}
\lvert {E}{r}(j\omega) \rvert <0.1\lvert R(j\omega) \rvert & & \forall \omega<10 \
\lvert {E}{n}(j\omega) \rvert <0.1\lvert N(j\omega) \rvert & & \forall \omega>1
\end{cases}$$

2. כאשרהואההשפעהשלאותהייחוסעלשגיאההמעקבהואההשפעהשלרעשההפרעהעליווהואערךהספקטרוםשלאותבתדירות

פתרון:
נשים לב כי מעצם הגדרת השגיאה :

עבור המקרה הראשון:
עבור הדרישה הראשונה, נעביר אגף:

באותו אופן, עבור השגיאה התחתונה:

נחבר ביחד את שתי האי שוויונות:

מאי שוויון המשולש:

קיימת סתירה, ולכן הדרישה לא אפשרית.

עבור המקרה השני:
במקרה זה אין סתירה, מכיוון ששני התנאים בכלל לא על אותם התדרים החופפים.

תרגיל 2

האיור הבא מתאר את הדיאגרמות הפולאריות של ארבעה תגובות תדירות של החוגים . מערכות אלו מבוקרות במשוב יחידה.

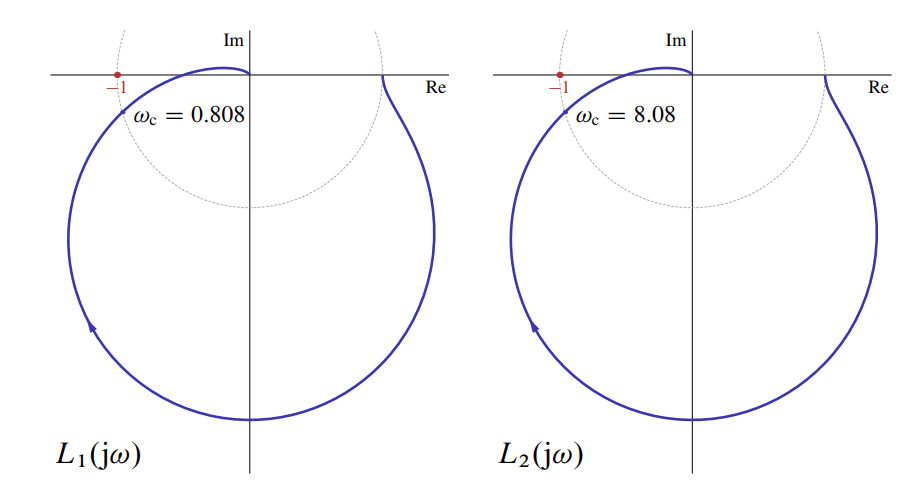
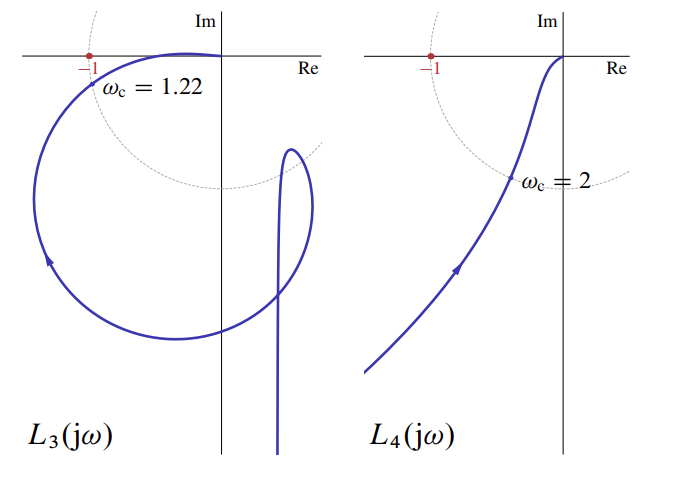
דיאגרמות פולאריות של . (Leonid Mirkin’s Homepage, n.d.).

סעיף א’

הגרפים הבאים הם גרפי בודה של פונקציות רגישויות משלימות . התאימו בין ו-.

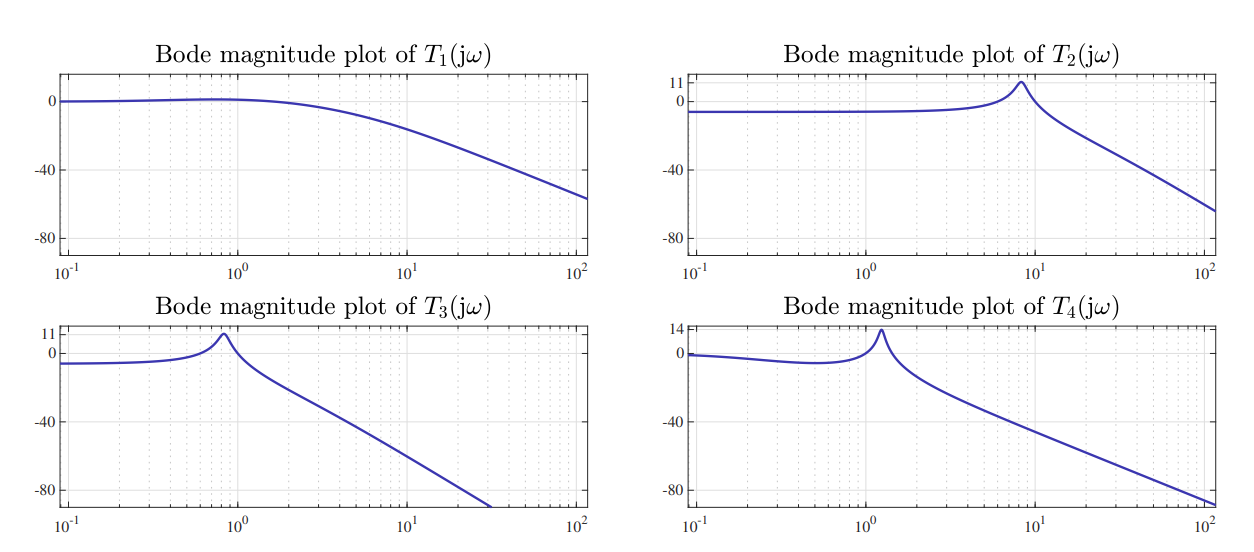
דיאגרמות בודה-הגבר של . (Leonid Mirkin’s Homepage, n.d.).

פתרון:
תדרי רזוננס מופיעים בעקומים פולאריים ובעקומי בודה נתאים ביניהם לפי תדר הרזוננס:

נשים לב ש- אינו מתקרב כמעט לנקודה הקריטית ולכן יש לו רזוננס נמוך, אם בכלל. לכן, .

סעיף ב’

הגרפים הבאים הם תגובות תדירות של פונקציות רגישות . התאימו בין ו-.

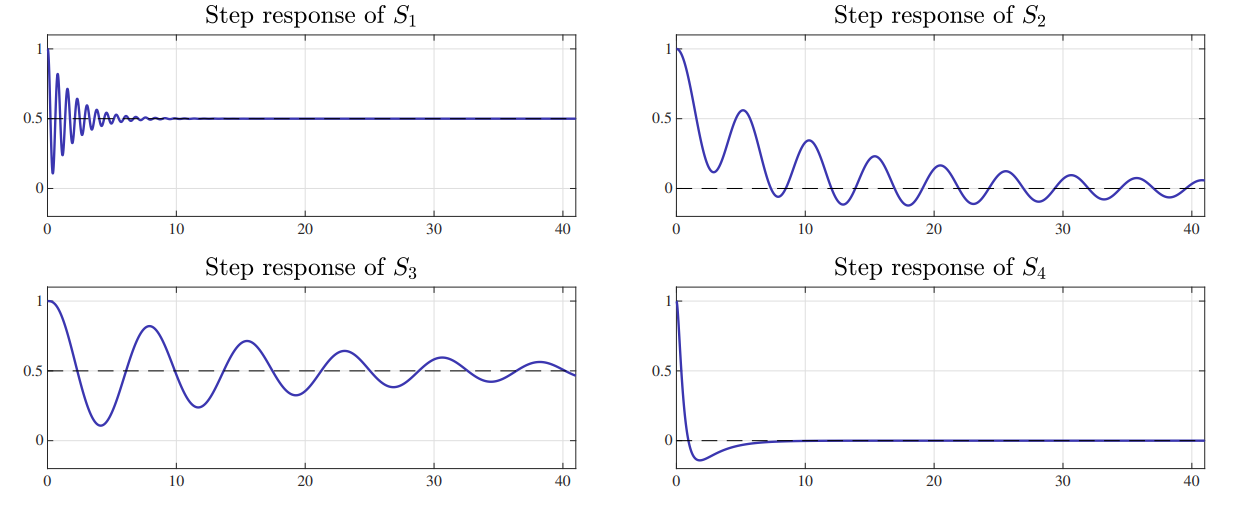
תגובות מדרגה של . (Leonid Mirkin’s Homepage, n.d.).

פתרון:
ככל שנתקרב לנקודה הקריטית, כך נתקרב למצב בו יהיה לנו קוטב בסביבת , ואז היינו רואים תגובה תונדת בתדר שקרוב ל-. המערכות יציבות כפי שניתן לראות, אך חלקן תונדות בתדרים מסוימים. לכן נתאים בין ל- לפי תדרים. נקבל 3 התאמות ראשונות כי לא תונדת.
התדר הכי מהיר הוא ב- ו-:

הבא אחריו הוא ב- ו-:

התדר האיטי ביותר הוא ב- ו-:

ל- אין תדר רזוננס (או אחד שניתן להבחין ב- ולכן התגובה של המערכת בחוג סגור אינה תונדת):

עוד רמז להתאמה הוא ערך השגיאה במצב מתמיד. שואף לאינסוף עבור , לכן שואפת לאפס במצב מתמיד, כמו ב-. עבור , מתקיים , ולכן , כמו שרואים ב-.

תרגיל 3

הביטו במערכת הבאה (שוב):

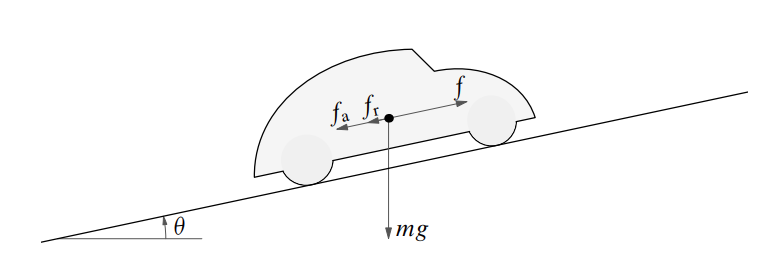
המערכת הנתונה על הרכב. (Leonid Mirkin’s Homepage, n.d.).

כפי שכבר ראינו, המודל לאחר לינאריזציה של המערכת, סביב נקודת שיווי משקל הוא:

סעיף א’

נרמלו את אות הבקרה והיציאה כך שלתהליך יש הגבר יחידה.

פתרון:
ננרמל לפי :

נקבל:

כעת, לתהליך יש הגבר יחידה:

גם את אות הייחוס ננרמל לפי :

בענף המשוב נרצה להעיף את הכפל ב- (משוב יחידה). את אות הייחוס נצטרך לחלק ב- כדי לקבל את . כדי לפתור זאת, ננרמל את הבקר עם כפל ב-. נשים לב גם שיציאת הבקר מוגברת פי , ולכן:

סעיף ב’

מצאו את רוחב הפס של התהליך המנורמל ושל הפונקציית רגישות משלימה (כפונקציה של ).

פתרון:
רוחב הפס הוא התדר בו , ותקף רק למערכות עם הפרש קטבים ואפסים חיובי ממש (כדי שבתדרים גבוהים ). אם יש כמה תדרים שמקיימים את התנאי של , נוהגים לבחור את התדר הראשון.

עבור פונקציית הרגישות, נשים לב כי:

ולכן רוחב הסרט:

עבור התהליך המנורמל:

כאשר נשווה ל- , נקבל:

סעיף ג’

מצאו את אות הבקרה (עבור כניסה מדרגה) ב-. בטאו את רוחב הפס של החוג הסגור כפונקציה של ורוחב הפס של התהליך המנורמל.

פתרון:
נמצא את אות הבקרה:

לפי משפט הערך ההתחלתי לכניסת מדרגה ( יציבה):

ננסה לבטא את בעזרת ו-. נשים לב שעבור :

נשים לב שמתחבא לנו כאן :

נבודד את :

כלומר ככל שהתדר עולה, כך גם . אם רוצים תגובה מהירה יותר, משלמים יותר במאמץ בקרה.

סעיף ד’

שרטטו את גרף הבודה של , , עבור .

פתרון:

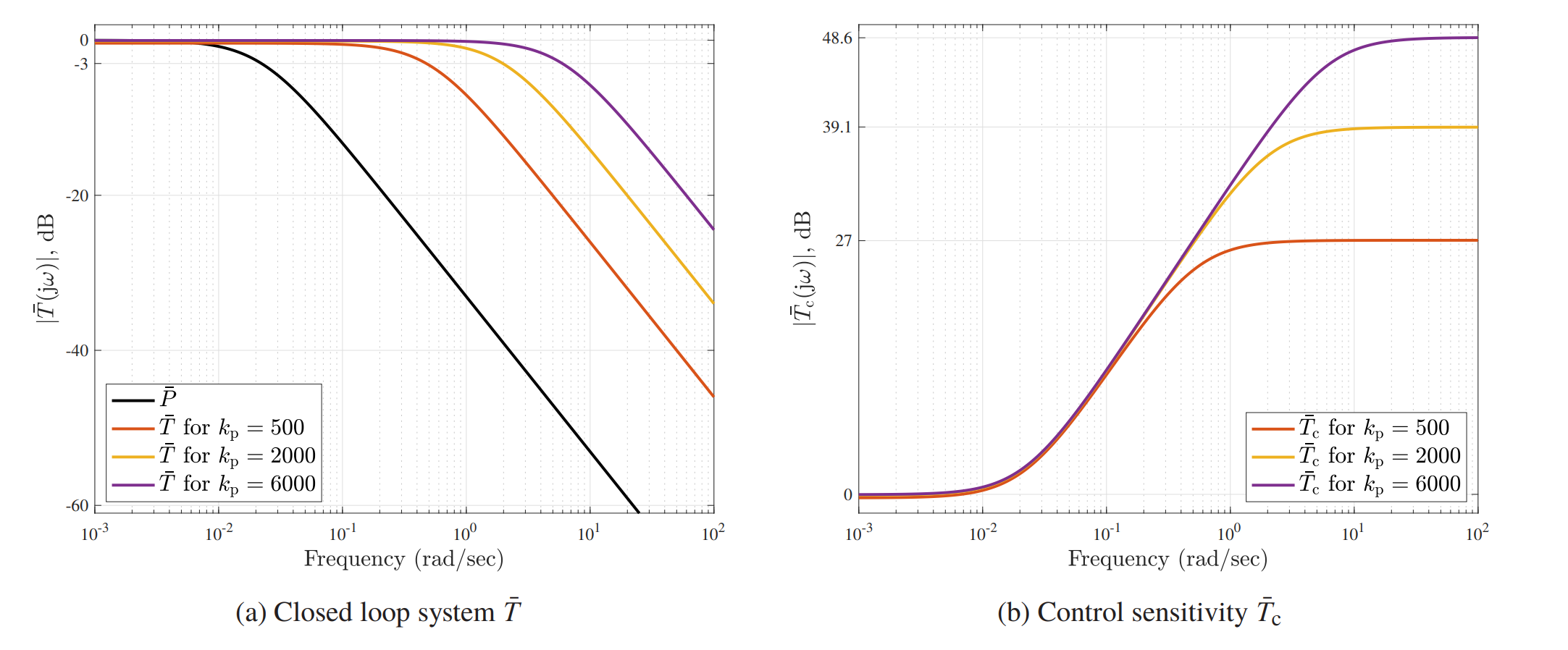
דיאגרמות בודה לתנאים בשאלה. (Leonid Mirkin’s Homepage, n.d.).

נשים לב שככל שמגדילים את , רוחב הפס של עולה. אבל, זה לא בא ללא מחיר - עולה גם כן, במיוחד בתדרים גבוהים, מה שהופך את המערכת לרגישה מאוד לרעשי מדידה.

→ קודם: ICT1_007הבא: ICT1_009 ←