ICT1_009 יציבות בעיצוב חוג

→ קודם: ICT1_008הבא: ICT1_010 ←

קריטריון נייקוויסט

כדי לפשט את הדרישות שלנו על החוג הסגור, נחליף את

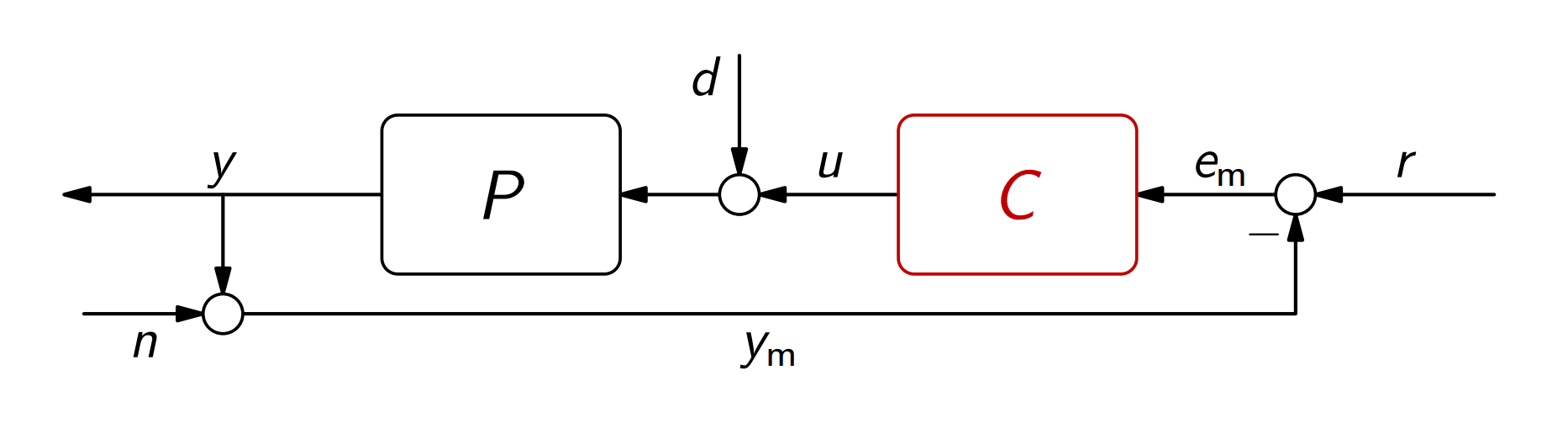
ב:

בעיצוב החוג הסגור אנו רוצים:

• תדירות מעבר מתאימה. גבוה מספיק כך שנקבל תגובות מספיק מהירות ושנוכל לעקוב אחר טווח רחב של אותות ייחוס, אבל לא גבוה מדי כדי להימנע מהגברת רעשי מדידה ומאמצי הגברה משמעותיים.
• הגבר גבוה () בתדרים נמוכים .
• הגבר נמוך () בתדרים גבוהים ().
• הרחקת מהנקודה באזור המעבר.
• יציבות יציבות יציבות.

כדי לקבל את התנאי האחרון, היציבות, אנו יכולים להיעזר בפולינום האופייני של המערכת, או בעזרת שיטת המג”ש, אבל אף אחד מהם לא עושה זאת במובנים של תגובת תדירות של , שזה מה שעיצוב חוג צריך - הם עושים זאת בעזרת הפולינום האופייני. לכן, נפתח שיטה למציאת יציבות של חוג במובנים של .

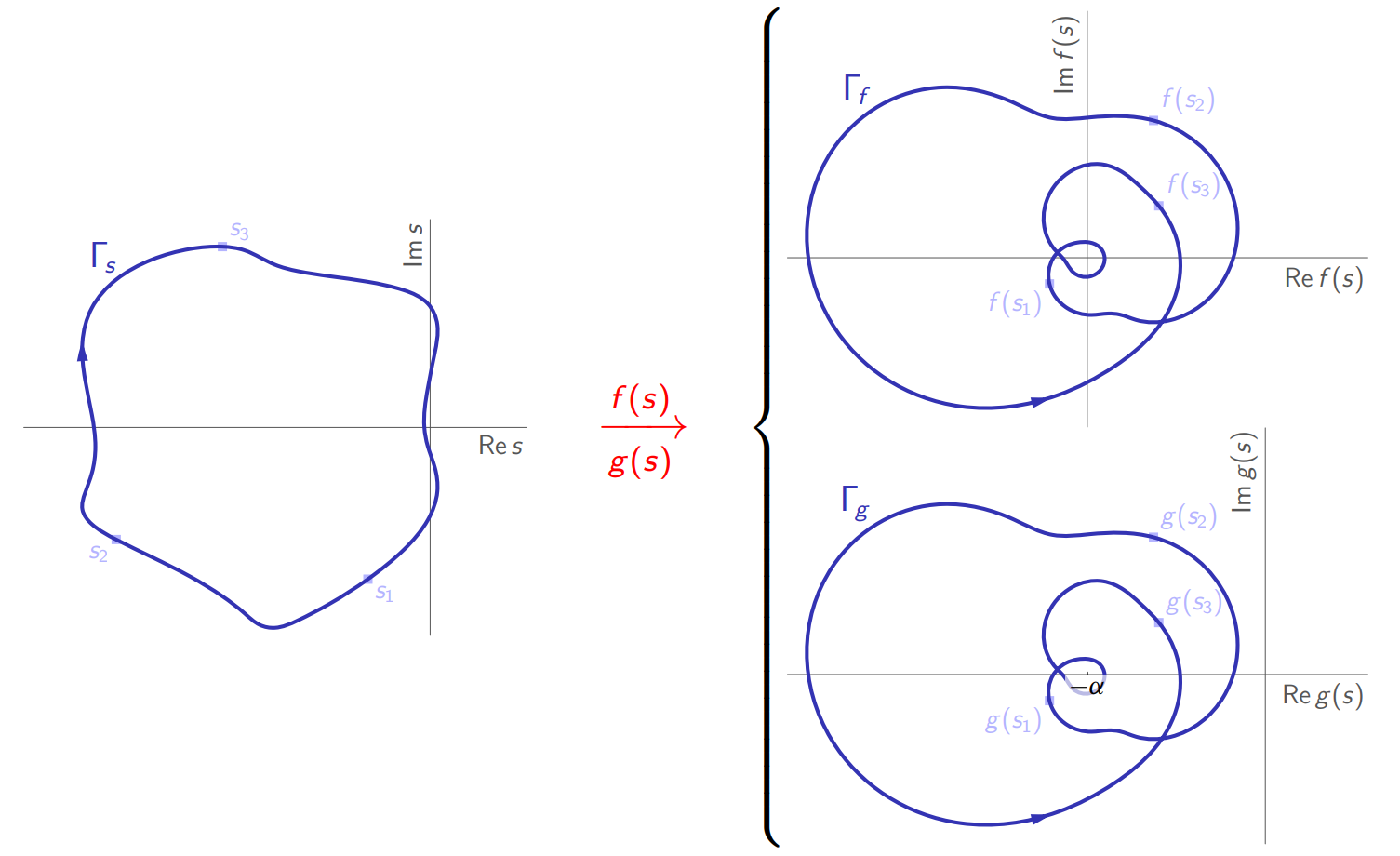
עיקרון הארגומנט של קושי

תהי פונקציה מרוכבת . לכל מהמקור שלה, גם . אנו אומרים ש- מועתקת ע”י ממישור למישור .

העתקה של מספר נקודות. (Leonid Mirkin’s Homepage, n.d.).

אם נבצע את ההעתקה לרצף של נקודות , למשל עבור עקומה הנמצאת במישור , ההעתק שלה גם יהיה עקומה במישור :

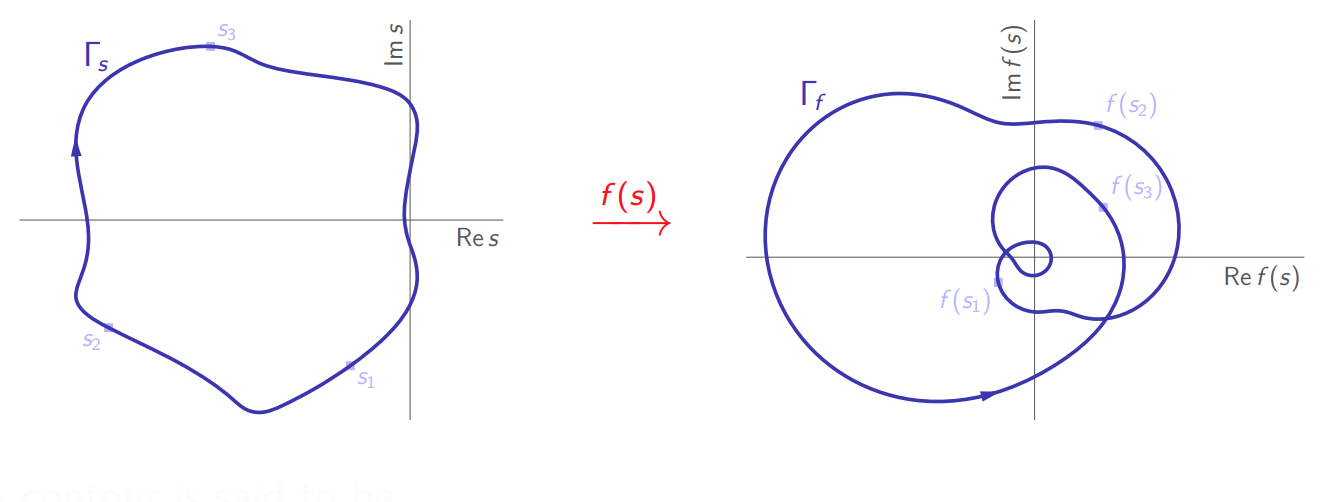
העתקה של עקומה סגורה פשוטה. (Leonid Mirkin’s Homepage, n.d.).

כמו בחדו”א, נאמר שעקומה היא פשוטה אם היא לא חותכת את עצמה, ונאמר שהיא סגורה אם היא מתחילה ומסתיימת באותה הנקודה. מבין העקומות לעיל, פשוטה וסגורה, בעוד סגורה אבל לא פשוטה.

משפט:

תהי עקומה פשוטה וסגורה, מרומורפית (meromorphic) (כמו גזירה למקוטעין לפונקציות מרוכבות) בתוך ו-על , הוא מספר האפסים של בתוך , ו- הוא מספר הקטבים של בתוך . אזי:
אם לא עובר דרך האפסים או הקטבים של , אז מקיף את הראשית פעמים עם כיוון השעון כאשר מתקדמת ב- עם כיוון השעון.

למשל, עבור

עם קטבים ו- בתוך :

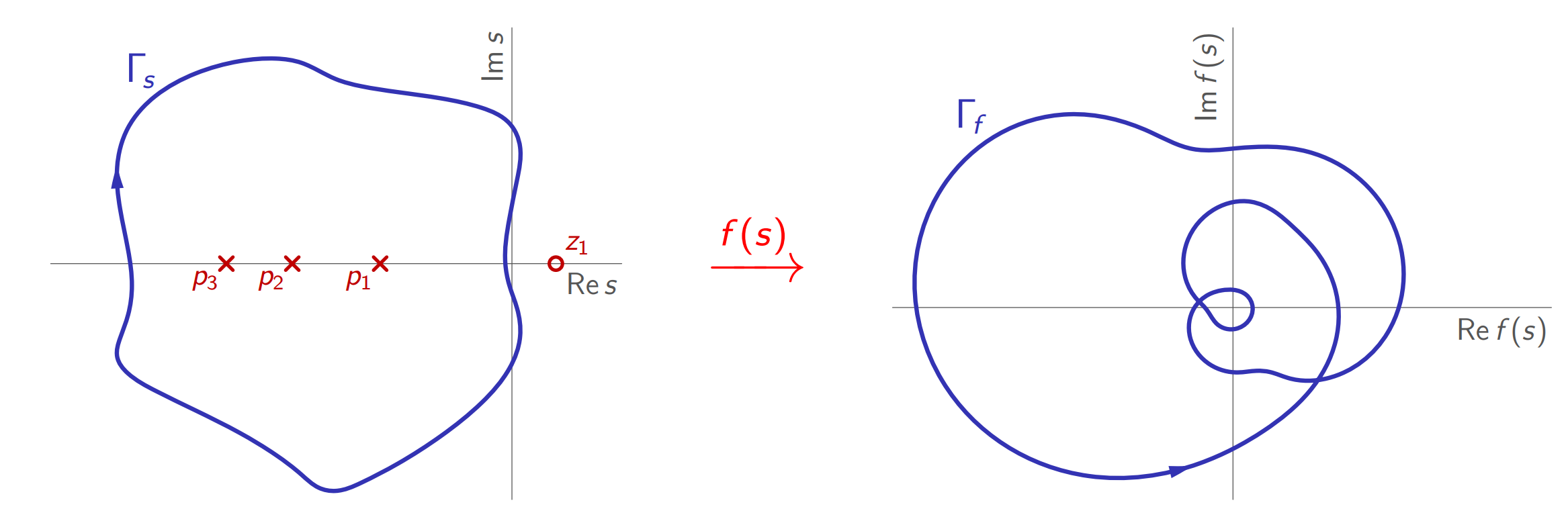
העתקה על עקומה . (Leonid Mirkin’s Homepage, n.d.).

לכן מקיף את הראשית פעמים עם כיוון השעון (כך שהוא מקיף אותו פעמים נגד כיוון השעון).

נוכל גם להפעיל את אותו העיקרון אם ישנה הזזה בקבוע. למשל, אם ל- כלשהו, אז:

העתקה ו-. (Leonid Mirkin’s Homepage, n.d.).

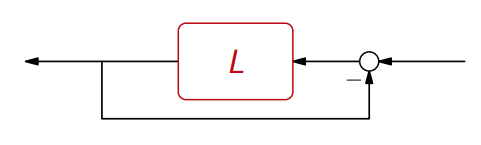
פונקציית ה-return difference

יהי

שראינו בפרק קודם - פונקציית התמסורת של החוג. נניח כי אין צמצומים לא יציבים בין ו-. נביט כעת בפונקציית תמסורת הבאה:

הנקראת return difference. מהקשר לעיל ניתן לראות ש:

• קטבים לא יציבים של הם קטבים לא יציבים של החוג הפתוח.
• אפסים לא יציבים של הם קטבים לא יציבים של החוג הסגור.

נביט במערכת הבא:

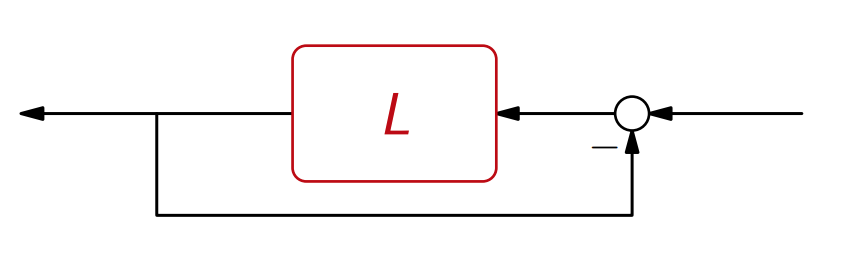
נניח כי הוא proper ואין לו קטבים בציר (נוריד את ההנחה האחרונה בהמשך).

בהמשך הפרק אנו הולכים לבצע את השלבים הבאים:

1. נגדיר עקומה סגורה פשוטה המכילה את כל הקטבים הלא יציבים - כל הקטבים ב-RHP הפתוח ().
2. נמצא את ההעתקה של ע”י ה-return difference ().
3. נספור את מספר הסיבובים עם כיוון השעון של הראשית ע”י העקום .

לפי עיקרון הארגומנט של קושי:

כאשר:

• המספר הוא מספר הקטבים של החוג הסגור ב- .
• המספר הוא מספר הקטבים של החוג הפתוח (של ) ב-.

האם נעביר אגפים במשוואה לעיל:

אנחנו רוצים ש- , כי אז לא יהיו קטבים לא יציבים בחוג הסגור. לכן, על כל קוטב לא יציב בחוג הפתוח, אנחנו רוצים סיבוב נגד כיוון השעון שיפצה עליו (שוב, נחשב חיובי עבור הקפות עם כיוון השעון).

ראינו שהקשר בין המישור והמישור הוא רק הזזה אופקית ב-:

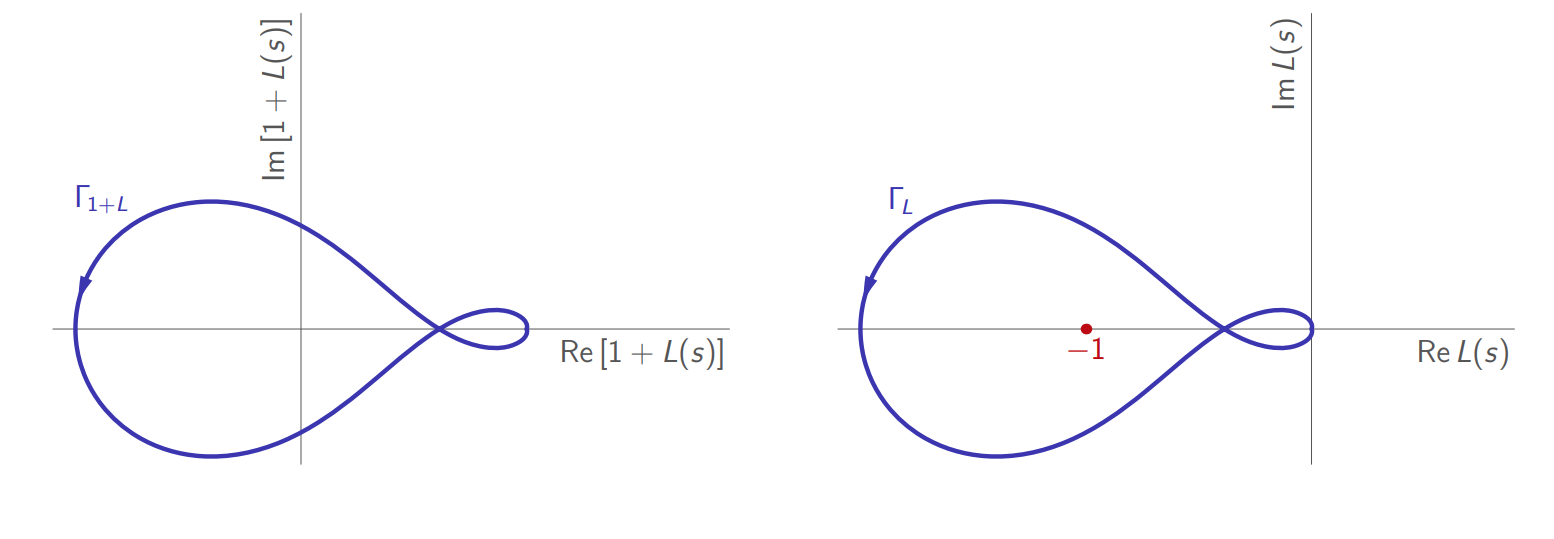
הזזה אופקית במישור.

לכן, מספר ההקפות סביב הראשית של הוא מספר ההקפות של סביב . מעתה נעבוד עם מישור , ונתייחס לנקודה כנקודה הקריטית.

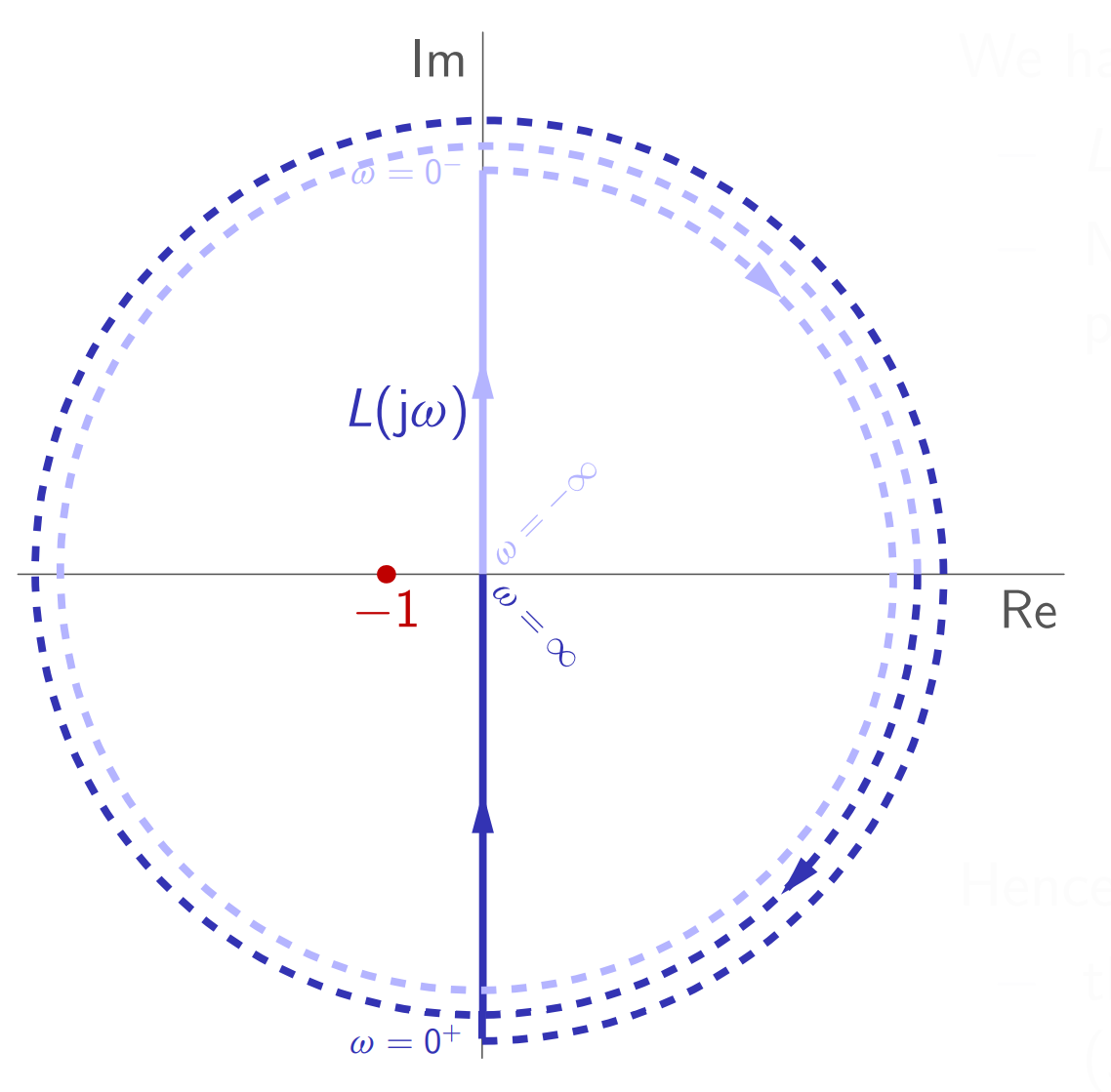
עקום נייקוויסט

העקום

כאשר

נקרא קונטור נייקוויסט, כאשר . הוא כולל את כל הקטבים ב-RHP הפתוח של פונקציות תמסורת עם מספר סופי של קטבים.

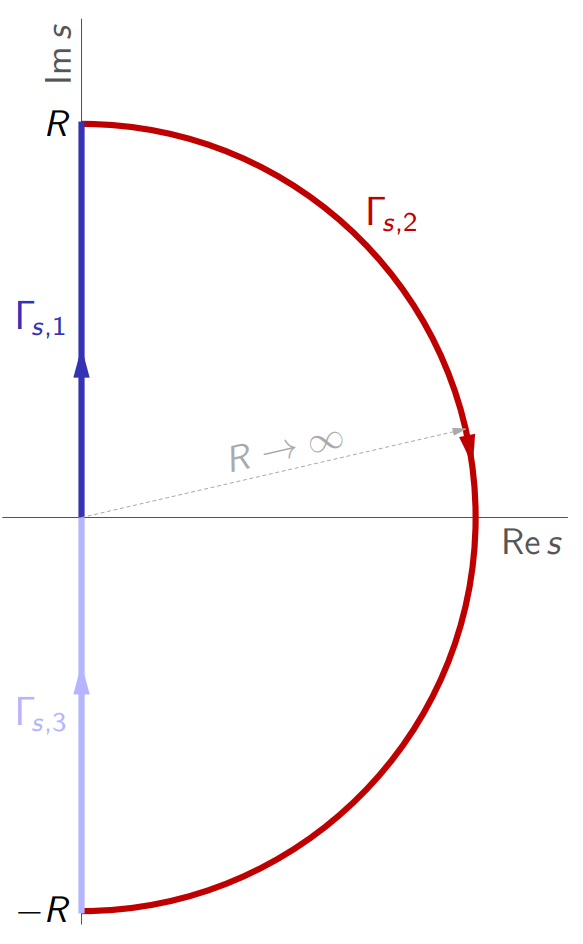
קונטור נייקוויסט.

כעת נרצה לדעת מהי ההעתקה של קונטור נייקוויסט לפי פונקציה כלשהי .

• עבור :
  במקרה זה , כך שהתמונה שלו היא , כך שלמעשה הוא הגרף הפולארי של תגובת התדירות של .
• עבור :
  מאחר ו- הוא proper: ניתן להראות שעבור , נקבל לכל , כך ש- הוא נקודה יחידה . מאחר ונקודה זו כבר שייכת ל-, נוכל להתעלם מ-.
• עבור :
  זהו מקרה זהה ל-, רק עם במקום , ולכן הוא הצמוד (מראה) של הגרף הפולארי סביב הציר הממשי.

האיחוד של ו-, שהוא הגרף של בקואורדינטות פולאריות כאשר רץ מ- ל-, נקרא עקום נייקוויסט של .
נוכל לבנות את עקום זה בשני שלבים:

1. נבנה את הגרף הפולארי של (שהוא הגרף של בקואורדינטות פולאריות כאשר רץ מ- עד ).
2. נוסיף את המראה של הגרף הפולארי סביב הציר הממשי.

קריטריון יציבות נייקוויסט

משפט:

המערכת בחוג סגור יציבה אמ”ם עקום נייקוויסט של :

• לא חותכת את הנקודה הקריטית .
• סובבת סביב הנקודה הקריטית פעמים נגד כיוון השעון כאשר גדל מ- ל-, ו- הוא מספר הקטבים של ב-.

עיקרון ראשון:
אם עקומת נייקוויסט של לא חותכת את הנקודה הקריטית, אז מספר הקטבים הלא יציבים בחוג הסגור הוא:

כאשר הוא מספר ההקפות עם כיוון השעון של הנקודה הקריטית ע”י עקום נייקוויסט.

עיקרון שני:
עם עקומת נייקוויסט של חותכת את הנקודה הקריטית בתדירות מסוימת , אז ל- יש לפחות שורש אחד ב- (על הציר המדומה).

עיקרון שלישי:
אם יציב, אז המערכת בחוג סגור יציבה אמ”ם הגרף הפולארי של לא חותך ולא מקיף את הנקודה הקריטית כאשר רץ מ- ל-.

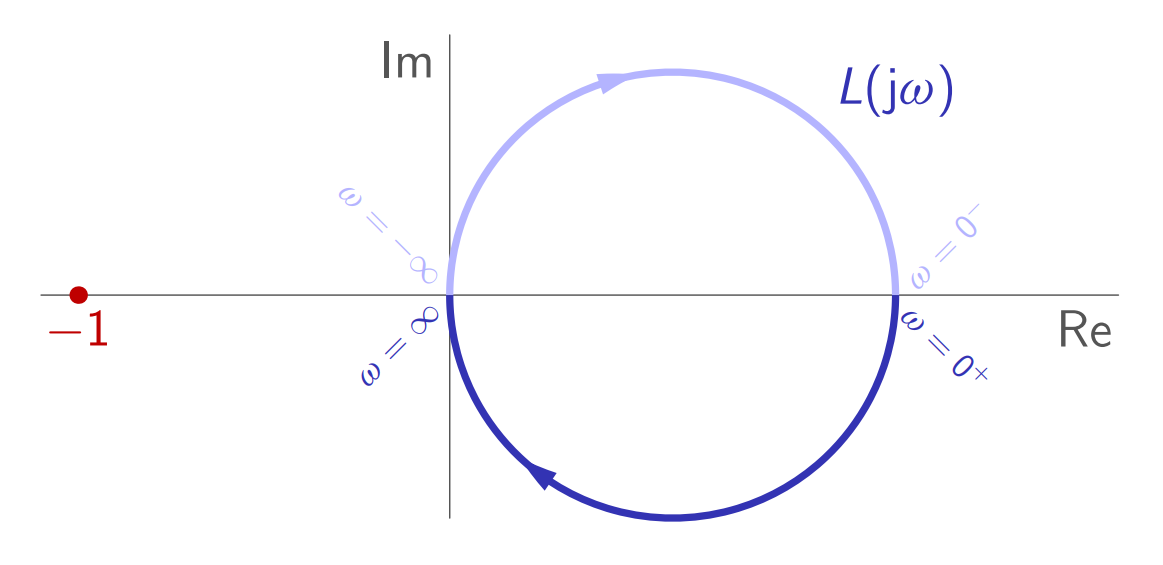
דוגמה:

יהי . העקום נייקוויסט שלו הוא:

קיבלנו ש- הוא יציב (כי ), וגם העקום נייקוויסט לא סובב את הנקודה הקריטית. לכן, המערכת בחוג סגור יציבה.

דוגמה:

יהי . העקום נייקוויסט שלו הוא:

קיבלנו ש- הוא יציב (כי ), וגם העקום נייקוויסט לא סובב את הנקודה הקריטית. לכן, המערכת בחוג סגור יציבה.

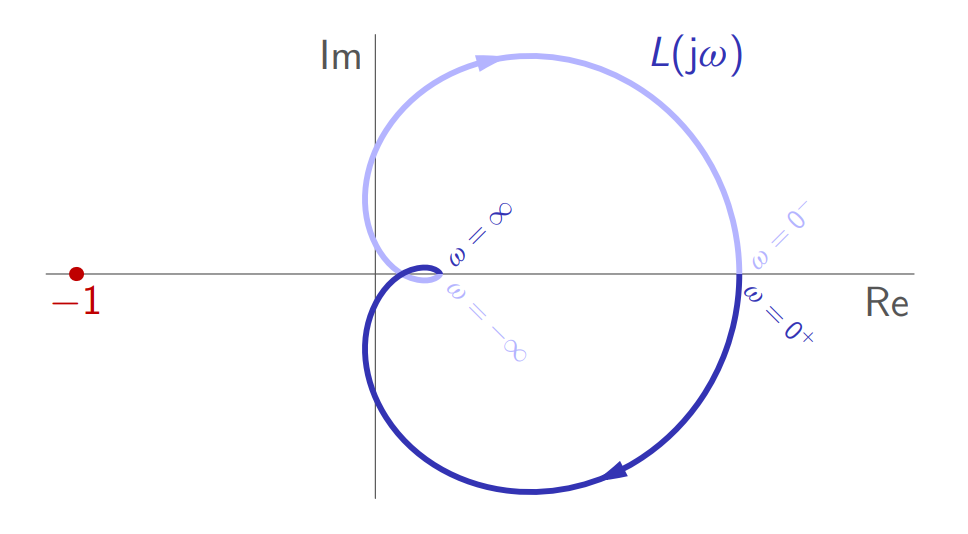
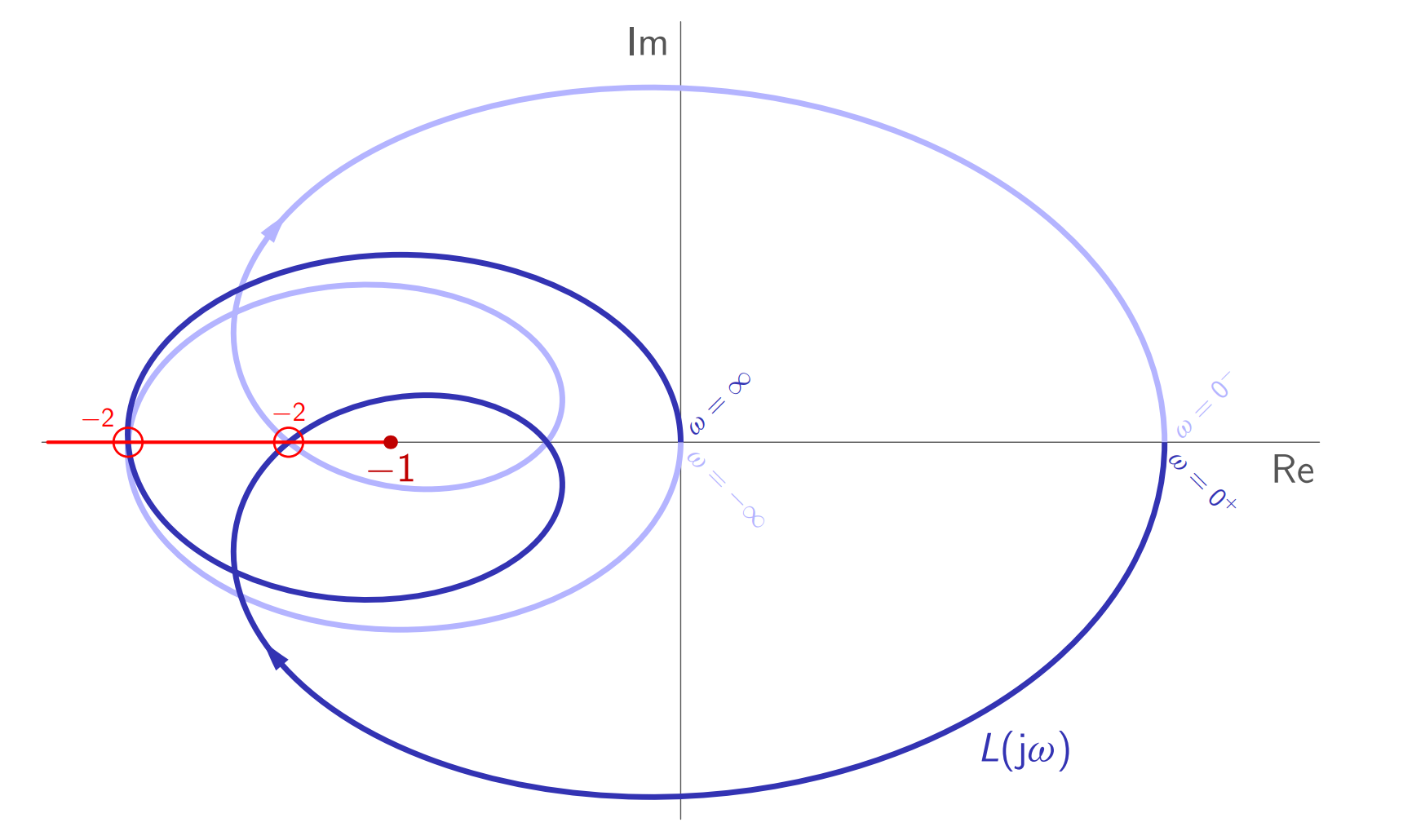
דוגמה:

יהי . העקום נייקוויסט שלו:

קיבלנו ש- לא יציב עם קוטב אחד לא יציב (אז ). בנוסף, העקום נייקוויסט סובב את הנקודה הקריטית פעם אחת נגד כיוון השעון. לכן, המערכת בחוג סגור יציבה.

מומלץ לראות את הדוגמאות הנוספות במצגת.

עקום נייקוויסט כללי

עד כה הנחנו של- אין קטבים בראשית, ואז אנו יכולים להשתמש בעיקרון הארגומנט של קושי עם קונטור נייקוויסט שהגדרנו. אם יש קוטב בראשית, עלינו להגדיר את קונטור זה באופן קצת שונה:

כאשר

עם וגם . קונטור זה עדיין כולל את כלל הקטבים ב-RHP הפתוח של פונקציות תמסורת עם מספר סופי של קטבים.

ההעתקה של לא משתנה, אז עלינו רק לסיים את התמונה עם:

• עבור :
  יהי , כאשר ו- הוא סופי - כלומר, הוא מספר האינטגרטורים. במקרה זה: כך ש- הוא עקום ברדיוס , המתחיל חיובי (אם ) או שלילי (אם ) בציר הממשי, וממשיך ל- עם כיוון השעון, עד שהוא חותך את התחלת .
• עבור :
  מאחר ו- יש מקדמים ממשיים, , ולכן הוא מראה של סביב הציר הממשי.

הערה:

האיחוד הוא קשת המחברת את הקצוות של וההתחלה של דרך הזווית עם כיוון השעון.

כעת, כיוון שהקונטור נייקוויסט המתוקן לא כולל את הקטבים של בראשית, לא נספור את קטבים אלו ב-. נוכל לעשות זאת כי ל- אין שורשים ב-, ולכן כל הקטבים הלא יציבים של החוג הסגור נמצאים בתוך קונטור נייקוויסט המתוקן אם קטן מספיק.

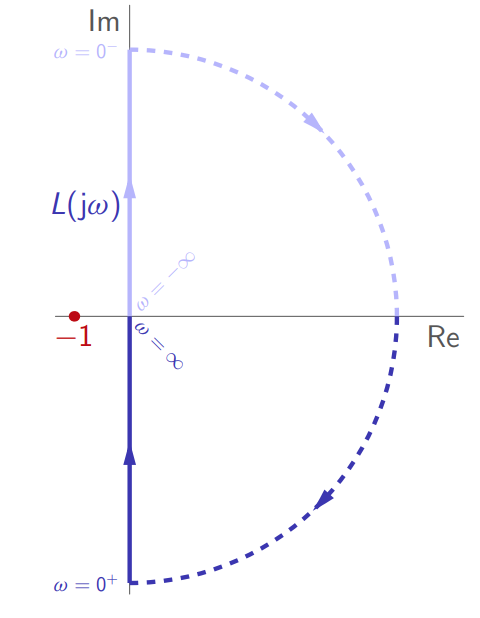
דוגמה:

יהי . העקום נייקוויסט שלו:

קיבלנו ש- “יציב” (), והעקום נייקוויסט שלו לא מקיף את הנקודה הקריטית. לכן, המערכת בחוג סגור יציבה.

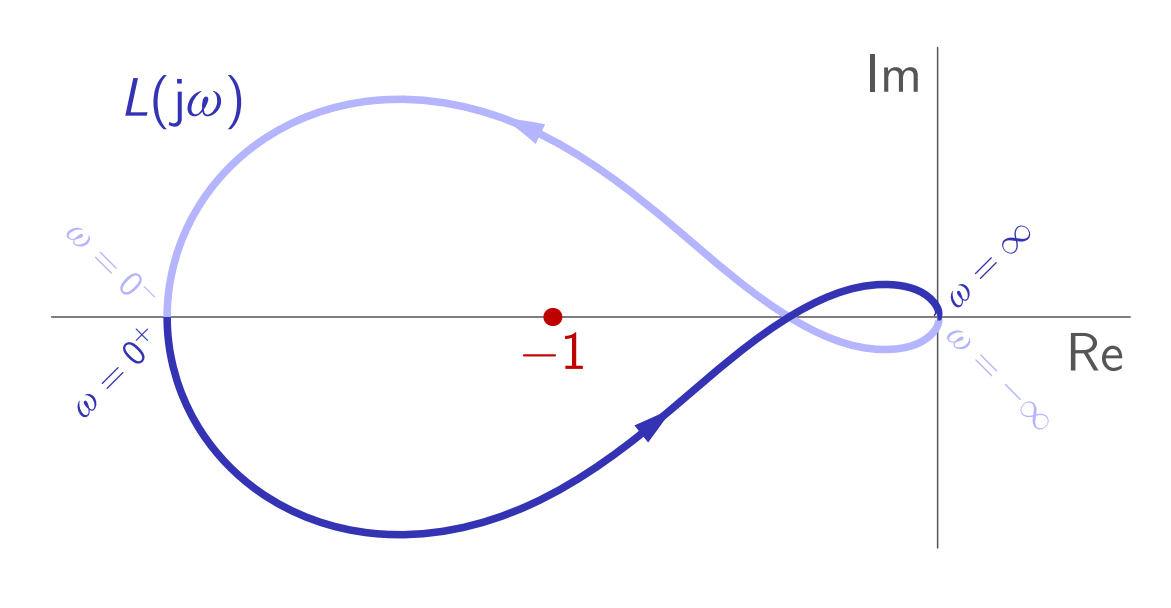
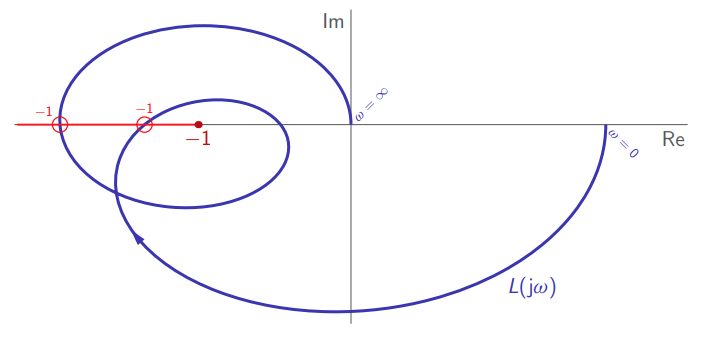
דוגמה:

יהי . העקום נייקוויסט שלו הוא:

קיבלנו ש- “יציב” (), והעקום נייקוויסט שלו סובב את הנקודה הקריטית פעמיים עם כיוון השעון. לכן, המערכת בחוג סגור לא יציבה ().

מומלץ לראות את הדוגמאות הנוספות במצגת.

פישוטים על הקריטריון ליציבות

ספירת ההקפות נגד כיוון השעון בגרף מסועף יכולה להיות בעייתית:

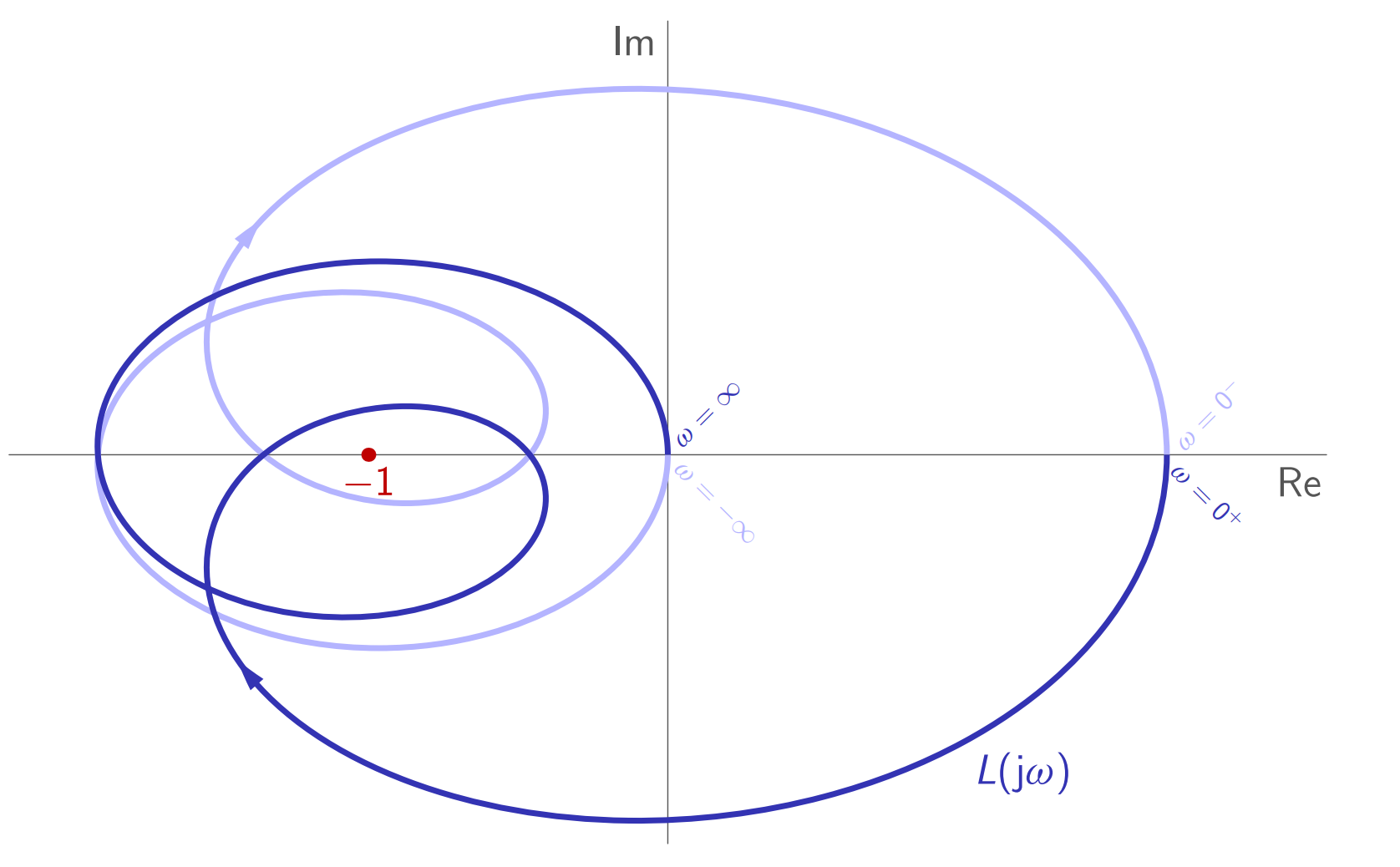
עקומת נייקוויסט מעצבנת לניתוח. יש במקרה זה סיבובים נגד כיוון השעון.

אבל, בעזרת טופולוגיה, ישנה שיטה לפישוט מציאת מספר ההקפות.

תהי קרן במישור ה-:

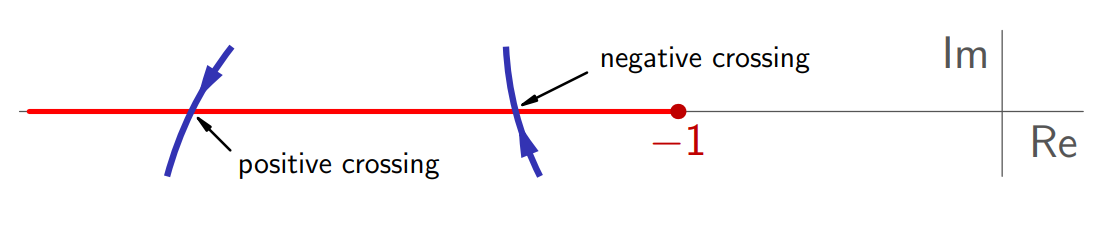
נאמר שישנו חיתוך כאשר העקומה של חותכת את הקרן. נאמר שהחיתוך חיובי אם כיוון הוא כלפי מטה, ונאמר שהחיתוך שלילי אם כיוון הוא כלפי מעלה.

למה:

מספר ההקפות נגד כיוון השעון סביב הנקודה הקריטית ע”י עקום נייקוויסט של שווה למספר החיתוכים עם הקרן ע”י עקום נייקוויסט של .

חיתוכים של עקום נייקוויסט עם הקרן .

למה:

מספר ההקפות נגד כיוון השעון סביב הנקודה הקריטית ע”י עקום נייקוויסט של שווה לפי- מספר החיתוכים עם הקרן ע”י הגרף הפולארי של .

חיתוכים של הגרף הפולארי עם הקרן .

עלינו להיזהר ממקרים בהם הגרף הפולארי מתחיל או מסתיים על הקרן. במצבים אלו, נחשיב את נקודות אלו כ-”חצי חיתוך”.

ניתוח חוגים

בהנחה ויש לנו מערכת מהצורה:

כאשר הוא פונקציית תמסורת proper ו- הוא פרמטר שאנו רוצים לבחור. אנו רוצים למצוא את כל ה- עבורו הוא יציב - מאוד דומה לרעיון המג”ש.

נוכל לרשום את פונקציית התמסורת return difference כ:

מאחר וההכפלה ב- לא משפיעה על הקטבים או האפסים של פונקציית תמסורת זו, נוכל לנתח את היציבות שלה ע”י ההעתקה של קונטור נייקוויסט ע”י . במילים אחרות זה אומר שאנו צריכים לנתח את העקומת נייקוויסט של עם הנקודה הקריטית .

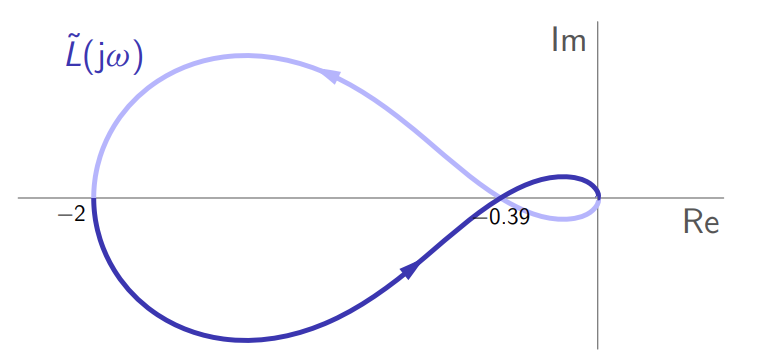
דוגמה:

יהי . העקום נייקוויסט שלו הוא:

במקרה זה, , וישנם ארבעה קטעים שונים של עבורם נקבל יציבויות שונות:

• עבור , אין הקפות, ולכן .
• עבור , יש הקפה אחת נגד כיוון השעון, ולכן .
• עבור , יש הקפה אחת עם כיוון השעון, ולכן .
• עבור , אין הקפות, ולכן .

תרגילים

תרגיל 1

התהליך

מבוקר בחוג סגור (משוב יחידה) ע”י בקר פרופורציונלי . מצא -ים המייצבים את המערכת ע”י קריטריון היציבות של נייקוויסט.

פתרון:
החוג הפתוח:

נעבוד במה שנקרא שיטת הנקודה הצפה. נגדיר:

נבדוק איפה חותך את הציר הממשי, כלומר איפה הפאזה שלו .

לכן הפאזה:

נשווה ל-, ולאחר זהויות מכוערות נקבל:

אנו מקבלים גם , אבל הוא קיים בתמונת מראה, ולכן נתעלם ממנו כרגע.
נשים לב שכאשר , מתקיים . כאשר , נקבל .

ממיקומים אלו, אנו יודעים לשרטט את עקום נייקוויסט:

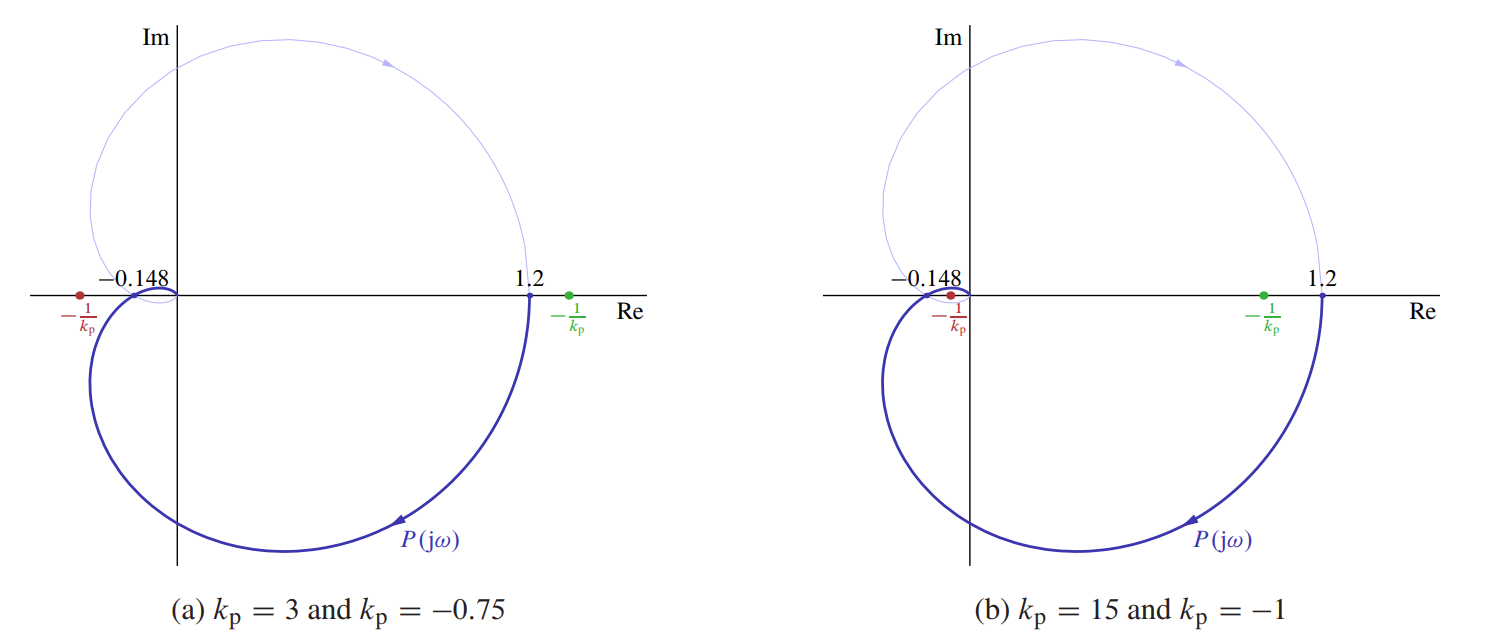
עקומות נייקוויסט עם מיקומי נקודות קריטיות שונים.

מאחר ו-, נרצה לדעת מתי . נשים לב ש:

• אם , אז , ולכן החוג הסגור יציב.
• אם , אז , ולכן החוג הסגור לא יציב.
• אם , אז , ולכן החוג הסגור לא יציב.
• אם , אז ולכן החוג הסגור יציב.

אם נסתכל במג”ש:

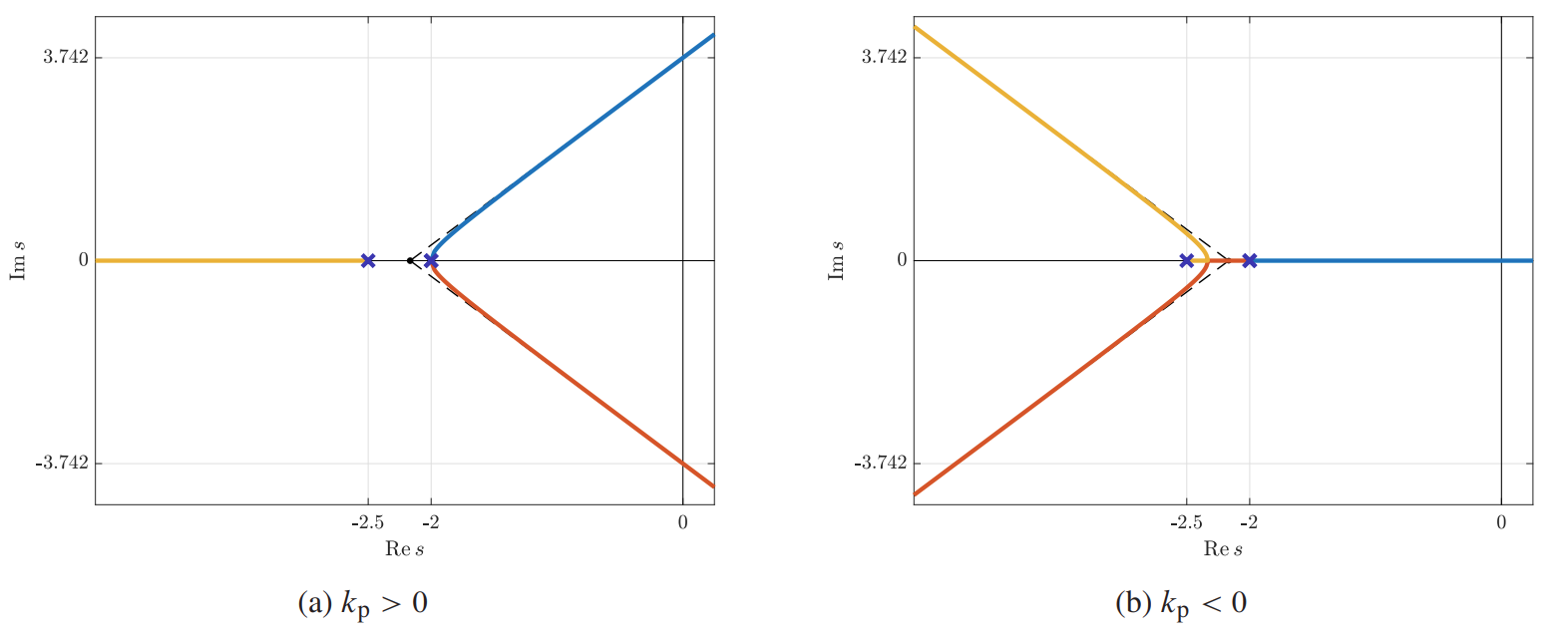
דיאגרמות מג”ש לבעיה.

תרגיל 2

התהליך

מבוקר בחוג סגור (משוב יחידה) ע”י בקר פרופורציוני , ל-. מצאו את מספר הקטבים של החוג הסגור ב-RHP כפונקציה של בעזרת קריטריון יציבות נייקוויסט.

פתרון:
נעשה את אותו התהליך. נתחיל מהפאזה:

נסיק כי האינטגרטור לא נחשב.
החיתוכים עם הציר הממשי:

לאחר עוד כמה פיתוחים מעצבנים נקבל ש:

החיתוכים מתרחשים ב:

כדי לצייר את הגרף הפולארי של כבר לא מספיק לדעת רק את נקודות חיתוך אלה - הפונקציה כבר לא מונוטונית. נצטרך קודם לבנות את הבודה שלה:

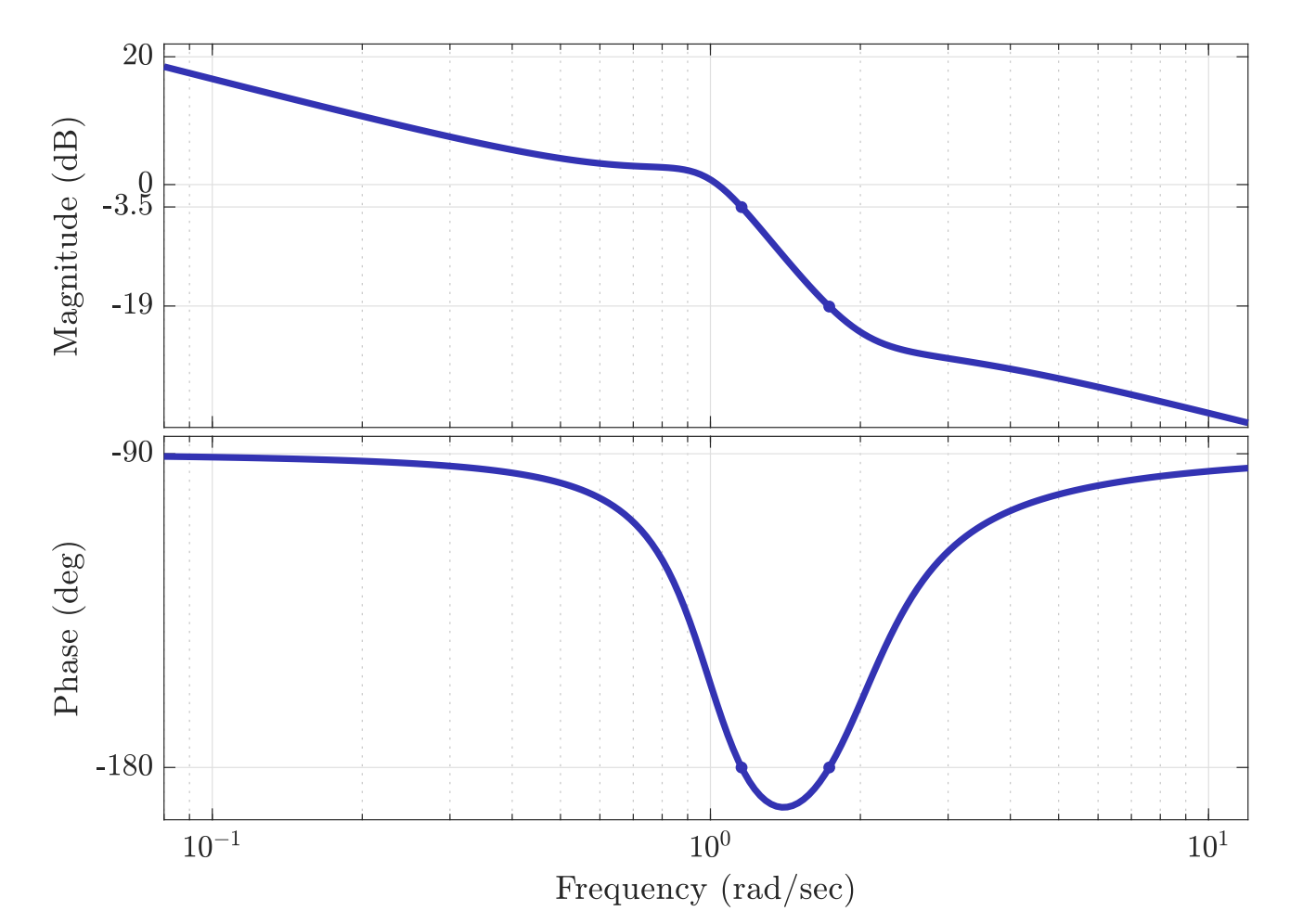
גרף בודה של .

מגרף בודה זה אנו יודעים לשרטט את הגרף הפולארי:

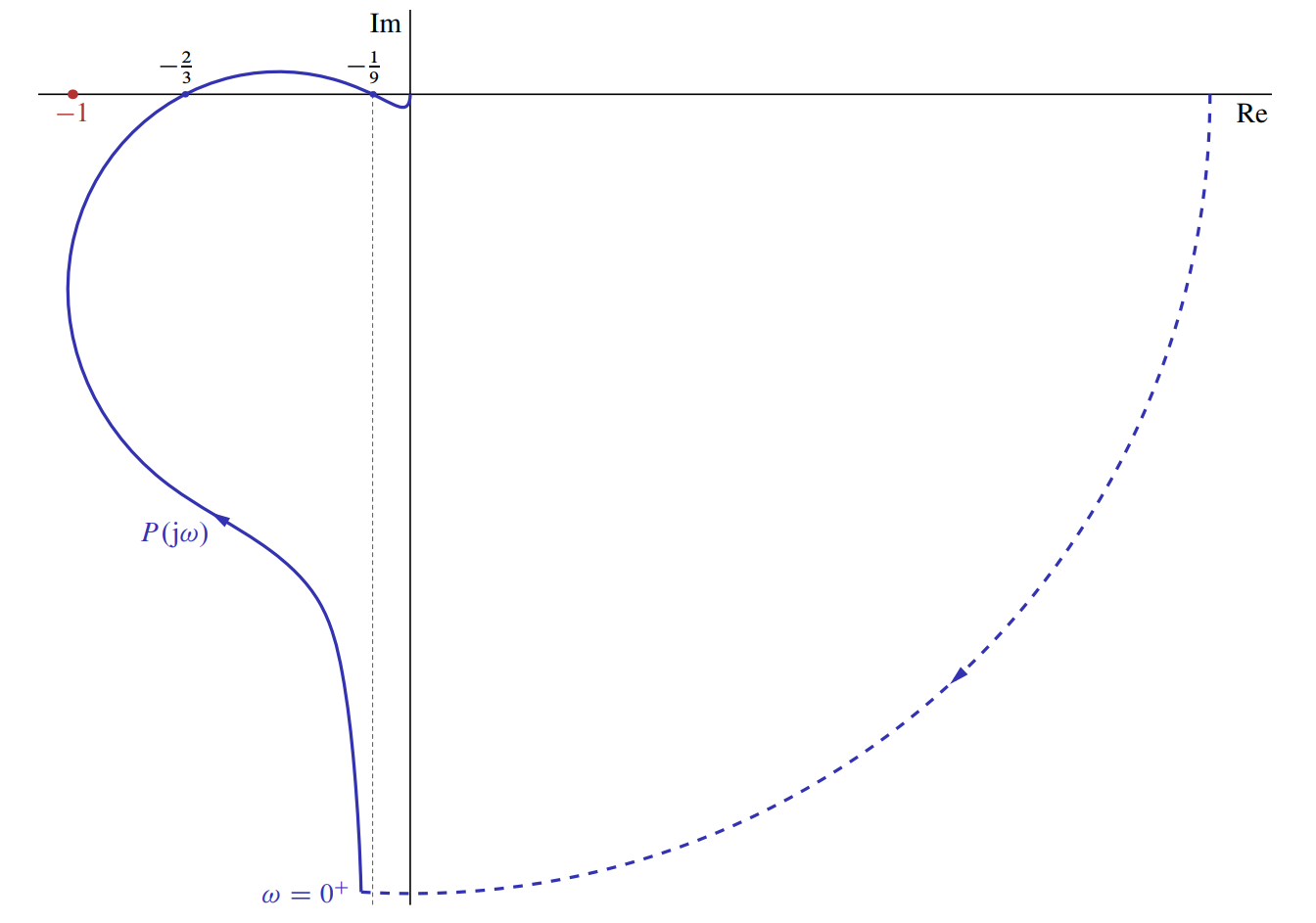
הגרף הפולארי של (ללא המראה שלו). ההשלמה שלו ברבע מעגל היא כתוצאה מהאינטגרטור.

נמצא את מספר הסיבובים לפי חיתוכים עם הקרן:

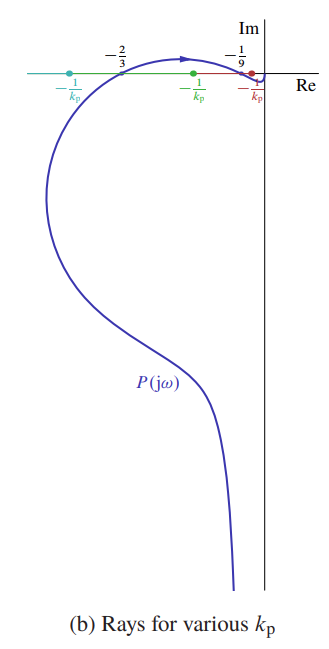
ערכי שונים.

מאחר ו-, נרצה לדעת מתי . נשים לב ש:

• אם , אז , ולכן החוג הסגור יציב.
• אם , אז , ולכן החוג הסגור לא יציב.
• אם , אז , ולכן החוג הסגור יציב.

→ קודם: ICT1_008הבא: ICT1_010 ←