IME1_002 עיבוד אותות אנלוגיים בעזרת מגברים

→ קודם: IME1_001הבא: IME1_003 ←

מבוא

מאחר ומעגלים אלקטרוניים קיימים בכל המערכות המכטרוניות, חשוב מאוד שמהנדסים יפתחו הבנה בסיסית של אותות חשמליים. לרוב אותות אלו מגיעים ממַתְמְרִים, שממירים גדלים פיזיקליים (טמפרטורה, עיבור, תזוזה, קצב זרימה) לזרמים או מתחים (לרוב מתחים). פלט המתמר לרוב מתואר כאות אנלוגי, שהוא רציף ומשתנה בזמן.

לרוב האותות מהמתמרים הם לא בצורה שאנו רוצים שהם יהיו:

• יותר מדי קטנים, לרוב בטווח ה-.
• רועשים מדי, לרוב בגלל הפרעות אלקטרומגנטיות.
• מכילים מידע לא נכון, בגלל איכות המתמר או התקנה גרועה שלו.
• בעלי הֶסֵּט DC.

רוב בעיות אלו ניתנות לתיקון ע”י עיבוד אותות אנלוגיים מתאים. אופן עיבוד האותות הכי פשוט והכי נפוץ הוא הגברה (amplification), בו עוצמת אות המתח עולה.

מגברים

נודר אתם חייבים לצפות בסרטון הבא:

אידיאלית, מגבר (amplifier) מגדיל את האמפליטודה של אות בלי שינוי הפאזה של מרכיבים שונים באות. כאשר בוחרים או מתכננים מגבר, אנו צריכים לקחת בחשבון גודל, מחיר, הספק, אימפידנס (impedance) כניסה ואימפידנס יציאה, רוחב פס והגבר.
בכללי, אנו ממדלים מגבר כמכשיר עם פתחים, כאשר מתח כניסה ויציאה מיוחסים להארקה, כפי שמיוצג באיור הבא:

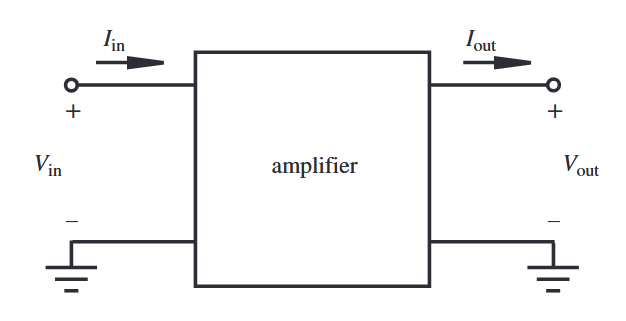
מודל מגבר. (Alciatore, 2019).

הגבר המתח של מגבר מגדיר את הקבוע בו המתח משתנה:

לרוב נרצה מגבר לינארי, כך שהוא זהה עבור כל התדרים של . אבל, ניתן לתכנן מגברים כך שיגבירו רק תדירויות מסוימות, כך שאנו בעצם מקבלים פילטר. במקרים אלו, מאפייני מתח היציאה תלויים ברוחב הפס (bandwidth) של המגבר והתדירויות קצה המתאימות.

האימפידנס כניסה של מגבר, , מוגדר כהיחס בין המתח כניסה לזרם:

רוב המגברים מתוכננים עם אימפידנס כניסה גבוה מאוד כך שמעט מאוד זרם נמשך מהכניסה.
אימפידנס היציאה הוא מדד של כמה מתח היציאה משתנה עם שינוי בזרם החיצוני:

מודל אידיאלי למגבר שרת

באיור הבא מתואר הסימון המקובל ל-מַגְבֵּר שָׁרֵת (operational amplifier). זהו מגבר שאנו מניחים שיש לו אינסוף הגבר.

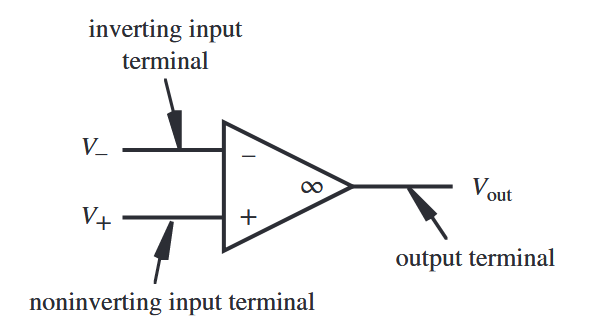
מונחי וסכמת מגבר שרת. (Alciatore, 2019).

לשתי הכניסות אנו קוראים כניסה הופכת (inverting input) המסומנת וכניסה לא-הופכת (noninverting input), המסומנת ב-. הסימון מעיד על הגבר אינסופי וההנחה שמדובר במגבר שרת אידיאלי. כל המתחים מיוחסים להארקה. המגבר שרת הוא מכשיר אקטיבי הדורש חיבור למספק כוח חיצוני, לרוב . הספק החיצוני לרוב לא מוצג בשרטוטים. כיוון שהמגבר שרת הוא מכשיר אקטיבי, מתחי וזרמי היציאה יכולים להיות גדולים יותר מהאותות כניסה.

כפי שמוצג באיור הבא, מגבר שרת לרוב יכלול משוב בחזרה לכניסה הופכת, מה שהופך אותו למערכת בחוג סגור.

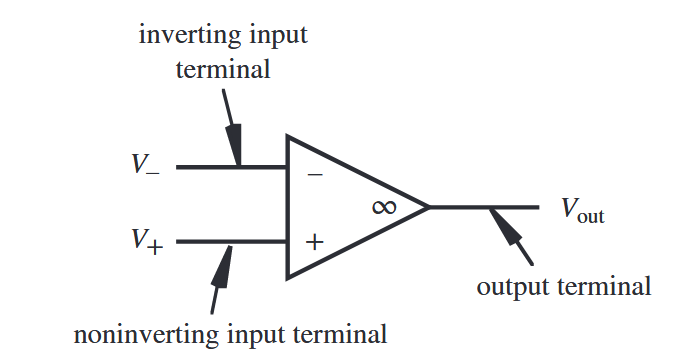
משוב מגבר שרת. (Alciatore, 2019).

מגבר בחוג סגור הרבה יותר יציב ממגבר ללא משוב, הנקרא מגבר בחוג פתוח, ולכן הוא הנפוץ יותר.

האיור הבא מתאר מודל אידיאלי שיכול לעזור בניתוח מעגלים הכוללים מגברי שרת:

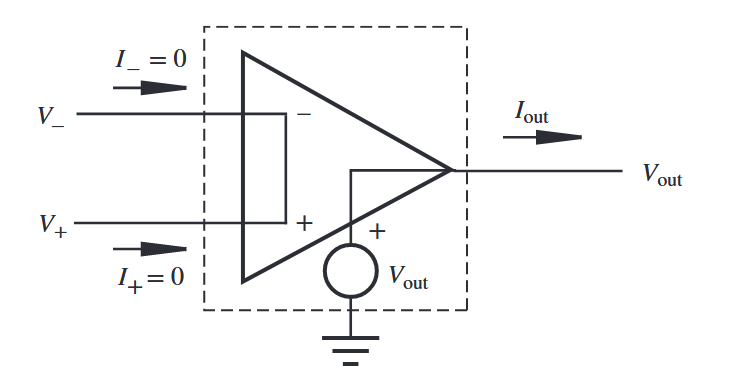
מעגל שקול למגבר שרת. (Alciatore, 2019).

המודל מתבסס על ההנחות הבאות שמתארות מגבר שרת אידיאלי:

• יש לו אימפידנס אינסופי בכניסה וביציאה, כך שהוא לא צורך זרם מהכניסות:
• יש לו הגבר אינסופי. לכן, ההפרש בין המתחי כניסה הוא אפס; אחרת היציאה תהיה אינסופית. זה מסומן באיור כקצר בין שתי הכניסות: למרות שאנו מניחים שיש קצר בין שתי הכניסות, אנו מניחים שאין זרם הזורם דרך קצר זה.
• יש לו אימפידנס יציאה אפסי. לכן, המתח יציאה לא משתנה כתוצאה מהזרם יציאה.

הנחות אלו עלולות להישמע מבלבלות ולא הגיוניות, אבל הם מספקות קירוב די טוב להתנהגות מגבר שרת אמיתי שכולל משוב. בעזרת מודל זה, אנו צריכים רק את חוקי קירכהוף וחוק אוהם כדי לנתח מעגלי מגבר שרת.

מעגלים שימושיים עם מגברי שרת

מגבר הופך סימן

מגבר הופך סימן (inverting amp) בנוי מחיבור שני נגדים חיצוניים למגבר שרת כפי שמוצג באיור הבא:

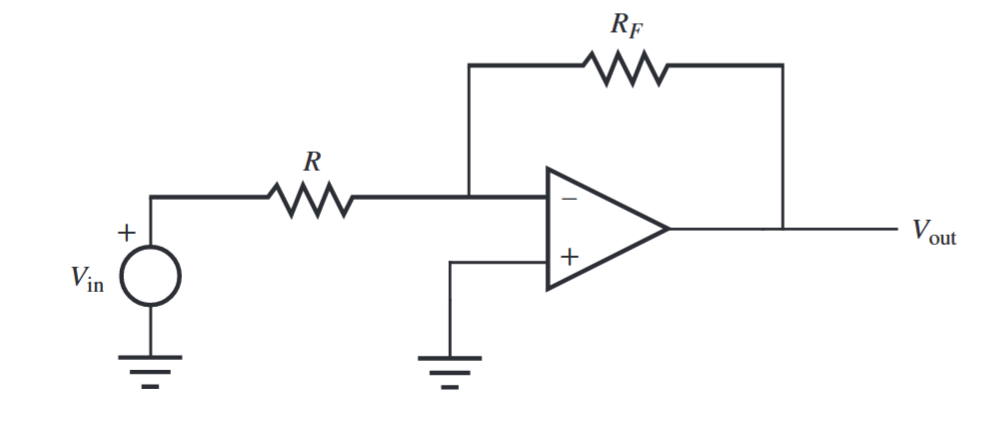
מגבר מחליף סימן. (Alciatore, 2019).

ההדק של מחובר לאדמה ולכן ’ כך שלפי מודל אידיאלי למגבר שרת, מתקיים . לפי המודל האידיאלי, המגבר לא צורך זרם בכניסה וביציאה, כך ש- , והזרם יזרום רק דרך ענף אחד המחבר בין ל-.

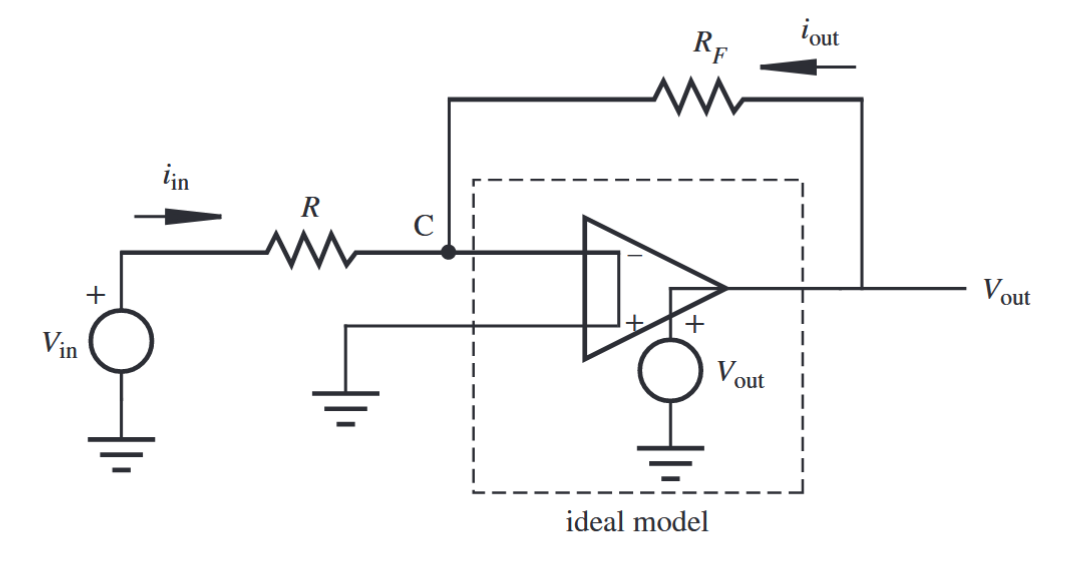
מעגל שקול למגבר מחליף סימן. (Alciatore, 2019).

אם נרשום KCL על הצומת :

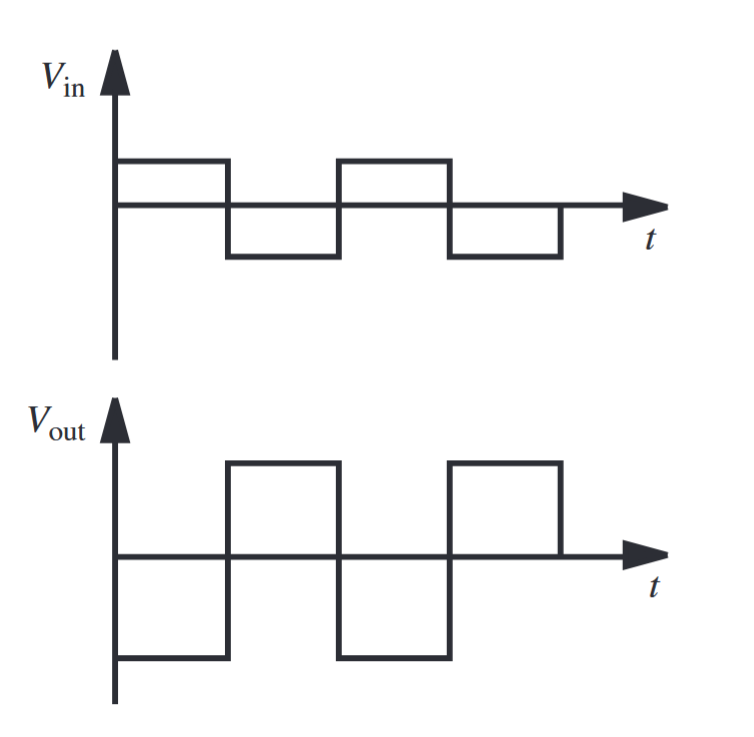
הדגמת החלפת הסימן על אות מתח כניסה . (Alciatore, 2019).

מגבר שומר סימן

סכמת מגבר שומר סימן (non-inverting amp) מוצגת באיור הבא:

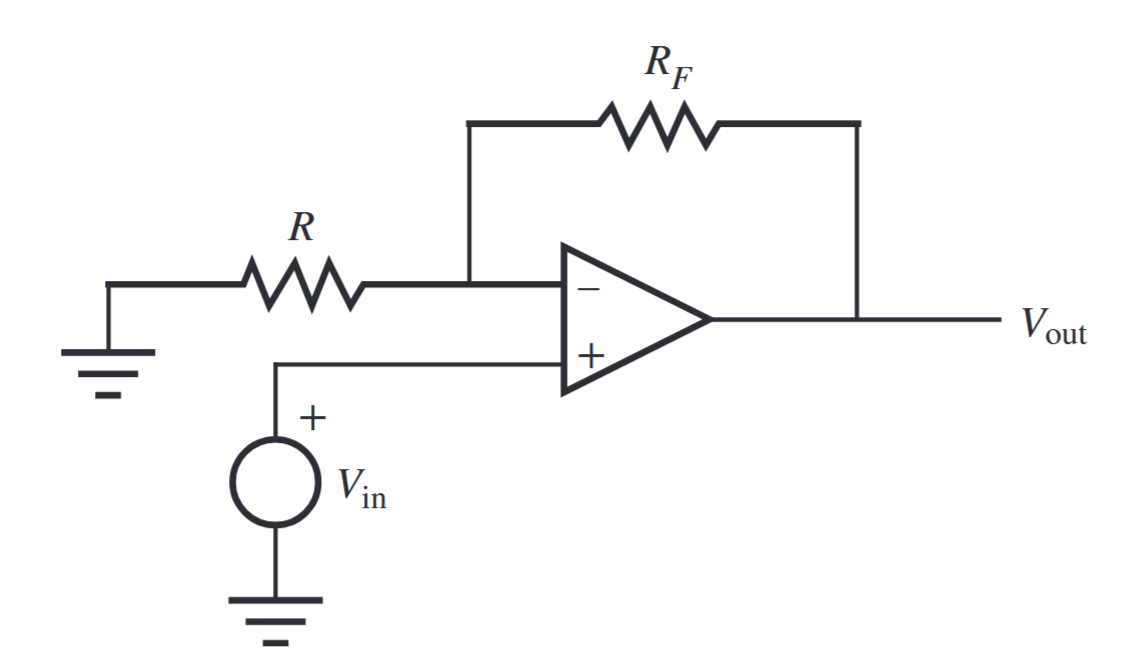
מגבר שומר סימן. (Alciatore, 2019).

במעגל הזה ולכן נוכל לומר ש- . גם כאן זרם אינו נכנס למגבר ולכן קיים רק ענף אחד בו זורם זרם: מ- ל-.

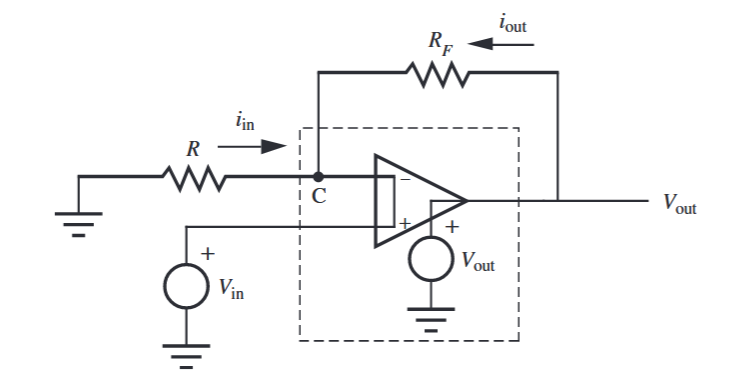
מעגל שקול למגבר שומר סימן. (Alciatore, 2019).

לפי KCL על :

אם וגם במגבר השומר סימן באיור לעיל, נוכל לתאר את המערכת פשוט ע”י:

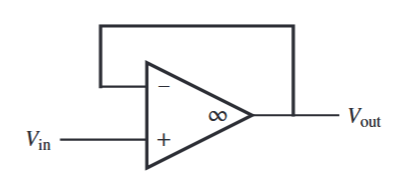
מגבר חוצץ - buffer. מ-(Alciatore, 2019).

למגבר מסוג זה קוראים חוצץ (buffer, follower), כי . יש לו אימפידנס כניסה גבוה ואימפידנס יציאה נמוך. מעגל זה שימושי אם אנו רוצים לעקוב (להעתיק) אות מתח בלי להעמיס את מקור המתח של אות הכניסה - העומס האמיתי נופל על מקור המתח של המגבר. האימפידנס הגבוה בכניסה למעשה מבודד את המקור משאר המערכת.

מגבר מסכם ומחסיר מתח

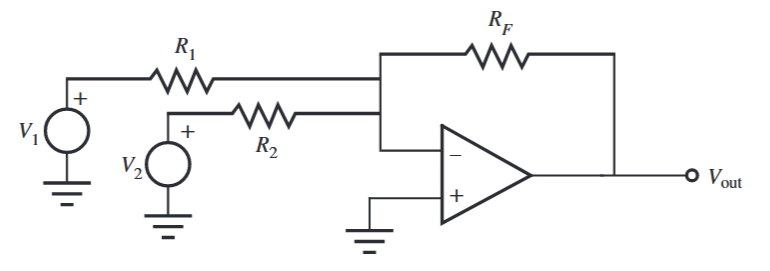
מעגל מסכם מתח. (Alciatore, 2019).

מעגל מסכם מתח (summer) המוצג לעיל פשוט סוכם מתחים. מניתוח המערכת ניתן להראות ש:

לכן, פלט המערכת הוא הסכום השלילי של הכניסות, בשקלול ההתנגדות המתאימה.

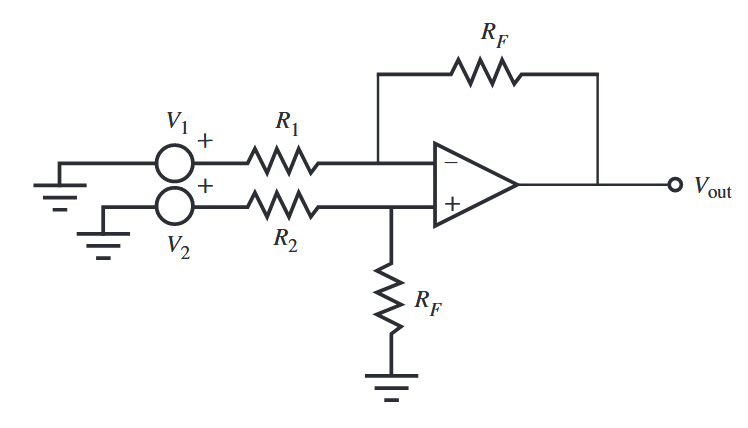
מעגל מחסיר מתח. (Alciatore, 2019).

מבחינת מחסר מתח (difference amp) המוצג לעיל, ניתן להראות בעזרת סופרפוזיציה שאם :

מעגל משווה

נוכל להיעזר במעגל משווה (comparator) כדי למצוא אם אות אחד יותר גדול מאות אחר. המשווה הוא דוגמה למגבר שרת שבו אין משוב, ולכן למערכת הגבר אינסופי.

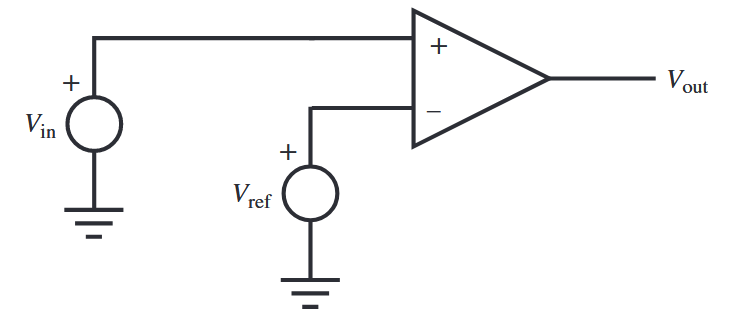
מגבר משווה.

התוצאה היא שמגבר השרת רווי (saturates) - המתח ביציאה נשאר בערכו הכי גבוה או הכי נמוך :

מעגל אינטגרטור

אם נחליף את הנגד משוב של מגבר הופך סימן בקבל, התוצאה היא אינטגרטור:

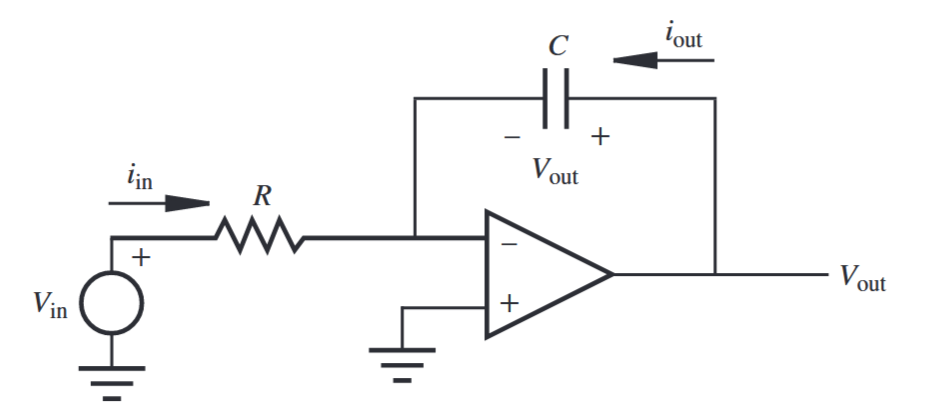
אינטגרטור אידיאלי. (Alciatore, 2019).

נשים לב שהקשר בין המתח והזרם בקבל הוא:

מאינטגרציה נקבל:

מאחר ו- וגם :

חייבים לזכור כי חסום בין מתח ההספקה ולכן, כאשר יגיע למתח הזה, ערכו יישאר קבוע. לאינטגרטור מסוג זה יש הגבלה פיזיקלית והיא הרוויה אשר תלויה במתח ההספקה.

דוגמה:

נתון האינטגרטור הבא:

כאשר מתח הכניסה הוא:

דרוש למצוא את מתח היציאה .

פתרון:
האינטגרטור מבצע אינטגרל על הפונקציה ולכן בכל פעם שהפונקציה מתאפסת:

וכאשר הפונקציה מקבלת ערך של :

לכן האות ביציאה ייראה כך:

אינטגרטור יותר פרקטי הוא ה-low-pass filter:

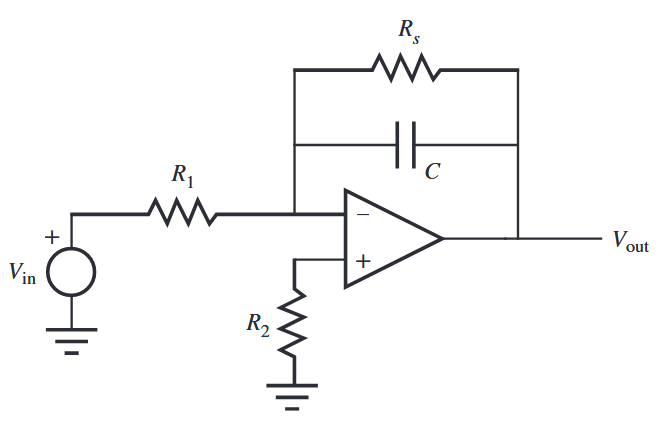
Low-pass filter. (Alciatore, 2019).

הנגד המחובר במקביל לקבל נקרא נגד דלף/מֵצַד (shunt resistor). מטרתו היא להגביל את ההגבר בתדר נמוך של המעגל. זה נחוץ כי כל הזזה קטנה בכניסת DC של הכניסה תעבור אינטגרציה לאורך הזמן, מה שלבסוף ירווה את המגבר שרת.

ככל אצבע:

נבחר את להיות גדול יותר מ-.

בגלל האימפידנס והתגובת תדירות של המעגל משוב המכיל את ו-, המערכת לעיל מתפקדת כאינטגרטור רק עבור טווח תדרים מסוים. בתדרים מאוד נמוכים, המעגל מתפקד כמגבר מחליף סימן כי האימפידנס של כל המשוב הוא למעשה כי האימפידנס של גבוה בתדרים נמוכים. בתדרים מאוד גבוהים (), היציאה מוחלשת לאפס כי כעת ה- הוא low-pass filter.

מעגל גוזר

אם נגד הכניסה של מגבר מחליף סימן מוחלף בקבל, התוצאה היא מעגל גוזר (differentiator circuit).

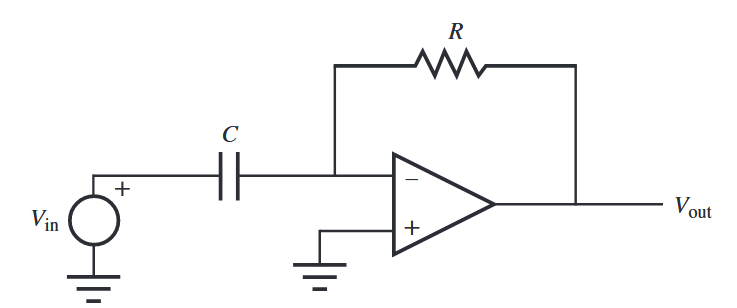
מעגל גוזר. (Alciatore, 2019).

כעת, הקשר בין המתח והזרם לקבל:

מאחר ו- וגם :

ראוי לציין כי מערכת מסוג זה אינה סיבתית והנגזרת תהיה רק לפי הגבול האחורי:

בעיה אחת של מעגלים גוזרים היא שפעולת הגזירה בכניסה תגדיל משמעותית כל רעש בכניסה - היא מגבירה את הרעש ש-משתנה מאוד מהר. לאינטגרטור לעומת זאת מחליק את הכניסה.

תרגילים

תרגיל 1

נתון המעגל:

סכימת המעגל.

צומת מחוברת לנגד משתנה של והמתח בצומת יכול להשתנות בצורה רציפה מ- עד וולט.

סעיף א’

חשב את המתח בצומת כפונקציה של ו-.

פתרון:
נשרטט מעגל חשמלי שקול לחיבור התחתון ב- (נשים לב שהמתח ב- הוא אפס כי ):

מעגל שקול לטובת החישוב המתח ב-.

ההתנגדות השקולה:

לכן הזרם:

והמתח על ועל (שהוא המתח בצומת ) יהיה:

נקבל:

סעיף ב’

מה צריך להיות ערך הנגדים ו- כך שהמצח בצומת יהיה ?

פתרון:
נציב:

אנו גם יודעים מהנתון ש:

מפתרון מערכת משוואות זו נקבל פתרון פיזיקלי יחיד:

סעיף ג’

עבור נתון כפרמטר, מצאו את כפונקציה של .

פתרון:
נשים לב שהמגבר הנתון הוא מגבר מסכם ומחסיר מתח. לכן:

תרגיל 2

נתון המעגל הבא:

סכמת המעגל.

סעיף א’

יש למצוא את הגבר המעגל.

פתרון:
נשים לב ש:

תחת הנחות מגבר אידיאלי, . כך ש:

בנוסף, מחוק אוהם:

כך שהמתח על :

נציב בביטוי עבור :

סעיף ב’

מצאו את הזרם ב- כפונקציה של .

פתרון:
מסעיף קודם:

נשים לב ש:

נקבל:

תרגיל 3

נתון המעגל הבא, כאשר מתח האספקה של המגבר הוא .

סכמת הבעיה.

נתונים:

סעיף א’

יש למצוא את הזרם ב-.

פתרון:
תחת הנחת מגבר אידיאלי, אין זרם דרך הנגד ולכן . ע”פ אותה ההנחה נקבל כי גם . כלומר, המתח שנופל על הוא ולכן הזרם בו הוא .

סעיף ב’

יש למצוא את הזרם ב-.

פתרון:
מאחר ו- , נקבל כי המתח על . לכן, הזרם ב- הוא:

מאחר ולא נכנס זרם למגבר נקבל כי הזרם ב- זהה.

סעיף ג’

יש למצוא את הגבר המעגל ומתח המוצא.

פתרון:
ע”פ התוצאה של סעיף קודם נקבל כי:

נוכל להציב ב:

מאחר ומתח הכניסה הוא נקבל כי ההגבר הוא .

→ קודם: IME1_001הבא: IME1_003 ←