IRB1_002 Forward Kinematics

← Previous: IRB1_001Next: IRB1_003 →

from (Lynch & Park, 2017):

Forward Kinematics

The forward kinematics of a robot refers to the calculation of the position and orientation of its end-effector frame from its joint coordinates . The following figure illustrates the forward kinematics problem for a planar open chain.

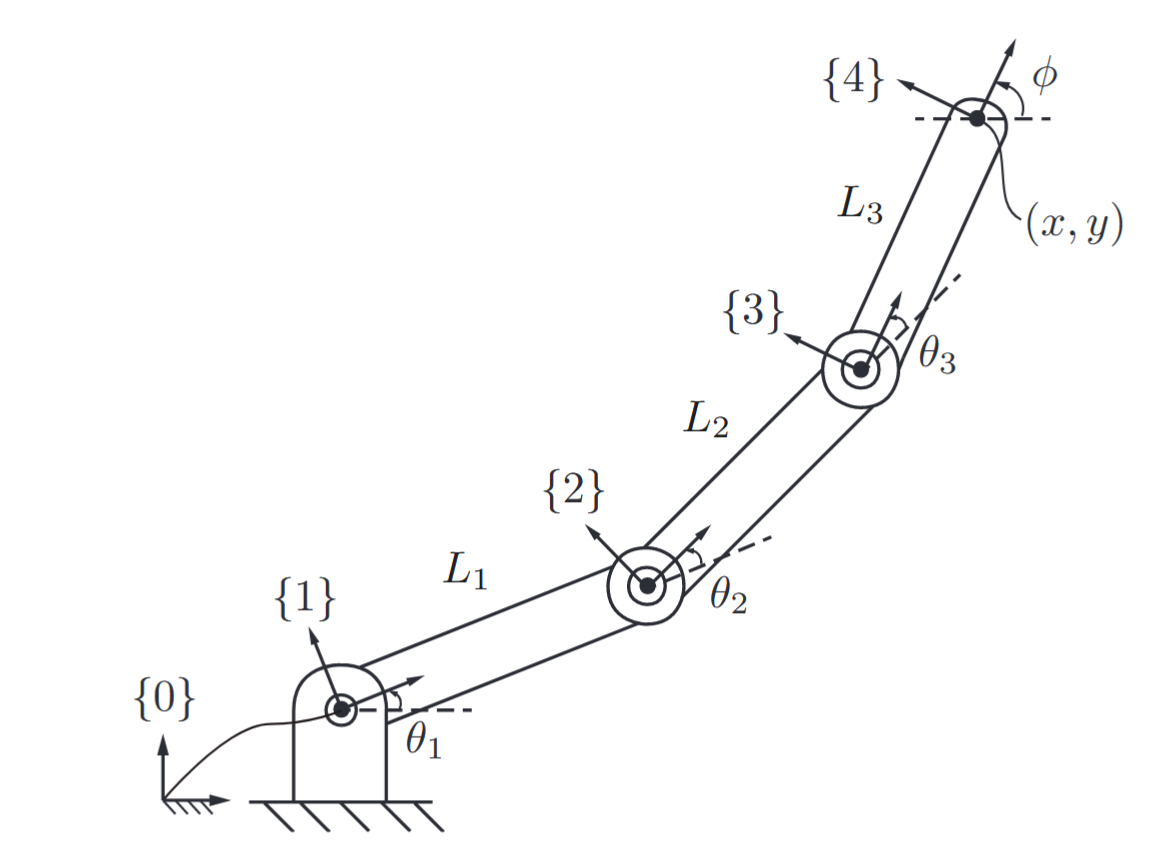
Forward kinematics of a planar open chain. For each frame, the and is shown; the -axes are parallel and out of the page. (Lynch & Park, 2017).

The link lengths are , , and . Choose a fixed frame with origin located at the base joint as shown, and assume an end-effector frame has been attached to the tip of the third link. The Cartesian position and orientation of the end-effector frame as functions of the joint angles are then given by

A more systematic method of deriving the forward kinematics might involve attaching reference frames to each link

where

Assigning Link Frames

One widely used representation for the forward kinematics of open chains relies on the Denavit–Hartenberg parameters (D–H parameters), and this representation uses equation (LP4.4).

The basic idea underlying the Denavit–Hartenberg approach to forward kinematics is to attach reference frames to each link of the open chain and then to derive the forward kinematics from the knowledge of the relative displacements between adjacent link frames.

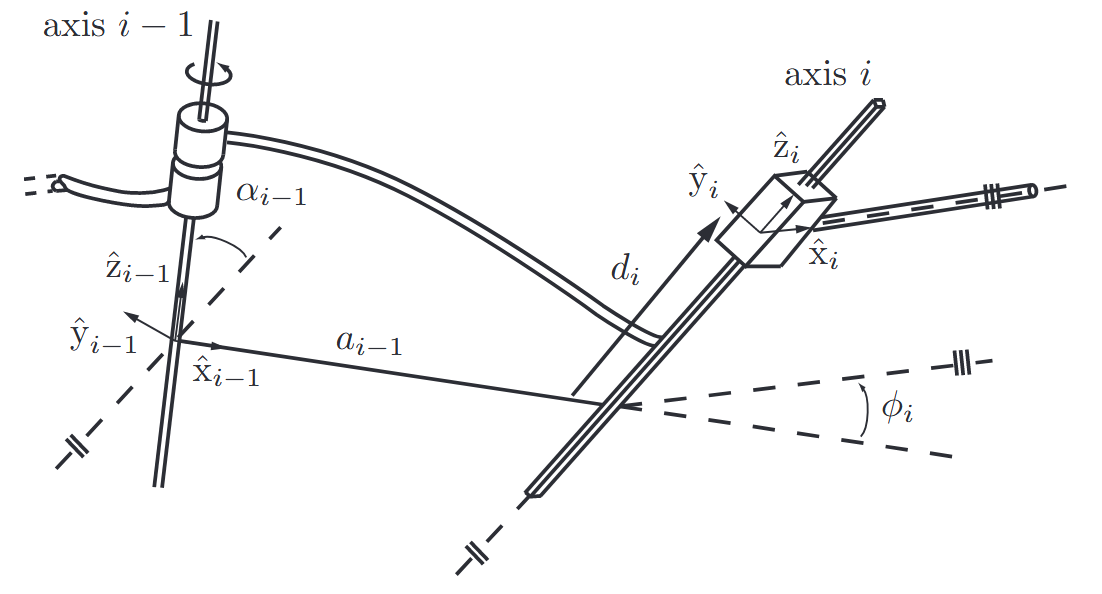
Rather than attaching reference frames to each link in an arbitrary fashion, in the Denavit–Hartenberg convention a set of rules for assigning link frames is observed. The following figure illustrates the frame assignment convention for two adjacent revolute joints and that are connected by link .

Illustration of the Denavit–Hartenberg parameters. (Lynch & Park, 2017).

The first principle in assigning reference frames is that the axis should align with the axis of joint , while the axis aligns with joint . The direction of positive rotation around each link’s -axis is determined using the right-hand rule.

Once the direction of the -axis is established, the next step is to determine the origin of the reference frame for the link. This is done by identifying the line segment that intersects both and at right angles. For now, we assume this line is unique. (Special cases, like parallel axes—where the line isn’t unique—or intersecting axes—where no perpendicular exists—are discussed later.)

The origin of frame is placed at the point where this perpendicular line intersects joint axis .

With the origin defined, the remaining axes of the frame follow naturally:

• The -axis is oriented along the direction of the perpendicular line, pointing from axis to axis .
• The -axis is then defined by the cross product , in accordance with the right-hand rule.

The figure above shows the resulting frames and .

With the frames defined, we now introduce four parameters that fully describe the transformation :

• Link twist : The angle between and , measured about .
• Link length : The length of the perpendicular line between axes and .

  Note:

  Despite the name, this does not necessarily represent the actual physical length of the link.

• Link offset : The distance from to along
• Joint angle : The angle from to , measured around the -axis.

These four parameters are known collectively as the Denavit–Hartenberg parameters. For an open-chain robotic arm with one-degree-of-freedom joints, a total of D–H parameters fully define the forward kinematics.

If all joints are revolute:

• The parameters , , and are constants.
• The joint angle serves as the joint variable.

We will now address:

• Cases where the perpendicular line is undefined or not unique.
• Scenarios with prismatic joints.
• Guidelines for selecting the ground and end-effector frames.

When Adjacent Revolute Joint Axes Intersect

If two consecutive revolute joint axes intersect, then no single line exists that is perpendicular to both axes. In such situations, we assign the link length , and define the axis as being perpendicular to the plane formed by and .

This setup yields two valid options: one that results in a positive link twist angle and another that gives a negative value. Both are acceptable; the choice depends on consistency and convention.

When Adjacent Revolute Joint Axes Are Parallel

Another special case arises when two adjacent revolute joint axes are parallel. Here, infinitely many perpendicular lines can be drawn between the axes (technically, a one-dimensional family of such lines exists), and any of them can be used to define the frame.

The general recommendation is to pick the perpendicular line that feels most physically meaningful and simplifies the D–H parameters—ideally resulting in more zeros.

Prismatic Joints

For prismatic joints, the -axis of the link frame is aligned with the direction of positive translation. This mirrors the convention used for revolute joints, where defines the axis of positive rotation.

Under this convention:

• The link offset becomes the joint variable.
• The joint angle is fixed.

The method for setting the origin and determining the and axes remains unchanged from the revolute joint case. See the following figure for illustration:

Link frame assignment convention for prismatic joints. Joint is a revolute joint, while joint is a prismatic joint. (Lynch & Park, 2017).

Choosing the Ground and End-Effector Frames

So far, we’ve discussed how to assign link frames, but not how to define the ground (base) frame or the final end-effector frame. A helpful strategy is to choose these in a way that feels intuitive and results in the simplest possible D–H parameter set.

Typically:

• The ground frame is placed to coincide with frame when the system is in its zero (home) configuration.
• For a revolute joint, this leads to .
• For a prismatic joint, we get .
• The end-effector frame is positioned at a convenient reference point on the tool or device, chosen for clarity in task description and simplification of D–H parameters (ideally making them zero where possible).

Keep in mind, though, that not all arbitrary frame choices will work—there may be no valid set of D–H parameters that describe the transformation if the initial or final frames are chosen inconsistently. This point will be addressed in further detail.

Manipulator Forward Kinematics

Once all the transformations , between adjacent link frames are known in terms of their D–H parameters, the forward kinematics is obtained by sequentially multiplying these link transformations. Each link frame transformation is of the form

Exercises

Note:

We prefer using the shorthand

which means, using trigonometric identities,

Question 1

Given the robot shown in the figure below:

Simple robot with one revolute and one prismatic joint.

Compute the last transformation .

Solution:
First, let’s assign link frames.

Assigning link frames.

We need to establish our coordinate frames according to the D–H parameters.

We will compute each transformation matrix using the D–H parameters from the table.

For each joint, the transformation matrix is:

Computing each individual transformation matrix:

Therefore the last transformation:

Question 2

Compute the forward kinematics of the following manipulator:

A manipulator with 2 revolute and 1 prismatic joints.

Solution:
First, we’ll mark the axes.

Marking axes along the joints’ axes.

Now we can complete the other frames, starting from the world frame:

Assigning all the frames according to the convention.

Now to plot all the parameters in a table:

The forward kinematics will then be:

← Previous: IRB1_001Next: IRB1_003 →