LSY1_011 Fourier Analysis of Discrete Time Signals

← Previous: LSY1_010

Introduction

From (Lathi & Green, 2018):
In Fourier transform and Laplace transform we studies the ways of representing a continuous-time signal as a sum of sinusoids or exponentials. In this chapter we shall discuss similar development for discrete-time signals. Our approach is parallel to that used for a continous-time signals. We first represent a periodic as a Fourier series formed by a discrete-time exponential (or sinusoid) and its harmonics.

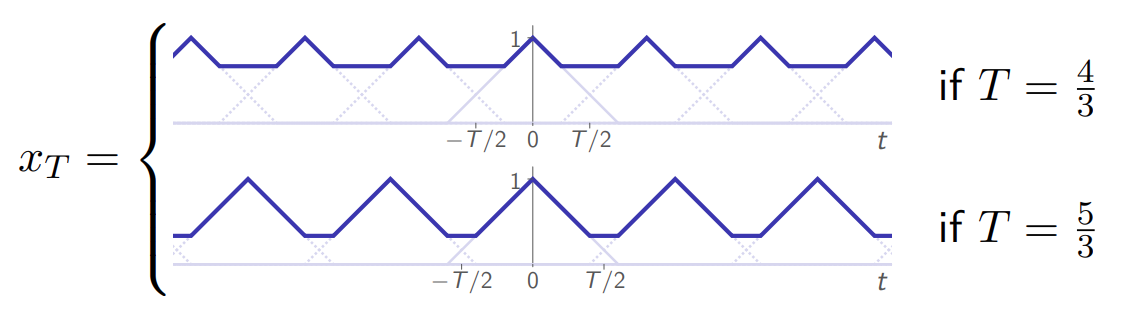
The signal , for and is called a discrete harmonic signal with frequency , amplitude , and initial phase :

A general discrete harmonic signal.

A/D and D/A Conversion

Analog to Digital

A conversion of a continuous-time (analog) signal, say , to a discrete-time (digital) signal, say , is known as sampling. If for all

then the term ideal sampling is used. If for some , we say that the sampling is periodic and call the sampling period/interval.

Sampling frequently (but not always) a lossy process, meaning some information about the analog signal is lost. For example:

Information loss on an analog signal.

Digital to Analog

A conversion of a discrete-time (digital) signal, say , to a continuous-time (analog) signal, say , is known a hold (interpolation). We will mainly deal with zero-order hold, which acts as:

For example:

Discrete-Time Fourier Transform

Definition:

A discrete-time Fourier transform (DTFT) is defined as

under some mild conditions, the inverse discrete-time Fourier transform results in:

Symbolically:

Basic Properties

property	time domain	frequency domain
linearity
time shift
time reversal
conjugation
modulation
convolution

Periodic Summation

The ideal sampler maps continuous-time signals to discrete signals as

for a given sampling period (we assume periodic sampling hereafter). We may also think in terms of the sampling frequency .

A key question: What is lost by transforming the signal domain from to ?

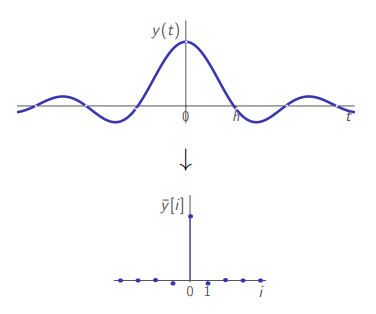
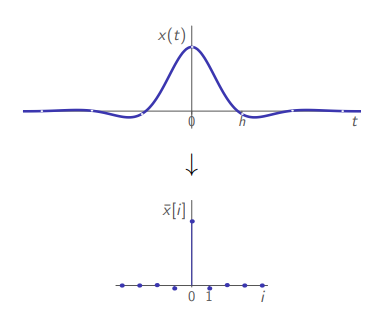
Sampling with a general sampling period h.

Sampling with a general sampling period . We got that exact same sampled function even though the original continuous-time function isn’t the same.

SmarterEveryDay loosing his kids in a science museum

Washing machine dude explaining signals

Definition:

Consider a function . Its periodic summation with period is:

Note:

The function is -periodic.

Example:

If , then:

Let be a continuous-time signal with the frequency response , say:

Frequency response .

And consider its periodic summation with the period :

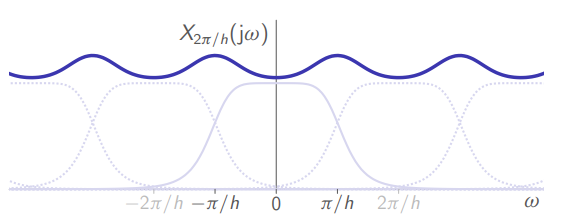
Periodic summation .

Because this function is periodic, it can be expanded into a Fourier series with fundamental frequency . After some algebra, we conclude that the Fourier coefficients are:

Meaning that the periodic summation can also be described as the sum:

At the same time, the DTFT of (where ) satisfies

Hence, the DTFT of the sampled signal satisfies

Which is the periodic summation, whose period equals the sampling frequency , of the spectrum of the continuous-time , scaled by the factor both in amplitude and in frequency.

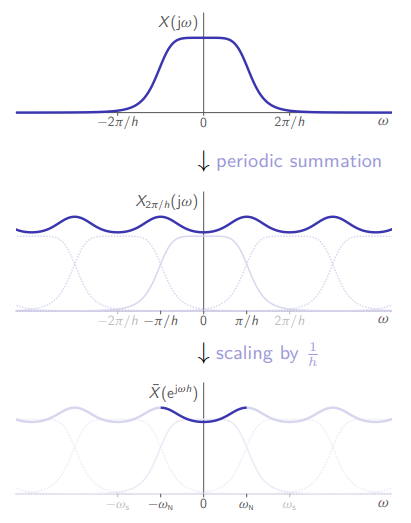
Method of finding .

Meaning that spectrum of a sampled signal will always be periodic. Because it is periodic, we usually focus on the range , where :

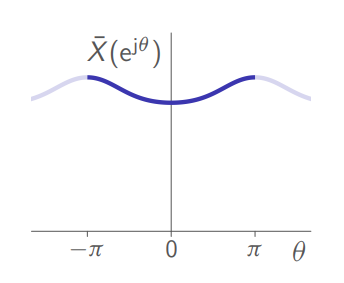
Change of variables for convenience.

Note:

This periodic spectrum is not a action we are doing to better understand they system, it is a thing that happens, a phenomenon called aliasing, which is a result of the fact that the sampling rate we are using is too slow to capture all the data we need.

We define the Nyquist frequency , where we can think of it as the frequency at which the spectrum of the original signal “folds” upon:

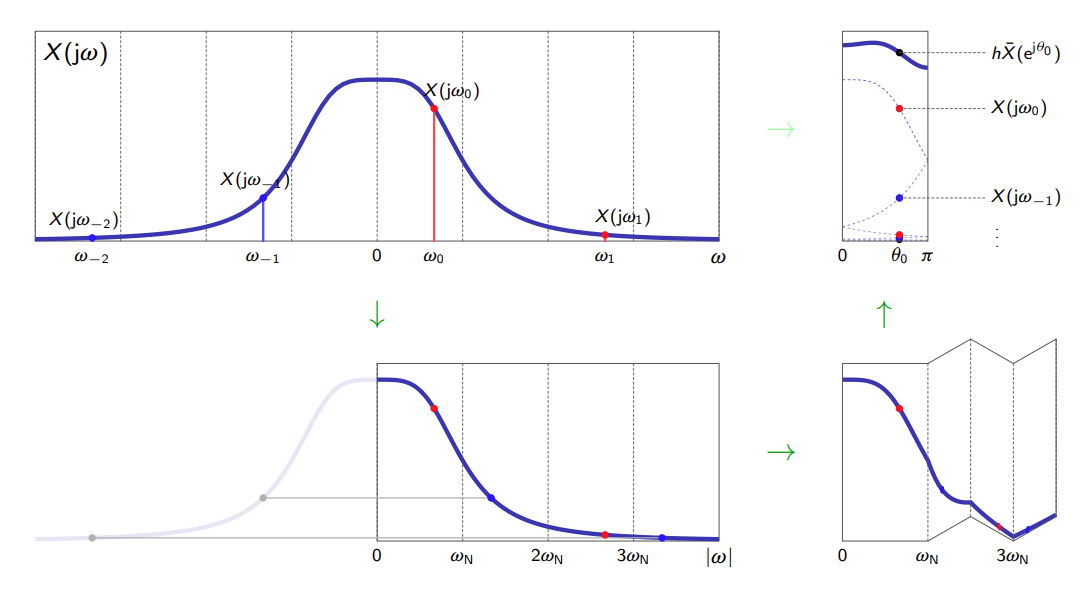
Demonstration of frequency folding.

Exercises

Question 1

Let , i.e:

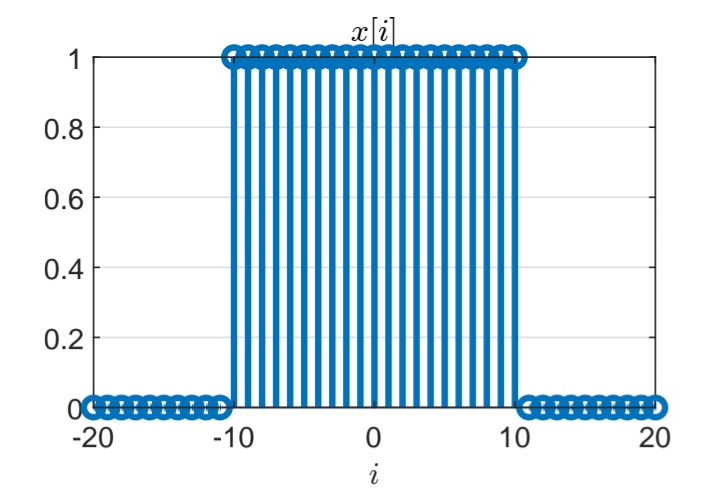
Discrete-time signal , for .

Solution:
We can write as a sum of shifted step signals 𝟙:

𝟙𝟙

We know that:

𝟙

also the time shift property of the DTFT:

Using these we have:

Using the sifting property of the delta function, we know that . Therefore:

Multiplying the numerator and denominator by :

To conclude:

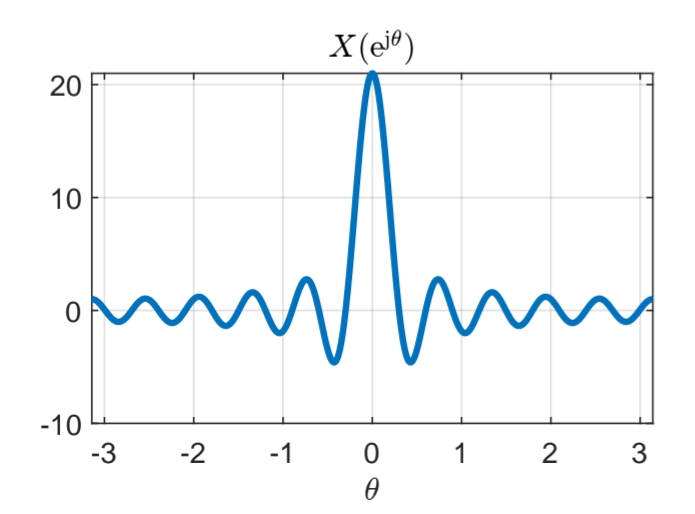
The plot of for .

← Previous: LSY1_010