LSY1_008 Fourier Transform

← Previous: LSY1_007Next: LSY1_009 →

Introduction

From (Lathi & Green, 2018):
Electrical engineers instinctively think of signals in terms of their frequency spectra and think of systems in terms of their frequency response. Most teenagers know about the audible portion of audio signals having a bandwidth of about 20 kHz and the need for good-quality speakers to respond up to 20 kHz. This is basically thinking in the frequency domain.
In the following chapter we discuss spectral representation of signals, where signals are expressed as a sum of sinusoids or exponentials. Actually, we touched on this topic in the previous chapter. Recall that the Laplace transform of a continuous-time signal is its spectral representation in terms of exponentials (or sinusoids) of complex frequencies. However, in the earlier chapters we were concerned mainly with system representation; the spectral representation of signals was incidental to the system analysis. Spectral analysis of signals is an important topic in its own right, and now we turn to this subject.
In this chapter we show that a periodic signal can be represented as a sum of sinusoids (or exponentials) of various frequencies.

Fourier Series

A periodic signal with period has the property

for all . The smallest values of that satisfies this periodicity condition is the fundamental period of .

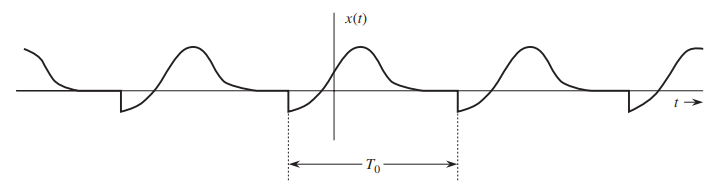
A periodic signal of period

It can be shown that:

Theorem:

If is -periodic and continuous, then we can decompose it into a Fourier series

where

and

are known as the Fourier coefficients of and is known as its fundamental frequency.

The expansion

means that every -periodic is a linear combination of elementary harmonics

whose frequencies are multiples of the fundamental frequency .
A -periodic and be equivalently represented by , known as the frequency-domain representation of .

Fourier Transform

Definition:

For a signal , its Fourier transform is defined by

Under some mild conditions, the inverse Fourier transform is

where is a constant chosen to ensure the convergence of the integral.

Symbolically:

Basic Properties

property	time domain	frequency domain
linearity
duality
time shift
time scaling
conjugation
modulation
differentiation
convolution

The Dirac Delta Property

if , then by the sifting property:

i.e. contains all elementary harmonics .

There are several consequences to this property:

• if , then by duality and evenness of :
• by modulation, if , then:
• by linearity, if , then:

Exercises

Question 1

Consider the signal defined as

Part a

Identify the period and the fundamental frequency .

Solution:
The period of is simply . Since the given signal is taken in its absolute:

The fundamental frequency is therefore:

Part b

Decompose this signal into its Fourier series.

Solution:
By its definition:

Notice that the function inside the modulus () is positive when .
Because the given signal is periodic, we can shift it by , and still get the same integral

thus ridding us of the modulus ().

Using euler’s formula:

since :

Because :

Therefore:

Since , by Euler’s formula:

Therefore:

To conclude:

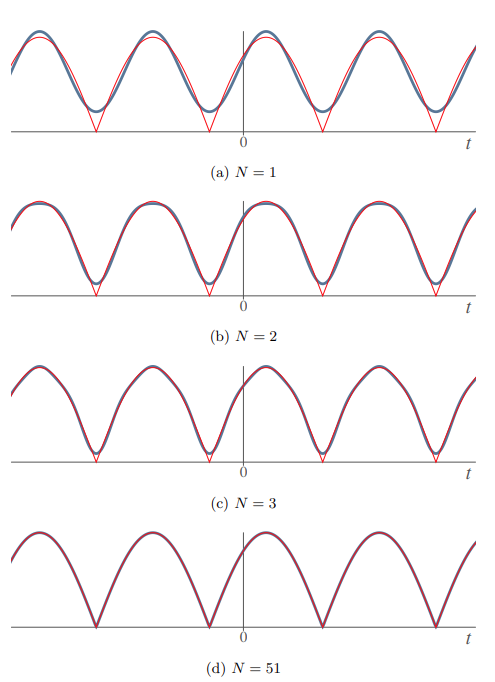
Partial Fourier series -

Part c

Apply the Fourier transform to this signal.

Solution:
We know that can be represented as a sum of its Fourier series . Therefore:

By the linearity of the Fourier transform;

By the dirac delta property:

Using the answer for the previous part, we see that:

Therefore:

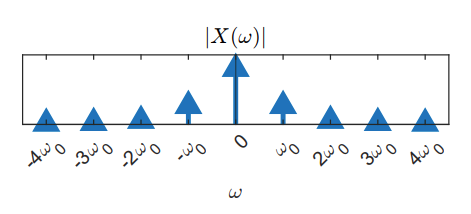
The Fourier spectrum

Question 2

Match the signals in the time domain to their corresponding magnitude Fourier spectrum:

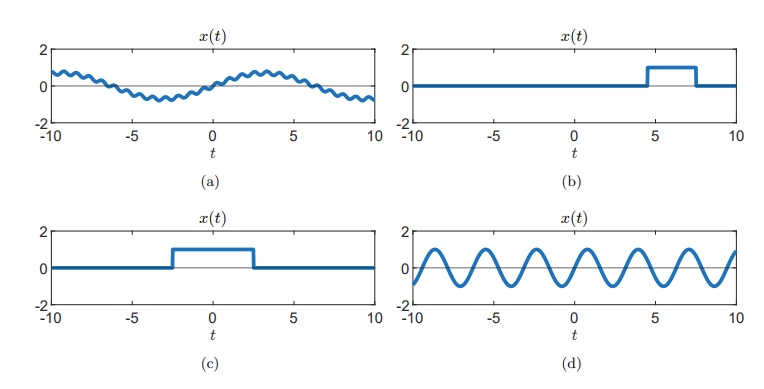
Signals in the time domain.

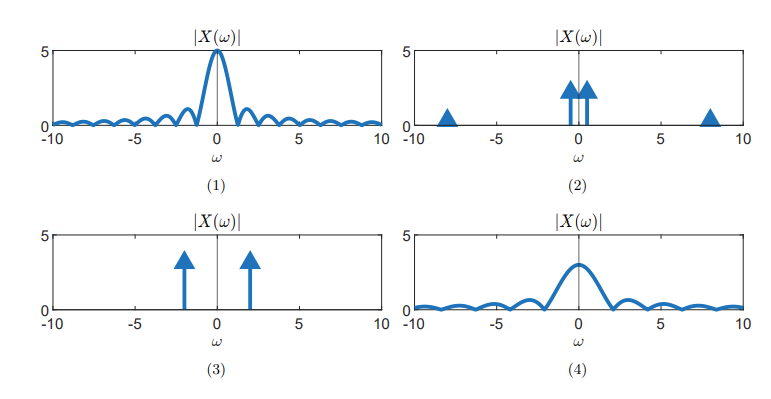
Signals in the frequency domain.

Solution:
Periodic signals are always characterized by Dirac pulses in the Fourier domain. signals and have only sinusoidal components and therefore fall into this category. The main contribution of signal is slower than signal , but signal also has an extra high frequency component. Therefore:

Signals and are rectangular pulses and are therefore aperiodic. The shorter pulse is more stretched in the Fourier domain and vice versa. This is known as the time scaling property:

Therefore, stretching the signal in the time domain will cause the signal to contract in the Fourier domain.
What about a shift in time as is the case signal ? If , then by the time shift property:

Therefore, the shift in time only influences the phase of the signal and therefore has no effect on the magnitude of the spectrum , which is what we plot in figure .

Question 3

Consider the signal :

where

shown in the following figure:

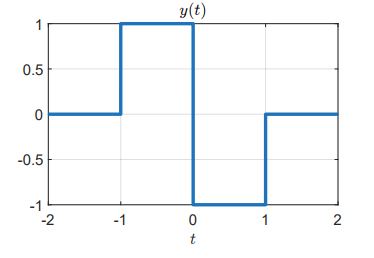
The signal

Part a

Show that .

Solution:
We know that:

Differentiating each section of this function yields:

Therefore:

Part b

Find the Fourier transform of .

Solution:
By definition:

To get the result in the official answer, we can:

Therefore:

Part c

Find the Fourier transform of the following signal by the using the previous result:

Solution:
By the scaling property:

Question 4

Consider .

Part a

Find the Fourier transform of this signal.

Solution:
First, we’ll show that by definition:

By Euler’s formula:

Cool. Now we can use the time scaling property (and also linearity) to say:

Therefore, by the duality property:

where the fact that was used.

Part b

Use Parseval’s theorem

where and and , to calculate the -norm squared of .

Solution:
It is not trivial at all to calculate the integral of the . Luckily, we can use the given Parseval’s theorem:

Which is why:

Question 5

Consider the signal defined as

Part a

Our signal contains a “slow” and a “fast” part. Identify them.

Solution:
In terms of frequency, is slower because .

Part b

Identify the period and the fundamental frequency .

Solution:
The period is the least common multiple of the periods of both parts. In our case it’s simple because is a multiple of :

Therefore:

Part c

Decompose this signal into its Fourier series.

Solution:
There are two approaches to solving this problem:

1. By definition:
2. Party tricks:
   By Euler’s formula we know that: Therefore, we can write in a different way: We have identified all of the Fourier coefficients:

Part d

Apply the Fourier transform to this signal.

Solution:
Using the result from the previous part, by the delta function property:

Therefore:

Question 6

Consider the signal defined as

Part a

Identify the period and the fundamental frequency .

Solution:
The function repeats every units of time, therefore:

Part b

Decompose this signal into its Fourier series.

Solution:
By definition:

To solve the integral, we notice by Euler’s formula that:

Which is why:

Substituting back to :

I don’t know where the second term is supposed to disappear, but in the official answer:

Part c

Derive the time shift property of Fourier series: If , then .

Solution:
If , then:

substituting , which means , we get:

Therefore:

Part d

Use the previous results and the time shift property to derive the Fourier series of the signal in the previous part, i.e. .

Solution:
The time shift is equal to . Therefore, using the previous answers, we get:

Question 7

Let be the -periodic signal such that:

Determine the Fourier coefficients and write down the Fourier series of .

Solution:
The function repeats every units of time, so that:

By definition:

Notice that specifically for :

Therefore:

← Previous: LSY1_007Next: LSY1_009 →