LSY1_002 Signals and Convolutions

← Previous: LSY1_001Next: LSY1_003 →

Standard signals

The following definition introduces basic signals that play a prominent role in this course:

• step:

  𝟙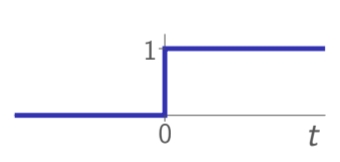

  

• ramp:

  𝟙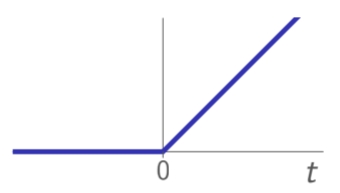

  

• rectangular pulse (of width ):

  

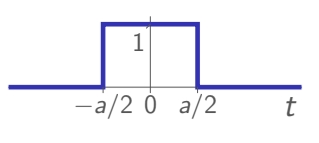
• triangular pulse (of width ):

  

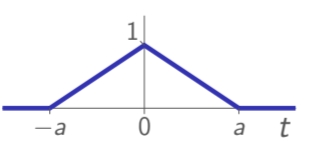
• sinusodial:

  

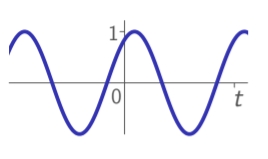
• sinc (sine cardinal):

  

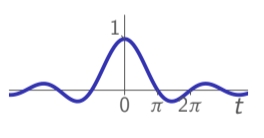
• exponential:

  

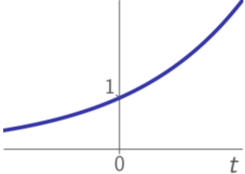
Notes:

Common abbreviations are:

Norms

We can define signal norms in a very similar way to vector norms:

Definition:

• -norm: If , then we say that and call absolutely integrable.
  • -norm:
  If , then we say that and call square integrable.
  • -norm:
  If , then we say that and call it bounded

Example: Standard signals' norms

• if , then
  • if 𝟙 with , then
  • if 𝟙 then

Operations on Signals

(Amplitude) Scaling

Given and , the signal (or ) is defined as

with .

Example:

𝟙

Addition

Given and , the signal is defined as

Multiplication

Given and , the signal (or ) is defined as

Time Scale (pace change)

Given and , the signal is defined as

Commutativity property:

Time Shift

Given and , the signal is defined as

Commutativity property:

Periodic Signals

A signal is periodic if a exists such that for all . A signal will be referred to as -periodic if it is periodic with period .

Defintion:

A real-valued signal that can be written as

is called a sinusoid or real harmonic signal. Then is the amplitude, the angular frequency, and the initial phase of the signal .

Such sinusoids have a period of .

Lemma:

Suppose that is integrable on and that is periodic with period . Then for every , there holds:

Energy and Power

It is customary in signal analysis to use “energy” instead of norm:

Definition:

The energy of a signal is defined as

If (finite energy content), then the signal is said to be an energy signal.

The rectangular and traingular pulses are examples of energy signals. For a signal to have a finitie energy content it is necessary that converges. Consequently, signals like sinusoids, periodic signals and the unit step and many others, are not energy signals. In such cases it is customary to consider instead its averages energy per unit time, i.e., to look at its (averaged) power.

Definition:

The power of a signal is defined as

Signals that have finite power are called power signals.

Example:

In the case of a -periodic signal, the power signal is finite, and it equals the average energy over one period:

Let there be such that :

Example:

The power of the sinusoid with period , is:

Convolution

Loosely speaking a convolution is a linear combination of shifted copies of signal. For instance:

Is an example of convolution of signal . Note that the convolution is itself a signal. More generally expression like:

are known as convolutions, and so is its integral version which we take to be its definition.

Definition:

The convolution or convolution product of two signals and is denoted as and is defined as:

It is an interesting fact that convolution products commute:

Convolutions are very common in applications, and are, for instance, useful if we want to remove noise from signals, detect edges in pictures, soften pictures, etc.

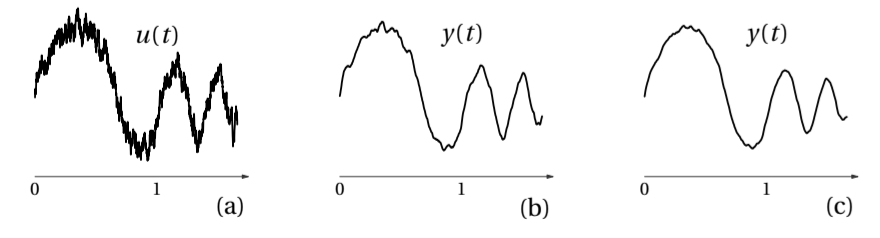
Example: Sliding window averaging and noise reduction

For a given signal we construct the signal by averaging around over an interval of a fixed length , i.e., we consider

Averaging this way filters out highly fluctuating noise. It is to be expected then, that is somewhat smoother that , but as long as is not too large the graph of the averagd should retain roughly the same shape as the graph of .

Screenshot_20240609_111610_Samsung Notesveraged with

The signal can be written as the convolution of with a suitable function :

for

Screenshot_20240609_112515_Samsung Notes 1

Example: Convolution with step:

Convolution with the unit step amount to integration:

𝟙𝟙𝟙𝟙

For the step signal, we get zero for every , therefore the second integral evaluates to :

𝟙

The Delta Function

In applications we often encounter signals that a very short duration but nevertheless have a definite impact. Such signals are called impulses. The standard are called impulses. The standard impulse is the so-called Dirac delta function also known as the unit impulse. The delta function is introduced as the limit as of

As goes to infinity, the rectangular pulses become spikier and spikier, with spike around .

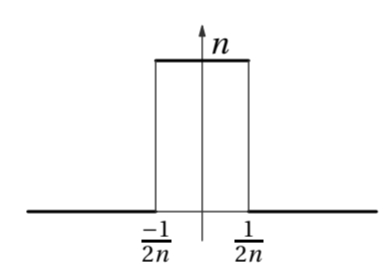
A series of for and

However, the area enclosed by the spike and the -axis, , equals independent of . We now naively define delta function as the limit

and we think of the delta function as a “function” that is zero everywhere except at where it has a spike so large that

The delta function is usually depicted as

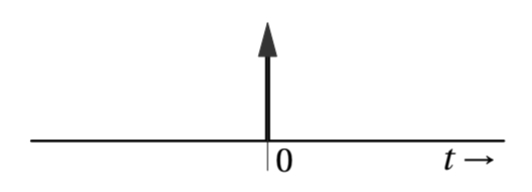
The delta function

The idea to see the function as a pike in this sense is helpful, but mathematically it is far from sound. After all,

and the integral of a function that is zero everywhere except for one point, is zero.

Lemma:

If is continuous at , then

Properties of the delta function

Delta functions can be added, they can be multiplied with regular functions, they can be integrated etc.

The Sifting Property

The scaled and shifted delta function we take to be defined as:

For the argument is zero, so as a function of is centered around .

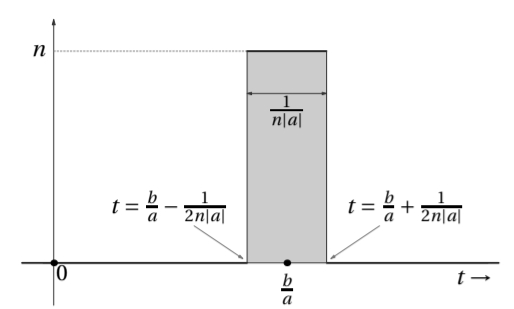
Shifted and scaled

This is very much like a shifted copy of with the difference that the spike does not have a unit area:

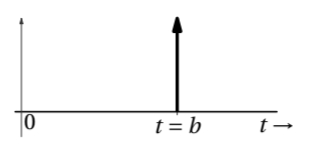
Shifted delta function

We can now generalize the previous Lemma:

Lemma:

If is continuous, then:

An immediate special case is that

This property is known as the sifting property of the delta function. It is the property that out of all values that can take, the value at is sifted out. It is also possible to determine the convolution product of a signal and the delta function .

Products with delta functions

Lemma:

If is continuous at , then

Property	Condition	Notes
Sifting		continuous at
		continuous
Convolution
Scaling
	𝟙

Properties and rules of calculus for the delta function

Exercises

Question 1

Consider the continuous time signal

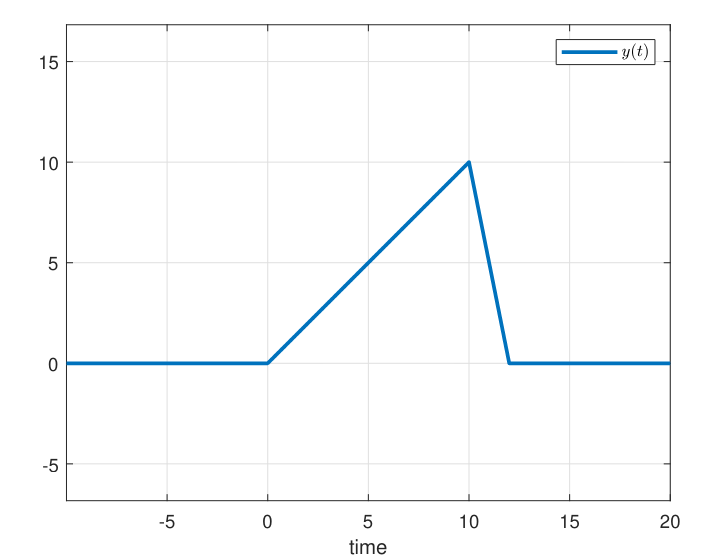
Triangle signal

Construct using the step function 𝟙, and the signal. Compute the and norms of .

Solution:

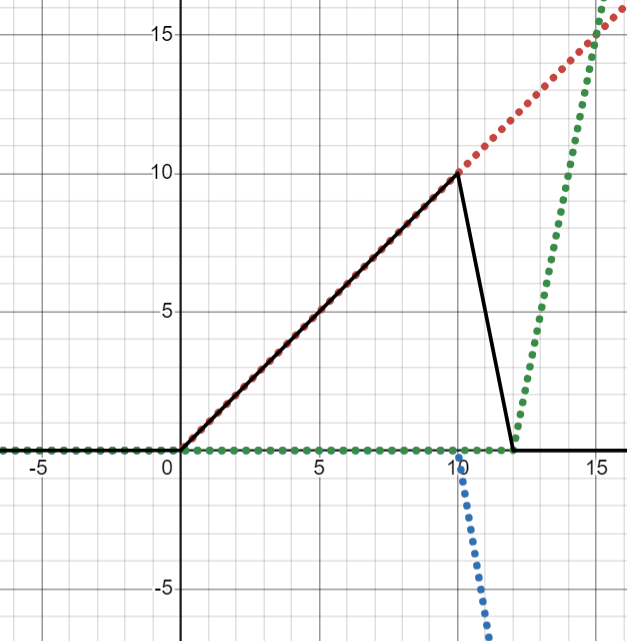
The above mentioned signal, broken down to three signals. Try to match the signals to their corresponding graph representation.

According to signal norm:

We have:

Question 2

Let be the signal from Question 1. Let , where:

i.e.

find the convolution .

Solution:
One of the properties of Convolution is:

We’ll calculate each one individually, using the The Sifting Property:

and we end up with

← Previous: LSY1_001Next: LSY1_003 →