נגדים חשמליים

האם הקיום של זרם חשמלי מעיד על מפל מתחים?

לא בהכרח. מחוק פאראדיי, כאשר יש לנו סליל מוליך שעובר בניצב למישורו שדה מגנטי משתנה, מתפתח כא”מ בסליל ולפיכך זרם דרכו. במקרה זה, הזרם נוצר ללא מפל מתחים חיצוני - הכא”מ המושרה הוא זה שמניע את הזרם. כמו כן, במוליך-על אידיאלי, זרם יכול לזרום ללא מפל מתחים כלל בגלל ההתנגדות האפסית.

נגד לינארי מקיים את חוק אוהם:

כאשר היחידות של ההתנגדות הן:

האנרגיה הנפלטת מהנגד (לרוב כחום) היא:

והיא בעלת יחידות של הספק:

בניית נגד מתבססת על כך שההתנגדות פרופורציונלית לאורך הנגד ופרופורציונאלית הפוכה לשטח החתך שלו:

כאשר היא ההתנגדות הסגולית (specific electrical resistance) של החומר, עם יחידות:

נגדים במיקרו-מערכות

במיקרו-מערכות אנו מייצרים נגדים ע”י תבנית של שכבה מוליכה, לרוב בצורת נחש (meander):

איור 11.1: תבנית נחש (meander) של נגד במיקרו-מערכת.

בהנחה שלחומר המוליך יש עובי ורוחב , ההתנגדות של הנחש היא:

כאשר ל- יש יחידות של וליחס יש יחידות של ריבועים (squares). מבחינת ייצור, נוכל להוסיף עוד מהמוליך (להאריך את הנחש) עד שמתקבלת ההתנגדות הרצויה.

מדידת התנגדות שכבות - ארבע נקודות מגע

התנגדות שכבות דקות לרוב נמדדת ע”י מדידת ארבע נקודות מגע (four-probe measurement), הנקראת גם four-terminal sensing.

איור 11.2: סכמה של מדידת ארבע נקודות מגע.

בשיטה זו, אנו שולטים בזרם ומודדים את המתח באזור שבו הזרם אחיד על פני הפלטה. בצורה זו נמנעים מרגישות להתנגדות המגע (contact resistance). ברגע שיש לנו את התנגדות שכבה הרצויה, אנו מעצבים בהתאם.

משוואת החום

משוואת ההולכה

בנגד תרמי חד-ממדי לינארי, הקשר בין שטף החום לטמפרטורה נתון ע”י משוואת ההולכה:

כאשר שטף החום בעל יחידות:

ומקדם ההולכה התרמית הוא:

הדיברגנץ של שטף החום הוא כמות החום המצטברת בחומר. הצטברות חום זו מגדילה את הטמפרטורה לפי:

כאשר הוא הצפיפות הנמדדת ב-, ו- הוא קיבול החום הסגולי (heat capacity) הנמדד ב-.

אם מספקים עוד חום למערכת, המשוואה השולטת היא:

כאשר הוא החום המסופק למערכת ביחידות של .

משוואת החום החסרת ממדים

נביט במשוואת החום הלינארית:

נרמול המרחב

ננרמל את המרחב ע”י האורך האופייני :

נציב לקבלת:

הדיפוסיביות התרמית

נגדיר את הדיפוסיביות התרמית:

עם יחידות:

נציב לקבלת:

נרמול הטמפרטורה

ננרמל את הטמפרטורה ביחס לטמפרטורת הסביבה :

נציב לקבלת:

הערות:

לאיבר אין יחידות:

לאיבר יש יחידות של זמן, והוא מייצג את הזמן האופייני של הבעיה:

נרמול הזמן

ננרמל את הזמן לפי הזמן האופייני:

נקבל את משוואת החום החסרת ממדים:

הטבלה הבאה מציגה את הפרמטרים התרמיים והחשמליים של חומרים נפוצים במיקרו-מערכות:

סמל	משתנה	יחידות	סיליקון	אלומיניום
	צפיפות
	קיבול חום
	הולכה תרמית
	התנגדות סגולית
	דיפוסיביות תרמית

הערה:

* ההתנגדות הסגולית של סיליקון תלויה מאוד ברמת הסימום (doping level).

שפעול תרמואלסטי

עקרון הפעולה

בשפעול תרמואלסטי (thermoelastic actuation) משתמשים בעיבורים הקטנים הנגרמים עקב עלייה בטמפרטורה כדי להשיג תזוזות גדולות.

עקרון הפעולה:

חימום: שימוש בחימום ג’אולי (Joule heating) להעלאת הטמפרטורה
קירור: שימוש בהולכה והסעה להורדת הטמפרטורה

הערות:

יתרונות:

מבנים וחומרים פשוטים

תאימות לטכנולוגיות ייצור מיקרו

מתחי IC יכולים לייצר מיליוואטים של חום

חסרונות:

צריכת הספק גבוהה

תגובה איטית יחסית

סוגי משפעלים תרמואלסטיים

קיימים שלושה סוגים עיקריים של משפעלים תרמואלסטיים:

זרועות חמות/קרות (Hot/Cold Arms)

משפעל המבוסס על שתי זרועות מקבילות עם שטחי חתך שונים. כאשר זרם זהה עובר דרך שתי הזרועות, הזרוע הדקה (עם התנגדות גבוהה יותר) מתחממת יותר ומתפשטת יותר, מה שגורם לכיפוף של המבנה.

TODO: להוסיף

משפעל זרועות חמות/קרות.

משפעל בימורפי (Bimorph Actuator)

משפעל המורכב משני חומרים עם מקדמי התפשטות תרמית שונים. כאשר הטמפרטורה משתנה, כל שכבה מתפשטת בשיעור שונה, מה שגורם לכיפוף של המבנה.

משפעל בימורפי.

משפעל קפיצה תרמית (Thermal Buckling Actuator)

משפעל המבוסס על קורה דחוסה הנמצאת קרוב לנקודת אי-יציבות. חימום קטן גורם להתפשטות שמעבירה את הקורה מעבר לנקודת הקפיצה, מה שמייצר תזוזה גדולה.

משפעל קפיצה תרמית.

דעיכה תרמואלסטית

מקדם זנר

לפי זנר (Zener)¹, הדעיכה התרמואלסטית (thermoelastic damping) בתנודות של קורות פרופורציונלית ל:

כאשר הוא פקטור האיכות, הוא התדירות הזוויתית, ו- הוא קנה המידה הזמני התרמי האופייני.

מקדם זנר (Zener coefficient) מוגדר כ:

כאשר הוא מקדם ההתפשטות התרמית, הוא מודול יאנג, הוא הצפיפות, ו- הוא קיבול החום הסגולי.

הערה:

ניתן לאמת שלמקדם זנר יש יחידות של:

תרגילים

תרגיל 1

התרגיל יציג ניתוח כללי של מעבר חום בקורה, סקירה קצרה על משפעל שברון ועל דרכי ייעול מתוך המאמר שפורסם ב-JMEMS¹, וסרטון מבוסס על המאמר:

בעיית מעבר חום

נתונה קורה רתומה-רתומה הנמצאת תחת חימום ג’אולי. נתונה קורה באורך ושטח חתך .

קורה רתומה-רתומה תחת חימום ג’אולי.

נדרש לחשב את פילוג הטמפרטורה בקורה, בהנחה שההסעה זניחה ושטמפרטורת העוגנים וקבועי החומר נשארים קבועים בקירוב.

פתרון:
משוואת מעבר החום, כאשר המנגנון השולט הוא הולכה:

כאשר הספק החום הסגולי, אנחנו מדברים על חימום ג’אולי (נוצר מזרם חשמלי) לכן:

כאשר:

- הוא ההספק החום (שימו לב כי בהרצאות לפעמים אות זו מייצגת הספק חום סגולי)
- שטח החתך של הנגד (במקרה שלנו זה חתך הקורה)
- אורך הנגד (אורך הקורה)
- היא ההתנגדות החשמלית של הנגד (הקורה)

ההתנגדות החשמלית נתונה על ידי:

כאשר הינה ההתנגדות הסגולית של החומר.

הערה:

באופן עקרוני משתנה עם הטמפרטורה בקשר מהצורה , אבל בתרגיל זה (ובהרבה מקרים הנדסיים שימושיים) אנחנו נתייחס לערך כקבוע ושווה לערכו בטמפרטורה .

לכן מתוך חוק אוהם נקבל:

נציב למשוואת ההולכה:

קיבלנו מד”ר מסדר שני במשתנה . כדי לפתור את המשוואה דרושים לנו שני תנאי שפה. נניח כי בריתומים הטמפרטורה לא משתנה (אזורי הריתום גדולים):

זו משוואה פרידה לכן קל לבצע נגזר אינטגרציה פעמיים למציאת פילוג הטמפרטורה:

נציב תנאי שפה:

את פילוג הטמפרטורה נוכל לרשום:

נציב את תנאי השפה השני:

הפתרון שקיבלנו עבור פילוג הטמפרטורה:

נראה שקיבלנו פילוג טמפרטורה פרבולי. כאשר המקסימום מתקבל במרכז כלומר ב- (אם לא רואים זאת ישר, אפשר להסתכל על הנגזרת הראשונה ולהשיק או לחשוב במונחים של סימטריה).

הטמפרטורה המקסימלית:

תרגיל 2

נסתכל על שתי הקורות הבאות - כאשר אחת ארוכה מהשנייה פי . באיזה מהקורות הטמפרטורה תהיה גבוהה יותר אם נתון שמופעל על שתי הקורות אותו מתח?

איור 11.3: שתי קורות באורכים שונים.

פתרון:
הטמפרטורה המקסימלית בשתי הקורות תהיה זהה.
ראשית ניתן לראות זאת מהביטוי עבור הטמפרטורה המקסימלית:

כל הפרמטרים נשארים אותו דבר פרט לאורך שגדל פי וההתנגדות שתלויה ליניארית באורך. כלומר:

כאשר אנחנו מפעילים את אותו מתח, הטמפרטורה המקסימלית תהיה זהה לכל קורה, ללא תלות באורכה.

איור 11.4: התפלגות טמפרטורות זהה בשתי הקורות.

תרגיל 3

מה קורה אם אנחנו מאריכים את הקורה על ידי קיפולה ל-?

איור 11.5: קורה ישרה לעומת קורה מקופלת.

פתרון:
גם במקרה הזה הטמפרטורה המקסימלית בשתי הקורות תהיה זהה.

הבעיה עדיין חד ממדית. אפשר לדמיין שפשוט “קיפלנו” את הפרבולה. עדיין הגדלנו את ההתנגדות פי שתיים והורדנו את השטף (שיפוע הפרבולה) בחצי. גם כאן אינו תלוי באורך.

איור 11.6: פרבולות הטמפרטורה לשני המקרים.

תרגיל 4

המאמר ¹ מציג שתי דרכי ייעול של משפעל סטנדרטי, שנבנה כחלק מתחרות “משיכת חבל” של משפעלים בין סטודנטים מאוניברסיטת הונג קונג ואוניברסיטת קיוטו.

המאמר עוסק במשפעל מסוג שברון. כדי להבין את עיקרון הפעולה, נדמיין קורה רתומה-רתומה, תחת חימום ג’אולי. אם לא מאפשרים לקורה להתפשט בכיוון הארוך, מאמצים נבנים, והקורה עלולה לקרוס לכיוון מסוים.

הקורות כולן מחוברות במרכזן ל-shuttle שאותו רוצים להזיז. כל הקורות רוצות להתארך ובכך גורמות לתזוזת ה-shuttle. השימוש במספר קורות הוא על מנת לייצר יותר כוח.

איור 11.7: משפעל שברון - מבנה כללי.

בעיה ראשונה עליה רוצים להתגבר:
ה-shuttle עצמו מתארך כתוצאה מהתפשטות תרמית. מה שאומר שבעצם הקורות העליונות תורמות פחות לתזוזה מהתחתונות.

פתרון מהמאמר: שימוש בקורות באורך וזוויות משתנים.

התכן הוא הגדלה הדרגתית של האורך ושל הזוויות של קבוצות של כ-10 קורות כל פעם. כך הקורות הכי קרובות לקצה מתארכות הכי הרבה ומהוות פיצוי להתארכות ה-shuttle.

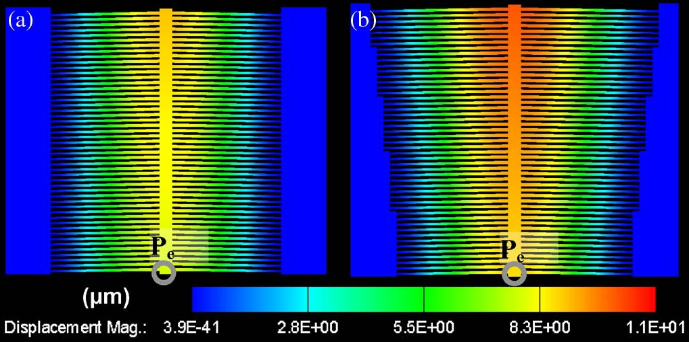
bscreen

איור 11.8: פתרון לבעיה הראשונה - קורות באורך וזוויות משתנים.

בעיה שניה עליה רוצים להתגבר:
הטמפרטורה המקסימלית מרוכזת באזור מאוד צר כלומר רק חלק קטן מהקורה מרגיש אותה. לכן רק אזור קטן תורם להתארכות.

פתרון מהמאמר: שינוי שטח החתך.

על ידי שינוי שטח החתך אנחנו “מורחים” את הפרבולה ויותר מהקורה נמצאת בטמפרטורה גבוהה יותר שגורר ההתארכות יותר גדולה.

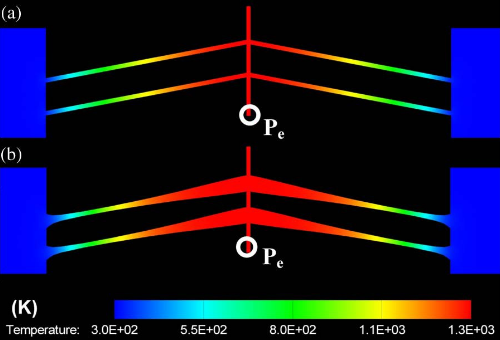
bscreen

איור 11.9: פתרון לבעיה השנייה - שינוי שטח החתך.

“Improved Designs for an Electrothermal In-Plane Microactuator”, Alex Man Ho Kwan et al. ↩ ↩²

Zener, C., 1937. Internal friction in solids. I. Theory of internal friction in reeds. Phys. Rev. 52, 230–235. ↩

פנגייה

MCS1_011 תרמואלסטיות

נגדים חשמליים

נגדים במיקרו-מערכות

מדידת התנגדות שכבות - ארבע נקודות מגע

משוואת החום

משוואת ההולכה