MDN1_006 תמסורות מכאניות

→ קודם: MDN1_005הבא: MDN1_007 ←

מבוא

בפרק זה נעסוק בגאומטריית תמסורות (גג”שים), הקשרים הקינמטיים ביניהם, והכוחות המועברים ביניהם ע”י ארבעה סוגי תמסורות שונים: חלזונית, ישרה, משופעת, קונית. הכוחות המועברים בין תמסורות משולבות מעבירות מומנטי פיתול לגלים לתנועה ותמסורת הספק, ויוצרים כוחות ומומנטים המשפיעים על הגלים והמסבים שלו.

סוגי תמסורות

לתמסורת ישרה (spur gear) יש שיניים מקבילות לציר הסיבוב והן מוסרות תנועה מגל אחד לגל אחר המקביל לו. מכל הסוגים השונים של תמסורות, הוא הכי פשוט, וניעזר בו כדי לפתח את הקשרים הקינמטיים.

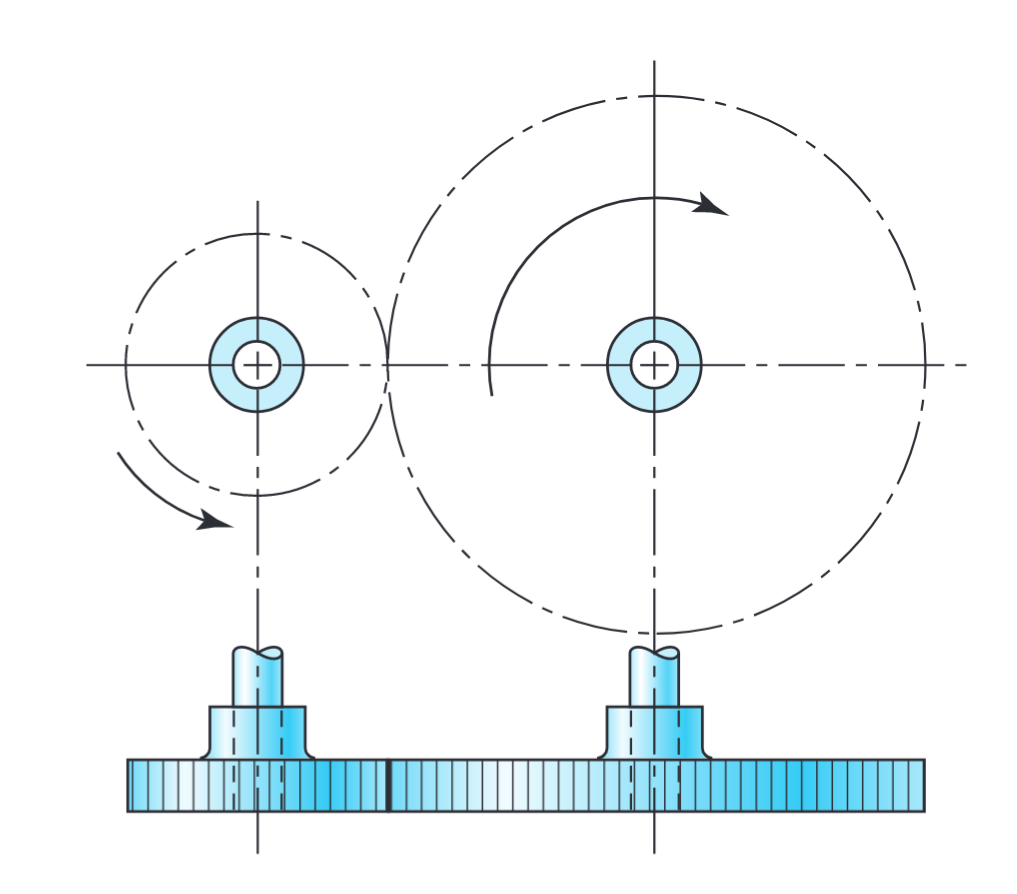
תמסורת ישרה מעבירה תנועה סיבובית בין גלים מקבילים. (Budynas et al., 2015).

לתמסורת משופעת (helical gears) יש שניים בזווית לציר הסיבוב. מטרתה זהה לזו של תמסורת ישרה, והן פחות רועשות בגלל מגע יותר מתון בין השיניים. השיניים המשופעות גם מפתחות עומסים לאורכם ומומנטי כפיפה, שלא קיימים בתמסורת ישרה. לפעמים משתמשים בתמסורות משופעות לתמסורת תנועה בין גלים לא מקבילים.

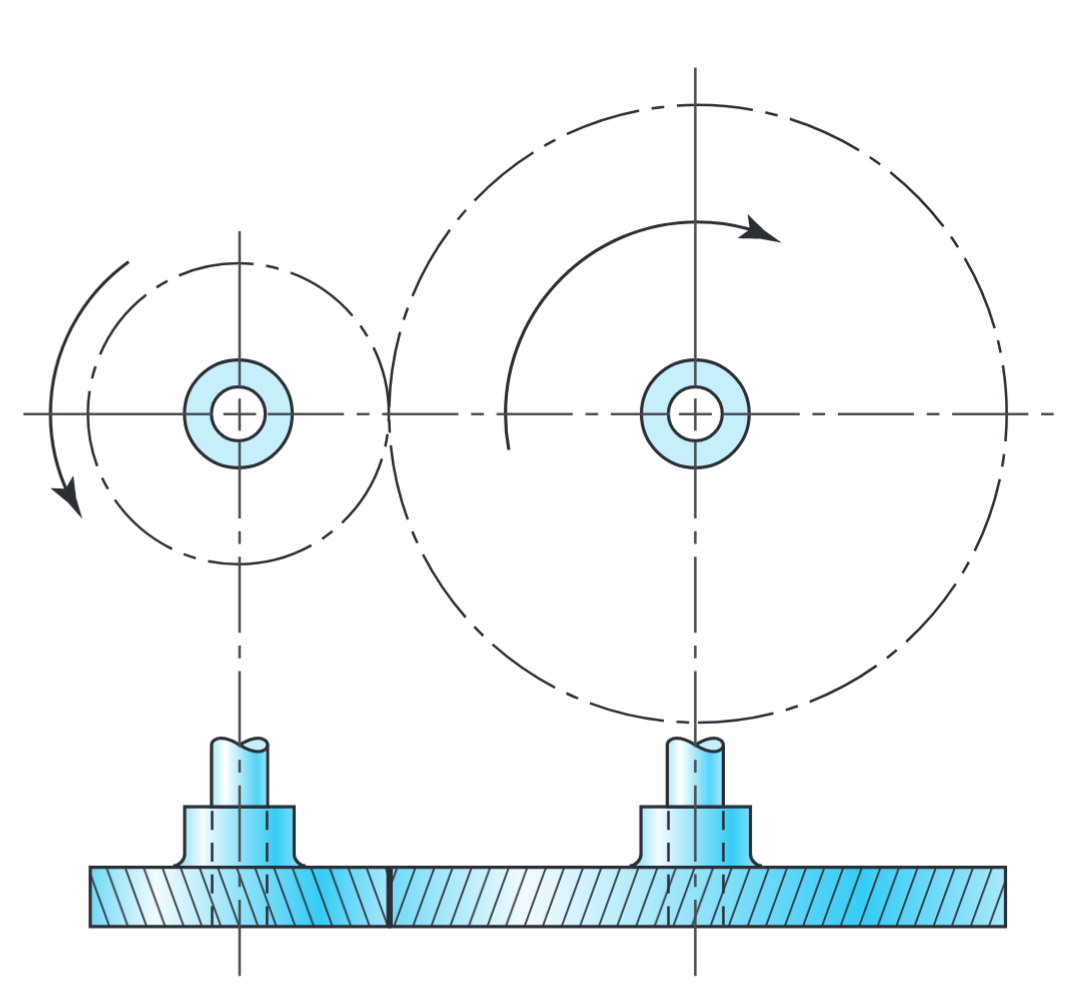
תמסורת משופעת להעברת תנועה בין גלים מקבילים (וגם לא מקבילים). (Budynas et al., 2015).

לתמסורות קוניות (bevel gears) יש שיניים שיוצרו על מישורים קוניים, ולרוב משומשים בתמסורת תנועה בין גלים החותכים אחד את השני. האיור הבא מתאר תמסורת קונית בשן ישרה, לעומת תמסורת קונית ספירלית הנחתכת כך שהשן כבר לא ישרה, אלא יוצרת קשת מעגלית.

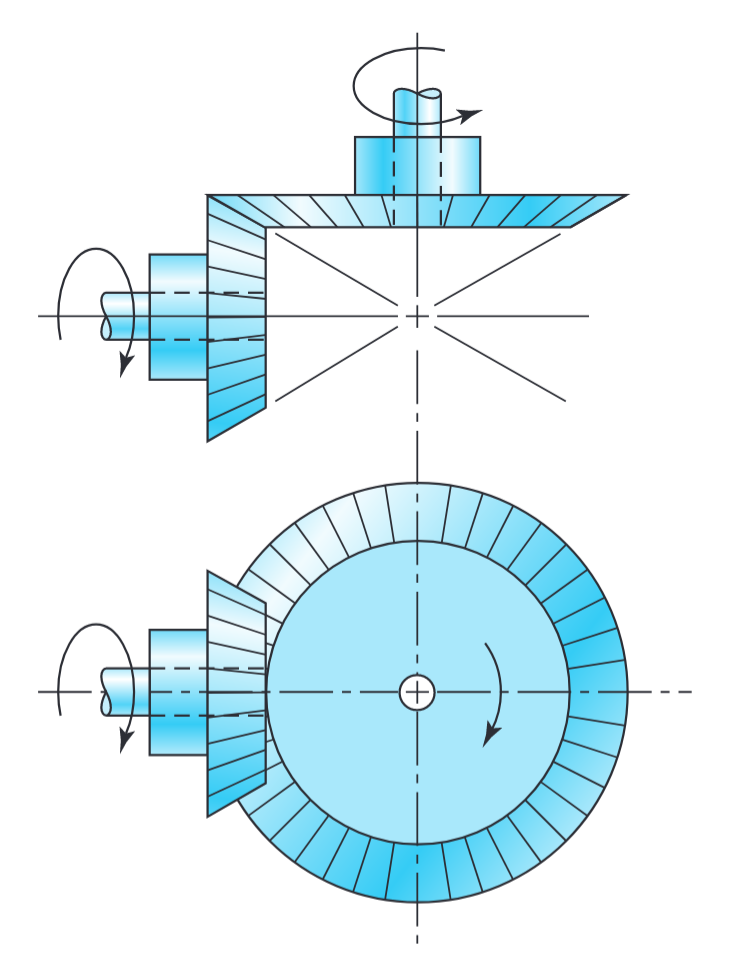
תמסורות קוניות מעבירות תנועה סיבובית בין גלים נחתכים. (Budynas et al., 2015).

תמסורות חלזוניות (worm gears), כפי שמוצג באיור הבא, הן למעשה בורג. הכיוון של סיבוב הבורג החלזוני תלוי באם הוא נחתך לפי כלל יד ימין או שמאל. התמסורת החלזונית גם מיוצרת כך שהשן של אחת מהגג”שים, או שניהם, משולבת עם השנייה.

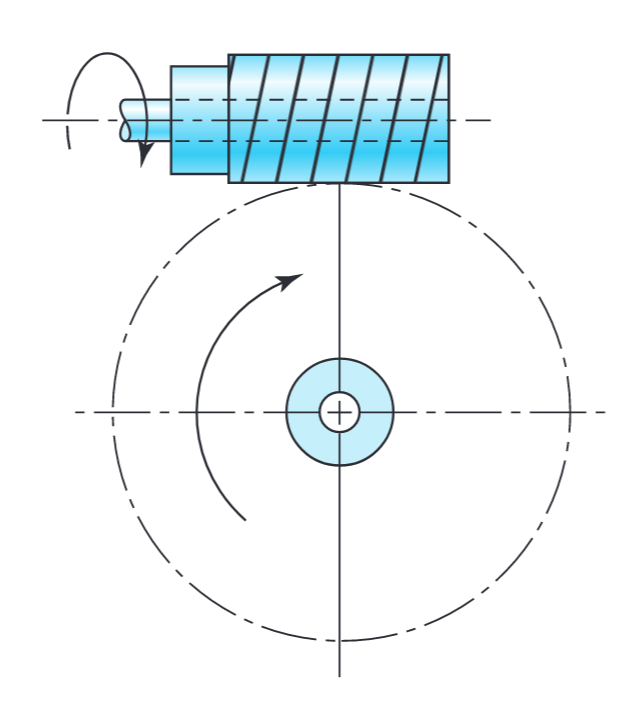
השימוש של תמסורת חלזונית להעברת תנועה סיבובית בין גלים שלא מקבילים או חותכים אחד את השני. (Budynas et al., 2015).

מערכת גג”ש

באיור הבא מוצגת מערכת גג”ש (gear train), נניח שגג”ש מניע את גג”ש :

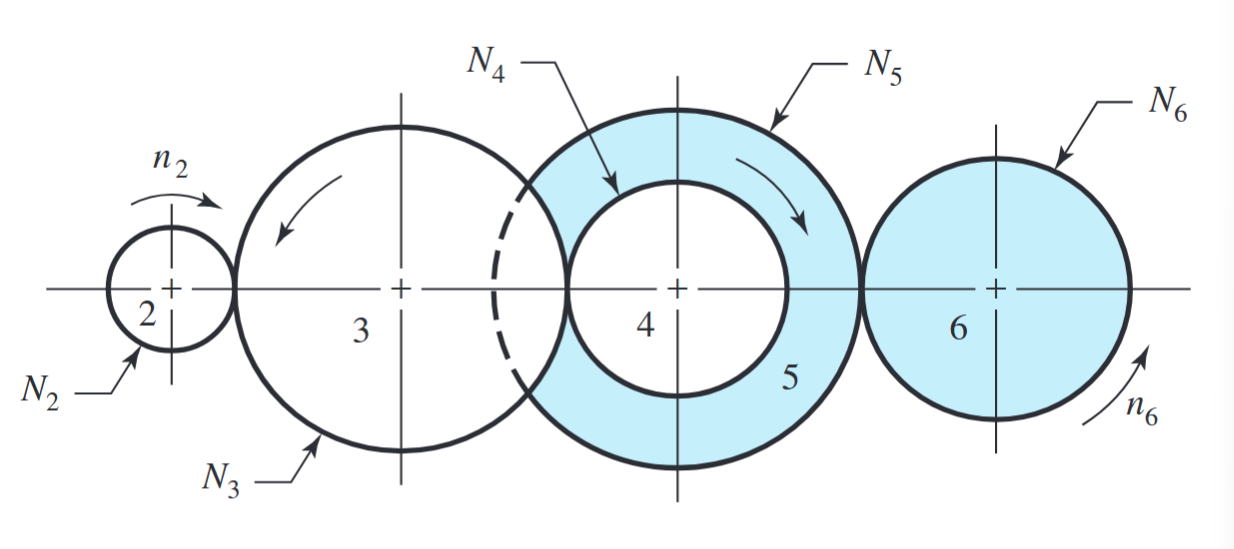
מערכת גג”ש. (Budynas et al., 2015).

המהירות של הגג”ש המונע היא:

כאשר הוא מספר הסיבובים לדקה - ; הוא מספר השיניים; ו- הוא קוטר הפסיעה.
משוואה זו תקפה לכל סוג תמסורת. הערך המוחלט מעיד על כך שאין תלוי באם כיוון הסיבוב הוא חיובי או שלילי. במקרה של תמסורות ישרות ומשופעות, סימן הכיוונים לרוב מוחלט לפי כלל יד ימין - חיובי נגד כיוון השעון, ושלילי עם כיוון השעון. כאשר מדובר בתמסורות קוניות או חלזוניות, כיווני הסיבוב טיפה יותר קשים לקביעה, אבל לא ניכנס לזה בקורס.
במערכת גג”ש המוצגת לעיל ישנם 5 גג”שים. בהנחה וגג”ש הוא הגג”ש המניע, מהירות הסיבוב של גג”ש היא:

עבור זוג גג”שים בו אחד מניע את השני, אנו קוראים לגג”ש המניע פיניון (pinion), ולגג”ש המונע גיר (gear).

הערה:

בקורס נתייחס לתמסורות מפחיתות ולכן הגג”ש המניע הינו הגג”ש הקטן - ה-pinion.

נשים לב שגג”ש הוא בטלן (idler). להמחשת תפקידו, נשרטט את המערכת מלמעלה:

מבט על הגג”ש.

הצורה היחידה שבה הבטלן משפיע על גג”ש הוא בכיוון הסיבוב של , ולא במהירות הסיבוב שלו, ולכן הוא נקרא בטלן. המשוואה לעיל תהפוך ל:

במערכת שלנו, גג”שים ו- הם המניעים, בעוד הם המונעים.
נגדיר את המקדם של כמקדם הנקרא train value, שהוא בעצם ההופכי ליחס התמסורת . הוא מוגדר באופן הבא:

כעת נוכל לרשום:

כאשר הוא מהירות הגג”ש הראשון במערכת ו- הוא האחרון.
כלל אצבע כללי הוא לבחור train value עד עבור זוג גג”שים ישרים. אם מדובר בתמסורת משופעת, אפשר יחס של עד . יחסים יותר גבוהים דורשים כבר יותר גג”שים, ואפשר לחבר אותם באופן שיתפוס פחות מקום ע”י חיבורם בשלב נוסף. מערכת גג”ש דו-שלבית, כפי שמוצג באיור הבא, יכולה להגיע ל-train value עד :

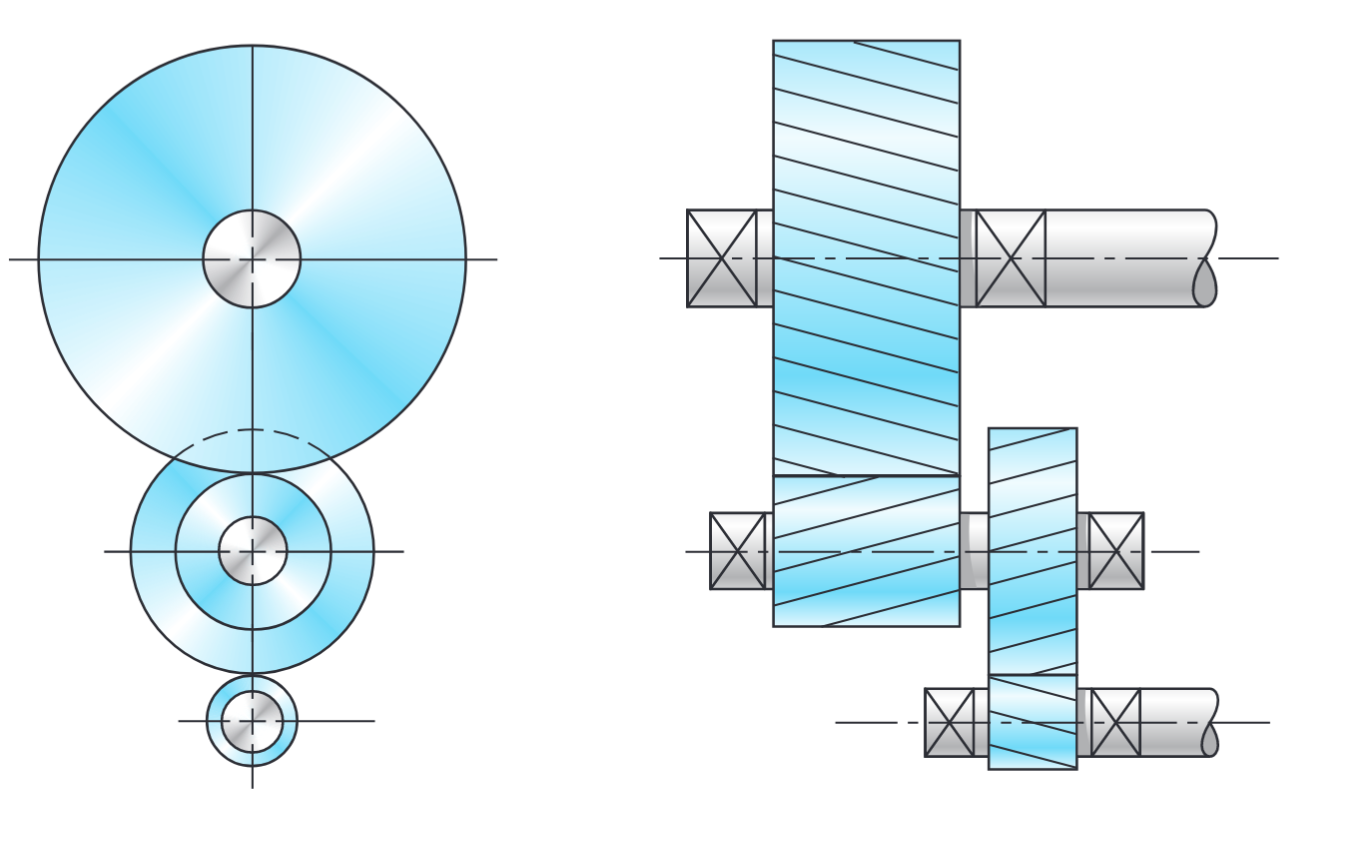
מערכת גג”ש דו-שלבית. (Budynas et al., 2015).

לפעמים גם נרצה שהגל כניסה וגל יציאה יחוברו באותו הקו, כפי שמוצג באיור הבא, לקבלת מערכת גג”ש בתשלובת הפוכה (compound reverted gear train):

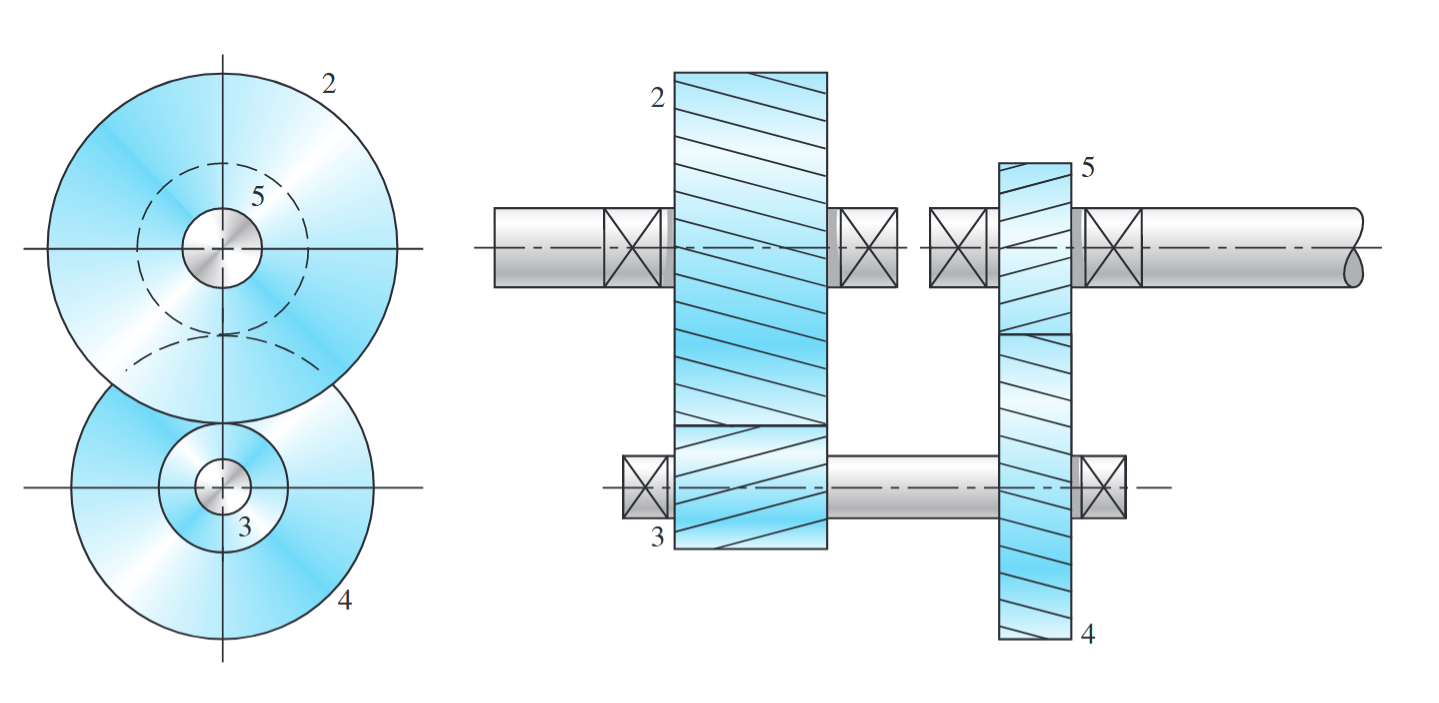
מערכת גג”ש בתשלובת הפוכה. (Budynas et al., 2015).

מערכת זו דורשת שהמרחקים בין הגלים יהיו זהים עבור שני שלבי המערכת, שמוסיף על מורכבות התכן. אילוץ זה הוא:

נוכל לתרגם את תנאי זה לתנאי על מספר השיניים - אם המודול זהה בין הגג”שים:

תמסורת פלנטרית

אם מאפשרים לחלק מצירי הגג”שים להסתובב סביב צירים אחרים, מקבלים מערכת גג”ש הנקראת תמסורת פלנטרית. תמסורות פלנטריות כוללות גג”ש שמש (sun gear), זרוע פלנטרית (planet carrier), ואחד או יותר גג”ש לווין (planet gear).

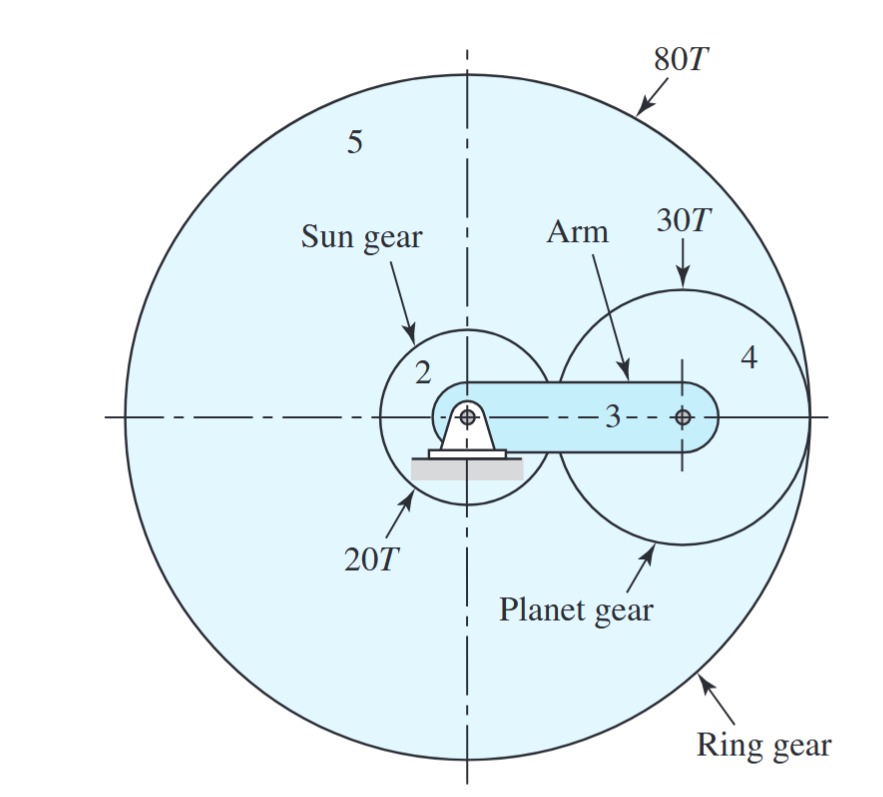
מערכת גג”ש פלנטרית. (Budynas et al., 2015).

תמסורות פלנטריות הן מכניזמים יוצאי דופן כי יש להם שתי דרגות חופש; כלומר, לתנועה מאולצת, המערכת צריכה לקבל שני קלטים. באיור לעיל שני הקלטים האלו יכולים להיות התנועה של שתי אלמנטים כלשהם במערכת. נוכל להגדיר למשל שגג”ש השמש יסתובב ב- עם כיוון השעון, והגג”ש טבעת יסתובב ב- נגד כיוון השעון. עם שני קלטים אלו, נקבל את תנועת הזרוע.

האיור הבא מראה תמסורת פלנטרית המורכבת מגג”ש שמש , זרוע , ולוויינים ו-.

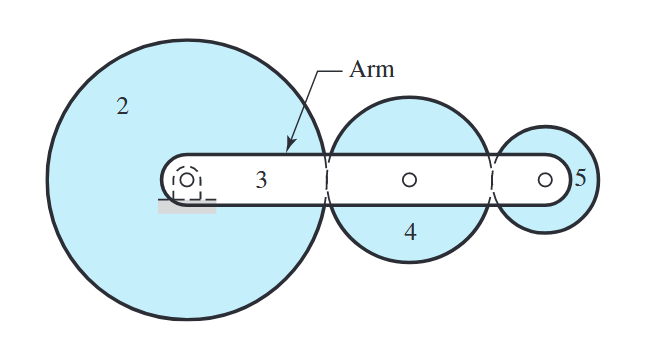
מערכת גג”ש על הזרוע של תמסורת פלנטרית. (Budynas et al., 2015).

המהירות הזוויתית של גג”ש יחסית לזרוע ב- היא:

בנוסף, המהירות הזוויתית של יחסית לזרוע היא:

אם נחלק את שתי המשוואות נקבל:

משוואה זו מתארת את היחס בין גג”ש לגג”ש , ושתי המהירויות נלקחות ביחס לזרוע. יחס זה הוא גם זהה ליחס השיניים בין הגג”שים, בין אם הזרוע מסתובבת, או לא - זהו ה- train value. לכן נוכל לרשום:

נוכל להיעזר בנוסחה זו כדי למצוא את התנועה המתקבלת לכל תמסורת פלנטרית. בכללי:

כאשר:

• המהירות הזוויתית היא של הגג”ש הראשון בתמסורת.
• המהירות הזוויתית היא של הגג”ש האחרון בתמסורת.
• המהירות הזוויתית היא של הזרוע.

מספר הלוויינים הוא למעשה מספר הזרועות בהם מועבר העומס. לכן, קיים הרצון להגדיל ככל האפשר את מספר הלוויינים, אבל אנו מוגבלים במקום על התמסורת. הטבלה הבאה מציגה את מספר הלוויינים המומלץ.

מספר הלוויינים המומלץ לפי יחס ( בטבלה). (Klebanov & Groper, 2016).

תרגילים

תרגיל 1

יש לתכנן תשלובת בעלת יחס תמסורת כולל של כך שכיוון הסיבוב ביציאה מהתשלובת הפוך לזה שבכניסה לתשלובת. מספר השיניים המינימלי שניתן להשתמש בכל גג”ש הוא .

הערה:

נניח זווית לחץ של ולכן מספר שיניים מינימלי הוא . עבור זווית לחץ אחרת היינו מקבלים מספר שיניים מינימלי שונה. נושא זה יובהר בפרק הבא.

פתרון:
נבדוק שתי דרגות הפחתה:

נניח ששתי הדרגות ההפחתה זהות:

אם נניח שלושה דרגות הפחתה:

לכן נבחר תמסורת עם שלוש דרגות הפחתה.

יחס התמסורת שבחרנו הוא לכל דרגה, ונדרש מינימום שיניים. אז נבחר שיניים לפיניון ונבדוק האם בגיר יש מספר שיניים שלם:

קיבלנו מספר שיניים לא שלם עבור שיניים בפיניון וכך גם עבור שיניים. עבור שיניים בפיניון נקבל שיניים בגיר, שנעגלו ל-.

לסיכום, נבחר בתמסורת המכילה שלושה דרגות הפחתה עם גלגלי שיניים ומספר שיניים כלהלן:

נקבל שיחס התמסורת הוא:

שזה סטייה של .
אם נרצה פתרון מדויק, נוכל לבחור דרגות הפחתה עם יחס תמסורת לא זהה:

ואת מספר השיניים נבחר בהתאם:

תרגיל 2

יש לתכנן תשלובת בעלת יחס תמסורת של כאשר נדרש שציר הכניסה לתשלובת וציר היציאה מהתשלובת יסתובבו באותו הכיוון ויהיו קו-אקסיאליים. מספר השיניים המינימלי האפשרי לתכנון בגג”שים הוא .

פתרון:
נבחר שתי דרגות הפחתה על מנת שכיוון הסיבוב של היציאה יהיה זהה לכניסה. נדרש גם יחס תמסורת של , לכן נבחר שתי דרגות הפחתה עם יחס תמסורת של ו-:

מכאן נגיע לקשרים:

מאילוץ קו-אקסיליות על מספר השיניים:

נציב את הקשרים:

אם נבחר , נקבל שמספר השיניים יהיה קטן מ-, ולכן נבחר , כך ש:

איור להמחשה.

תרגיל 3

נתונה הממסרת הפלנטרית שבציור. דרוש למצוא את מהירות הסיבוב של הזר (הטבעת) כאשר מהירויות השמש והזרוע הן בכיוון השעון ו- בכיוון השעון בהתאמה. מספר השיניים נתונים באיור.

סכמת התמסורת.

פתרון:
נסמן את גג”ש השמש ככניסה , ואת גג”ש הזר כיציאה .
נחשב את באמצעות מכפלת השיניים:

נחשב את ע”י שימוש במהירויות הסיבוב:

נשווה את שני הביטויים ל- ונקבל:

→ קודם: MDN1_005הבא: MDN1_007 ←