פנגייה

MDN1_007 פרופיל השן

• זמן קריאה: 14 דק'

מונחים בגג”שים ישרים

באיור הבא מוצגים השיניים של גלגל שיניים ישר:
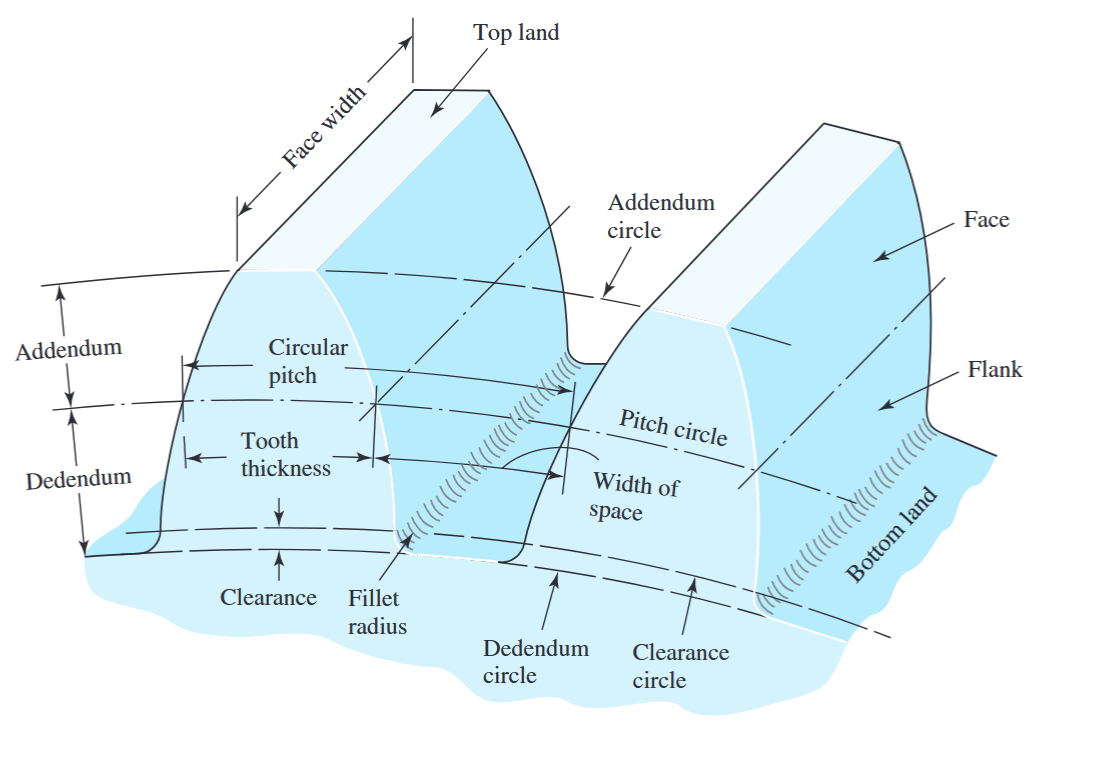
bookhue

מונחי יסוד בגלגל שיניים ישר. (Budynas et al., 2015).

  • מעגל הפסיעה/חלוקה (pitch circle) הוא העיגול עליו אנו מבססים את החישובים. הקוטר שלו הוא קוטר הפסיעה/החלוקה (pitch diameter) . המעגלי פסיעה של זוג גלגלי שיניים המשולבים אחד בשני משיקים אחד לשני. הפיניון (pinion) הוא הקטן משני הגלגלי שיניים. הגדול יותר נקרא גיר (gear).
  • הפסיעה ההיקפית (circular pitch) היא המרחק הנמדד על מעגל החלוקה מנקודה אחת על השן לנקודה זהה על גבי השן השכנה. לכן הפסיעה ההיקפית שווה לסכום עובי השן (tooth thickness) והמרווח בין השיניים (width of space).
  • המודול (module) הוא היחס בין קוטר החלוקה למספר השיניים . גודל המודול קובע את ממדי השיניים והוא הבסיס לבניית כלים לעיבוד גלגלי השיניים.
  • גובה ראש השן (addendum) הוא המרחק הרדיאלי בין קצה עליון של השן למעגל החלוקה.
  • גובה עיקר השן (dedendum) הוא המרחק הרדיאלי בין קצה התחתון של השן ומעגל החלוקה.
  • גובה השן הוא ההפרש בין המעגל הראשי (addendum circle) והמעגל העיקרי (dedendum circle):
  • מרווח (clearance) הוא ההפרש שבין גובה ראש השן לגובה עיקר השן:
  • פסיעה קטרית (diametral pitch) :
  • מ-(SH13-3) ו-(SH13-1) אנו גם יכולים לרשום:

עובי השן בגג”ש סטנדרטיים מקיים:

באופן כללי, אם השן לא סטנדרטית (או אם למשל יש חוסר התאמה בין מרכזי הגג”שים) ניתן להראות מגאומטרייה ש:

כאשר:

  • הפסיעה היא הפסיעה ההיקפית ה”ישנה”, הסטנדרטית.
  • הזווית היא זווית הלחץ ה-”חדשה”.
  • הזווית היא זווית הלחץ ה-”ישנה”, הסטנדרטית.
  • הפונקציה היא פונקציית האבולונט, המוגדרת:
  • הרדיוס הוא הרדיוס ה-”חדש” שבו מודדים את עובי השן:
  • הרדיוס הוא רדיוס ה-”ישן”, הסטנדרטי, בו מודדים את עובי השן:

פעולה מצומדת

נניח כעת שהשיניים נוצרו באופן מושלם, חלקים וקשיחים לחלוטין. בעולם האמיתי כמובן יהיה דפורמציות.
כאשר מתכננים את פרופיל השן, אנו רוצים שיחס המהירויות הזוויתיות בין שתי שיניים יהיה קבוע. לאופן פעולה זה אנו קוראים פעולה מצומדת. באופן תאורטי, נוכל לבחור שרירותית כל פרופיל שן אקראי ולו להצמיד פרופיל שן אחר שביחד יקיימו פעולה מצומדת. אחד מהפתרונות האלה נקרא פרופיל אֵבוֹלְוֵנְט (involute profile).

כאשר משטח עקום כללי דוחף משטח עקום כללי אחר, נקודת המגע ביניהם נמצאת בנקודה בה שני המשטחים משיקים אחד לשני (נקודה באיור), והכוחות הפועלים בכל רגע בכיוון הנורמל לשני המשטחים. הקו נקרא קו הפעולה. קו פעולה זה יחתוך את קו המרכזים בנקודה כלשהי . המהירות הזוויתית בין שתי הזרועות פרופורציונית בהפוך לרדיוס שלהם לנקודה . המעגלים המשורטטים דרך נקודה מכל מרכז נקראים מעגלי פסיעה, והרדיוס שלהם רדיוס פסיעה. הנקודה נקראת נקודת הפסיעה.

כדי להעביר תנועה במהירות זוויתית קבועה, נקודת הפסיעה חייבת להישאר קבועה - כי אם היא לא קבועה, אז רדיוסי הפסיעות לא קבועות, ואז היחס ביניהם לא קבוע, ואז המהירות הזוויתית ביניהם לא קבועה. לכן, כל קווי הפעולה בכל רגע נתון של מגע, חייבים לעבור דרך אותה הנקודה . ניתן להראות שבפרופילים אבולונטים, תכונה זו מתקיימת.

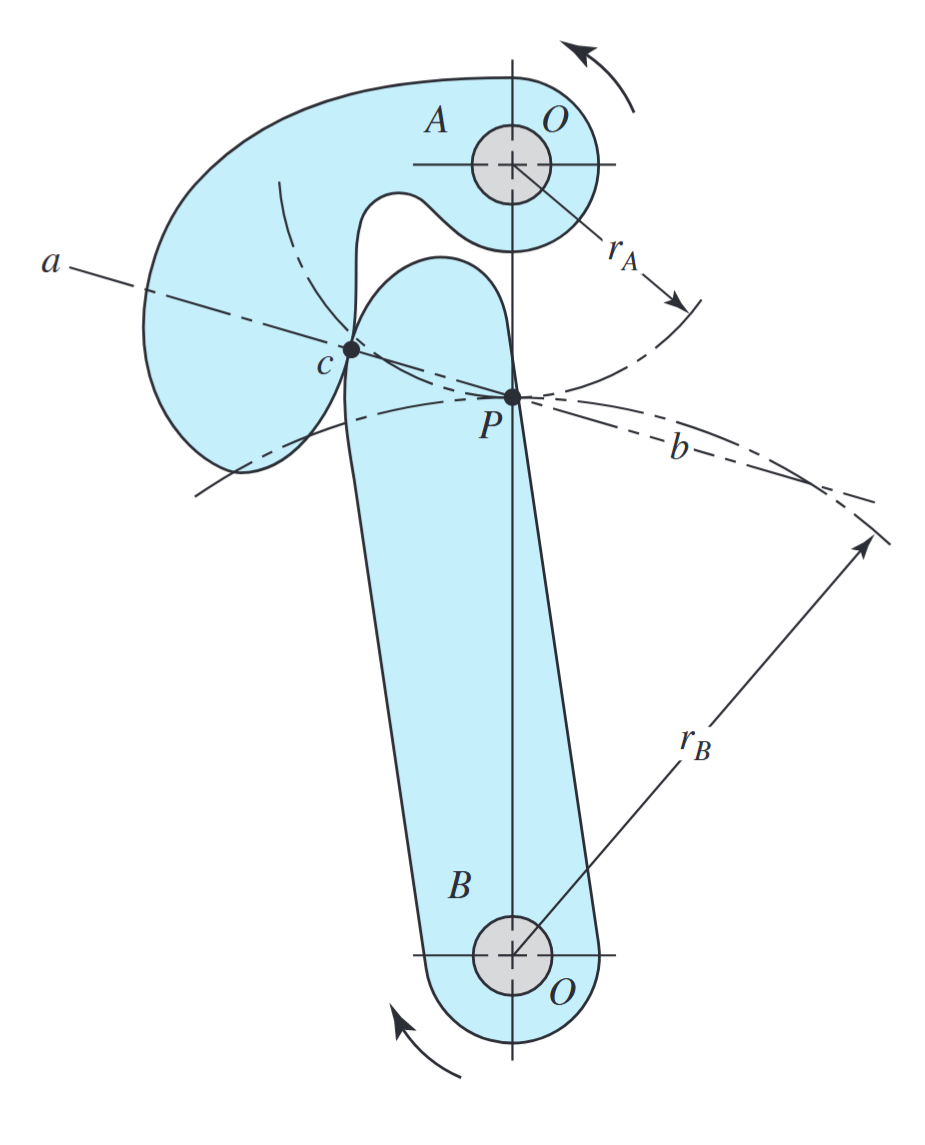
bookhue

שני משטחים עקומים במגע. (Budynas et al., 2015).

מאפייני האבולונט

נוכל לשרטט עקומה אבולונטית באופן המוצג באיור הבא:
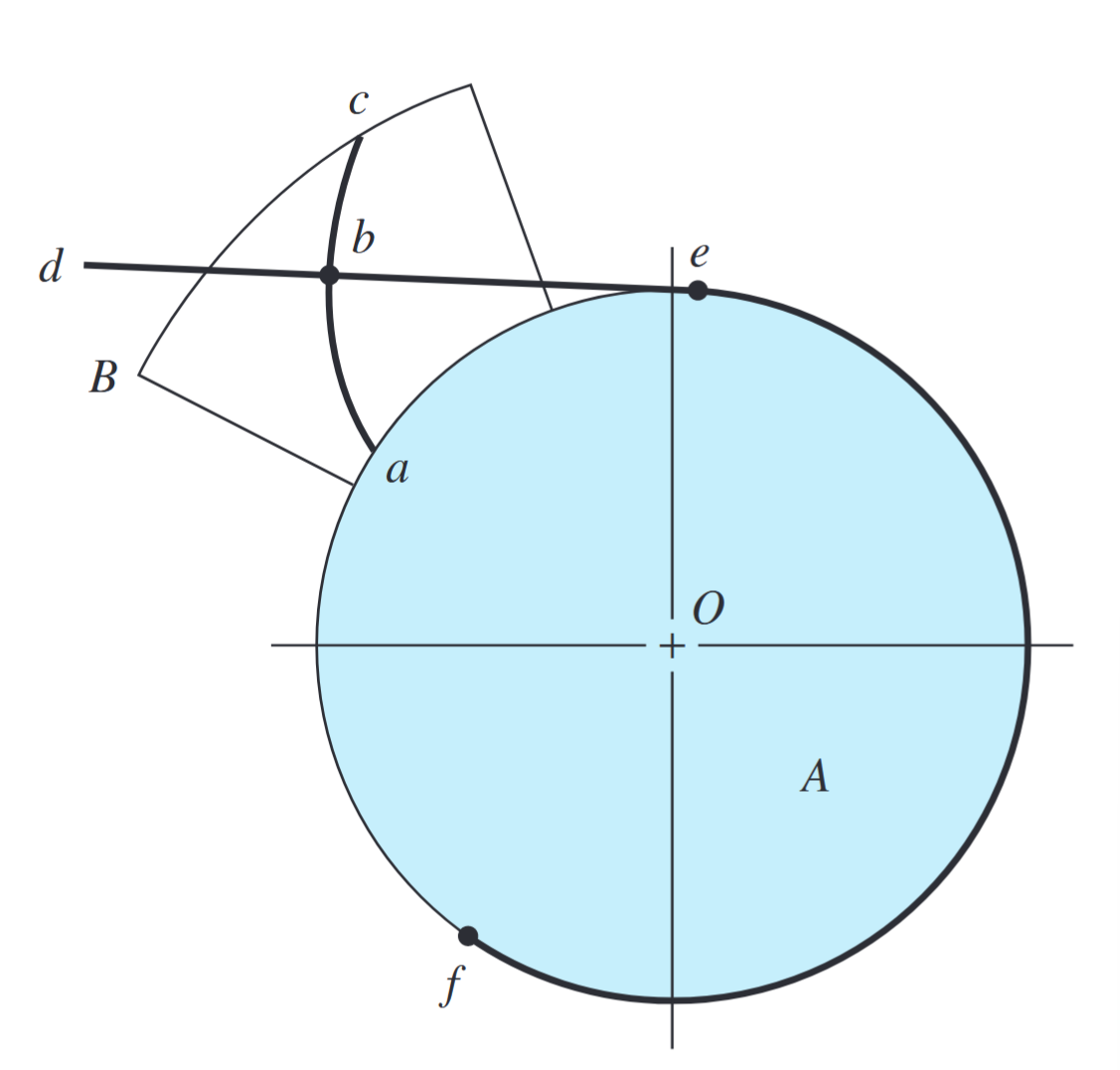
bookhue

יצירת אבולונט. (Budynas et al., 2015).

מצמידים לגליל גזרה , וסביב הגליל מותחים חוט , הנשאר מתוח. נקודה על החוט מייצגת את נקודת העקיבה, וכאשר החוט מלופף ומשוחרר מהגליל, נקודה תשאיר עקבה שהיא עקומת האבולונט . הרדיוס של העקמומיות של האבולונט משתנה ברציפות, כאשר הוא בנקודה ובמקסימום שלו בנקודה . בנקודה הרדיוס שווה לאורך , מארח והנקודה מסתובבת רגעית סביב נקודה . לכן, הקו נורמלי לאבולונט בכל נקודות החיתוך, ובאותו הזמן, משיק לגליל . המעגל עליו האבולונט משורטט נקרא מעגל הבסיס.
נראה כעת איך פרופיל האבולונט מקיים את מעבר התנועה במהירות זוויתית קבועה. באיור הבא, שני גלגלי שיניים עם מרכזים קבועים ו- משורטטים עם מעגלי בסיס שהרדיוסים שלהם הם ו- בהתאמה. כעת נדמיין שחוט מלופף עם כיוון השעון סביב מעגל הבסיס של גיר , ונמתח בין נקודות ו-, ומלופף נגד כיוון השעון סביב מעגל הבסיס של גיר .

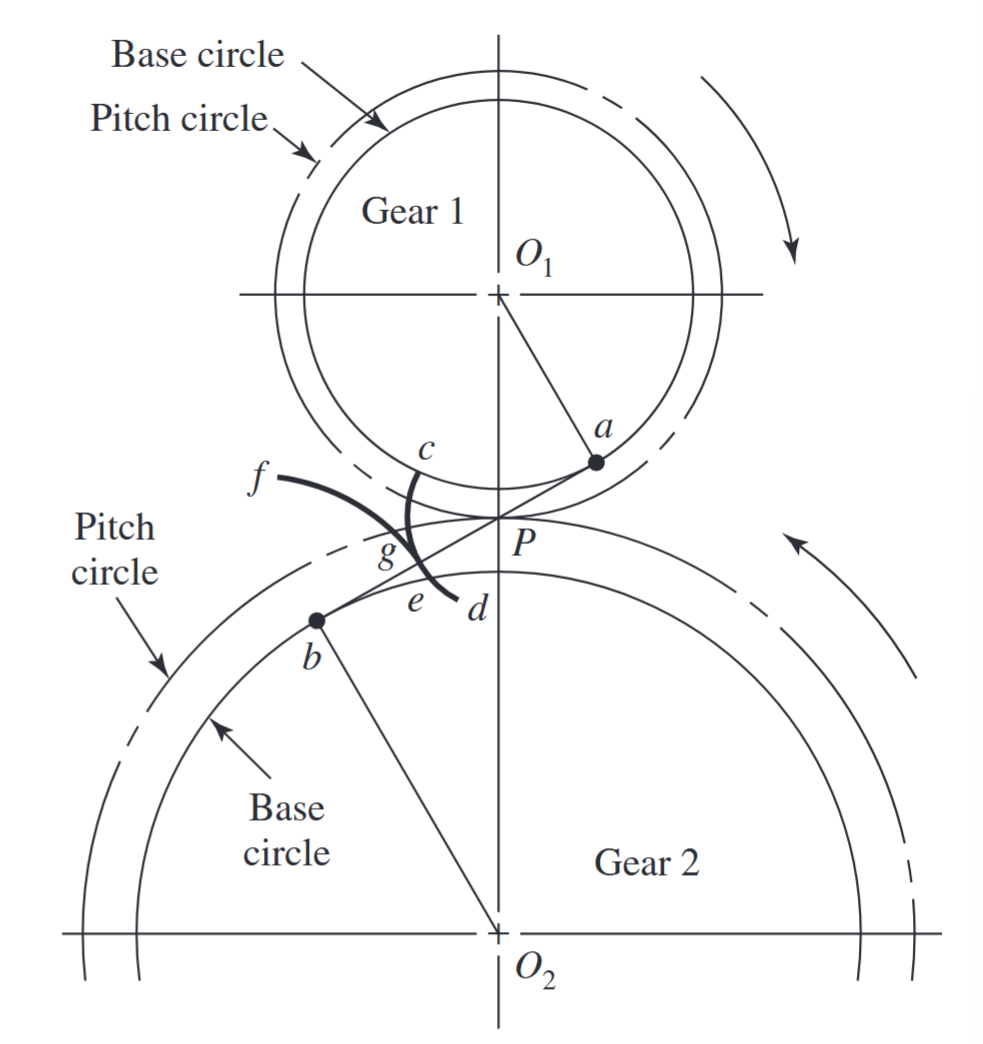
bookhue

פעולה אבולונטית. (Budynas et al., 2015).

אם, כעת, מעגלי הבסיס מסתובבים בכיוונים שונים, כדי שהחוט יישאר מתוח, נקודה על המיתר תיצור את העקבה על גיר ו- על גיר . נקודה העקבה, לפיכך, מייצגת את נקודת המגע, בעוד החלק של המיתר הוא קו הפעולה. נקודת המגע נעה לאורך קו הפעולה; קו הפעולה לא משנה את מיקומו, כי הוא תמיד משיק למעגלי הבסיס; ומאחר וקו הפעולה תמיד ניצב לאבולונטים בנקודה המגע, הדרישה של תנועה אחידה מתקיימת.

פרופיל השן

כדי להבין את אופן פעולה של השן, נעבור צעד צעד את התהליך של בניית שיניים על זוג גג”שים.
כאשר שני גג”שים משולבים, מעגלי הפסיעה שלהם יתגלגלו ללא החלקה אחד על השני. נסמן את הרדיוסי פסיעה שלהם כ- ו- והמהירויות הזוויתיות שלהם ב- ו-, בהתאמה. לכן, מהירות קו הפסיעה הוא:

והקשר בין הרדיוסים והמהירויות הזוויתיות הם:

כעת נניח שאנו רוצים לתכנן מפחית מהירות כך שמהירות הכניסה היא ומהירות היציאה היא . זהו יחס של , מה שאומר ממשוואה (SH13-5) שהיחס בין הקטרי פסיעה שלהם יהיה זהה. הממדים השונים בגג”שים תמיד מתבססים על מעגלי הפסיעה שלהם. נניח ואנו רוצים פיניון ב- שיניים עם גיר ב- שיניים, עם קטרי פסיעה ו- , בהתאמה.

השלב הראשון בשרטוט השיניים על זוג גג”שים משולבים מתואר באיור הבא:
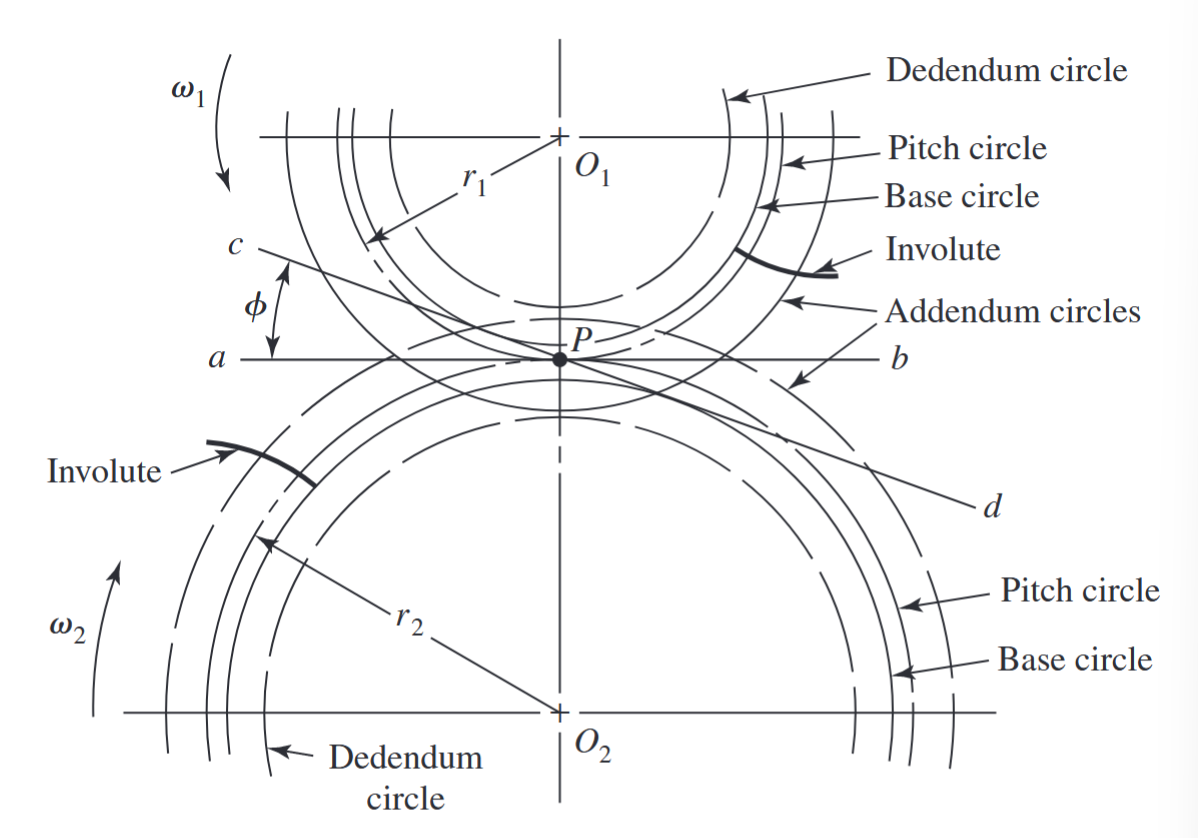
bookhue

מעגלים בגיר. וואו המון קווים. (Budynas et al., 2015).

המרחק בין המרכזים הוא סכום רדיוסי הפסיעה, אז במקרה שלנו הוא . לאחר מכן, נבנה את המעגלי פסיעה ברדיוסים ו-. הם משיקים ל-, נקודה הפסיעה. לאחר מכן נשרטט את קו , המשיק המשותף, דרך . נחליט שגיר הוא המניע, ומאחר והוא מסתובב נגד כיוון השעון, נשרטט את קו דרך נקודה בזווית למשיק המשותף . לקו שלושה שמות - קו הלחץ, הקו היוצר, וקו הפעולה. הוא מייצג את הכיוון בו הכוח פועל בין הגג”שים.
הזווית נקראת זווית הלחץ, והערך שלה הוא לרוב עד . לאחר מכן, על כל גג”ש נשרטט מעגל המשיק לקו הלחץ. מעגלים אלו הם מעגלי הבסיס. מאחר והם משיקים לקו הלחץ, זווית הלחץ קובעת את גודלם. כפי שניתן לראות באיור הבא, הרדיוס של מעגל הבסיס הוא:

כאשר הוא רדיוס הפסיעה.
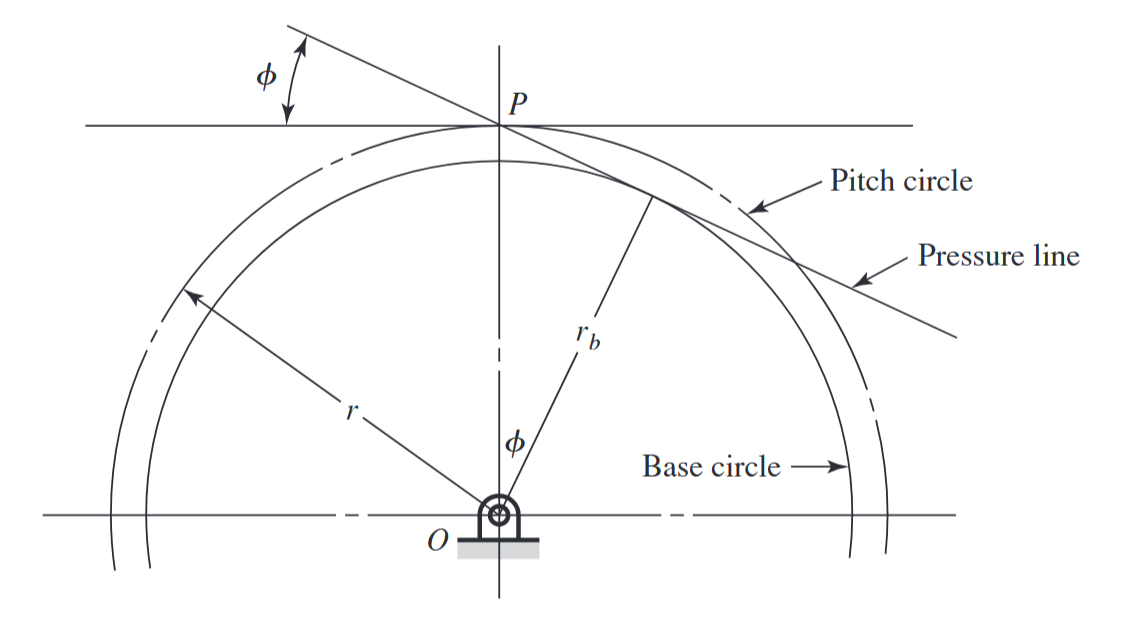
bookhue

רדיוסי מעגלי הבסיס תלויים בזווית הלחץ . (Budynas et al., 2015).

כעת, נשרטט אבולונט על מעגל הבסיס. בעזרת אבולונט נבנה צד אחד של שן בגיר. גובה ראש השן וגובה עיקר השן. לפי משוואה (SH13-2) ואופן הגדרת הגבהים:

בעזרת גבהים אלו נוכל לשרטט את המעגל הראשי והמעגל העיקרי.
לפי משוואה (SH13-3), הפסיעה היא:

ולכן עובי השן הוא:

המרווח שלנו יהיה:

נקבל משהו מהצורה:
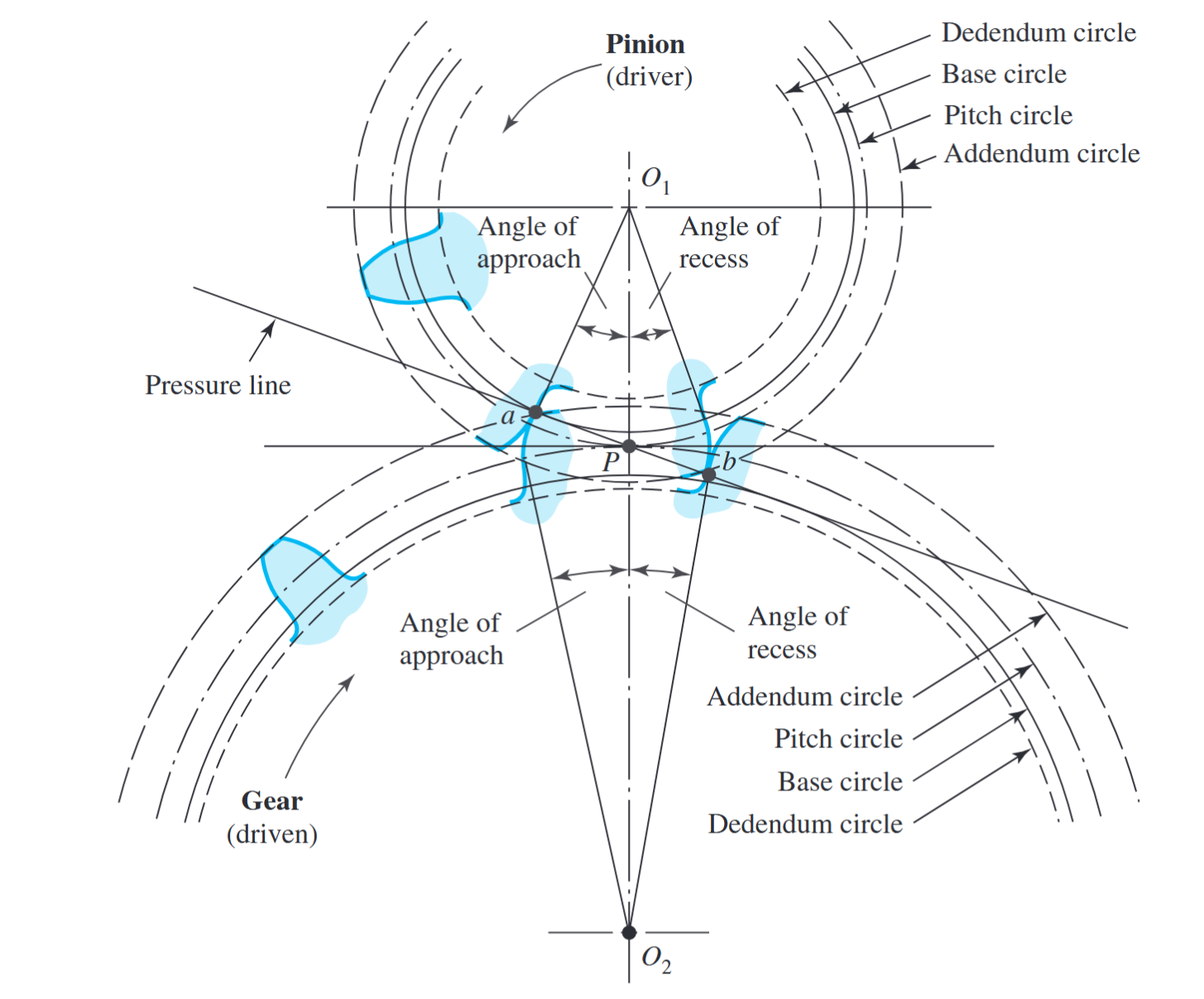
bookhue

אופן פעולת השן. (Budynas et al., 2015).

באיור לעיל, הפיניון עם המרכז הוא המניע והוא מסתובב נגד כיוון השעון. קו הפעולה (או קו הלחץ, הקו היוצר) זהה למיתר שאיתו נעזרנו לבנות את קו האבולונט במאפייני האבולונט. המגע מתרחש לאורך קו זה. הזווית בין קו מרכז הגלגלים לנקודת המגע , שזו הנקודה בה המעגל הראשי של הגג”ש ה-מונע חותך את קו הפעולה, נקראת זווית הכניסה (angle of approach). באותו אופן, הזווית בין קו מרכז הגלגלים לנקודת היציאה , שזו הנקודה בה המעגל הראשי של הגג”ש ה-מניע חותך את קו הפעולה, נקראת זווית היציאה (angle of recess).

יחס מגע

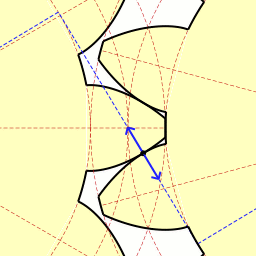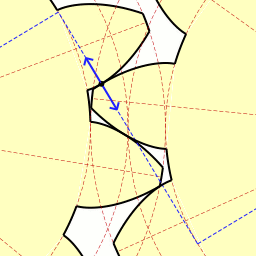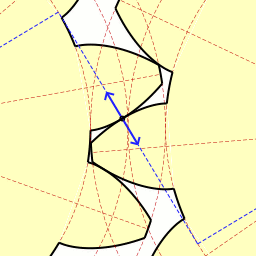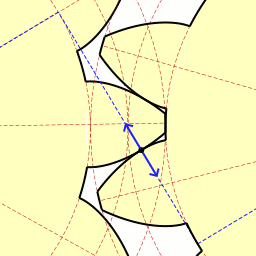
bookhue

שני גג”שים אבולונטים. השמאלי מניע את הימני. (Wikipedia).

אזור הפעולה של גג”שים משולבים מתואר באיור הבא:
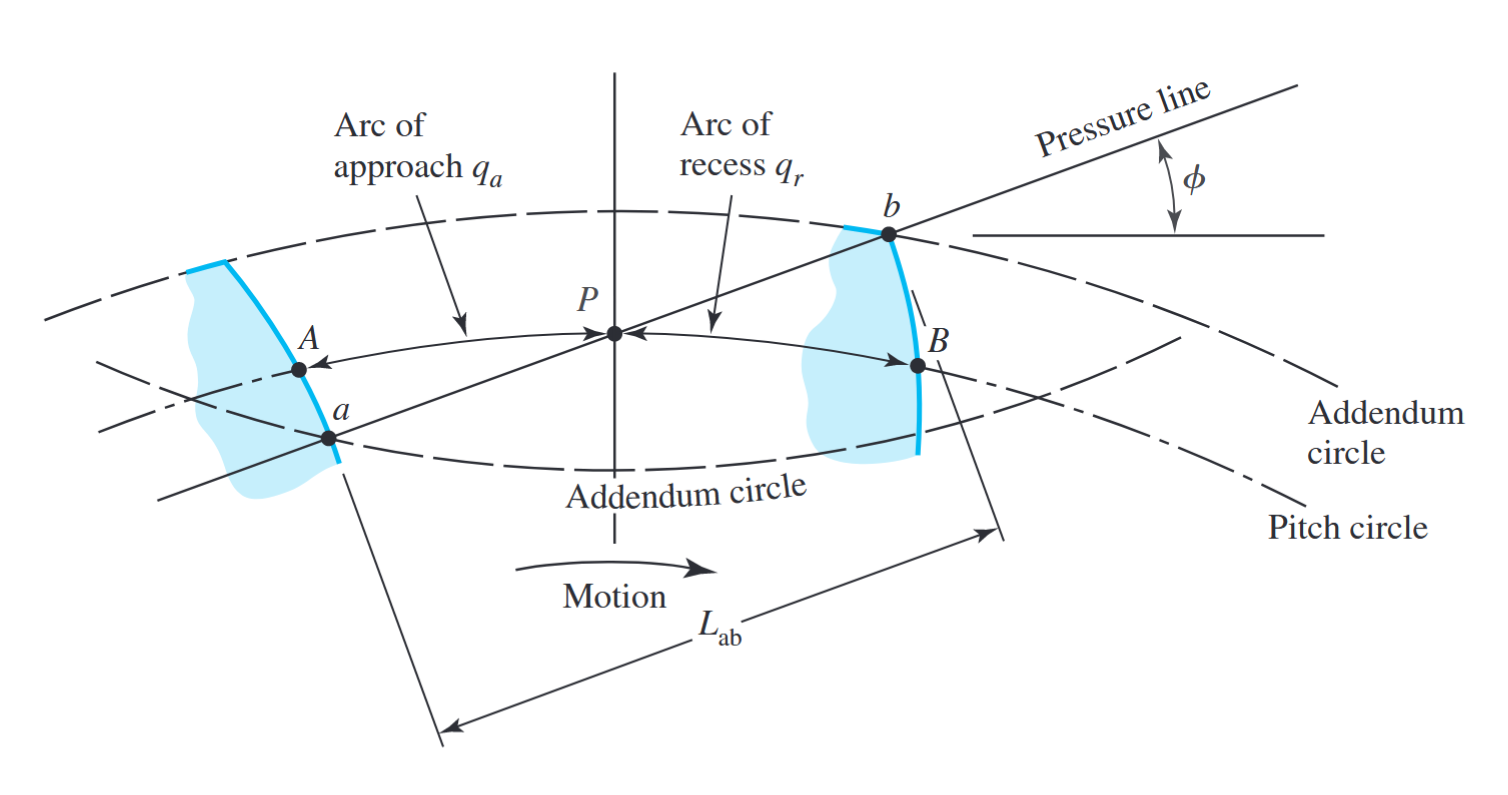
bookhue

הגדרת יחס המגע. (Budynas et al., 2015).

המגע בין השיניים מתחיל ומסתיים בחיתוכים בין שתי המעגלים הראשיים (של שתי הגג”שים השונים) עם קו הלחץ. באיור לעיל מגע מתחיל ב- ומסתיים ב-. פרופילי השן המשורטטים דרך נקודות אלו חותכים את מעגל הפסיעה בנקודות ו-, בהתאמה.
כפי שניתן לראות באיור, המרחק נקרא קשת הכניסה , והמרחק קשת היציאה . סכום הקשתות נקרא קשת המגע - .
כעת, נתייחס למקרה בו קשת הפעולה שווה בדיוק לפסיעה - . זה אומר ששן אחת והמרווח בין שתי שיניים יתפוס את כל אורך הקשת . במילים אחרות, כאשר שן רק מתחילה מגע ב-, השן הקודמת בדיוק מסיימת מגע ב-. לכן, במהלך התנועה מ- ל-, תמיד יהיה בדיוק זוג שיניים אחד במגע.
בנוסף, נתייחס למקרה בו קשת הפעולה גדולה מהפסיעה, למשל . זה אומר שכאשר זוג שיניים אחד בדיוק נכנס למגע ב-, עוד זוג שיניים עדיין נמצא במגע, כי הוא עדיין לא הגיע ל-. לכן, לזמן קצר, יהיו שתי שיניים במגע, אחת בקרבת והשנייה בקרבת .
בגלל טבע פעולת השיניים, תמיד יש זוג אחד או שניים של שיניים במגע, ונהוג להגדיר את יחס המגע כ:

כמספר המתאר את מספר השיניים הממוצע במגע. לרוב לא נרצה לתכנן שיניים עם יחס מגע הקטן מ-, כי אי-דקויות בהתקנת הגלגלי שיניים עלול להוריד את יחס המגע עוד יותר.
דרך יותר טובה לחישוב היחס מגע היא למדוד את אורך קו המגע במקום הקשת . אם אורך קו הפעולה הוא , ניתן להראות שיחס המגע/מקדם השילוב הוא:

לפעמים נרצה לעבוד עם קירוב, רק כשיעור ראשוני לבחירת מספר שיניים:

מתוך גאומטרייה, ניתן להראות שאורך קו הפעולה הוא:

כאשר הוא המרחק בין מרכז הגלגלי שיניים, הוא רדיוס הפיניון, ו- הוא רדיוס הגיר.

הפרעה בגלגל שיניים

המגע של אזורים בפרופילי השן שלא מצומדים נקרא הפרעה (interference). באיור הבא משורטטים שני גלגלי שיניים עם זווית לחץ (שכבר לא בשימוש). המניע, גיר , מסתובב עם כיוון השעון.
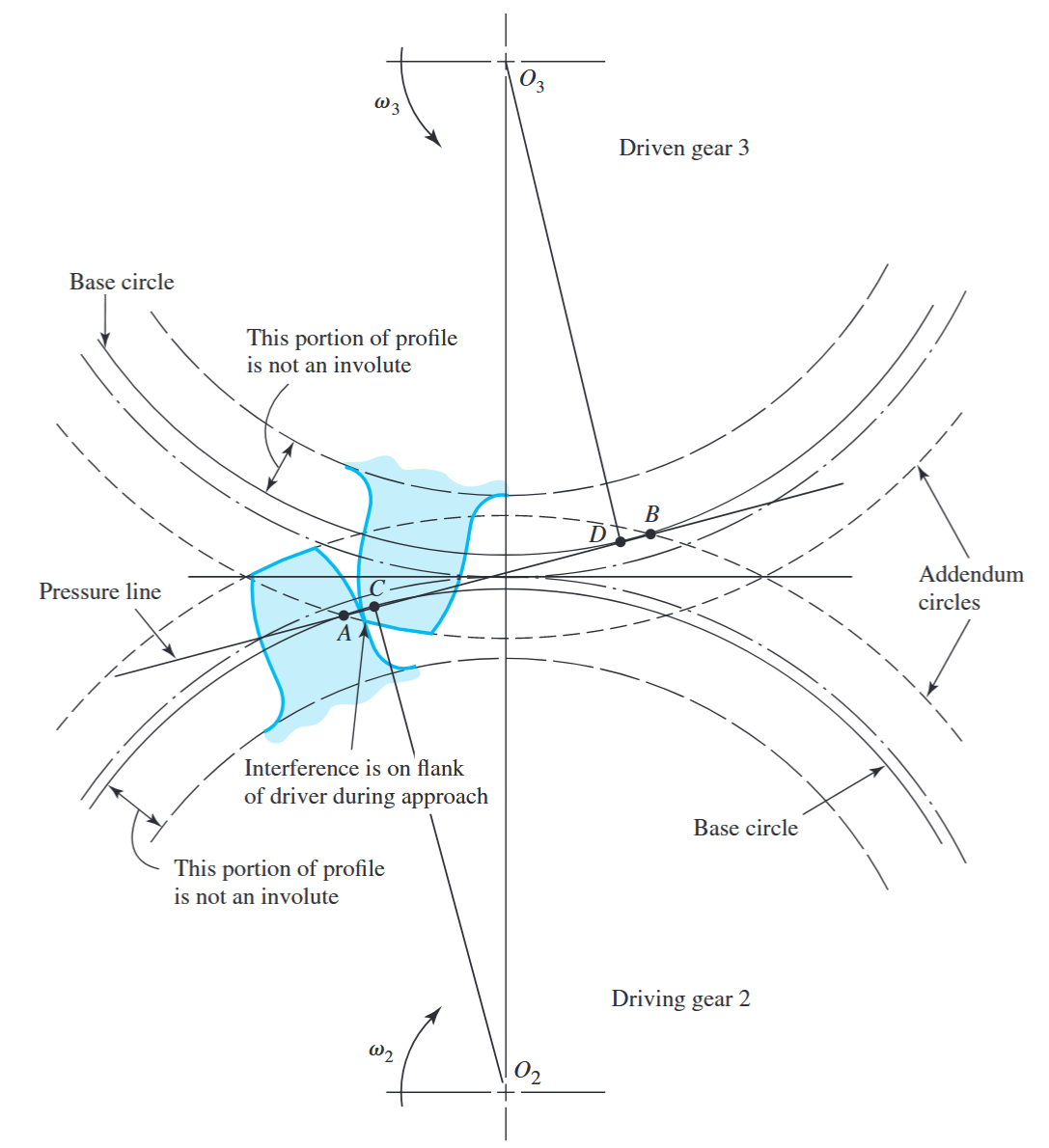
bookhue

הפרעה בפעולת השיניים. (Budynas et al., 2015).

נשים לב שנקודות ההשקה של קו הלחץ עם מעגל הבסיס ו- ממוקמות בתוך נקודות ו- - שהן נקודות תחילת המגע וסוף המגע, בהתאמה. לפיכך, מתקיימת הפרעה.
נסביר כעת את ההפרעה. מגע מתחיל כאשר הקצה של השן המונעת באה למגע עם גב השן של השן המניעה. במקרה זה גב השן המניעה קודם מקיימת מגע עם השן המונעת בנקודה , וזה מתרחש לפני שהאזור האבולונטי של השן המניעה מגיע למגע. במילים אחרות, המגע מתרחש מתחת למעגל הבסיס של גיר , על האזור לא אבולונטי של גב השן. התוצאה של תופעה זו היא שהקצה האבולונטי או פני השן המונעת נוטה לחפור את הגב הלא אבולונטי של השן המניעה.
כאשר מייצרים את הגלגלי שיניים, ההפרעה נמנעת באופן אוטומטי כי הסכין חותכת גם את אזור ההפרעה בגב השן. לתופעה זו קוראים undercutting; אבל, אם יש undercutting, השן שנחתכה מוחלשת באופן משמעותי. לכן, כאשר אנו מבצעים undercutting, אנו פשוט מחליפים בעיה אחת עם בעיה אחרת.

מספר השיניים הכי נמוך על פיניון וגיר ישר, ביחס תמסורת של , שיכול להתקיים ללא הפרעה הוא . מספר שיניים זה לשיניים ישרות נתון ע”י:

כאשר לשיניים בעומק מלא (full depth teeth) ו- לשיניים מקוצרות (stub teeth).
לזווית לחץ שהיא , עם , זה הופך ל-. לכן, הוא מספר השיניים המינימלי לגיר ופיניון ישרים כדי שלא תהיה הפרעה. לזווית לחץ זה יוצא , ולכן זוהי זווית לחץ שפחות בשימוש.

אם לגיר יש יותר שיניים מלפיניון, כאשר , אז מספר השיניים המינימלי על הפיניון ללא הפרעה נתון ע”י:

הגיר הכי גדול עבור פיניון נתון שהוא ללא הפרעה הוא:

הפיניון הישר הכי קטן שיתפקד על פס-שיניים (gear rack) ללא הפרעה הוא:

  • ניתן למנוע את תופעת ההפרעה ע”י הגדלת מספר השיניים בפיניון. עם זאת, הגדלת כמות השיניים בפיניון תגדיל את קוטר הפסיעה .
  • ניתן למנוע את תופעת ההפרעה ע”י הגדלת זווית הלחץ, אבל הגדלת תגרור מעגל בסיס יותר קטן.

תרגילים

תרגיל 1

נתונה מערכת גג”ש בעלת שיניים בגלגל המניע. המרחק בין שני מרכזי הגג”שים הוא . זווית הלחץ היא והמודול הוא .

סעיף א’

יש לחשב את הגדלים הבאים:

  1. הפסיעה ההיקפית.
  2. מספר השיניים בגלגל המונע.
  3. יחס התמסורת.
  4. רדיוסי הבסיס.

פתרון:
את הפסיעה ההיקפית נוכל למצוא מהגדרת המודול:

מבחינת מספרי השיניים בגלגל המונע , מתקיים הקשר הבא:

ולכן:

מבחינת רדיוסי הבסיס, באמצעות זווית הלחץ ורדיוס החלוקה, ממשוואה (SH13-6):

(עם עבור base).
מכאן:

מבחינת יחס התמסורת:

סעיף ב’

עקב טעות במיקום ציר הגיר, גדל המרחק בין שני מרכזי הגג”שים ל- . יש לחשב כעת את הגדלים הבאים:

  1. קוטרי החלוקה החדשים.
  2. המודול החדש.
  3. זווית הלחץ החדשה.

פתרון:
הגדלים שהשתנו הם קטרי החלוקה, המודול, וזווית הלחץ. הגדלים שלא השתנו (כי הם גדלים הקשורים לגודל הפיזי של השיניים עצמן) הם רדיוסי הבסיס, יחס התמסורת ומספר השיניים בכל גג”ש.

נתון כעת כי:

נסמן את קטרי החלוקה החדשים ב- וב-. נמצא אותם בעזרת יחס התמסורת (שנשאר קבוע) ובעזרת המרחק בין מרכזי הגג”שים:

מפתרון שתי המשוואות נקבל:

המודול החדש הוא מחושב גם כן לפי הגדרה:

כיוון שרדיוסי הבסיס לא השתנו:

תרגיל 2

נתון כי ו-. יש לחשב את אורך קו המגע ואת יחס המגע .

פתרון:
לחישוב אורך המגע, ראשית נחשב את רדיוסי מעגלי החלוקה של הפיניון והגיר. לצורך כך נשתמש בהגדרת המודול:

לאחר הצבת נתונים נקבל:

נציב את הנתונים לנוסחת אורך המגע:

לכן יחס המגע:

נציב נתונים ונקבל:

תרגיל 3

נתון גג”ש בעל פרופיל אבולונטי עם רדיוס חלוקה , זווית לחץ ורדיוס מעגל בסיס .
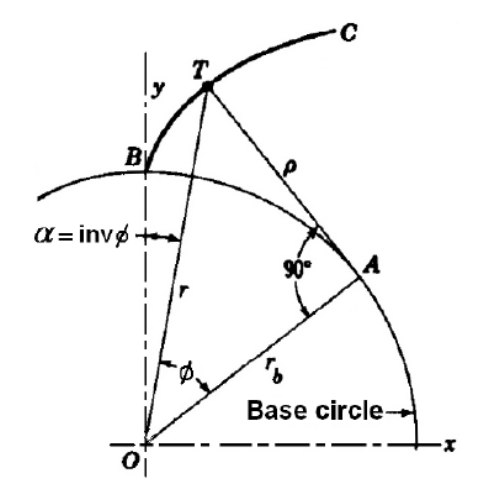
bookhue

סכמת הגג”ש.

יש לחשב את הזווית המוגדרת ע”י הנקודות הבאות:

  1. מרכז מעגל הבסיס (נקודה ).
  2. נקודת חיתוך מעגל החלוקה עם עקומת האבולונט (נקודה ).
  3. נקודת חיתוך מעגל הבסיס עם עקומת האבולונט (נקודה ).

פתרון:
כיוון שהנקודה נמצאת על עקומת האבולונט, אורך המיתר שווה לאורך הקשת .

את אורך הקשת ניתן לחשב באמצעות (אם הזוויות נתונות ברדיאנים). מצד שני את אורך המיתר ניתן לחשב באמצעות . מהשוואת הביטויים נקבל:

הערות:

  1. ניתן לחשב את זווית הלחץ לכל נקודה על הפרופיל האבולונטי ולאו דווקא למעגל החלוקה. במקרה הכללי זווית הלחץ תסומן ב-.
  2. יש להקפיד לעבוד ברדיאנים עבור חישובי זוויות.
  3. באם נתונה זווית הלחץ ניתן לחשב את פונקציית האבולונט שלה מתוך טבלאות או לחשב את פונקציית האבולונט שלה באופן ישיר.
  4. באם נתונה פונקציית האבולונט של זווית הלחץ, ניתן לחשב את זווית הלחץ עצמה מתוך הטבלאות או לחשב את זווית הלחץ באופן נומרי.

תרגיל 4

שני גלגלי שיניים בעלי שיניים ישרות וזווית לחץ נמצאים בשילוב כמתואר באיור. לגלגלי השיניים מודול השווה ל- והמרחק בין הצירים . יחס התמסורת .

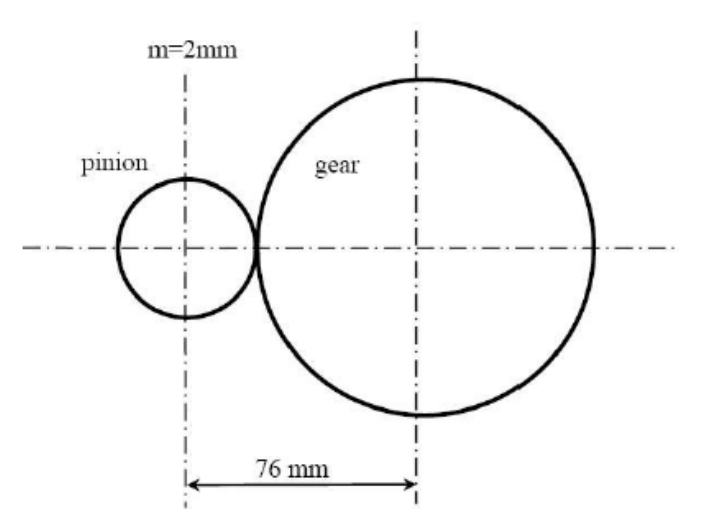
bookhue

סכמת הגג”שים.

סעיף א’

מהו יחס המגע?

פתרון:
ע”פ יחס התמסורת והמרחק בין המרכזים, נמצא את רדיוסי הגיר והפיניון:

נציב את רדיוסים אלו בנוסחה לחישוב אורך המגע:

נציב ביחס המגע:

נקבל:

סעיף ב’

האם צפויה תופעת undercutting בפיניון? דרושה הוכחה גאומטרית מלאה.

פתרון:
נשרטט את מעגל הבסיס, החלוקה, ומעגל הראשי לגיר ולפיניון. נסמן את נקודת החיתוך של מעגל הבסיס של הפיניון עם הקו הלחץ ב- ואת נקודת החיתוך של מעגל הבסיס של הגיר עם קו הלחץ ב-. באופן דומה, נסמן ב- ו- את נקודות החיתוך של רדיוסי המעגל הראשי של הפיניון ושל הגיר, בהתאמה, עם קו הלחץ.
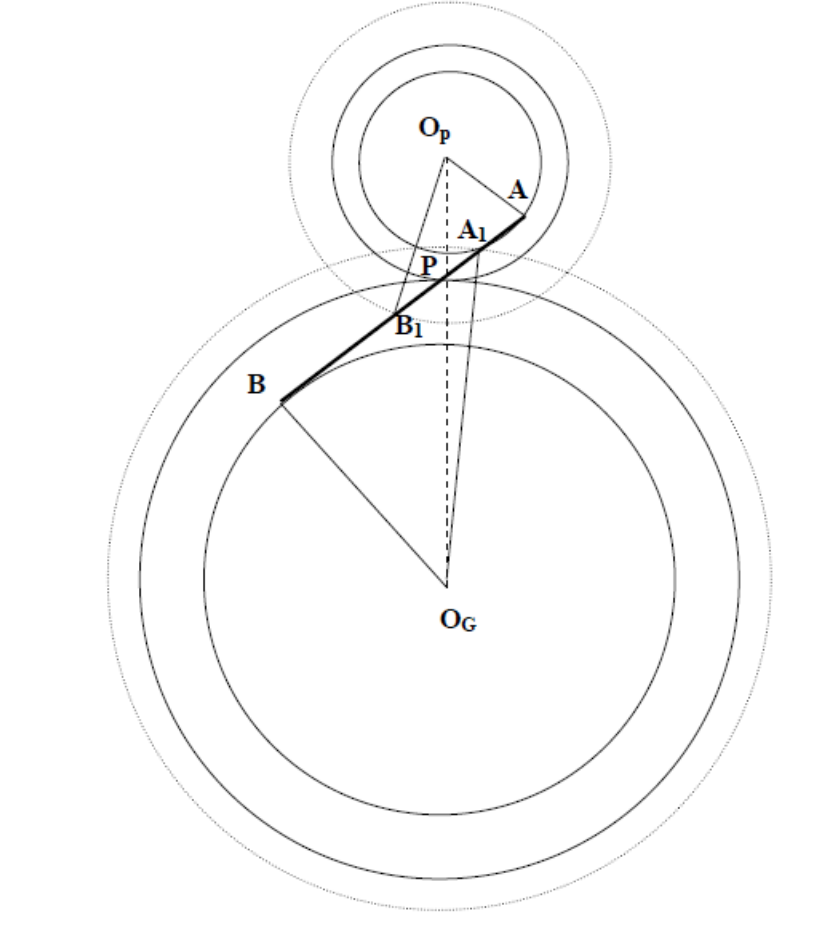
bookhue

גאומטריית הגג”שים.

למניעת תופעת ה-undercutting בפיניון, יש לדאוג כי הנקודה תהיה בין נקודה לנקודה (נקודת ההשקה שבין מעגלי החלוקה). כלומר: . נחשב כל אחד מהגדלים הנ”ל:

לגבי נצטרך טיפה יותר גאומטרייה:

ניתן לראות כי מתקיים ולכן לא צפויה תופעת undercutting בפיניון.

סעיף ג’

עבור יחס תמסורת וזווית לחץ נתונים, מצא קשר אלגברי כללי למספר השיניים המינימלי בו לא תהיה תופעת undercutting בפיניון.

פתרון:
ראינו בסעיף קודם שלמניעת undercutting בפיניון נדרש . נכתוב את התנאי באופן מפורש:

נעביר אגפים, נעלה בריבוע, ונזכור כי , ונקבל:

כמו כן מתקיים כי , ולכן:

נפתור את אי השוויון (שהוא פרבולה), ונמצא כי יש שתי פתרונות, אחד מהם שלילי ולכן לא פיזיקלי. הפתרון החיובי יהיה:

עמודים המציינים את העמוד הזה