פנגייה

MDN1_008 כוחות שילוב ומאמצי מגע בשן

• זמן קריאה: 23 דק'

ניתוח כוחות - גג”ש ישרות

נתחיל במוסכמות לגבי הסימונים. נתחיל בסימון עבור מסגרת המכונה, עבור הפיניון, ואת הגג”שים הבאים ב- וכו’. מבחינת גלים, אנו נסמן אותם ב- וכו’. עם מוסכמה זאת נסמן את הכוח המופעל ע”י גיר על גיר כ-. הכוח של גיר על גל הוא .

ניתן לסכם את הכוחות הפועלים על גיר למשל באופן הבא:
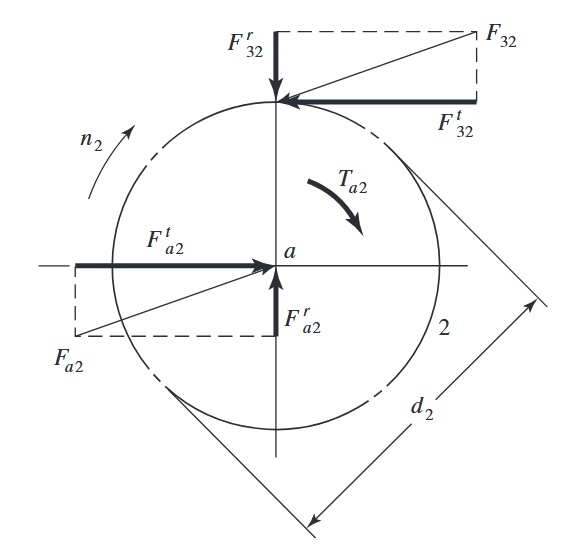
bookhue

עומסים הפועלים על גיר. (Budynas et al., 2015).

נסמן

ונקרא לו העומס המועבר. כוח משיקי זה נותן לנו את רוב המידע שאנו צריכים, הרי הכוח הרדיאלי לא באמת תורם לפעול התמסורת. המומנט פיתול שנותר כתוצאה מכוח משיקי זה הוא:

נוכל לחשב את ההספק המועבר דרך הגיר פשוט ע”י הכפלת מומנט הפיתול במהירות הזוויתית :

לכן, אם אנו עובדים ביחידות סטנדרטיות לקטלוגים, נוכל לרשום:

כאשר:

  • העומס הוא הכוח המשיקי המועבר ב-.
  • ההספק , ב-.
  • הקוטר של הגיר, ב-.
  • המהירות הזוויתית , ב-.

יותר נוח להציב לפעמים את הנוסחה:

משוואת הכפיפה של לואיס

ווילפרד לואיס היא הראשון שהגדיר משוואה לשיעור המאמצים בשיני גלגלי שיניים. עקרון הפיתוח שלו התבסס על ההנחה שלו שהשן מתפקדת כמו קורה רתומה:

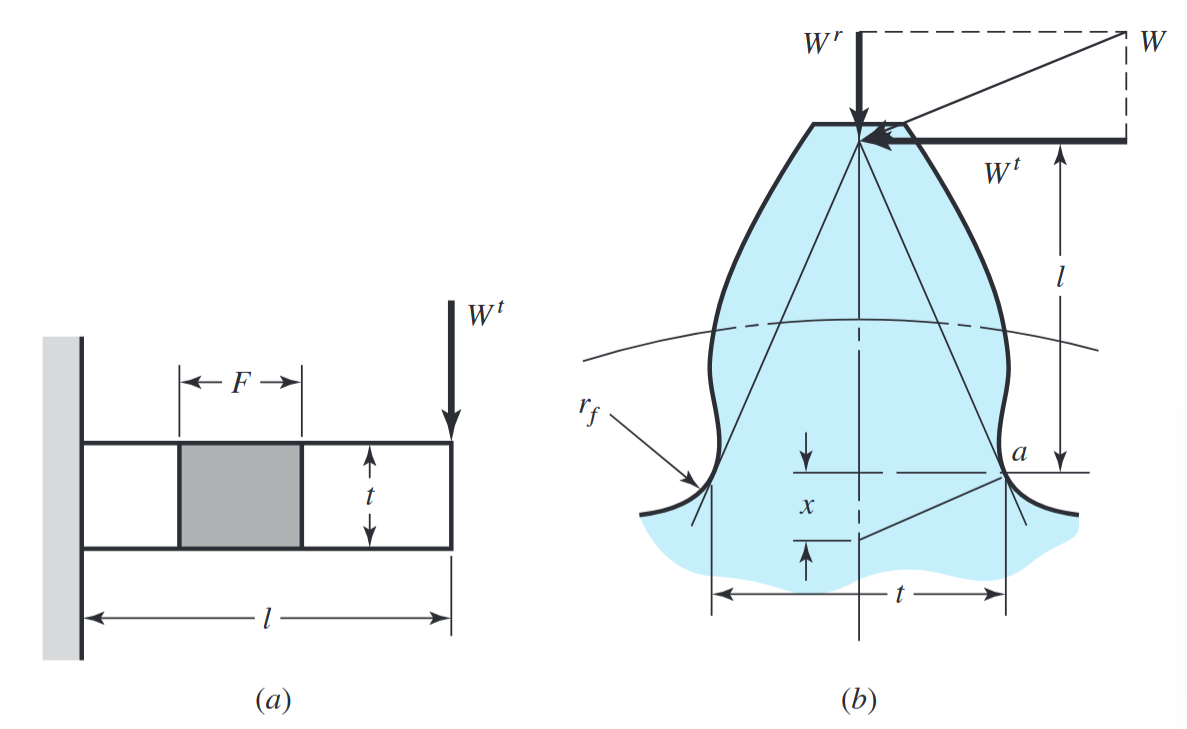
bookhue

פרופיל השן, מצויר בצורה מוזרה. ב-(a) מוצגת השן וגם עובי השן , וצורת סימון זו די נפוצה אז כדאי להכיר. בקורס אנו מסמנים במקום . (Budynas et al., 2015).

עם עוד פיתוחים בדרך אנו מגיעים למסקנה ש:

כאשר:

ונזכור ש- הוא הפסיעה הקטרית, המקיים .

ל- אנו קוראים מקדם הצורה של השן, וניתן למצוא ערכים שלו בטבלה 14-2. נשים לב שככל שמספר השיניים גדל ערכי גדלים, ולכן מאמץ הכפיפה קטן!

השפעות דינמיות

כאשר זוג שיניים נע בקצב מהירות יחסית די גבוה, נוצר רעש, וחלים השפעות דינמיות על השיניים. כדי להתייחס להשפעות דינמיות אלו, ביצעו ניסויים על מספר גלגלי שיניים במהירות , ובמהירות כלשהי. אם למשל במהירות אפסית הגלגל שיניים נכשל בעומס משיקי , ובמהירות משיקית הוא נכשל ב-, אז המקדם הדינמי מוגדר כ- עבור מהירות .

הערה:

ההגדרה של המקדם הדינמי השתנתה בעבר. סטנדרט ANSI/AGMA 2001-D04 מכיל את האזהרה הבאה:
bookhue

פותחו ביטויים ל- כתלות בפרופיל ובאופן בו השן נוצרה. אם המהירות המשיקית היא:

כאשר:

  • המהירות המשיקית ב-.
  • הקוטר הוא ב-.
  • המהירות הזוויתית היא ב-.

אז לפי AGMA:

אם נרצה להתייחס למקדם הדינמי בנוסחת לואיס:

הערה:

בגג”ש ישרות, הרוחב של השן (b) בדרך כלל גדול מהפסיעה פי .

גם עם התיקון הדינאמי, יש בפיתוח לואיס מספר הנחות שגויות:

  • רק מאמץ הכפיפה נלקח בחשבון.
  • הכוח מופעל בקצה השן (אבל תאכלס הוא מופעל במיקום יותר נמוך).
  • רק שן אחת נמצאת במגע.

לכן, פותחו המון נוסחאות שונות לחישוב המאמצים בשן, שבחלק מן ההנחות יותר מחמירות וחלק יותר מחמירות מאשר לואיס. אנחנו בקורס נעבוד עם משוואות AGMA.

משוואות מאמץ AGMA

ישנם שתי משוואות בסיסיות לחישוב המאמצים בשן גג”ש - אחת למאמץ הכפיפה, והשנייה למאמץ מגע.

משוואת AGMA למאמץ כפיפה

עבור מאמץ כפיפה, AGMA מציעים את הנוסחה הבאה:

כאשר:

  • המאמץ הוא מאמץ הכפיפה ב-. נקרא גם bending stress number.
  • העומס הוא העומס המשיקי ב-.
  • האורך הוא רוחב השן ב-.
  • האורך הוא המודול החזיתי ב-. במקרה של גג”ש ישרות הוא פשוט .
  • המקדם הוא מקדם עומס יתר.
  • המקדם הוא מקדם הגודל.
  • המקדם הוא מקדם התפלגות העומס (מסומן גם ).
  • המקדם הוא מקדם עובי הזר.
  • המקדם הוא מקדם הצורה לחוזק כפיפה, והוא כולל גם את מקדם ריכוז המאמצים , ואת התיקון לעומס שלא פועל בקצה השן.

יותר נוח לפעמים להציב את הנוסחה:

מקדם עומס יתר

התפקיד של מקדם העומס יתר הוא להתייחס להחרגות צפויות מעבר ל-, על בסיס ניסיון. דוגמה לטבלה של עבור סוגים שונים של מכונות:
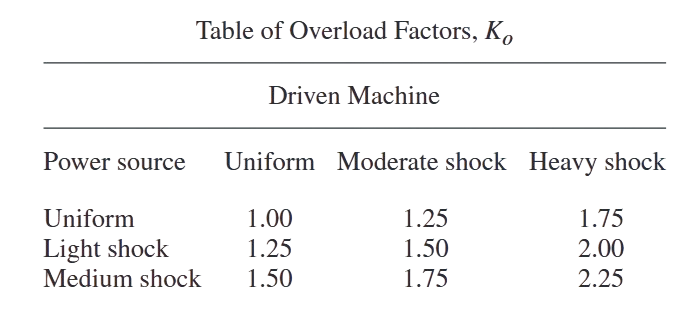
bookhue

דוגמה לטבלת מקדמי עומס יתר. (Budynas et al., 2015).

הערה:

עבור , שיטת AGMA מאפשרת יכולת נשיאת עומס יתר רגעי של .

מקדם דינאמי

כפי שהוסבר מקודם, המקדם הדינאמי לוקח בחשבון סטיות בייצור השיניים (transmission errors). מספר הגורמים לשגיאות אלו הם:

  • רעידת השיניים במהלך השילוב כתוצאה מקשיחות השיניים.
  • המהירות הקווית.
  • דפורמציה של השיניים.

כדי להתייחס להשפעות אלו AGMA הגדירו מספר מקדמי איכות . מספרים אלו מגדירים את הטולרנסים של גירים שונים. מקדמי איכות בטווח ל- כוללים את רוב התמסורות המסחריות. הטווח עד הינו עבור גלגלי שיניים באיכות ודיוק גבוהים.

המשוואות הבאות מבוססות על מקדמי איכות אלו:

כאשר:

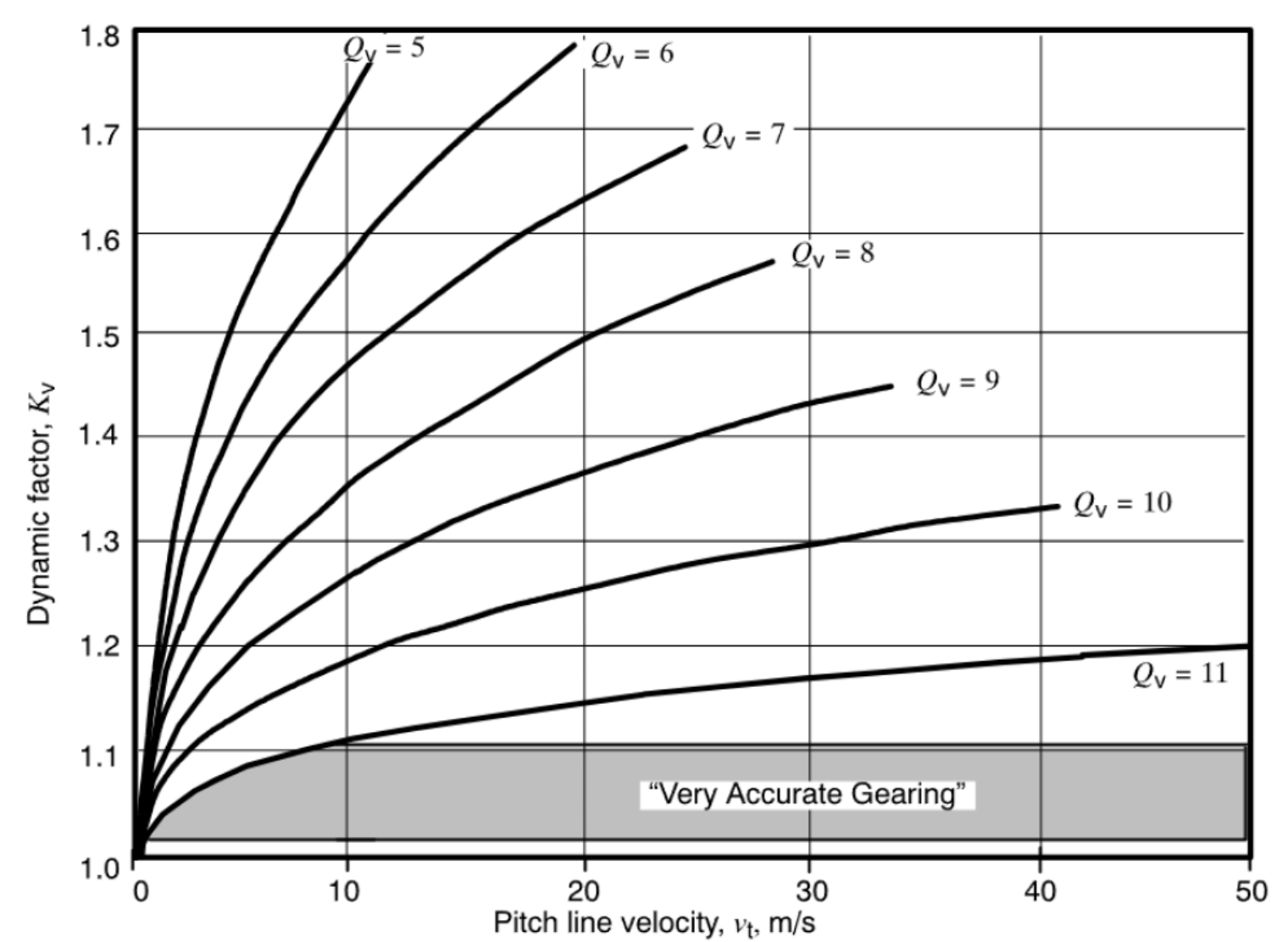
bookhue

מקדם דינאמי . המשוואות לעקומים אלו נתונים במשוואות (SH14-27), ונקודות הסוף ב-(SH14-29). (ANSI/AGMA 2001-D04).

הגרף לעיל מתאר את משוואה (SH14-27). המהירות המקסימלית לכל מקדם איכות הוא הקצה של כל עקומת , והיא נתונה ע”י:

מקדם הגודל

מקדם זה מבטא חוסר אחידות בתכונות חומר הגלם, ומושפע מ:

  • גודל השן
  • קוטר הגלגל
  • יחס גודל השן לממדי הגלגל.
  • רוחב הגלגל.
  • הטיפול התרמי.
    מלקיחת כל השפעות אלו בחשבון אנו מניחים כי: כאשר הוא מקדם תיקון לגודל.
    כאשר קטן מ- נשתמש ב- .

בקורס שלנו מוצע ביטוי מופשט:

מקדם התפלגות העומס

מקדם התפלגות העומס מבטא חוסר אחידות פילוג העומס על פני קו הפעולה, ומושפע מ:

  • סטיות ייצור.
  • סטיות הרכבה - קוויות הגלים.
  • מעוות כתוצאה מהעומס.
  • מעוות כתוצאה מאפקטים תרמיים וצנטריפוגליים.

הוא מוגדר כעומס המרבי (peak) מחולק לעומס הממוצע לרוחב השן.

כאשר הוא מקדם תיקון צורה:

הוא נובע מהכתרה (crowning), שהוא טיפול המבצעים לשן כדי ליצור מגע מקומי במרכז השן או כדי למנוע מגע בקצותיהן. זהו תהליך יקר, אבל הוא מפחית את הרעש ומאריך את חיי השיניים. עם זאת, ביצוע הכתרה גדולה מהנדרש, אזור מגע השן הופך קטן מדי, מה שעלול להשפיע לרעה על חוזק השן.

הכתרה על גלגל שיניים.

מקדם יחס הפיניון ותיקונו מתחשבים במעוות הפיניון כתוצאה מהעומס.

עבור נשתמש ב- .
התיקון למקדם יחס הפיניון לוקח בחשבון את מיקום הפיניון ביחס למסבים התומכים.

כאשר ו- מוגדרים כפי שמוצג באיור הבא:
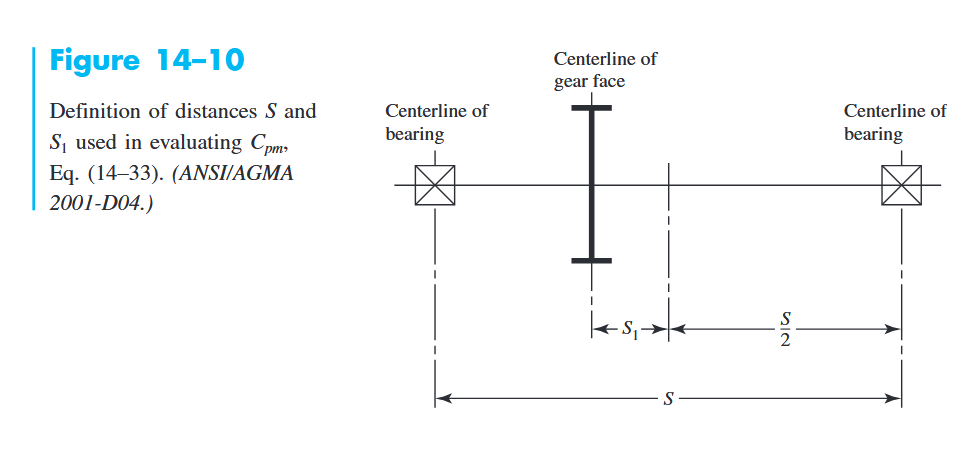
bookhue

הגדרות המרחקים ו-. (Budynas et al., 2015).

מקדם קוויות השילוב ותיקונו מתחשבים בחוסר הקוויות שבין ציר הסיבוב כתוצאה מכלל הסיבות, מלבת מעוות אלסטי (casing).

כאשר הערכים של נמצאים בטבלה 14-9, או מהגרף:
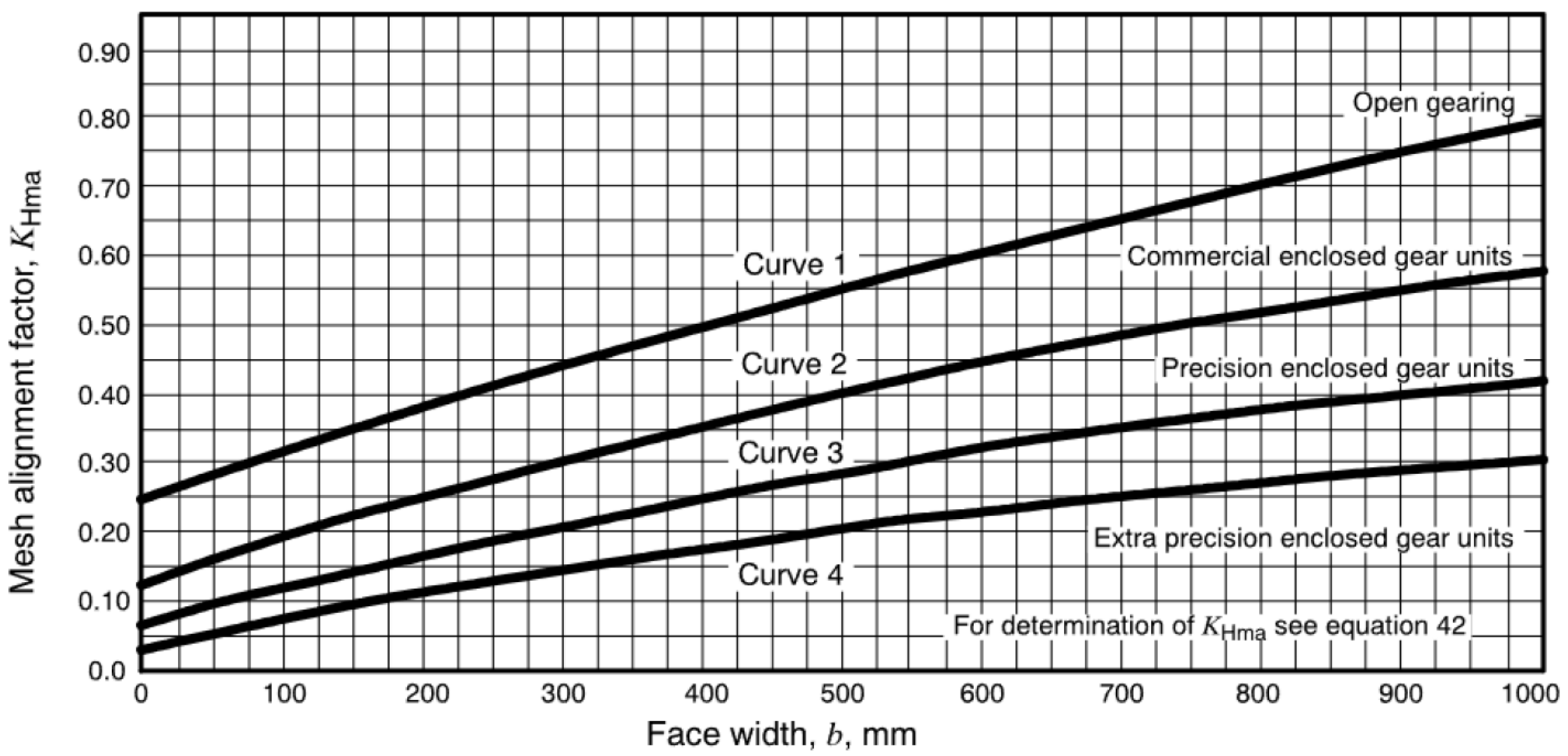
bookhue

מקדם קוויות השילוב , לאחר curve-fitting מטבלה 14-9. (ANSI/AGMA 2001-D04).

התיקון שמציעים עבורו:

מקדם הצורה

מקדם הצורה דומה עקרונית למקדם הצורה של לואיס. הוא משתנה כתלות במספר השיניים בפיניון ובגיר,. הוא כולל את השפעתם של שלושת הגורמים הבאים:

  • ריכוז מאמצים להתעייפות .
  • חלוקת העומס בין השיניים .
  • נקודת הפעלת העומס על השן.

המשוואה שמקבלים למקדם הצורה עבור גג”שים ישרות ומשופעות היא:

כאשר:

  • ניקח לגלגלי שיניים ישרים ו- לגלגלי שיניים משופעות.
  • הגודל הוא לא מקדם צורה של לואיס בכלל. הוא ערך שנלקח מ- AGMA 908 B-89.
  • המקדם הוא מקדם המאמצים להתעייפות.

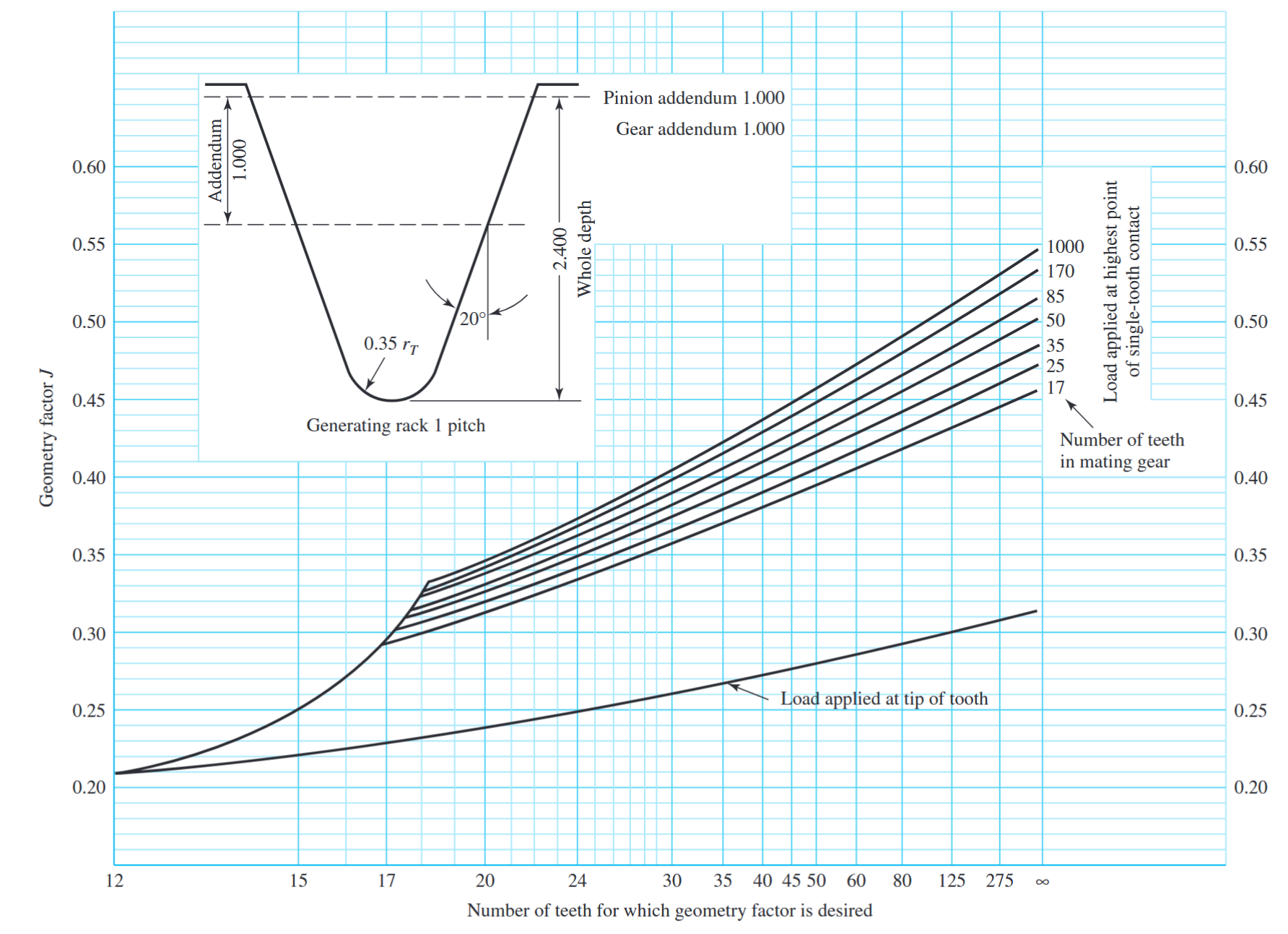
bookhue

מקדמי צורה () לשיניים ישרות. נלקח מ- AGMA 218.01, שהוא עקבי עם ערכים מטבלה ב- AGMA 908-B89.

מקדם עובי הזר

אם עובי השפה אינו מספיק כדי לספק תמיכה מלאה לשורש השן, כשל להתעייפות בכפיפה יכול להתרחש באזור עובי השפה ולא באזור הפילט (fillet).
נגדיר:

כאשר הוא גובה השן.
עבור גג”ש מלא, אנו יודעים לחשב את רדיוס המעגל העיקרי באופן הבא:

מקדם עובי הזר מחושב באופן הבא:

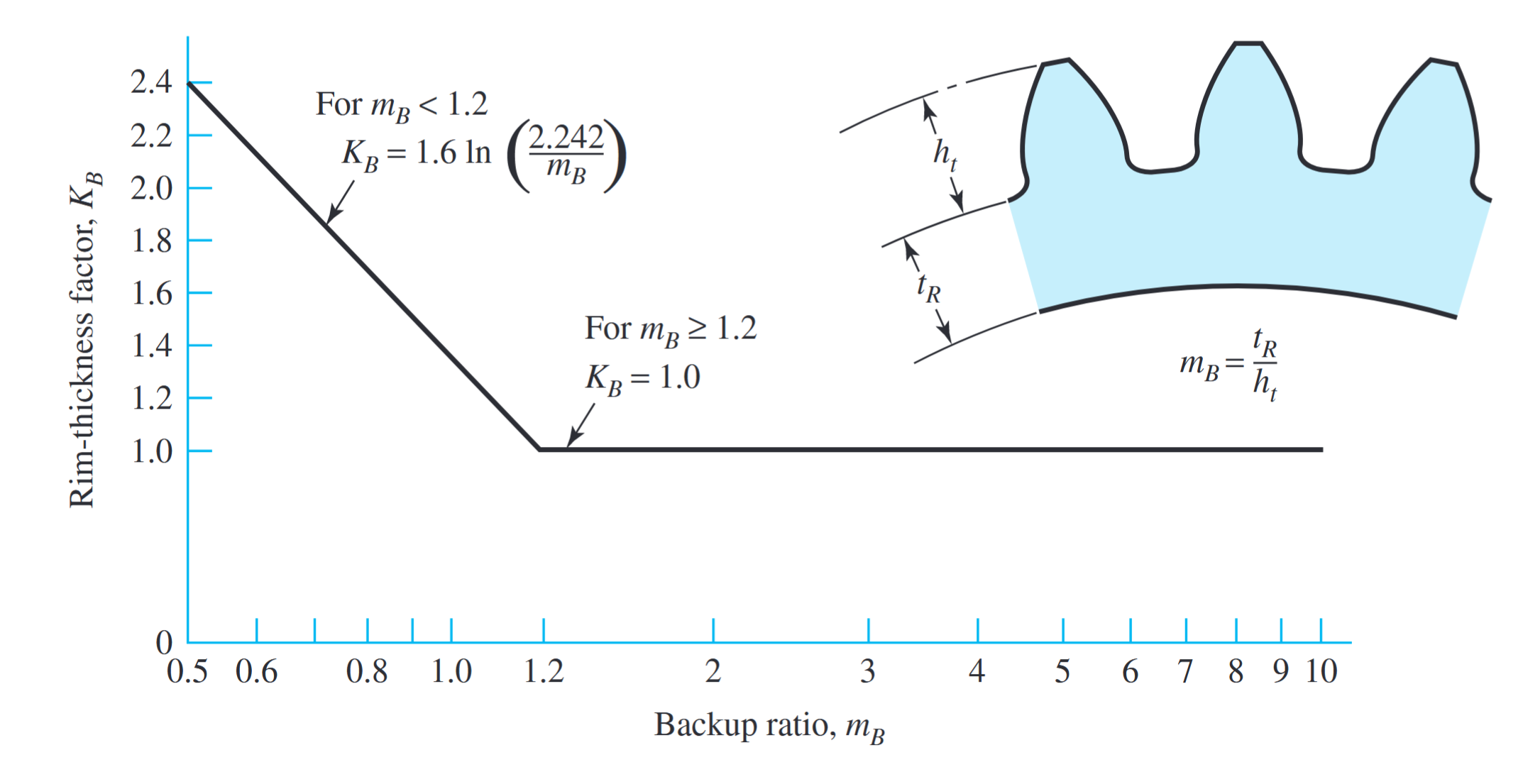
bookhue

מקדם עובי הזר . (ANSI/AGMA 2001-D04).

מאמץ כפיפה מותר

המשוואה למאמץ כפיפה מותר היא:

כאשר:

הערה:

עבור מאמצי כפיפה מתחלפים (שהסימן שלהם מתחלף במהלך מחזור אחד, למשל אם הם תונדים סביב האפס, שזה קיים בבטלנים) מומלץ להכפיל את ב-.

אם מבקשים למשל למצוא רוחב שן מינימלי, אז נדרוש , ואז נוח להציב בנוסחה:

או אם למשל רוצים הספק מינימלי:

חוזק לכפיפה

החוזק לכפיפה תלוי בסוג החומר של גלגל השיניים, ובטיפולים התרמיים שהוא עבר.
החומר הנפוץ ביותר לייצור גלגלי שיניים בתעשיית המכונות הינו פלדה מסוגסגת, ופלדה פחמנית המכילה . לשימושים מסוימים נעשה שימוש גם במתכות צהובות ובחומרים פלסטיים. הפלדה לייצור גלגלי שיניים הנה בתצורת חומר גלם מחושל או יצוק או מוטות מעורגלים. הגג”שים העשויים פלדה עוברים טיפול תרמי, בכפוף לאפליקציה ולסוג הפלדה.

כדי לקבוע את החוזק לכפיפה אנו ניעזר בטבלאות וגרפים:

הערה:

ב-AGMA הסימון לחוזק הכניעה הוא במקום .

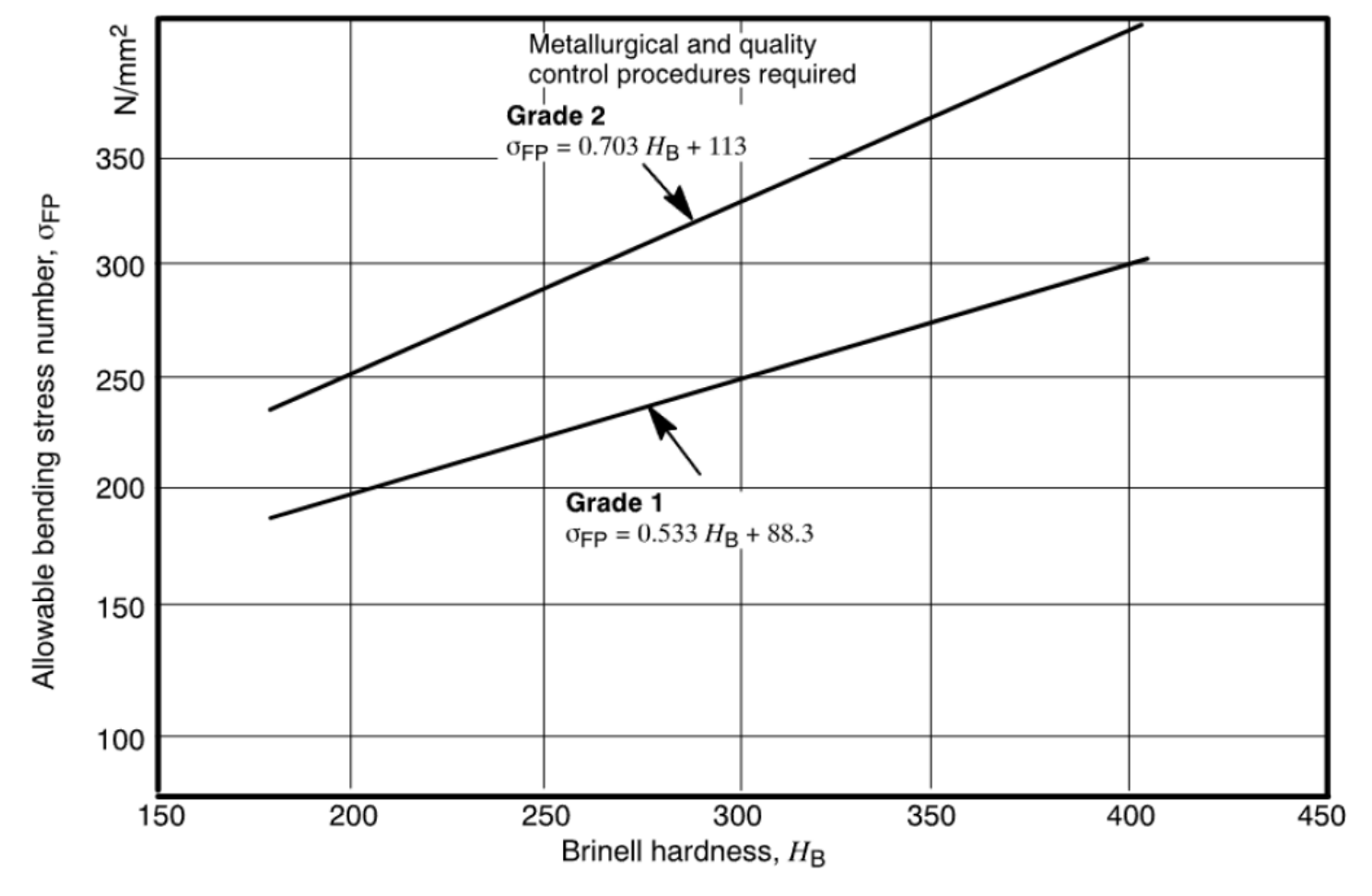
bookhue

חוזק לכפיפה של פלדה שעברה חיסום מלא, בעמיסה חד כיוונית, מיליון מחזורי עמיסה, ו- אמינות. (ANSI/AGMA 2001-D04).

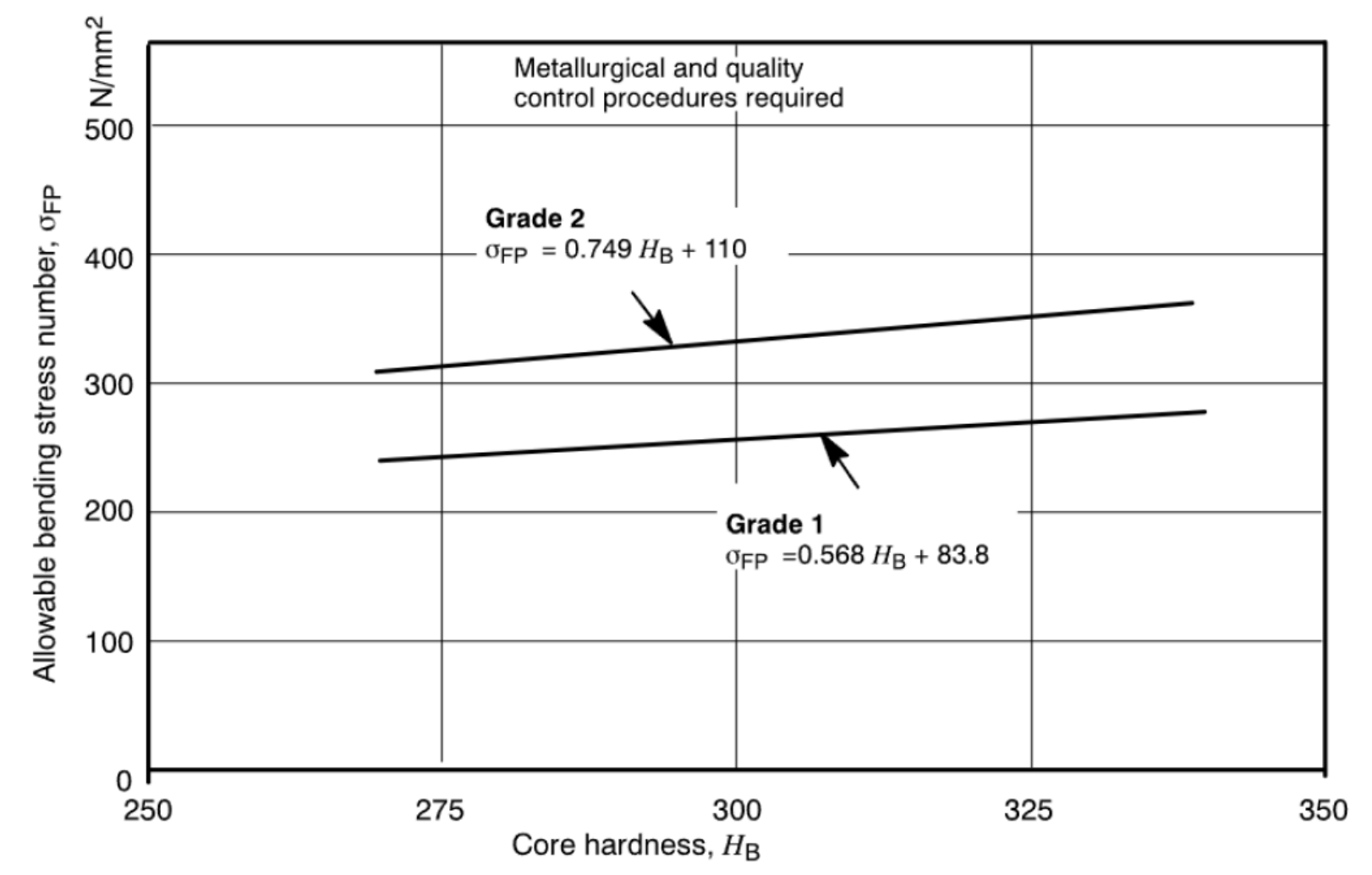
bookhue

חוזק לכפיפה לפלדה שעברה חנקון מלא (למשל AISI 4140, AISI 4340), בעמיסה חד כיוונית, מיליון מחזורי עמיסה, ו- אמינות. (ANSI/AGMA 2001-D04).

הגודל נקרא קשיות ברינל (Brinell Hardness), והוא אחד מהמאפיינים של חומר הגג”ש הוא מגיע ביחידות של , או, כמו שמוצג ב-AGMA, יחידות (זהה ל-).

מקדם מספר מחזורים לכפיפה

מאחר והבדיקות נעשו עבור מחזורים, אם אורך החיים הנדרש קצר או ארוך יותר, נצטרך להתאים את החוזק לכפיפה בהתעייפות בהתאם לעקום של החומר.

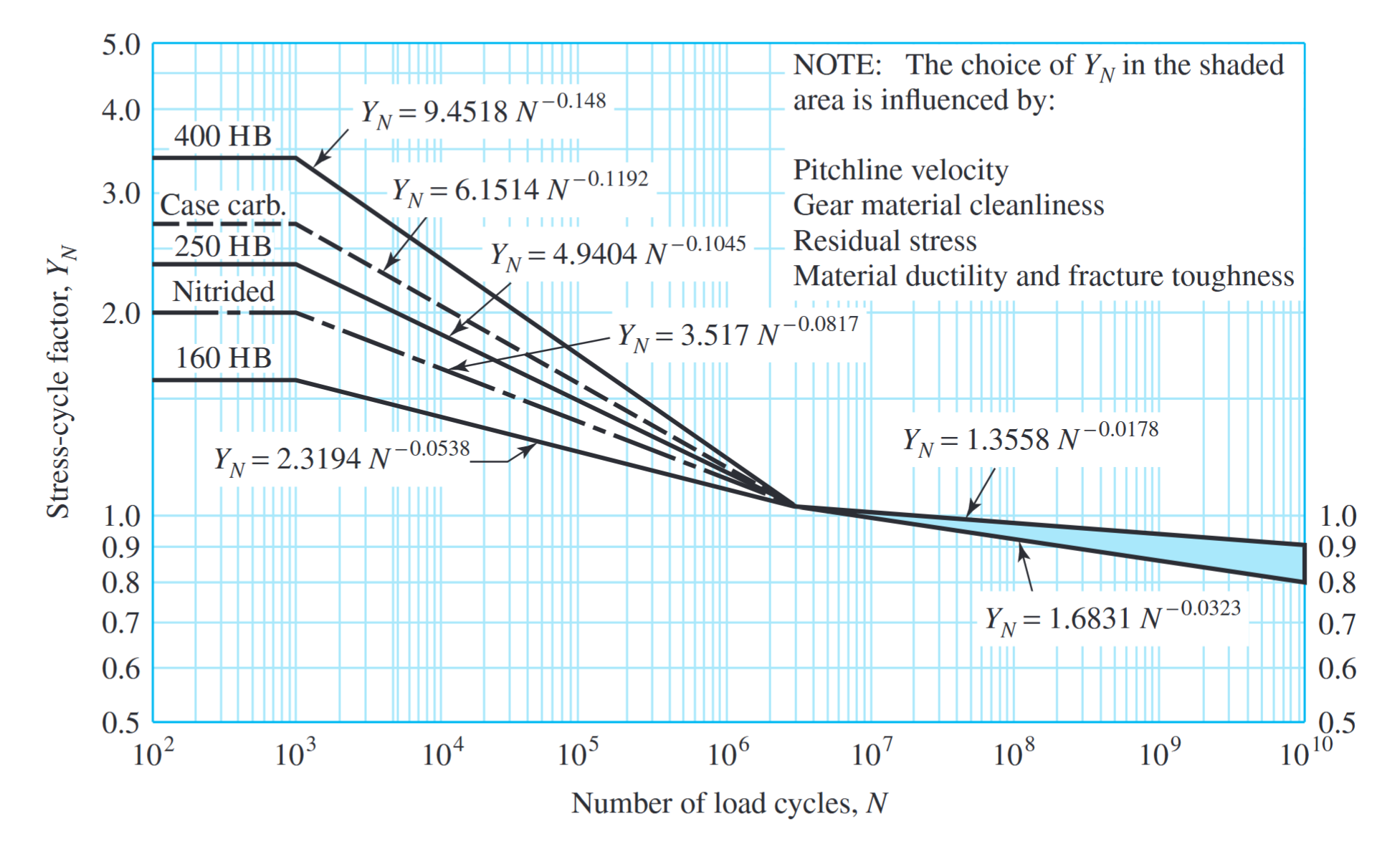
bookhue

מקדם מספר מחזורים לכפיפה . (ANSI/AGMA 2001-D04).

הערה:

מעל מחזורים, נשתמש בעקומה העליונה לתנאים רגילים, ואם מבקשים מאיתנו מצב קריטי עלינו לבחור את העקומה התחתונה.

אם נותנים לנו את אורך החיים בשעות נחשב את מספר המחזורים הנדרש באופן הבא:

כאשר הוא אורך החיים בשעות, היא המהירות ב-, ו- הוא מספר המגעים בסיבוב.
מבחינת , מספר המגעים בסיבוב, אם למשל הגג”ש אותו אנו בודקים בא במגע עם שני גלגלי שיניים, אז , כי כל שן אצלו נמצאת במגע פעמיים בסיבוב אחד שלו, מה שמכפיל את מספר המחזורים שהוא עובר בכפיפה.

מקדם טמפרטורה

מקדם הטמפרטורה לוקח בחשבון את טמפרטורת הגג”ש. טמפרטורת שמן הסיכה מהווה מדד לטמפרטורת גלגל השיניים. עבור גלגלי השיניים עשויים פלדה ניתן להשתמש ב- עבור .

הערה:

בקורס שלנו נשתמש במקדם שווה ל- גם בתרחיש חם וקר כל עוד לא הוגדר אחרת.

מקדם אמינות

מקדם האמינות לוקח בחשבון את הפילוג הסטטיסטי הנורמאלי הקיים לגבי נתון החוזק של חומר הגלם. הוא נתון ע”י:

או פשוט נשתמש בטבלה 14-10.

מקדם הביטחון למאמצי כפיפה

סטנדרט ANSI/AGMA 2001-D04 מיכל מקדמי ביטחון נגד התעייפות בכפיפה . הגדרתו:

במקרה זה מקדם הביטחון לינארי עם המאמץ.

משוואת AGMA למאמצי מגע

כאשר שני גופים עם משטחים עקומים נלחצים אחד על השני בעומס , מגע נקודתי או קווי הופך למגע משטחי למאמצים המתפתחים בעומסים אלו אנו קורים מאמצי מגע (contact stresses). אנו נניח שבגלגלי שיניים המגע בקירוב מתרחש כמו מגע בין שני גלילים.

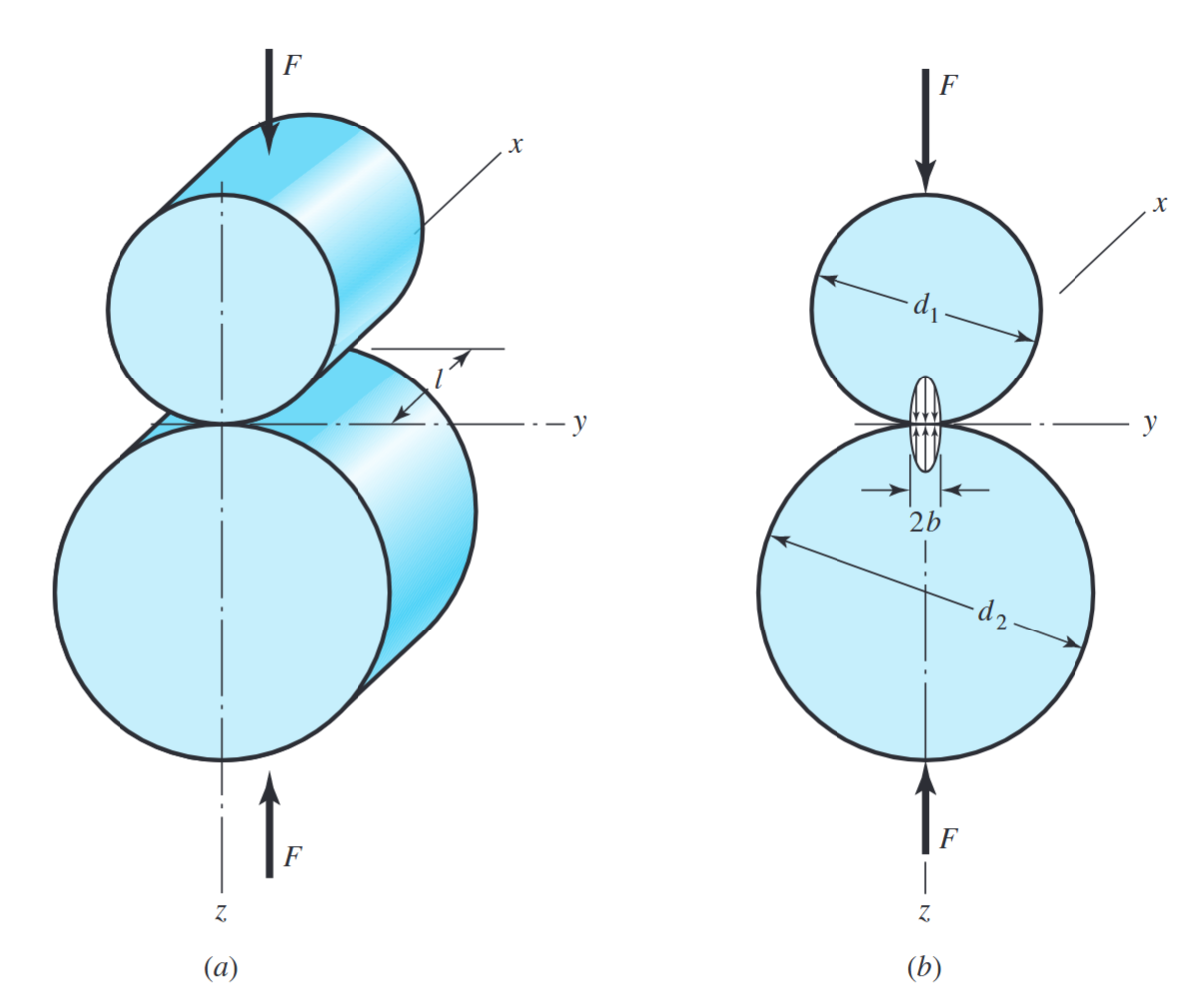
bookhue

מאמץ מגע בין שני גלילים. (Budynas et al., 2015).

נוסחת AGMA למאמץ מגע היא:

כאשר:

מקדם גאומטרי לחוזק מגע

מקדם גאומטרי לחוזק מגע הוא מקדם הלוקח בחשבון את זווית הלחץ בין הגירים באופן הבא:

כאשר, כמו מקודם, לגלגלי שיניים ישרות, ו- לגלגלי שיניים משופעות.

מקדם אלסטיות

מקדם האלסטיות לוקח בחשבון את תכונות החומר האלסטיות. ערכו מחושב ע”פ:

או שפשוט נשתמש בטבלה 14-8.

מקדם עיבוד פני השטח

מקדם עיבור פני השטח מושפע מפני השטח כתוצאה משיטת העיבוד (שיבוב, ליטוש, השחזה, shot peeing וכו’). AGMA טרם קבוע ערכים למקדם זה אך מוצע כי ערכו יהיה גדול מ- כאשר מזוהים פגמים על פני השטח. בקורס שלנו נניח .

מאמץ מגע מותר

מאמץ המגע המותר , באופן דומה למאמץ כפיפה מותר, הוא:

כאשר:

חוזק למגע

כמו חוזק לכפיפה, את החוזק למגע נוכל להוציא מטבלאות וגרפים, כמו הגרף הבא:
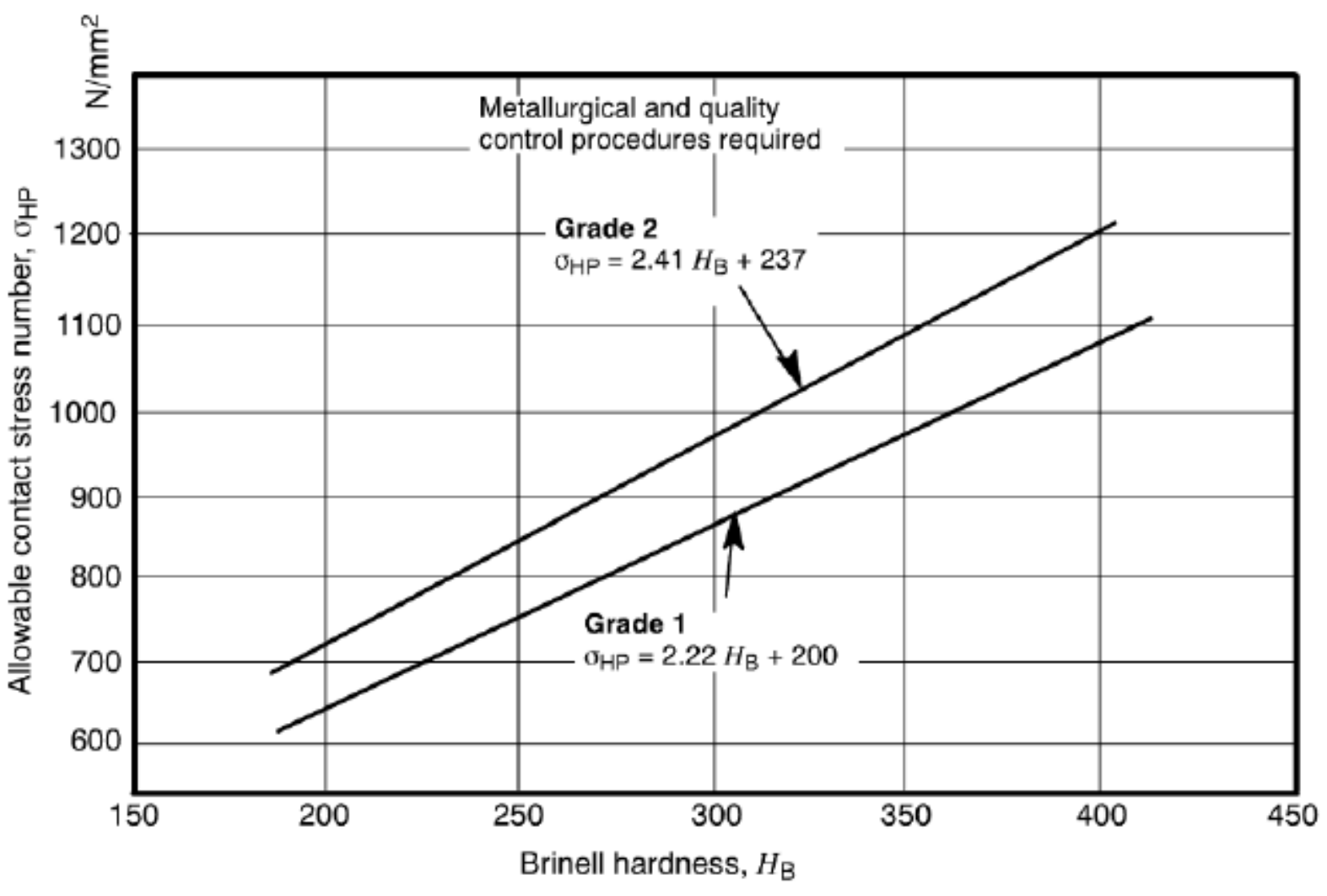
bookhue

חוזק למגע של פלדה שעברה חיסום מלא, בעמיסה חד כיוונית, מיליון מחזורי עמיסה, ו- אמינות. (ANSI/AGMA 2001-D04).

מקדם מספר מחזורים למגע

כמו מקדם מספר מחזורים לכפיפה, מקדם מספר מחזורים למגע מתקן את המאמץ מגע לאורך חיים הנדרש, במקום אורך החיים עליו התבצעו הבדיקות, . כדי לחשב את ה- הדרוש, נוכל עדיין להשתמש בנוסחה ממקודם.
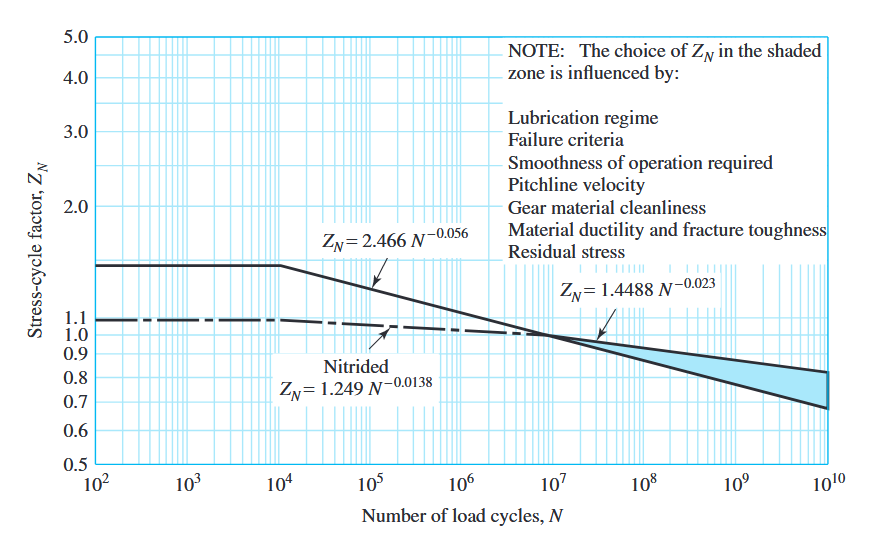
bookhue

מקדם מספר מחזורים למגע . (ANSI/AGMA 2001-D04).

הערה:

מעל מחזורים, נשתמש בעקומה העליונה לתנאים רגילים, ואם מבקשים מאיתנו תנאי קריטי עלינו לבחור את העקומה התחתונה.

מקדם יחס קושי

לפיניון לרוב מספר שיניים קטן מאשר לגיר ולכן סובל ממספר רב יותר של מחזורי מגע. ניתן להגיע לחוזק פני שטח אחיד ע”י ייצור פיניון קשה יותר מאשר הגיר. מקדם יחס הקושי משמש רק את הגיר, כך שעבור פיניון .

עבור פלדה בחיסום מלא:

כאשר:

כאשר הוא הקשיות של הפיניון ו- הוא הקשיות של הגיר.

מקדם ביטחון למאמצי מגע

מקדם הביטחון למאמצי מגע מוגדר כ:

במקרה זה מקדם הביטחון לינארי עם המאמץ. את מקדם הביטחון נבחר להיות אלא אם כן צוין אחרת או שיש גורם אי וודאות.

גאומטרייה של גלגל שיניים משופעות

באיור הבא מתוארים גלגלי שיניים משופעות, המעבירות תנועה בין גלים מקבילים:
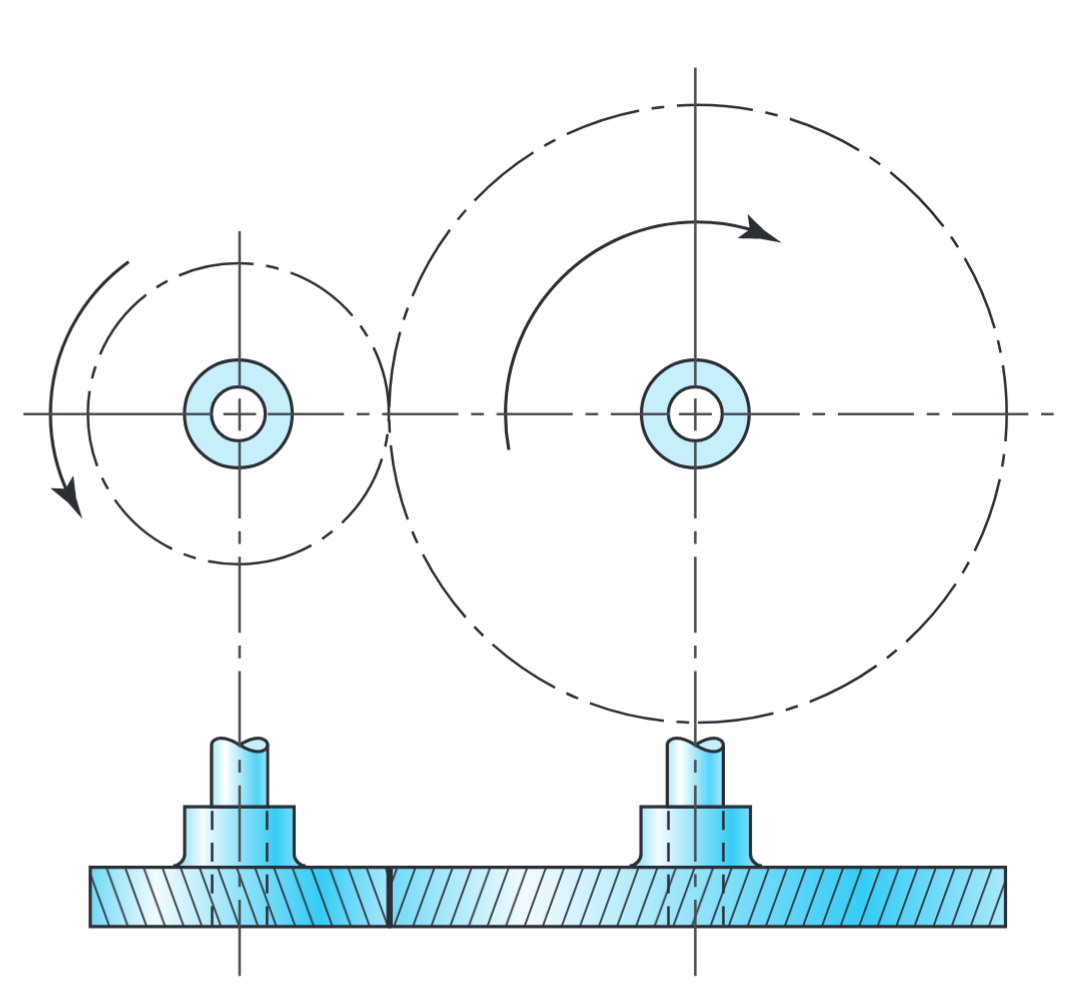
bookhue

תמסורת משופעת להעברת תנועה בין גלים מקבילים (וגם לא מקבילים). (Budynas et al., 2015).

זווית השיפוע זהה על כל גג”ש, אבל לגג”ש אחד יש שיפוע ימני ולשני יש שיפוע שמאלי. הצורה של השן היא פשוט אבולונט המוארך בזווית:
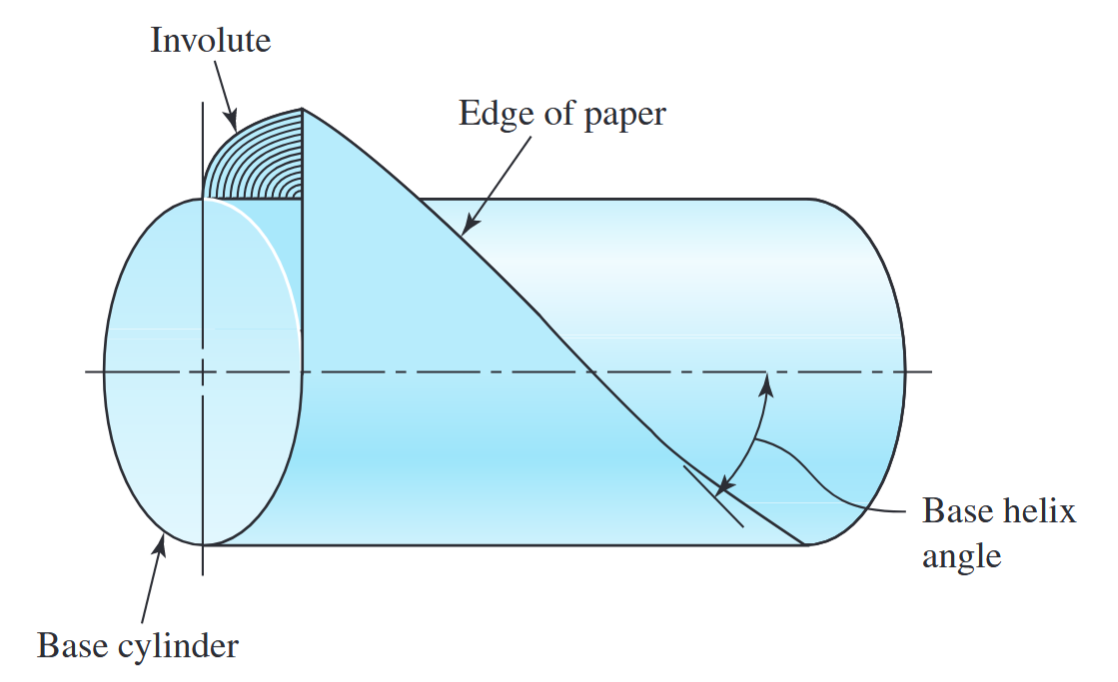
bookhue

נביט בגאומטרייה של גג”ש משופע על פס שיניים:
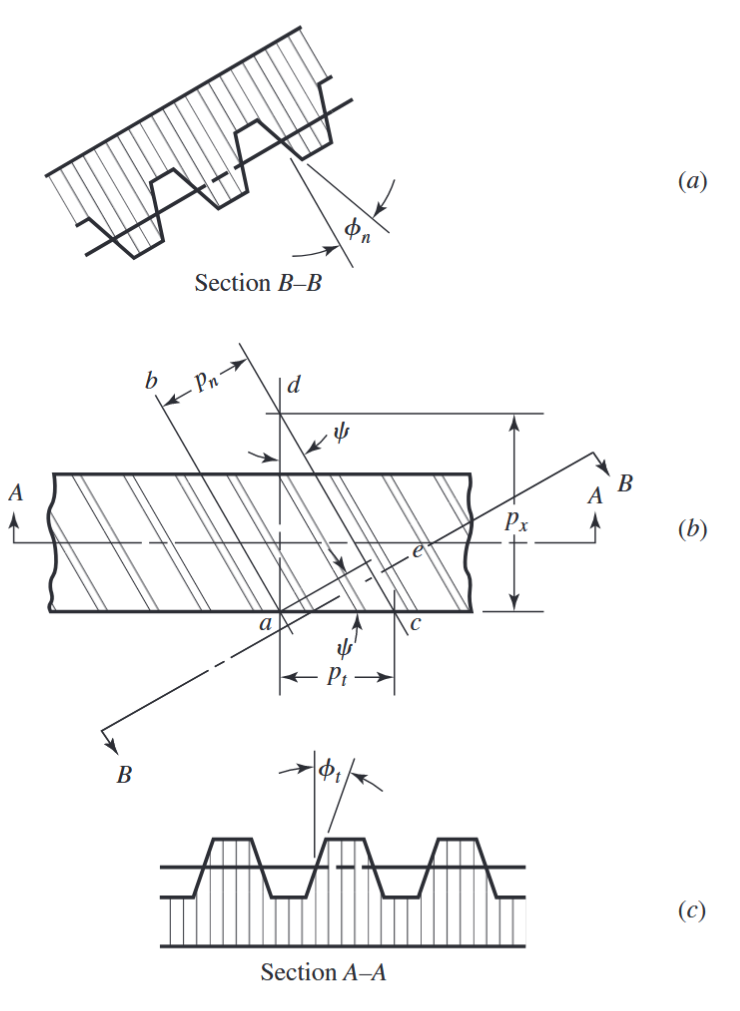
bookhue

מונחים וסימונים בגג”ש משופע. (a) הטלה על המישור הנורמלי. (b) מבט על. (c) הטלה על המישור החזיתי.

הערה:

קוראים למישור החזיתי גם המישור המשיקי, ובהתאמה לכך גם כל הרכיבים המתאימים. אז למשל נקרא המודול החזיתי/משיקי.

האיור לעיל מציג את המבט על, על פס שיניים משופע. הקווים ו- הם הקווי אמצע של שתי שיניים צמודות באותו מישור הפסיעה. הזווית היא זווית השיפוע. המרחק הוא הפסיעה ההיקפית האורכית/חזיתית במישור הסיבוב (הפסיעה ההיקפית במקרה של גג”ש ישרות). המרחק הוא הפסיעה הנורמלית ההיקפית והיא קשורה לפסיעה ההיקפית בצורה הבאה:

המרחק נקרא הפסיעה הצירית , והוא נתון ע”י:

מאחר ו- , הפסיעה ההיקפית הקוטרית היא:

זווית הלחץ בכיוון הנורמלי שונה מזווית הלחץ בכיוון הסיבוב (המשיקי), בגלל הטיית השיניים. זוויות אלו תלויות אחת בשנייה ע”י:

המודול יהיה המודול החזיתי - המודול ממבט החזית, שהוא:

קוטר המעגל הראשי (האדנדום) והמעגל העיקרי (הדידנדום):

קוטר החלוקה/פסיעה הוא קוטר החלוקה/פסיעה החזיתי:

המרחק בין המרכזים של שני גג”שים:

הערה:

שימו לב שאת תפקיד המודול בגלגלי שיניים ישרות לוקח המודול המשיקי (חזיתי) . אבל, כאשר נתון לנו מודול כלשהו , או זווית לחץ כלשהי , הכוונה למודול/זווית הלחץ הנורמלית:

ניתוח כוחות - גג”ש משופעות

באיור הבא מתואר מבט תלת ממדי על של הכוחות הפועלים על שן משופעת:
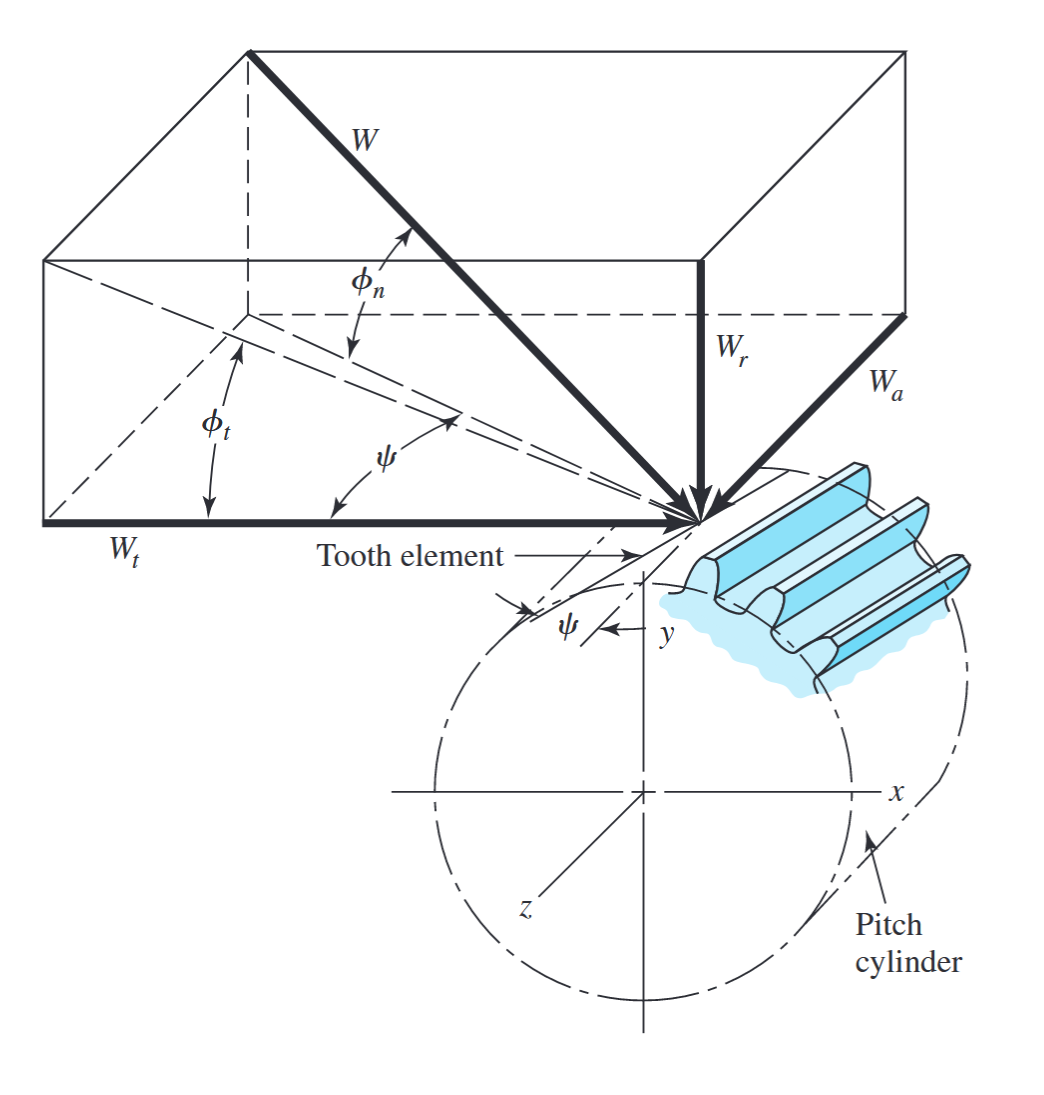
bookhue

כוחות הפועלים על שן משופעת ימנית.

נקודת הפעלת הכוחות נמצאת על מישור הפסיעה, ובמרכז פני הגג”ש. מהגאומטרייה של האיור, שלושת הרכיבים של סך הכוח על השן הם:

כאשר:

  • הכוח הוא סך הכוח.
  • הכוח הוא הרכיב הרדיאלי.
  • הכוח הוא הרכיב המשיקי.
  • הכוח הוא הרכיב הצירי.

לרוב, אנו יודעים את ואנו רוצים למצוא את הכוחות האחרים, אז נעשה פשוט הצבות כדי לקבל:

הערה:

בממסרת רב-דרגתית יש לשים לב כי הכוח הצירי הפועל על הגג”ש מושפע גם מהכוח הצירי בגג”שים האחרים:

משוואות מאמץ לגג”ש משופעות

משוואות המאמץ, בין אם כפיפה ובין אם מגע, לשיניים משופעות, זהות למשוואות AGMA לשיניים ישרות:

ישנם הבדלים במקדם הגאומטרי לחוזק כפיפה ומקדם גאומטרי לחוזק מגע .

מקדם צורה לגג”ש משופעות

כמו במקדם צורה לגג”ש ישרות, את מקדם הצורה אנו יכולים לקחת מטבלה/גרף.
לגג”ש משופעות חישבו את מקדמי הצורה לגג”שים עם שיניים, וכדי להכליל למספרי שיניים שונים, אנו מבצעים תיקון עם .

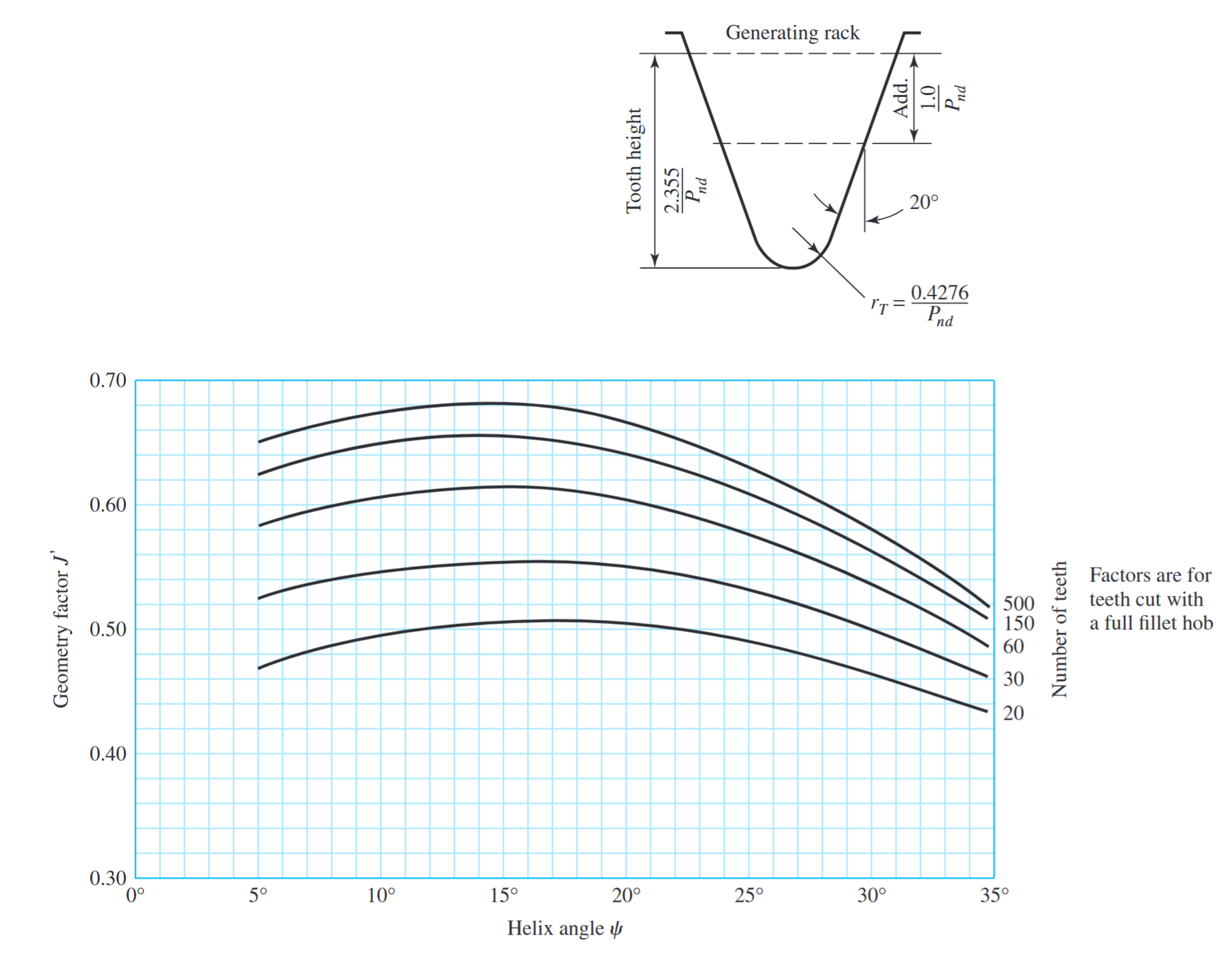
bookhue

מקדמי צורה לגג”ש משופעות , עם שיניים. נלקח מ- AGMA 218.01, שהוא עקבי עם ערכים מטבלה ב- AGMA 908-B89.

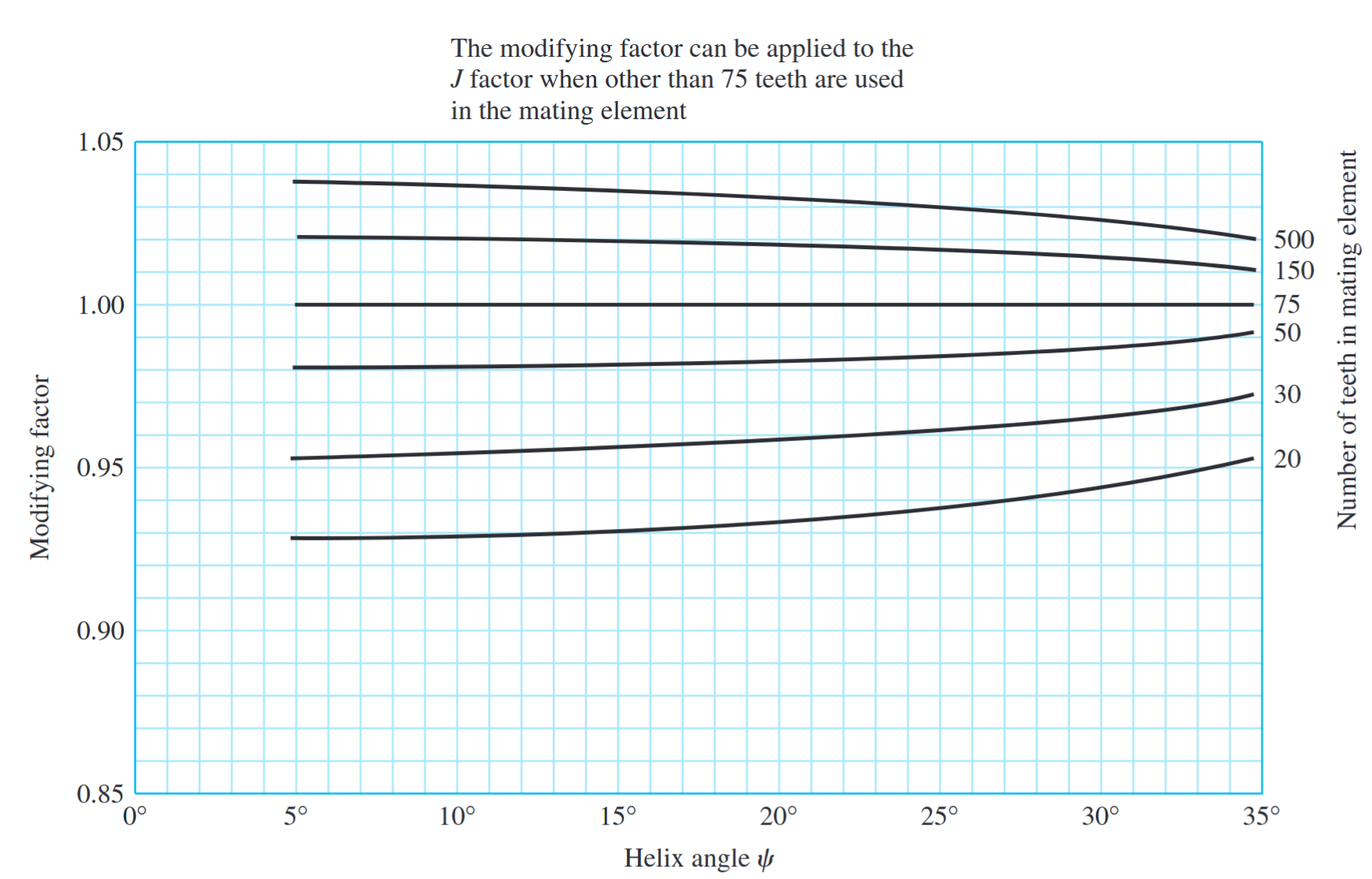
bookhue

מקדם תיקון למקדם צורה לשימוש על גג”ש משופעות שיש להם מספר שיניים שונה מ-. נלקח מ- AGMA 218.01, שהוא עקבי עם ערכים מטבלה ב- AGMA 908-B89.

כעת, כדי לחשב את :

מקדם גאומטרי לחוזק מגע לגג”ש משופעות

כמו במקדם גאומטרי לחוזק מגע לגג”ש ישרות, את לגג”ש משופעות אנו מחשבים לפי:

בגג”ש ישרות, אמרנו ש- . עבור משופעות, אנו מחשבים את יחס חלוקת העומס באופן הבא:

כאשר הוא פסיעת הבסיס במישור הנורמלי, שבגג”ש ישרות:

הגודל הוא אורך קו הלחץ במישור החזיתי, והוא מחושב ע”י:

כאשר ו- הם רדיוסי הפסיעה ו- ו- הם רדיוס הבסיס של הפיניון והגיר בהתאמה. נזכור כי ניתן לחשב את רדיוס הבסיס ע”י:

בנוסף, הוא גובה ראש השן, שהוא פשוט .

הערה:

כאשר משתמשים במשוואה (SH14-25), כיוון שיש שימוש משולב במודול הנורמלי ובמודול המשיקי, ייתכן כי אחד מהביטויים בסוגריים המרובעות גדולות יותר מהביטוי השלישי. במקרה זה אנו צריכים להחליף את ביטוי זה בביטוי השלישי.

תרגילים

תרגיל 1

נתונה מערכת של שלושה גג”שים כמתואר באיור.

סכמת הבעיה.

מספר השיניים:

זוויות הלחץ הן:

המודול הוא ומועבר הספק של לתמסורת בגג”ש אשר מסתובב במהירות סיבוב ויוצא מהתמסורת לסיבוב מדחף המחובר לציר של גג”ש .

סעיף א’

חשב את מהירויות הסיבוב של גג”ש ושל גג”ש .

פתרון:
היחס תמסורת לפי מספר גלגלי השיניים:

לאחר העברת אגפים נקבל:

באופן דומה נקבל את המהירות הזוויתית של גיר :

נשים לב שמהירות הסיבוב של גג”ש אינה תלויה במספר השיניים של גג”ש ולכן גג”ש משמש כבטלן.

סעיף ב’

חשב את רכיבי הכוחות המשיקים בין גג”ש ל- ובין גג”ש ל-.

פתרון:
הכוח המשיקי לפי הספק נתון ע”י:

על גג”ש :

בהנחה שאין איבודי הספק במערכת (נצילות של ), נקבל:

סעיף ג’

חשב את רכיבי הכוחות הרדיאליים בין גג”ש ל- ובין גג”ש ל-.

פתרון:
את רכיבי הכוחות הרדיאליים ניתן לחשב באמצעות זוויות הלחץ (גאומטרייה):

מכאן:

סעיף ד’

חשב את הכוחות הפועלים על הציר של גג”ש .

פתרון:
נבצע מאזני כוחות סביב הצירים:

דג”ח על גג”ש .

משיווי משקל:

תרגיל 2

נתונה תמסורת בעלת יחס תמסורת . מספר השיניים בפיניון הוא והמודול הוא . רוחב התמסורת (רוחב השן) הינו . זווית הלחץ הינה .
מבחינה דינמית קבוצת איכות התמסורת הינה . הפיניון והגיר ממורכזים ביחס לגל שאותו הוא מניע והתמסורת הינה סגורה ומדויקת. לא מתוכנן תיקון דיוק לאחר ההרכבה.
התמסורת מונעת ע”י מנוע שריפה רב צילינדר בעל הספק של המסתובב במהירות של ומניעה מכונה המעמיסה באופן אחיד.

סעיף א’

מהו מאמץ הכפיפה לפי AGMA על הפיניון?

פתרון:
נחשב את כל אחד מהמקדמים:

  • הכוח המשיקי:
  • המקדם עומס יתר, מאחר ומדובר במנוע רב צילינדר:
  • מבחינת המקדם דינאמי, נצטרך את המהירות המשיקית: נחשב את המקדמים עבור : נחשב את המהירות המקסימלית עבור קבוצת איכות זו: ואכן המהירות המשיקית קטנה מהמקסימלית האפשרית.
    כעת, בהינתן , אנו יכולים לחשב את המקדם הדינאמי:
  • הפסיעה הינה , ולכן מקדם הגודל הינו:
  • מבחינת מקדם עובי הזר, נחשב את יחס הגיבוי . עבור גג”ש מלא, אנו יודעים לחשב את רדיוס המעגל העיקרי באופן הבא: ולכן המקדם:
  • מבחינת מקדם התפלגות העומס, מקדם תיקון הצורה, מאחר ואנו מניחים שאין הכתרה: מקדם יחס הפיניון, כיוון ש- , ניקח בחישוב של מקדם זה: נתון כי הפיניון והגיר ממורכזים בין המסבים, ולכן תיקונו: כדי לחשב את מקדם קוויות השילוב, נראה מהטבלה הרלוונטית שעבור תמסורת סגורה ומדויקת: ולכן: לא מתכונן תיקון דיוק לאחר ההרכבה ולכן .
    סוף סוף נוכל לחשב את מקדם התפלגות העומס:
  • את המקדם הצורה נשלוף מטבלה רלוונטית עבור מספר השיניים בגיר , שיניים בפיניון, וזווית לחץ של . נשים לב שאנו רוצים לחשב את המאמץ בפיניון, כך שנדע לבחור את השורה המתאימה בטבלה. לאחר אינטרפולציה:

נוכל כעת להציב הכל במשוואה (SH14-15) כדי לקבל:

סעיף ב’

מהו מאמץ הכפיפה לפי AGMA על הגיר?

פתרון:
הדבר היחיד ששונה בין הגג”שים הוא המקדם הגאומטרי:

כאשר נציב במשוואה (SH14-15):

סעיף ג’

נתון כי גלגלי השיניים עשויים מפלדה לא איכותית (Grade 1) בעלת קושיות של , טמפרטורת השמן הינה ונדרשת אמינות של . ידוע ששימוש התמסורת הוא לאפליקציות רגילות אולם עקב אי וודאויות בהפעלת התמסורת, ישנה דרישה למקדם ביטחון של לא פחות מ- לכשל בכפיפה. האם החלפת התמסורת אחרי מחזורים מונעת כשל בכפיפה?

פתרון:
לפי מאמץ כפיפה מותר, נצטרך למצוא את המקדמים:

קיבלנו , כלומר, החלפת התמסורת ב- מחזורים אכן תמנע כשל בכפיפה.

תרגיל 3

נתונה מערכת של גג”ש משופעות בעלי זווית נטייה של , זווית לחץ של ומודול של . בנוסף, מספר השיניים בפיניון ובגיר .

יש לחשב את הגדלים הבאים:

  1. המודולים בכיוונים השונים .
  2. קוטרי החלוקה של הפיניון והגיר .
  3. זווית הלחץ המשיקה .
  4. אורך כולל של קו המגע בשיניים משופעות .
  5. יחס חלוקת העומס .

פתרון:

  1. המודול הנורמלי הוא פשוט המודול שמוגדר: מבחינת המודול החזיתי והצירי, לפי גאומטרייה של גלגל שיניים משופעות: וגם:
  2. מבחינת קוטרי החלוקה, הוא כעת נקבע לפי המודול החזיתי : מבחינת הגיר:
  3. את זווית הלחץ המשיקית אנו מחשבים לפי:
  4. לפי אורך מגע בגג”ש משופעות: מבחינת רדיוסי החלוקה, הם פשוט ו- . מבחינת רדיוסי הבסיס: נציב הכל ונקבל:
  5. את יחס חלוקת העומס אנו מחשבים באופן הבא: כאשר הוא פסיעת הבסיס במישור הנורמלי, שבגג”ש ישרות: נציב ונקבל:

תרגיל 4

נתנוה תמסורת גג”ש משופעות בעלת הנתונים הבאים:

הגג”ש עשוי פלדה Grade 1 ו-. טמפרטורת העבודה הינה .

התמסורת מיוצרת באיכות הגבוהה ביותר, מיועדת לשימושים קריטיים, מותקנת בקופסה סגורה בצורה מדויקת ללא תיקונים לאחר ההתקנה. לפיניון יש סטייה ממרכוז של . המנוע הוא מנוע רב צילינדרי, משטר ההלמים ביציאה הוא בינוני. התכן נעשה עבור אמינות של . באמצעות התמסורת מועבר הספק ובמהירות של . אין דרישה למקדם ביטחון נוסף מעבר לתקן.

סעיף א’

כעבור כמה זמן תכשל התמסורת ומה יהיה סוג הכשל?

פתרון:
נביט במשוואה (SH14-15):

נרצה לדעת עבור איזה מתקיים שהמאמץ כפיפה הוא מתחת למאמץ הכפיפה המותר:

כלומר, מהתנאי נחלץ מהו המותר.
נצטרך כמובן גם לבדוק מאמץ מגע:

והאם הוא מתחת למאמץ מגע מותר:

כיוון שהגג”שים עשויים מאותו חומר, ניתן לבדוק את חוזק הפיניון בלבד.

נשים לב שלפי גאומטריית גג”ש משופעות:

נחשב את כל אחד מהמקדמים:

  • העומס על הגג”ש, בהנחה ואין איבוד הספק:
  • המקדם עומס יתר, מאחר ומדובר במנוע רב צילינדרי - משטר הלמים בינוני, נקבל:
  • מבחינת המקדם הדינאמי, כיוון שהתמסורת עשויה מהאיכות הגבוהה ביותר , אין מגבלת מהירות והמקדם הדינמי הינו:
  • הפסיעה בפיניון מקיימת , ולכן מקדם הגודל הינו:
  • מבחינת מקדם עובי הזר, נחשב את יחס הגיבוי . עבור גג”ש מלא, אנו יודעים לחשב את רדיוס המעגל העיקרי באופן הבא: ולכן המקדם לשניהם:
  • מבחינת מקדם התפלגות העומס, מקדם תיקון הצורה, מאחר ואנו מניחים שאין הכתרה: מבחינת מקדם יחס הפיניון, כיוון ש- , אנו יודעים שעבור : נתון כי לפיניון יש סטייה ממרכוז של , ולכן תיקונו: כדי לחשב את מקדם קוויות השילוב, נראה מהטבלה הרלוונטית שעבור תמסורת סגורה ומדויקת: ולכן: לא מתכונן תיקון דיוק לאחר ההרכבה ולכן .
    סוף סוף נוכל לחשב את מקדם התפלגות העומס:
  • החוזק לכפיפה עבור Grade 1 ו- הינו:
  • המקדם אמינות:
  • ניקח מקדם טמפרטורה .
  • נבחר מקדם ביטחון לכפיפה .
  • מבחינת מקדם מספר מחזורים לכפיפה, עבור תמסורת לשימושים קריטיים:

נזכור כי אנו רוצים לקיים :

לאחר הצבת כל המקדמים ב- והשאר, נקבל:

מבחינת כשל במגע, המקדמים:

נזכור כי אנו רוצים לקיים :

לאחר הצבת כל המקדמים ב- והשאר, נקבל:

לכן הכשל המוקדם יותר הוא כשל במגע.

סעיף ב’

התמסורת מהווה חלק ממכלול מכני. איזה שינוי אתם מציעים לעשות על מנת להבטיח את תקינות התמסורת לאורך מחזורים?

פתרון:
כיוון שהתמסורת מהווה חלק ממכלול מכני, לא ניתן לשנות את ממדיה, אבל כן ניתן להגדיל את הקשיות שלה. על מנת למנוע כשל במגע עבור מחזורים:

נדרוש:

נציב נתונים:

עבור פלדה Grade 1, זה אומר:

לכן, אם יתבצע חיסום ל- , ניתן יהיה לעמוד ביעד שהוגדר.

עמודים המציינים את העמוד הזה