NUM1_002 שיטות ישירות לפתרון מערכות לינאריות

ישנם המון שיטות לפתירת מערכת משוואות לינארית.
נעבור על מספר שיטות, הסיבוכיות שלהן, והיתרונות והחסרונות של כל אחת.

אלגוריתם: שיטת האלימינציה של גאוס

• ניזכר באלימינציה של גאוס מאלגברה לינארית.

בהינתן מערכת משוואות לינארית נוכל לרשום אותה בצורה הבאה:

בשיטת האלימינציה של גאוס, אנחנו ראשית מדרגים את המטריצה, ואז מבצעים חילוץ לאחור (backward sweep):

1. נרחיב את מטריצה בעוד עמודה שתכלול את ערכי :
2. נחליף את השורות באופן כזה שאיבר יהיה האיבר הגדול ביותר (בערכו המוחלט) בעמודה הראשונה.
3. ניצור עמודת אפסים מתחת לאיבר ע”י:
   • חיסור מהשורה השנייה (כאשר ב- הכוונה לשורה הראשונה).
   • חיסור מהשורה השלישית.
   • חיסור מהשורה ה--ית.
   נקבל:
4. נחזור על שלבים 2-3 על התת-מטריצה מסדר של שמתקבלת אם נתעלם מהשורה והעמודה הראשונה שלה. כתוצאה מכך אנחנו נסיים את דירוג המטריצה ונקבל מטריצה משולשת עליונה:
5. נפתור עבור , כאשר נתחיל מהאיבר לפי הנוסחה הבאה: כאשר היא המטריצה .

ב-pseudocode:

h := 1 /* Initialization of the pivot row */
k := 1 /* Initialization of the pivot column */
 
while h ≤ m and k ≤ n
	/* Find the k-th pivot: */
	i_max := argmax (i = h ... m, abs(A[i, k]))
	if A[i_max, k] = 0
		/* No pivot in this column, pass to next column */
		k := k + 1
	else
		swap rows(h, i_max)
		/* Do for all rows below pivot: */
		for i = h + 1 ... m:
			f := A[i, k] / A[h, k]
			/* Fill with zeros the lower part of pivot column: */
			A[i, k] := 0
			/* Do for all remaining elements in current row: */
			for j = k + 1 ... n:
				A[i, j] := A[i, j] - A[h, j] * f
		/* Increase pivot row and column */
		h := h + 1
		k := k + 1
 

כאשר סוכמים את מספר הפעולות שעושים בשיטה זו, מקבלים כי בסך הכל מבצעים פעולות. לכן מסווגים את שיטת האלימינציה עם סיבוכיות .

אלגוריתם: שיטת תומס למטריצות תלת אלכסוניות

הגדרה:

מטריצה תלת אלכסונית היא מטריצה מהצורה:

בהינתן מערכת משוואות כך ש- היא מטריצה תלת אלכסונית, נוכל לפתור אותה בשיטת תומאס בסיבוכיות .

השיטה מורכבת משני שלבים:

1. שיטת הליכה לפנים (forward sweep):
   על השורה הראשונה נבצע: ועל כל שורה אחרת: בסוף התהליך אנחנו נקבל מטריצה משולשת עליונה עם -ים על האלכסון:
2. נבצע חילוץ לאחור:
   נפתור עבור , כאשר נתחיל מהאיבר לפי הנוסחה הבאה:

אלגוריתם: פירוק LU

נביט בשלב השלישי של אלימיניציית גאוס. אנחנו מאפסים את כל האיברים מתחת ל-, כאשר כל הפעולות שאנחנו עושים על השורות מתבצעות גם על העמודה הכי ימנית - וקטור . נשים לב שאת פעולות אלו אנחנו למעשה יכולים לעשות בזמן יותר מאוחר, כי הם לא משפיעות על המטריצה .
את כל הפעולות האלו אנחנו יכולים לייצג בעזרת מטריצה משולשת עליונה (זה בעצם סוג של מטריצה אלמנטרית):

כלומר, לאחר איפוס העמודה הראשונה, נוכל לרשום את המטריצה והוקטור שמתקבלים כך:

באותו אופן נמשיך פעמים עד שנקבל את המטריצה המדורגת שלנו (מטריצה משולשת עליונה). נסמן אותה ב-:

באותו אופן עבור :

אם נפעיל את הפעולות ההפוכות () על בחזרה, אנחנו נקבל את המטריצה המקורית שלנו, :

נסמן את המכפלת מטריצות הארוכה ב-:

ונקבל:

מה שביצענו כאן נקרא פירוק LU - פירקנו את המטריצה למכפלת מטריצה משולשת תחתונה במטריצה משולשת עליונה.

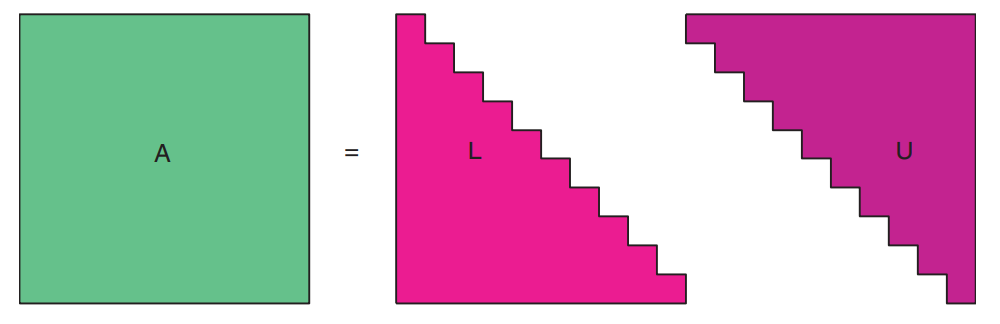
כדי להבין איך נראה, נשים לב ש- בעל בדיוק אותה צורה כמו , רק הפעם האיברים שלו ללא סימן המינוס. אז למשל עבור , ההופכי שלו נראה כך:

לכן המכפלה של כל המטריצות האלו נראית כך:

סדר הפעולות עבור פירוק מטריצה הוא כך:

1. מבצעים את הכפל מטריצות, כאשר את המשוואות מתחילים לפתור מה-”ר” החיצוני ל-”ר” הפנימי, כאשר תמיד נפתור קודם את האלמנט הפינתי.
2. נפתור את המערכת היותר פשוטה ע”י חליצה לפנים (כמו “חליצה לאחור”, אבל הפוך):
3. נפתור את המערכת הבאה ע”י חליצה לאחור:

הערה:

אין משמעות לכך שאלכסון ה--ים יהיה דווקא במטריצת ולא ב-. למעשה מבדילים בין שני המקרים בשמות שונים.
כאשר אנו קובעים ש- אנחנו קוראים לשיטה זו שיטת Crout.
כאשר אנו קובעים ש- אנחנו קוראים לשיטה זו שיטת Doolittle.

קוד ב-MATLAB:

function LU = LUDecompDoolittle(A)
	n = length(A);
	LU = A;
	% decomposition of matrix, Doolittle's Method
	for i = 1:1:n
		for j = 1:(i - 1)
			LU(i,j) = (LU(i,j) - LU(i,1:(j - 1))*LU(1:(j - 1),j)) / LU(j,j);
		end
		j = i:n;
		LU(i,j) = LU(i,j) - LU(i,1:(i - 1))*LU(1:(i - 1),j);
	end
	%LU = L+U-I
end
 
function x = SolveLinearSystem(LU, B)
	n = length(LU);
	y = zeros(size(B));
	% find solution of Ly = B
	for i = 1:n
		y(i,:) = B(i,:) - LU(i,1:i)*y(1:i,:);
	end
	% find solution of Ux = y
	x = zeros(size(B));
	for i = n:(-1):1
		x(i,:) = (y(i,:) - LU(i,(i + 1):n)*x((i + 1):n,:))/LU(i, i);
	end	
end

מבחינת סיבוכיות, יש בפירוק LU את אותו מספר פעולות כמו בגאוס. לכן גם לפירוק LU סיבוכויות . אך הפעם, מאחר ולא הכללנו את בכל החישובים שלנו, אנחנו יכולים לשמור את המטריצות ו- במקרה ונרצה לחשב יותר מהר עבור אחר.

אלגוריתם: פירוק שולסקי

עבור מטריצות סימטריות שהן מוגדרות חיובית נוכל לבצע פירוק LU בסיבוכיות יותר טובה, הנקרא פירוק שולסקי (Cholesky). במקרה כזה אנחנו יכולים למצוא מטריצה יחידה שהיא:

• משולשת תחתונה
• עם איברים חיוביים וממשיים על האלכסון
• מתקיים:

דוגמה:

במקרה של מטריצה מסדר , נניח כי מטריצה כזאת קיימת:

כעת יש לנו שלושה משוואות בשלושה נעלמים:

הסיבוכיות של אלגוריתם זה היא גם , אבל היא דורשת פחות פעולות חישוב סך הכל.
עבור פירוק LU, מתבצעים חישובים. לעומת זאת, בפירוק שולסקי, מתבצעים חישובים.