פנגייה

NUM1_003 נורמה

• זמן קריאה: 5 דק'

השגיאות שעסקנו בהם בנושאים קודמים נותנים לנו את השגיאות של סקלר מסוים. מאחר ואנחנו מתכוונים לחשב מטריצות ווקטורים, נרצה דרך למדוד “מרחקים” בין וקטורים ומטריצות. הנורמה היא הרחבה של רעיון הערך מוחלט (או גודל) לוקטורים ומטריצות.

נורמה של וקטור

עבור וקטור , האורך האוקלידי שלו מוגדר כ:

האורך האוקלידי הוא סוג של נורמה. ספציפית, הוא ההנורמה 2 של הוקטור ונעזרים בו כדי למדוד את אורכו. ישנם עוד סוגים של נורמות:

  • נורמת האינסוף - הרכיב הכי גדול בוקטור :
  • הנורמה 1 - סכום כל הרכיבים של הוקטור :

ההגדרה של נורמה היא מאוד כללית:

הגדרה:

נורמה היא פונקציה על רצף של מספרים סקלרים, המסומנת ב-, ומקיימת את התנאים הבאים:
1.

הנורמות שהראינו בהתחלה הם כולם מקרים מיוחדים של משפחת נורמות המוגדרות:

דוגמה:

נניח ואנחנו נרצה למצוא את המרחק בין שני וקטורים:

אז נגדיר:

אז מתקיים:

למרות שהערכים של הנורמות שונים, הם בעלי אותו הסדר גודל.

ניתן לראות בדוגמה האחרונה שמתקיים:

טענה זו נכונה בכללית. מעבר לכך, ניתן להוכיח כי לכל מתקיים:

האיור הבא מראה את כל הוקטורים ב- שהנורמות שלהם שווים ל-, לפי כל אחד מהנורמות שראינו:
book

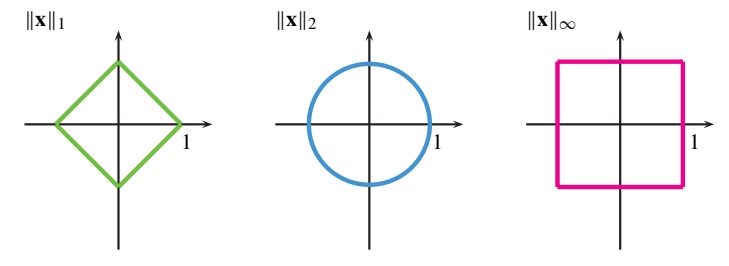
“מעגל היחידה” לפי כל אחד מהנורמות. נשים לב שהמעוין כלול בתוך העיגול, שהוא בעצמו כלול בתוך הריבוע.

נורמה של מטריצה

ניזכר מאלגברה לינארית מהי מטריצה סינגולרית. בגדול, מטריצה לא הפיכה היא מטריצה סינגולרית.

נורמה של מטריצה היא כלי שנותן לנו מדד לכמה מטריצה רחוקה מסינגולריות, ובכך למדוד את יציבות האלגוריתם שלנו.

אנו בהגדרת נורמה של מטריצה שהיא מושרית מהגדרת הנורמה לוקטור. לכן היא נקראת נורמה מושרית:

הגדרה: הנורמה המושרית של מטריצה מוגדרת כך:

לא קשה להראות שהנורמה המושרית עומדת בכל התנאים להגדרה של נורמה. מעבר לכך, היא עומדת בתנאי העקביות:

בפרט, עבור כל וקטור בעל הממדים הנכונים, מתקיים:

נחשב כעת את נורמה-, נורמה- ונורמה- של מטריצה כללית, כדי לקבל נוסחאות יותר מקוצרות עבור כל אחת:

נורמה-

יהי וקטור כך ש-. לפיכך, מתקיים:

לכן, לפי נורמה- של וקטור:

נבחר אינדקס שהוא אינדקס השורה בעלת סכום הערכים המוחלטים הכי גדול ב-:

ולכן נוכל לרשום את (1) כך:

נבחר כעת אחר, כך ש:

נקבל מכך ש:

אז עבור מתקיים:

מאחר ומתקיים האי שוויון , נוכל לשלב את (2) ו-(3):

נקבל כי מתקיים שוויון לאורך כלל האי שוויון:

כלומר, הנורמה- של היא הסכום המקסימלי של איברים בשורה.

נורמה-

נוכל באותה צורה להגיע למסקנה כי:

כלומר, הנורמה- של היא הסכום המקסימלי של איברים בעמודה.

נורמה- - רדיוס ספקטרלי

כדי לחשב את הנורמה- של מטריצה, אנחנו צריכים לקחת בחשבון את הערכים העצמיים של המטריצה .

הגדרה:

תהי מטריצה ריבועית , כך שיש לה ע”ע. הרדיוס הספקטרלי של מוגדר כ:

אם הם זוג ע”ע וו”ע כך ש- מקסימלי ל-, ו- מנורמל כך ש-, אז:

לכן, כל נורמה מושרית חסומה מלמטה ע”י הרדיוס הספרטרלי!

הערה:

רדיוס ספקטרלי של מטריצה ריבועית הוא לא הנורמה שלו.

ניתן להראות (בעזרת הוכחה שלא ניכנס אליה) שעבור מטריצות שהן לא בהכרח ריבועיות (כלומר מסדר ), מתקיים:

כאשר נשים לב ש- היא בהכרח מטריצה סימטרית (ריבועית) עם ע”ע חיוביים, , וממשפט שלא נוכיח אותו, הו”ע אורתוגונליים.

בצורה אינטואיטיבית, אפשר לחשוב על הנורמה-, שנקראת גם הנורמה הספקטרלית, כה’הגדלה’ המקסימלית שמטריצה יכולה להפעיל על וקטור (אם חושבים על מטריצה כטרנספורמציה לינארית).

מספר מצב

מספר מצב של פונקציה מסוימת מודדת כמה התוצאה של הפונקציה משתנה ביחס לשינוי קטן בקלט שלה. כלומר, מספר מצב מתאר את היציבות של פונקציה כשלהי.

במערכת משוואות לינארית , המספר מצב נותן חסם עליון לכמה הניחוש יהיה קרוב לפתרון האמיתי .
נשים לב שמספר מצב זוהי תכונה של המטריצה, ולא של האלגוריתם או הדיוק המספרי של המחשב שמחשב את התשובה.

ניתן לחשוב על מספר מצב כהמידה בה הפתרון ישתנה כתוצאה משינוי ב-. לכן, אם מספר המצב גדול, אפילו שינוי קטן ב- יגרום לשגיאה גדולה ב-.

הגדרה:

מספר מצב של מטריצה מוגדר כ:

הערה:

בעת חישוב של מספר המצב יש להשתמש באותו סוג נורמה לחישוב המטריצה והמטריצה ההופכית.

נביט במערכת משוואות . בהינתן ניחוש של הפתרון , נוכל לחסום את השגיאה היחסית.
השגיאה האבסולוטית והשארית נתונים ע”י:

החסמים לשגיאה היחסית נתונים ע”י הנוסחה הבאה:

עמודים המציינים את העמוד הזה