NUM1_005 משוואות לא לינאריות במשתנה אחד

→ קודם: NUM1_004הבא: NUM1_006 ←

מבוא

פרק זה עוסק במציאת פתרונות למשוואה הסקלרית, הלא לינארית:

כאשר נמצא בטווח . נניח תמיד שהפונקציה רציפה על הקטע (), ונסמן את הפתרון של הפונקציה ב-, כאשר נקרא לו שורש.

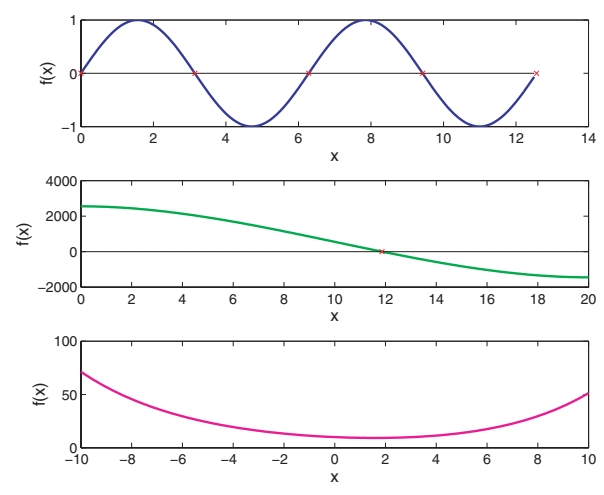
גרף של שלושה פונקציות והשורשים שלהם.

שיטת החצייה

השיטה הבאה, שהיא בעצם אנלוגית לחיפוש בינארי, היא פשוטה ודורשת מעט מידע על הפונקציה . אבל, היא איטית ומסובך להכליל אותה למקרים רב ממדיים.

נניל ועבור נתון אנו יודעים על תחום בו משנה סימן. משפט ערך הביניים מבטיח לנו שקיים שורש כך ש- . כעת, נחשב את , כאשר

הוא החציון, ונבדוק את הסימן של המכפלה . אם היא שלילית, אז השורש נמצא בקטע , אז אנחנו יכולים להציב ולחזור על הפעולה.
אם חיובית, אז השורש נמצא על הקטע , אז נציב ונחזור על הפעולה.
אנחנו נעצור את האלגוריתם כאשר , ואז נסיק כי .

בכל איטרציה על הקטע בו נמצא, הקטע קטן פי , ולכן השיטה נקראת שיטת החצייה. באיטרציה ה--ית, מתקיים . לכן, האלגוריתם מחויב להתכנס.

שיטת ניוטון ו-Secant

שיטת החציון רק דורשת שהפונקציה תהיה רציפה (שזה סבבה והכל) ולא צריכה יותר מדי אינפורמציה על נגזרות הפונקציה, או אפילו על הקיום שלהן.

שיטת ניוטון דורשת יותר מידע על חלקלקות הפונקציה, אבל היא מתכנסת הרבה יותר מהר לשורש.

אלגוריתם: שיטת ניוטון

שיטה זו היא הדרך המהירה הבסיסית ביותר למציאת שורש. הרעיון שעומד מאחוריו ניתן להכללה כדי לפתור בעיות יותר כלליות.

נניח שהנגזרת הראשונה והשנייה של קיימות ורציפות (. נניח גם שניתן לחשב את יחסית בקלות. לפי פיתוח טיילור עבור , אנחנו יכולים לרשום:

כאשר היא נקודה (לא ידועה) בין נקודה לנקודה .
אם , אז . אם היתה לינארית, אז , ואז נוכל למצוא את השורש כאשר נפתור

ונקבל:

לפונקציה לא לינארית נגדיר את האיטרציה הבאה ע”י אותה הנוסחה:

אנחנו מתעלמים מהביטוי בכל איטרציה לא רק כי אנחנו לא יודעים לחשב אותו, אלא גם כי הוא זניח יותר ויותר ככל שאנחנו מתקרבים לשורש (הביטוי קטן מאוד מהר).

מבחינה גאומטרית, הוא המפגש של המשיק ל- ב- עם ציר ה-:

---

תרגיל:
פתרו בעזרת שיטת ניוטון את אחד מהשורשים של הפונקציה הבאה:

עם הניחוש ההתחלתי:

פתרון:
הנגזרת:

לפי הנוסחה:

נוכל להתחיל לחשב איטרציות:

---

תרגיל:
על מנת לחשב עבור , מוצע להשתמש בשיטת ניוטון ולחשב שורש של פונקציה:

1. רשום ביטוי מפורש באמצעותו יחושבו הקירובים עבור .
   פתרון:
   הנגזרת: ולפי הנוסחה לאיטרציה:
2. האם מובטחת התכנסות של שיטת ניוטון במקרה הנתון ללא תלות בניחוש ההתחלתי?
   פתרון:
   נראה מה קורה:
   • כאשר :
     $$
     {x}{1} ={x}{0} (2-a{x}_{0} )<0 נקבלשתמיד
     • כאשר :
     • כאשר :
     • כאשר :
     • כאשר :
     ולכן נסיק כי: נוכל להמשיך באינדוקציה ולקבל: לכן, נוכל להוכיח שהסדרה בעצם עולה: הסדרה חסומה מלמעלה ומונוטונית ולכן מתכנסת. נוכיח כי ההתכנסות היא אל : לכן הגבול: נציב ש-:

אלגוריתם: שיטת Secant

הדרישה בשיטת ניוטון שלא רק הפונקציה אלא גם הנגזרת שלה תהיה נתונה לפעמים מתקיימת. אבל, לא תמיד נוכל לחשב את הנגזרת, או שלפעמים יהיה יותר מסובך לחשב את הנגזרת מאשר את עצמה.

שיטת Secant היא וריאציה של שיטת ניוטון, כאשר מוחלף ע”י קירוב סופי שתלוי בפונקציה בנקודה ואיטרציה קודמת . בהנחה וישנה התכנסות:

כאשר מציבים את קירוב זה בתוך הנוסחה של שיטת ניוטון, אנחנו מקבלים את השיטת Secant:

קצב ההתכנסות וסדר השגיאה

כמה מהר איטרציה מתכנסת, אם בכלל?

הגדרה:

נאמר כי סדרת איטרציות שמתכנסת לפתרון בעלת קצב התכנסות וסדר שגיאה אם:

אם , נאמר כי השיטה מתכנסת לינארית.
אם , נאמר כי השיטה מתכנסת ריבועית.
אם , נאמר כי השיטה מתכנסת סופרלינארית.

הערה:

אין הבהרה ברורה בין סדר שגיאה וקצב התכנסות בספרות. לפעמים בכלל קוראים ל- קצב ההתכנסות, או סדר ההתכנסות.

עבור שיטת החצייה, ניתן להראות כי השגיאה חסומה ע”י , ולכן:

כלומר, לשיטת החצייה יש קצב התכנסות , וסדר שגיאה , כלומר היא מתכנסת לינארית.

עבור שיטת ניוטון, אפשר להראות שאם וקיים שורש ב- כך ש- , אז קיימת סביבה של שאם נתחיל עם בסביבה זו, אז שיטת ניוטון מתכנסת ריבועית.

חישוב סדר השגיאה

לפעמים נרצה למצוא את סדר השגיאה בצורה נומרית. חישוב סדר השגיאה בצורה זו הוא אמנם לא מדויק, אבל הוא מאמת בסטייה מסוימת את קצבי ההתכנסות התאורתיים.
לאחר “מספיק” איטרציות, נוכל לראות מהגדרת הסדר שגיאה ש:

נוציא כדי שנוכל לבודד את :

אבל משוואה זו תקפה רק אם אנו באמת יודעים מהו הפתרון. נוכל לשער את סדר השגיאה גם אנו לא יודעים מהו הפתרון, אם אנו מניחים כי אחרי מספיק איטרציות מתקיים:

נציב זאת בנוחסה שקיבלנו ל- כדי לקבל:

→ קודם: NUM1_004הבא: NUM1_006 ←