PHY3_002 מבוא לפיזיקה קוונטית ב

→ קודם: PHY3_001הבא: PHY3_003 ←

תכונות הגל של חלקיקים

סטודנטים שלומדים בפעם הראשונה על הטבע הדואלי של האור לעתים קרובות מוצאים את המושג קשה לקבלה. בעולם סביבנו, אנחנו רגילים לראות דברים כמו כדורי בייסבול אך ורק כחלקיקים, ודברים אחרים כמו גלי קול אך ורק כצורות של תנועת גלים. כל תצפית בקנה מידה גדול יכולה להיות מפורשת על ידי שיקול הסבר גלי או הסבר חלקיקי, אבל בעולם של פוטונים ואלקטרונים, הבחנות כאלה אינן מצוירות בחדות כזו.

אפילו יותר מטריד הוא שבתנאים מסוימים, הדברים שאנחנו קוראים להם “חלקיקים” מפגינים מאפייני גלים! בעבודת הדוקטורט שלו משנת 1923, לואי דה ברויי הניח שמכיוון שלפוטונים יש מאפייני גל וחלקיק כאחד, אולי לכל צורות החומר יש את שתי התכונות. לרעיון המהפכני ביותר הזה לא היה שום אישוש ניסיוני באותו הזמן.

על פי דה ברויי, לאלקטרונים, בדיוק כמו לאור, יש טבע דואלי חלקיק-גל. על ידי שילוב משוואות (SJ38.28), (SJ39.5), ו- (מתוך פיזיקה 2), אנו מוצאים שהתנע של פוטון יכול להיות מבוטא כ:

משוואה זו מראה שאורך הגל של הפוטון יכולה להיות מוגדרת על ידי התנע שלו: . דה ברויי הציע שלחלקיקים חומריים בעלי תנע יש הם אורך גל אופייני הנתון באותו ביטוי.

מכיוון שגודל התנע של חלקיק במסה ומהירות הוא , אורך הגל של דה ברויי של אותו חלקיק הוא:

יתר על כן, באנלוגיה לפוטונים, דה ברויי הניח שחלקיקים מצייתים ליחס איינשטיין , כאשר היא האנרגיה הכוללת של החלקיק. לפיכך התדירות של חלקיק תהיה:

הטבע הדואלי של החומר ברור במשוואות (SJ39.15) ו-(SJ39.16) מכיוון שכל אחת מכילה מאפייני חלקיק ( ו-) ומאפייני גל ( ו-).

הבעיה של הבנת הטבע הדואלי של חומר וקרינה קשה מבחינה רעיונית מכיוון ששני המודלים נראים סותרים זה את זה. הבעיה הזו כפי שהיא חלה על אור נדונה קודם לכן.

עקרון ההשלמה קובע שמודלי הגל והחלקיק של חומר או קרינה משלימים זה את זה. אף מודל לא יכול לשמש באופן בלעדי לתיאור חומר או קרינה בצורה מספקת. מכיוון שבני אדם נוטים ליצור דימויים מנטליים על בסיס החוויות שלהם מהעולם היומיומי, אנו משתמשים בשני התיאורים באופן משלים כדי להסביר כל קבוצה נתונה של נתונים מהעולם הקוונטי.

ניסוי דייוויסון-גרמר

ההצעה של דה ברויי משנת 1923 שחומר מפגין תכונות גל וחלקיק כאחד נחשבה לספקולציה טהורה. אם לחלקיקים כמו אלקטרונים היו תכונות גל, בתנאים הנכונים הם צריכים להפגין השפעות דיפרקציה.

רק שלוש שנים מאוחר יותר, C. J. דייוויסון (1881–1958) ו-L. H. גרמר (1896–1971) הצליחו לצפות בדיפרקציית אלקטרונים ולמדוד את אורך הגל של אלקטרונים. הגילוי החשוב שלהם סיפק את האישור הניסיוני הראשון לגלים שהוצעו על ידי דה ברויי.

הכוונה של ניסוי דייוויסון-גרמר הראשוני לא הייתה לאשר את השערת דה ברויי. למעשה, הגילוי שלהם נעשה במקרה (כפי שקורה לעתים קרובות). הניסוי כלל פיזור של אלקטרונים באנרגיה נמוכה (בערך ) ממטרת ניקל בוואקום.

במהלך ניסוי אחד, משטח הניקל התחמצן קשות בגלל שבר מקרי במערכת הוואקום. לאחר שהמטרה חוממה בזרם של מימן כדי להסיר את ציפוי התחמוצת, אלקטרונים שהתפזרו על ידיה הראו שיאי ושפלי עוצמה בזוויות ספציפיות.

זמן קצר לאחר מכן, דייוויסון וגרמר ביצעו מדידות דיפרקציה נרחבות יותר על אלקטרונים המפוזרים ממטרות גביש יחיד. הניסויים שלהם הראו לבסוף שהניקל יצר אזורים גבישיים גדולים בחימום ושהמישורים הממוקמים במרווחים אחידים של אטומים באזורים אלה שימשו כסריג דיפרקציה לאלקטרונים. התוצאות שלהם הראו באופן חד-משמעי את הטבע הגלי של אלקטרונים ואישרו את יחס דה ברויי .

באותה שנה, G. P. תומסון (1892–1975) מסקוטלנד גם צפה בדפוסי דיפרקציית אלקטרונים על ידי העברת אלקטרונים דרך רדידי זהב דקים מאוד. דפוסי דיפרקציה נצפו לאחר מכן בפיזור של אטומי הליום, אטומי מימן ונויטרונים. לפיכך, הטבע הגלי של חלקיקים התגבש בדרכים שונות.

דוגמה: אורכי גל עבור עצמים מקרוסקופיים

איור 2.1: סלע במסה נזרק במהירות של . מה אורך הגל של דה ברויי שלו?

פתרון:

נעריך את אורך הגל של דה ברויי באמצעות משוואה (SJ39.15):

אורך גל זה קטן בהרבה מכל פתח שדרכו הסלע יכול לעבור. לכן, לא נוכל לצפות בהשפעות דיפרקציה, וכתוצאה מכך, התכונות הגליות של עצמים בקנה מידה גדול לא ניתנות לצפייה.

מודל חדש: החלקיק הקוונטי

מכיוון שבעבר חשבנו על מודלי החלקיק והגל כנבדלים, עם מודלי ניתוח נפרדים לכל אחד, הדיונים שהוצגו בסעיפים הקודמים עשויים להיות מטרידים למדי. הרעיון שגם אור וגם חלקיקי חומר בעלי תכונות חלקיק וגל כאחד אינו מתאים להבדלה זו. עדויות ניסיוניות מראות, עם זאת, שהמסקנה הזו היא בדיוק מה שעלינו לקבל.

ההכרה בטבע הדואלי הזה מובילה למודל פשטני חדש, החלקיק הקוונטי, שהוא שילוב של מודל החלקיק ומודל הגל. במודל החדש הזה, ליֵשׁוּיוֹת הכלולים בה, יש מאפייני חלקיק וגל כאחד, ועלינו לבחור התנהגות אחת מתאימה - חלקיק או גל - כדי להבין תופעה מסוימת.

בסעיף זה, נחקור מודל זה באופן שעשוי לגרום לכם להרגיש נוח יותר עם הרעיון הזה. נעשה זאת על ידי הדגמה שישות המפגינה תכונות של חלקיק יכולה להיבנות מגלים.

בואו נזכיר תחילה כמה מאפיינים של חלקיקים אידיאליים וגלים אידיאליים. לחלקיק אידיאלי יש גודל אפס. לכן, מאפיין חיוני של חלקיק הוא שהוא מקומי במרחב. לגל אידיאלי יש תדירות יחידה והוא ארוך לאין סוף כפי שמציע האיור הבא.

איור 2.2: ב-(a): גל אידיאלי בתדירות יחידה מדויקת זהה בכל המרחב והזמן. (b): אם שני גלים אידיאליים עם תדירויות שונות מעט משולבים, נוצרים פעימות. האזורים במרחב שבהם יש הפרעה בונה שונים מאלה שבהם יש הפרעה הורסת. (Serway et al., 2019).

לכן, גל אידיאלי אינו מקומי במרחב. ישות מקומית יכולה להיבנות מגלים ארוכים לאין סוף כדלהלן.

דמיינו שרטוט של גל אחד לאורך ציר ה-, עם אחד מהפסגות שלו ממוקם ב-, כמו בחלק העליון של איור 2.1. כעת שרטטו גל שני, באותה משרעת אך בתדירות שונה, עם אחת מהפסגות שלו גם ב-. כתוצאה מעקרון הסופרפוזיציה של שני הגלים האלה, קיימות פעימות כאשר הגלים נמצאים לסירוגין בפאזה ומחוץ לפאזה. העקומה התחתונה באיור 2.1 מראה את התוצאות של סופרפוזיציה של שני הגלים הללו.

שימו לב שכבר הכנסנו מידה מסוימת של לוקליזציה על ידי סופרפוזיציה של שני הגלים. לגל יחיד יש את אותה משרעת בכל מקום במרחב; אף נקודה במרחב אינה שונה מכל נקודה אחרת. על ידי הוספת גל שני, עם זאת, יש משהו שונה בנקודות בפאזה בהשוואה לנקודות מחוץ לפאזה.

כעת דמיינו שיותר ויותר גלים שמתווספים לשני המקוריים שלנו, כל גל חדש בעל תדירות חדשה. כל גל חדש מתווסף כך שאחת מפסגותיו נמצאת ב- כך שכל הגלים מתחברים בצורה בונה ב-. כאשר אנו מוסיפים מספר גדול של גלים, ההסתברות לערך חיובי של פונקציית גל בכל נקודה שווה להסתברות לערך שלילי, ויש הפרעה הורסת בכל מקום מלבד ליד , שם כל הפסגות מופרות זו על זו. התוצאה מוצגת באיור הבא.

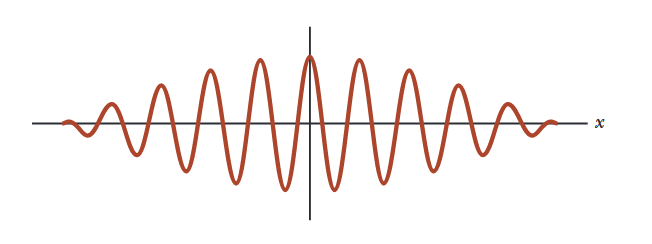
איור 2.3: אם מספר גדול של גלים משולבים, התוצאה היא צְרוֹר-גַּלִּים, המייצגת חלקיק. (Serway et al., 2019).

האזור הקטן של הפרעה בונה נקרא צרור גלים. אזור מקומי זה במרחב שונה מכל האזורים האחרים. אנו יכולים לזהות את חבילת הגלים כחלקיק מכיוון שיש לה את הטבע המקומי של חלקיק! המיקום של חבילת הגלים מתאים למיקום החלקיק.

הטבע המקומי של ישות זו הוא המאפיין היחיד של חלקיק שנוצר עם תהליך זה. לא התייחסנו לאיך חבילת הגלים עשויה להשיג מאפייני חלקיק כמו מסה, מטען חשמלי וספין. לכן, ייתכן שלא תהיו משוכנעים לחלוטין שבנינו חלקיק.

כעדות נוספת לכך שחבילת הגלים יכולה לייצג את החלקיק, בואו נראה שלחבילת הגלים יש מאפיין נוסף של חלקיק. כדי לפשט את הייצוג המתמטי, נחזור לשילוב של שני גלים.

שקלו שני גלים עם משרעות שוות אך תדירויות זוויתיות שונות ו-. אנו יכולים לייצג את הגלים מתמטית כ:

כאשר ו-. באמצעות עקרון הסופרפוזיציה, בואו נחבר את הגלים:

נוח לכתוב ביטוי זה בצורה המשתמשת בזהות הטריגונומטרית:

בהצבת ו- נקבל:

כאשר ו-. הגורם הקוסינוס השני מייצג גל עם מספר גל ותדירות השווים לממוצעים של הערכים עבור הגלים הבודדים.

במשוואה (SJ39.17), הגורם בסוגריים המרובעים מייצג את המעטפת של הגל כפי שמוצג על ידי העקומה המקווקוות באיור הבא.

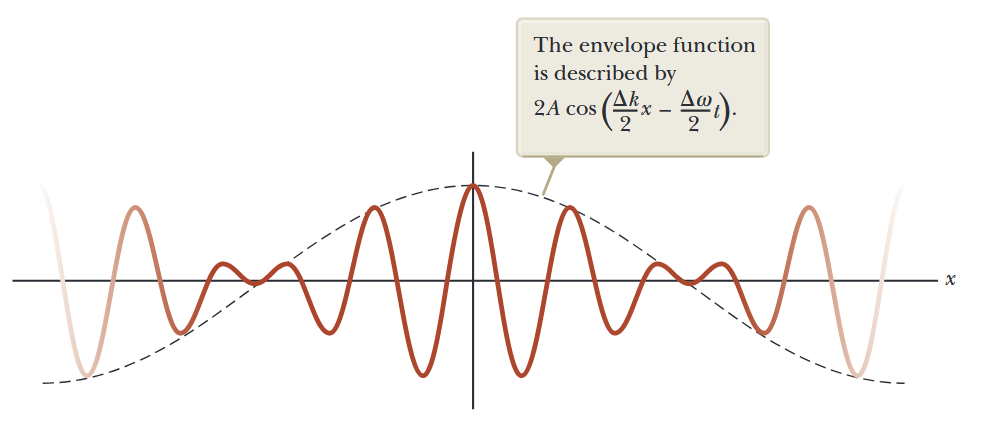
איור 2.4: תבנית הפעימות עם פונקציית מעטפת (עקומה מקווקוות) מוצבת מעל. פונקציית המעטפת מתוארת על ידי . (Serway et al., 2019).

לגורם זה גם יש את הצורה המתמטית של גל. המעטפת הזו יכולה לנוע במרחב במהירות שונה מהגלים הבודדים. כדוגמה קיצונית לאפשרות זו, דמיינו שילוב של שני גלים זהים הנעים בכיוונים מנוגדים. שני הגלים נעים באותה מהירות, אך למעטפת יש מהירות של אפס מכיוון שבנינו גל עומד.

עבור גל בודד, המהירות היא:

מהירות זו נקראת מהירות הפאזה מכיוון שהיא קצב ההתקדמות של פסגה על גל יחיד, שהיא נקודה של פאזה קבועה. משוואה (SJ39.18) יכולה להיות מפורשת כדלהלן: מהירות הפאזה של גל היא היחס של המקדם של משתנה הזמן למקדם של משתנה המרחב במשוואה המייצגת את הגל, .

הגורם בסוגריים במשוואה (SJ39.17) הוא בצורת גל, אז הוא נע במהירות הניתנת על ידי אותו יחס:

הסימון על המהירות מציינת שהיא נקראת בדרך כלל מהירות הקבוצה (group speed), או מהירות צרור הגלים (קבוצת הגלים) שבנינו. יצרנו ביטוי זה עבור חיבור פשוט של שני גלים. כאשר מספר גדול של גלים מופרים יחד ליצירת חבילת גלים, יחס זה הופך לנגזרת:

בהכפלת המונה והמכנה ב-, כאשר , נקבל:

נביט במונחים בסוגריים של משוואה (SJ39.20) בנפרד. עבור המונה:

עבור המכנה:

לכן, משוואה (SJ39.20) יכולה להיכתב כ:

מכיוון שאנו חוקרים את האפשרות שהמעטפת של הגלים המשולבים מייצגת את החלקיק, נניח חלקיק חופשי הנע במהירות שהיא קטנה בהשוואה למהירות האור. האנרגיה של החלקיק היא האנרגיה הקינטית שלו:

בגזירת משוואה זו ביחס ל- נקבל:

לכן, מהירות הקבוצה של חבילת הגלים זהה למהירות החלקיק שהיא ממודלת לייצג, מה שנותן לנו ביטחון נוסף שצרור הגלים היא דרך סבירה לבנות חלקיק.

ניסוי שני הסדקים - חזרה

העובדה שלאור ולחלקיקי חומר יש התנהגות גל וחלקיק כאחד נקראת דואליות גל-חלקיק. זהו כעת מושג מקובל המחוזק על ידי תוצאות ניסיוניות, כולל אלה של ניסוי דייוויסון-גרמר.

בואו נאתגר את הרעיונות הללו על ידי אמירה: “בסדר, אם לאלקטרונים יש מאפייני גל, תראו לי אלקטרונים בהפרעה!” זה אתגר נהדר! בואו נקים ניסוי ונראה מה קורה.

שקלו קרן מקבילה של אלקטרונים מונו-אנרגטיים הפוגעת בחריץ כפול כמו באיור הבא.

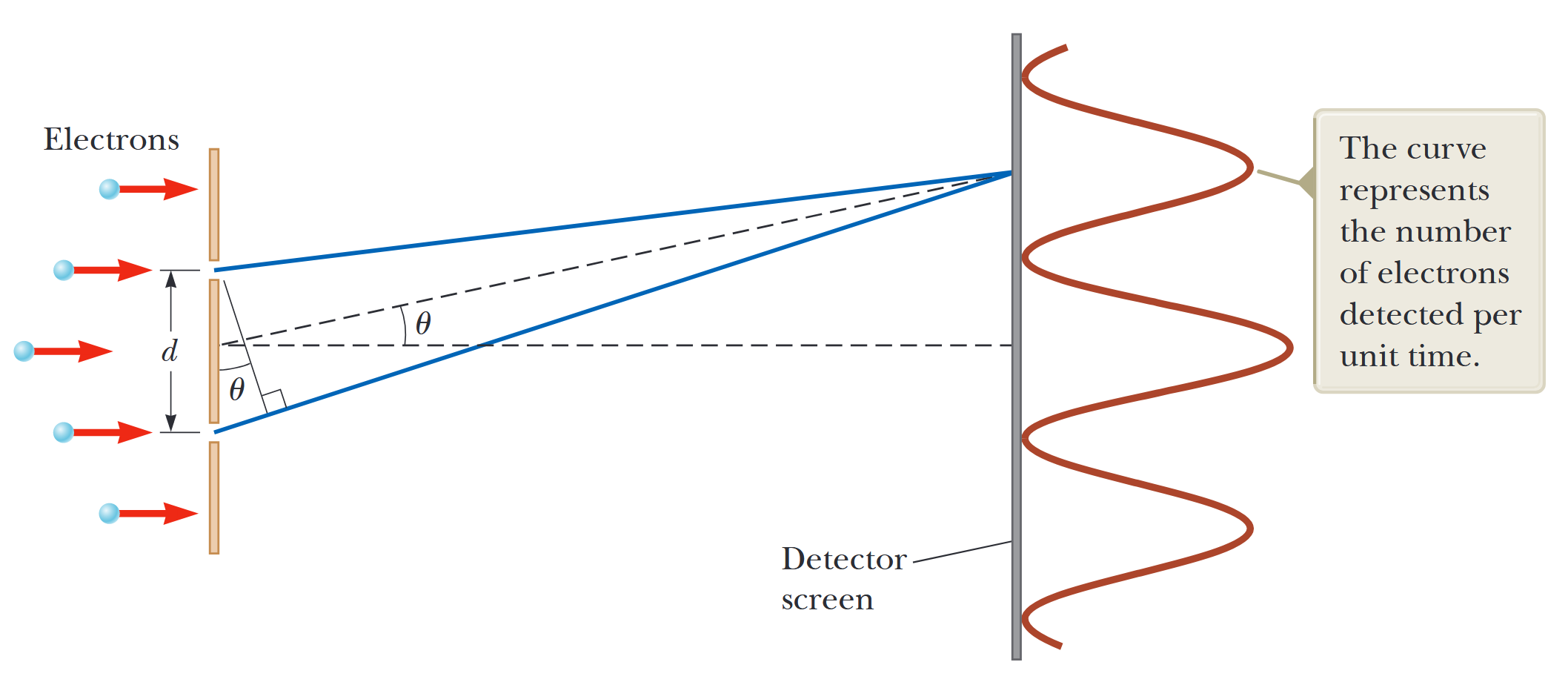
הפרעת אלקטרונים. הפרדת החריצים גדולה בהרבה מרוחבי החריצים הבודדים וקטנה בהרבה מהמרחק בין החריץ למסך הגלאי. העקומה מייצגת את מספר האלקטרונים שזוהו ליחידת זמן. (Serway et al., 2019).

בואו נניח שרוחבי החריצים קטנים בהשוואה לאורך הגל של האלקטרון כך שלא נצטרך לדאוג למקסימומי ומינימומי דיפרקציה. מסך גלאי אלקטרונים ממוקם רחוק מהחריצים במרחק הגדול בהרבה מ-, מרחק ההפרדה של החריצים.

אנו מפעילים את המכשיר ומחכים שפגיעות אלקטרונים יצטברו על המסך. לאחר מרווח זמן ארוך מספיק, אנו מוצאים תבנית הפרעת גלים! אם נמדוד את הזוויות שבהן העוצמה המקסימלית של אלקטרונים מגיעה למסך הגלאי באיור 2.4, אנו מוצאים שהן מתוארות על ידי בדיוק אותה משוואה כמו זו עבור אור:

כאשר הוא מספר הסדר ו- הוא אורך הגל של האלקטרון.

לכן, הטבע הדואלי של האלקטרון מוצג בבירור בניסוי זה: האלקטרונים מזוהים כחלקיקים בנקודה מקומית על מסך הגלאי ברגע מסוים בזמן, אבל ההסתברות להגעה לאותה נקודה נקבעת על ידי מציאת העוצמה של שני גלים מפריעים!

כעת דמיינו שאנו מורידים את עוצמת הקרן כך שאלקטרון אחד בכל פעם מגיע לחריץ הכפול. מפתה להניח שהאלקטרון עובר דרך חריץ 1 או חריץ 2. אתם עלולים לטעון שאין השפעות הפרעה כיוון שאין אלקטרון שני העובר דרך החריץ השני כדי להפריע לראשון. ההנחה הזו שמה יותר מדי דגש על מודל החלקיק של האלקטרון.

תבנית ההפרעה עדיין נצפית אם מרווח הזמן למדידה ארוך מספיק כדי שאלקטרונים רבים יעברו אחד בכל פעם דרך החריצים ויגיעו למסך הגלאי! המצב הזה מוצג על ידי התבניות המדומות במחשב באיור הבא.

ב- (c)-(a) תבניות הפרעה מדומות במחשב עבור מספר קטן של אלקטרונים הפוגעים בחריץ כפול. לאחר 28 אלקטרונים בלבד, לא מופיעה תבנית. לאחר 1000 אלקטרונים, תבנית של פסים מתחילה להופיע. לאחר 10,000 אלקטרונים, התבנית נראית דומה מאוד לתוצאה הרב-אלקטרונית המוצגת ב-(d). (d) הדמיה במחשב של תבנית הפרעת חריץ כפול המיוצרת על ידי אלקטרונים רבים. (Serway et al., 2019).

תבנית ההפרעה הופכת ברורה יותר ככל שמספר האלקטרונים המגיעים למסך הגלאי עולה. לכן, ההנחה שלנו שהאלקטרון מקומי ועובר רק דרך חריץ אחד כאשר שני החריצים פתוחים חייבת להיות שגויה (מסקנה כואבת!).

כדי לפרש תוצאות אלה, אנו נאלצים להסיק שאלקטרון מקיים אינטראקציה עם שני החריצים בו-זמנית. אם תנסו לקבוע בניסוי דרך איזה חריץ האלקטרון עובר, פעולת המדידה הורסת את תבנית ההפרעה. אי אפשר לקבוע דרך איזה חריץ האלקטרון עובר. למעשה, אנו יכולים לומר רק שהאלקטרון עובר דרך שני החריצים! אותם טיעונים חלים על פוטונים.

אם אנו מגבילים את עצמנו למודל חלקיק טהור, זהו רעיון לא נוח שהאלקטרון יכול להיות נוכח בשני החריצים בו-זמנית. ממודל החלקיק הקוונטי, עם זאת, החלקיק יכול להיחשב כבנוי מגלים הקיימים בכל המרחב. לכן, רכיבי הגל של האלקטרון נוכחים בשני החריצים באותו זמן, ומודל זה מוביל לפרשנות נוחה יותר של הניסוי הזה.

עקרון האי-ודאות

בכל פעם שמודדים את המיקום או המהירות של חלקיק ברגע כלשהו, ישנן אי-ודאויות ניסיוניות במדידות. על פי המכניקה הקלאסית, אפשר לבצע מדידות כאלה עם אי-ודאות קטנה באופן שרירותי. התיאוריה הקוונטית מנבאת, עם זאת, שמבחינה יסודית בלתי אפשרי לבצע מדידות בו-זמניות של המיקום והתנע של חלקיק בדיוק אינסופי. בשנת 1927, ורנר הייזנברג (1901–1976) הציג רעיון זה, שנקרא כעת עקרון האי-ודאות של הייזנברג:

משפט: עקרון האי-ודאות של הייזנברג

אם מדידה של המיקום של חלקיק נעשית עם אי-ודאות ומדידה בו-זמנית של רכיב ה- של התנע שלו נעשית עם אי-ודאות , המכפלה של שתי האי-ודאויות לא יכולה להיות קטנה יותר מ-:

כלומר, מבחינה פיזיקלית בלתי אפשרי למדוד בו-זמנית את המיקום המדויק והתנע המדויק של חלקיק. הייזנברג הקפיד להדגיש שהאי-ודאויות הבלתי נמנעות ו- אינן נובעות מאי-שלמויות במכשירי מדידה מעשיים. במקום זאת, האי-ודאויות נובעות מהמבנה הקוונטי של החומר.

כדי להבין את עקרון האי-ודאות, דמיינו שלחלקיק יש אורך גל יחיד הידוע בדיוק. על פי יחס דה ברויי, , לכן נדע שהתנע הוא בדיוק . במציאות, גל באורך גל יחיד יתקיים בכל המרחב. כל אזור לאורך הגל הזה זהה לכל אזור אחר (איור 2.1). נניח שאנו שואלים, איפה החלקיק שהגל הזה מייצג? לא ניתן לזהות מיקום מיוחד במרחב לאורך הגל עם החלקיק; כל הנקודות לאורך הגל זהות. לכן, יש לנו אי-ודאות אינסופית במיקום החלקיק, ואיננו יודעים דבר על מיקומו. ידע מושלם על התנע של החלקיק עלה לנו את כל המידע על מיקומו.

בהשוואה, שקלו כעת חלקיק שהתנע שלו אינו ודאי כך שיש לו טווח של ערכי תנע אפשריים. על פי יחס דה ברויי, התוצאה היא טווח של אורכי גל. לכן, החלקיק אינו מיוצג על ידי אורך גל יחיד, אלא בשילוב של אורכי גל בטווח זה. השילוב הזה יוצר צרור גלים. אם תתבקשו לקבוע את מיקום החלקיק, תוכלו רק לומר שהוא איפשהו באזור המוגדר על ידי צרור הגלים מכיוון שיש הבדל ברור בין אזור זה לשאר המרחב. לכן, על ידי אובדן חלק מהמידע על התנע של החלקיק, קיבלנו מידע על מיקומו. אם הייתם מאבדים את כל המידע על התנע, הייתם מחברים גלים של כל אורכי הגל האפשריים, וכתוצאה מכך צרור גלים באורך אפס. לכן, אם אתם לא יודעים דבר על התנע, אתם יודעים בדיוק איפה החלקיק נמצא.

הצורה המתמטית של עקרון האי-ודאות קובעת שמכפלת האי-ודאויות במיקום ובתנע תמיד גדולה מערך מינימלי מסוים.

צורה אחרת של עקרון האי-ודאות יכולה להיווצר על ידי דמיון שהציר האופקי באיור איור 2.2 הוא זמן במקום מיקום מרחבי , מכיוון שגל תלוי גם ב- וגם ב-. כעת, נוכל לטעון את אותם טיעונים בתחום הזמן שנטענו לגבי ידע של אורך גל ומיקום. המשתנים המתאימים יהיו תדירות וזמן. מכיוון שתדירות קשורה לאנרגיה של החלקיק על ידי , עקרון האי-ודאות בצורה זו הוא:

הצורה של עקרון האי-ודאות הנתונה במשוואה (SJ39.24) מציעה שחיסכון באנרגיה יכול להיראות כמופר בכמות כל עוד זה רק לפרק זמן קצר העולה בקנה אחד עם אותה משוואה.

דוגמה: איתור אלקטרון

מהירותו של אלקטרון נמדדת כ- לדיוק של . מצאו את האי-ודאות המינימלית בקביעת המיקום של האלקטרון הזה.

פתרון:

הערך הנתון לדיוק מהירות האלקטרון יכול להיות מפורש כאי-ודאות בתנעו. אי-ודאות זו מתאימה לאי-ודאות מינימלית במיקום האלקטרון דרך עקרון האי-ודאות.

נניח שהאלקטרון נע לאורך ציר ה- ונמצא את האי-ודאות ב-, כאשר מייצג את הדיוק של מדידת המהירות שלו:

פותרים את משוואה (SJ39.23) עבור האי-ודאות במיקום האלקטרון ומציבים ערכים מספריים:

דוגמה: רוחב הפס של פליטות אטומיות

לאטומים יש רמות אנרגיה מקוונטות דומות לאלה של מתנדי פלאנק, אם כי רמות האנרגיה של אטום בדרך כלל אינן מרווחות באופן שווה. כאשר אטום עושה מעבר בין מצבים המופרדים באנרגיה ב-, אנרגיה נפלטת בצורת פוטון בתדירות . למרות שאטום מעורר יכול לקרון בכל זמן מ- עד , מרווח הזמן הממוצע אחרי עירור שבמהלכו אטום קורן נקרא זמן החיים . אם , השתמשו בעקרון האי-ודאות כדי לחשב את רוחב הקו המיוצר על ידי זמן חיים סופי זה.

פתרון:

זמן החיים הנתון למצב המעורר יכול להיות מפורש כאי-ודאות בזמן שבו המעבר מתרחש. אי-ודאות זו מתאימה לאי-ודאות מינימלית בתדירות הפוטון הנקרן דרך עקרון האי-ודאות.

משתמשים במשוואה (SJ39.5) כדי לקשר את האי-ודאות בתדירות הפוטון לאי-ודאות באנרגיה שלו:

משתמשים במשוואה (SJ39.24) כדי להציב עבור האי-ודאות באנרגיה הפוטון, ונותנים את הערך המינימלי של :

מציבים עבור זמן החיים של המצב המעורר:

→ קודם: PHY3_001הבא: PHY3_003 ←