PHY3_003 מכניקה קוונטית א

→ קודם: PHY3_002הבא: PHY3_004 ←

פונקציית הגל

בפרק הקודם, הצגנו כמה רעיונות חדשים ומוזרים. הגענו למסקנה על בסיס עדויות ניסיוניות שגם חומר וגם קרינה אלקטרומגנטית ממודלים לעתים הכי טוב כחלקיקים ולעתים כגלים, תלוי בתופעה שנצפית. חקרנו את הרעיון של צרור גלים כדי לעזור לנו להבין את הטבע הדואלי הזה. אנו יכולים לשפר את ההבנה שלנו של פיזיקה קוונטית עוד יותר על ידי יצירת קשר נוסף בין חלקיקים לגלים באמצעות הרעיון של הסתברות.

נתחיל בדיון בקרינה אלקטרומגנטית באמצעות מודל החלקיק. ההסתברות ליחידת נפח למציאת פוטון באזור נתון במרחב ברגע זמן נתון פרופורציונלית למספר הפוטונים ליחידת נפח באותו זמן:

מספר הפוטונים ליחידת נפח פרופורציונלי לעוצמת הקרינה:

כעת, בואו ניצור קשר בין מודל החלקיק למודל הגל על ידי העובדה שעוצמת הקרינה האלקטרומגנטית פרופורציונלית לריבוע משרעת השדה החשמלי עבור הגל האלקטרומגנטי:

השוואת ההתחלה והסוף של סדרת הפרופורציונליות הזו נותנת:

לכן, עבור קרינה אלקטרומגנטית, ההסתברות ליחידת נפח למציאת חלקיק הקשור לקרינה זו (הפוטון) פרופורציונלית לריבוע המשרעת של הגל האלקטרומגנטי המשויך.

בהכרה בדואליות גל-חלקיק הן של קרינה אלקטרומגנטית והן של חומר, נוכל לשער שישנה בפרופורציונליות מקבילה עבור חלקיק חומרי: ההסתברות ליחידת נפח למציאת החלקיק פרופורציונלית לריבוע המשרעת של גל המייצג את החלקיק.

בפרק הקודם, למדנו שיש גל דה ברויי הקשור לכל חלקיק. המשרעת של גל דה ברויי הקשור לחלקיק אינה כמות הניתנת למדידה מכיוון שפונקציית הגל המייצגת חלקיק היא בדרך כלל פונקציה מרוכבת כפי שנדון להלן. לעומת זאת, השדה החשמלי עבור גל אלקטרומגנטי הוא פונקציה ממשית.

האנלוג החומרי למשוואה (SJ40.1) קושר את ריבוע המשרעת של הגל להסתברות ליחידת נפח למציאת החלקיק. לכן, המשרעת של הגל הקשור לחלקיק נקראת משרעת ההסתברות, או פונקציית הגל, ויש לה את הסמל . עבור חלקיקים חומריים, תמלא את התפקיד של במשוואה (SJ40.1).

באופן כללי, פונקציית הגל קשורה למערכת ותלויה במיקומים של כל החלקיקים במערכת ובזמן; לכן, ניתן לכתוב אותה כ-, כאשר הוא וקטור המיקום של החלקיק ה- במערכת.

לעתים קרובות, אנו מעוניינים בהתנהגות המערכת הקשורה לשינויים רק באחד מחלקיקיה, שאותו נוכל לזהות כחלקיק ה-. עבור מערכות רבות, פונקציית הגל ניתנת להפרדה מתמטית במרחב ובזמן וניתן לכתוב אותה כמכפלה של פונקציית מרחב עבור החלקיק ופונקציית זמן מרוכבת:

כאשר היא התדירות הזוויתית של פונקציית הגל ו-. התדירות קשורה לאנרגיה של החלקיק דרך יחס פלאנק (SJ39.5): .

הערה: מספרים מרוכבים

איור 3.1: הצורה הסטנדרטית של מספר מרוכב היא . הסימון שווה לצורה הסטנדרטית כדלהלן:

לכן, הסימון במשוואה (SJ40.2) שווה ל-.

עבור כל מערכת שבה האנרגיה הפוטנציאלית אינה תלויה בזמן ותלויה רק במיקומי החלקיקים במערכת, המידע החשוב על המערכת כלול בחלק המרחבי של פונקציית הגל. חלק הזמן הוא פשוט הגורם . לכן, הבנה של היא ההיבט הקריטי של בעיה נתונה.

פונקציית הגל היא לעתים קרובות בעלת ערך מרוכב. הריבוע המוחלט , כאשר הוא הצמוד המרוכב של , הוא תמיד ממשי וחיובי ופרופורציונלי להסתברות ליחידת נפח למציאת חלקיק בנקודה נתונה ברגע מסוים.

הגדרה: פונקציית הגל

איור 3.2: פונקציית הגל מכילה בתוכה את כל המידע הניתן לדעת על החלקיק. למרות ש- אינה ניתנת למדידה, אנו יכולים למדוד את הכמות הממשית , שניתן לפרש אותה כדלהלן.

אם מייצגת חלקיק יחיד, אז - הנקראת צפיפות ההסתברות - היא ההסתברות היחסית ליחידת נפח שהחלקיק יימצא בכל נקודה נתונה בנפח. פרשנות זו יכולה להיאמר גם באופן הבא. אם הוא אלמנט נפח קטן המקיף נקודה כלשהי, ההסתברות למציאת החלקיק באותו אלמנט נפח היא:

הפרשנות ההסתברותית הזו של פונקציית הגל הוצעה לראשונה על ידי מקס בורן (1882–1970) בשנת 1928.

בשנת 1926, ארווין שרדינגר הציע משוואת גל המתארת את האופן שבו פונקציית הגל משתנה במרחב ובזמן. משוואת הגל של שרדינגר, מייצגת רכיב מרכזי בתיאוריה של המכניקה הקוונטית.

בפרק הקודם, מצאנו שמשוואת דה ברויי קושרת את התנע של חלקיק לאורך הגל שלו דרך היחס המתואר ע”י משוואה (SJ39.15): . אם לחלקיק חופשי אידיאלי יש תנע ידוע במדויק , פונקציית הגל שלו היא גל סינוסואידי ארוך לאין סוף באורך גל ולחלקיק יש הסתברות שווה להיות בכל נקודה לאורך ציר ה-.

פונקציית הגל עבור חלקיק חופשי כזה הנע לאורך ציר ה- יכולה להיכתב כ:

כאשר הוא משרעת קבועה ו- הוא מספר הגל הזוויתי של הגל המייצג את החלקיק.

מסקנה: קשר לפיזיקה קלאסית

איור 3.3: המושגים של מכניקה קוונטית, מוזרים ככל שהם לפעמים, התפתחו מרעיונות קלאסיים. למעשה, כאשר הטכניקות של מכניקה קוונטית מיושמות על מערכות מקרוסקופיות, התוצאות זהות בעיקרן לאלה של פיזיקה קלאסית. התערבות זו של שתי הגישות מתרחשת כאשר אורך הגל של דה ברויי קטן בהשוואה למימדי המערכת. המצב דומה להסכמה בין מכניקה יחסותית למכניקה קלאסית כאשר .

פונקציות גל חד-מימדיות וערכי ציפייה

סעיף זה דן רק במערכות חד-מימדיות, שבהן החלקיק חייב להיות ממוקם לאורך ציר ה-, כך שההסתברות במשוואה (SJ40.3) הופכת להיות . ההסתברות שהחלקיק יימצא במרווח האינפיניטסימלי סביב הנקודה היא:

למרות שאי אפשר לחשב את מיקום החלקיק בוודאות מלאה, אפשר דרך לחשב את ההסתברות לצפות בו באזור המקיף נקודה נתונה . ההסתברות למציאת החלקיק במרווח השרירותי היא:

ההסתברות היא השטח מתחת לעקומה של כנגד בין הנקודות ו-, כפי שמוצג באיור.

מבחינה ניסיונית, יש הסתברות סופית למציאת חלקיק במרווח ליד נקודה כלשהי ברגע כלשהו. הערך של אותה הסתברות חייב להיות בין הגבולות ו-. לדוגמה, אם ההסתברות היא , יש סיכוי של למציאת החלקיק במרווח.

מכיוון שהחלקיק חייב להיות איפשהו לאורך ציר ה-, סכום ההסתברויות על פני כל הערכים של חייב להיות :

כל פונקציית גל המקיימת את משוואה (SJ40.7) נקראת מנורמלת. נורמליזציה היא פשוט הצהרה שהחלקיק קיים בנקודה כלשהי במרחב.

לאחר שפונקציית הגל עבור חלקיק ידועה, אפשר לחשב את המיקום הממוצע שבו הייתם מצפים למצוא את החלקיק לאחר מדידות רבות. המיקום הממוצע הזה נקרא ה**תּוֹחֶלֶת (expectation value)** של ומוגדר על ידי המשוואה:

(סוגריים מעוגלים, , משמשים לציון תוחלת.)

יתר על כן, ניתן למצוא את התוחלת של כל פונקציה הקשורה לחלקיק באמצעות המשוואה הבאה:

הערה: תוחלת

איור 3.4: ערכי ציפייה אנלוגיים ל”ממוצעים משוקללים”, שבהם כל ערך אפשרי של פונקציה מוכפל בהסתברות להתרחשות של אותו ערך לפני סיכום על פני כל הערכים האפשריים. אנו כותבים את ערך הציפייה כ- במקום מכיוון ש- עשוי להיות מיוצג על ידי אופרטור (כמו נגזרת) במקום פונקציה כפלית פשוטה בטיפולים מתקדמים יותר של מכניקה קוונטית.

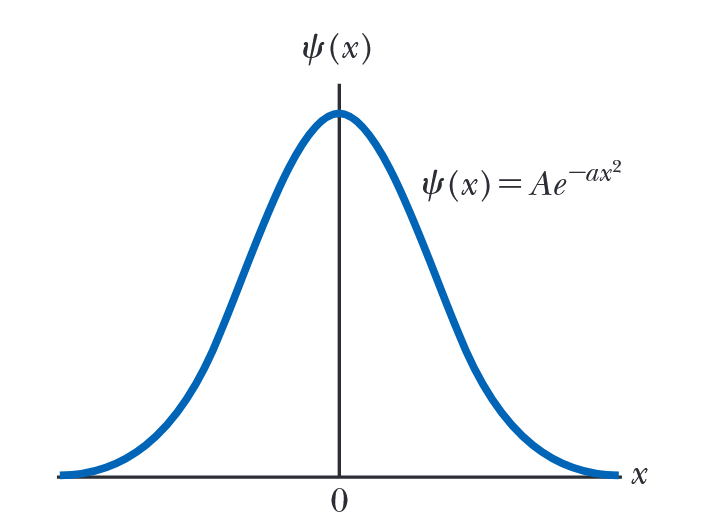
איור 3.5: פונקציית גל סימטרית של חלקיק, הנתונה ע”י . (Serway et al., 2019).

דוגמה: פונקציית גל עבור חלקיק

איור 3.6: נתון חלקיק שפונקציית הגל שלו נתונה על ידי:

מה הערך של אם פונקציית הגל הזו מנורמלת?

פתרון:

החלקיק אינו חלקיק חופשי מכיוון שפונקציית הגל אינה פונקציה סינוסואידית. החלקיק מוגבל להישאר קרוב ל- בכל עת. דוגמאות למערכות כאלה הן בלוק על קפיץ, גולה בתחתית קערה, וכדור של מטוטלת פשוטה. בעוד שפונקציות גל רבות הן פונקציות מרוכבות, זו במקרה ממשית, כך ש-.

ניישם את תנאי הנורמליזציה, משוואה (SJ40.7), על פונקציית הגל:

נביע את האינטגרל כסכום של שני אינטגרלים:

נשנה את משתנה האינטגרציה מ- ל- באינטגרל השני:

נהפוך את סדר הגבולות, מה שמכניס סימן שלילי:

נציב את הביטוי הזה עבור האינטגרל השני:

נחשב את האינטגרל:

נציב תוצאה זו ונפתור עבור :

דוגמה:

מה ערך הציפייה של עבור החלקיק מהדוגמה הקודמת?

פתרון:

נחשב את ערך הציפייה באמצעות משוואה (SJ40.8):

נביע את האינטגרל כסכום של שני אינטגרלים:

נשנה את משתנה האינטגרציה מ- ל- באינטגרל השני:

נהפוך את סדר הגבולות:

נציב בחזרה בחישוב התוחלת:

בהתחשב בסימטריה של פונקציית הגל סביב , לא מפתיע שהמיקום הממוצע של החלקיק הוא ב-.

מודל אנליטי: חלקיק קוונטי תחת תנאי שפה

בפיזיקה 2, חקרנו את התוצאות של הטלת תנאי שפה על גלים, הן על מיתרים והן בעמודי אוויר. מצאנו שהטלת תנאי שפה הביאה לתדירויות מקוונטות שבהן המערכת יכולה לנדוד. בואו נסתכל על התוצאות של הטלת תנאי שפה על חלקיקים קוונטיים. החלקיק החופשי שנדון בסעיף הקודם אינו כפוף לתנאי שפה; הוא יכול להיות בכל מקום במרחב. החלקיק בדוגמה הקודמת אינו חלקיק חופשי. איור 3.2 מראה שהחלקיק מוגבל תמיד למיקומים ליד . בסעיף זה, נחקור את ההשפעות של הטלת תנאי השפה הפשוטים ביותר האפשריים על חלקיק.

חלקיק בקופסה

דמיינו שהחלקיק החופשי מהסעיף הקודם נע לאורך ציר ה- ואנו פתאום שמים קופסה סביבו, כך שהוא מוגבל לחזור בצורה אלסטית מהקירות של הקופסה, ולנוע הלוך ושוב לאורך ציר ה-. זוהי בעיה אמיתית בפיזיקה, הנקראת בעיית החלקיק-בקופסה (למרות שה”קופסה” היא חד-מימדית!).

מנקודת מבט קלאסית, אם חלקיק מקפץ אלסטית הלוך ושוב לאורך ציר ה- בין שני קירות בלתי חדירים המופרדים במרחק כמו בייצוג הציורי באיור 3.2, ניתן למדל אותו כחלקיק תחת מהירות קבועה. אם מהירות החלקיק היא , גודל התנע שלו נשאר קבוע וכך גם האנרגיה הקינטית שלו. הפיזיקה הקלאסית אינה מטילה הגבלות על הערכים של התנע והאנרגיה של החלקיק.

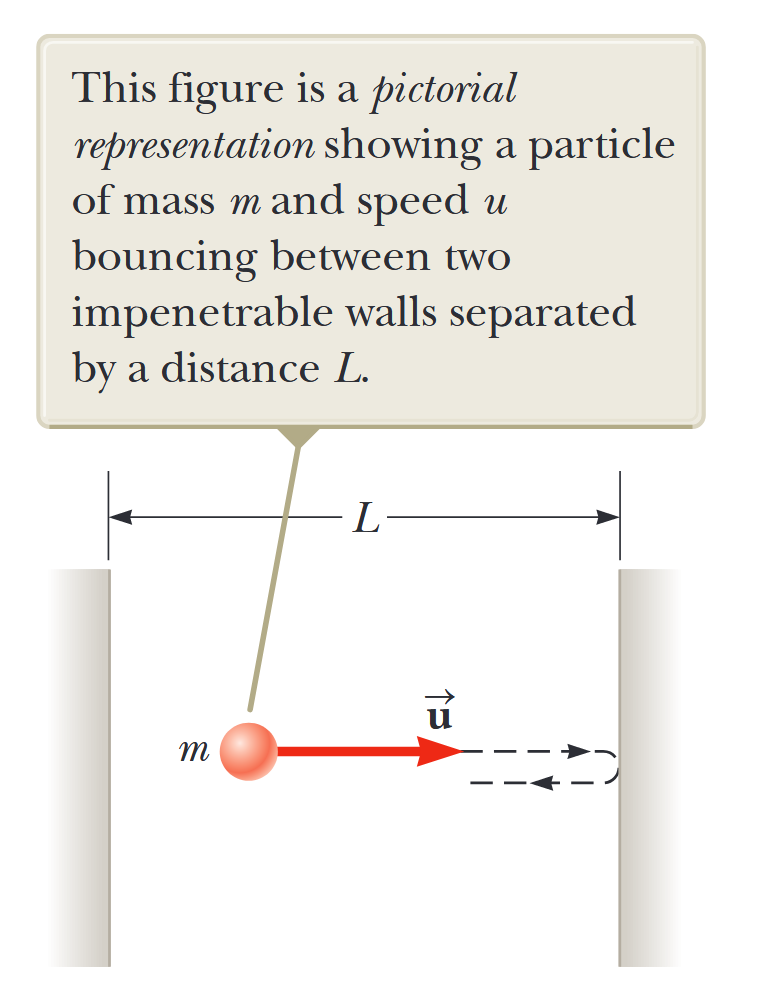
ייצוג ציורי המראה חלקיק בעל מסה ומהירות המקפץ בין שני קירות בלתי חדירים המופרדים במרחק . (Serway et al., 2019).

הגישה המכני-קוונטית לבעיה זו שונה לחלוטין ודורשת שנמצא את פונקציית הגל המתאימה העקבית עם תנאי המערכת. מכיוון שהקירות בלתי חדירים, יש הסתברות אפס למציאת החלקיק מחוץ לקופסה, ולכן פונקציית הגל חייבת להיות אפס עבור ו-. כדי להיות פונקציה הגיונית מתמטית, חייבת להיות רציפה במרחב. אסור שיהיו קפיצות לא רציפות בערך של פונקציית הגל בשום נקודה. לכן, אם היא אפס מחוץ לקירות, היא חייבת להיות אפס גם בקירות; כלומר, ו-. רק פונקציות הגל המקיימות את תנאי השפה הללו מותרות.

איור 3.3, ייצוג גרפי של בעיית החלקיק-בקופסה, מראה את האנרגיה הפוטנציאלית של מערכת החלקיק-סביבה כפונקציה של מיקום החלקיק. כל עוד החלקיק נמצא בתוך הקופסה, האנרגיה הפוטנציאלית של המערכת אינה תלויה במיקום החלקיק ונוכל לבחור שהערך הקבוע שלה יהיה אפס. מחוץ לקופסה, עלינו להבטיח שפונקציית הגל תהיה אפס. נוכל לעשות זאת על ידי הגדרת האנרגיה הפוטנציאלית של המערכת כגדולה לאין סוף אם החלקיק היה מחוץ לקופסה. לכן, הדרך היחידה שבה חלקיק יכול להיות מחוץ לקופסה היא אם למערכת יש כמות אינסופית של אנרגיה, מה שבלתי אפשרי.

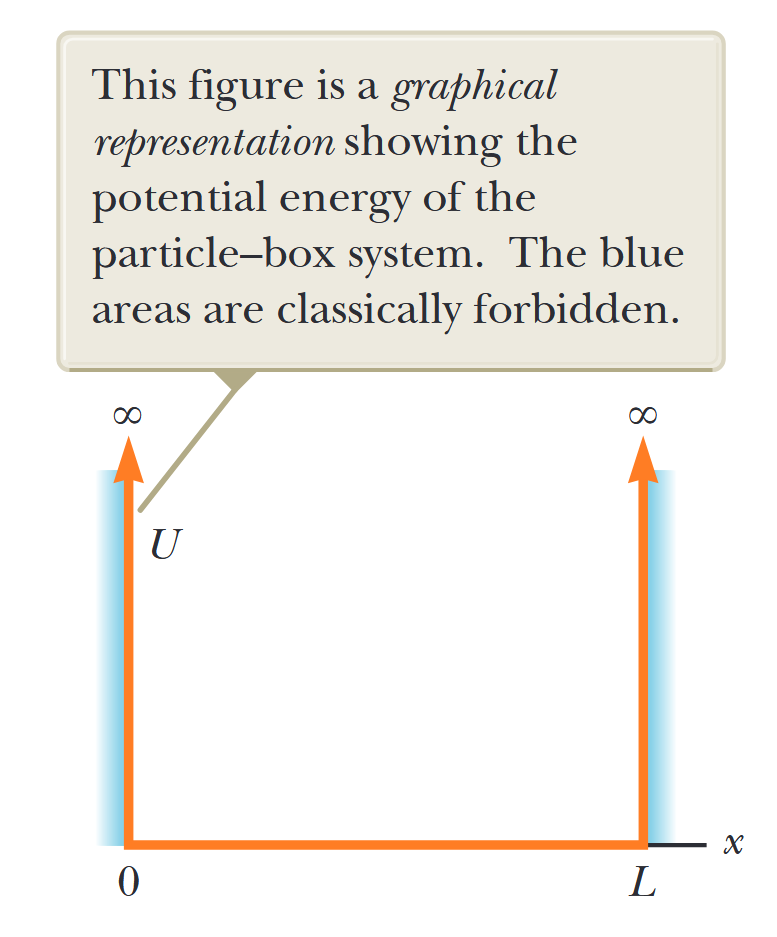
ייצוג גרפי המראה את האנרגיה הפוטנציאלית של מערכת החלקיק-קופסה. האזורים הכחולים אסורים קלאסית. (Serway et al., 2019).

פונקציית הגל עבור חלקיק בקופסה יכולה להתבטא כפונקציה סינוסואידית ממשית:

כאשר הוא אורך הגל של דה ברויי הקשור לחלקיק. פונקציית הגל הזו חייבת לקיים את תנאי השפה בקירות. תנאי השפה מתקיים כבר מכיוון שפונקציית הסינוס היא אפס כאשר . תנאי השפה נותן:

מה שיכול להיות נכון רק אם:

כאשר . לכן, רק אורכי גל מסוימים עבור החלקיק מותרים! כל אחד מאורכי הגל המותרים מתאים למצב קוונטי של המערכת, ו- הוא המספר הקוונטי.

שילוב משוואה (SJ40.11) במשוואה (SJ40.10) נותן:

נורמליזציה של פונקציית הגל הזו מראה ש-. לכן, פונקציית הגל המנורמלת עבור החלקיק בקופסה היא:

איור 3.4 ו-איור 3.5 מוצגים ייצוגים גרפיים של כנגד ושל כנגד עבור של החלקיק בקופסה. למרות שפונקציית גל כללית יכולה להיות בעלת ערכים חיוביים ושליליים, תמיד חיובית. מכיוון ש- מייצגת צפיפות הסתברות, ערך שלילי עבור יהיה חסר משמעות.

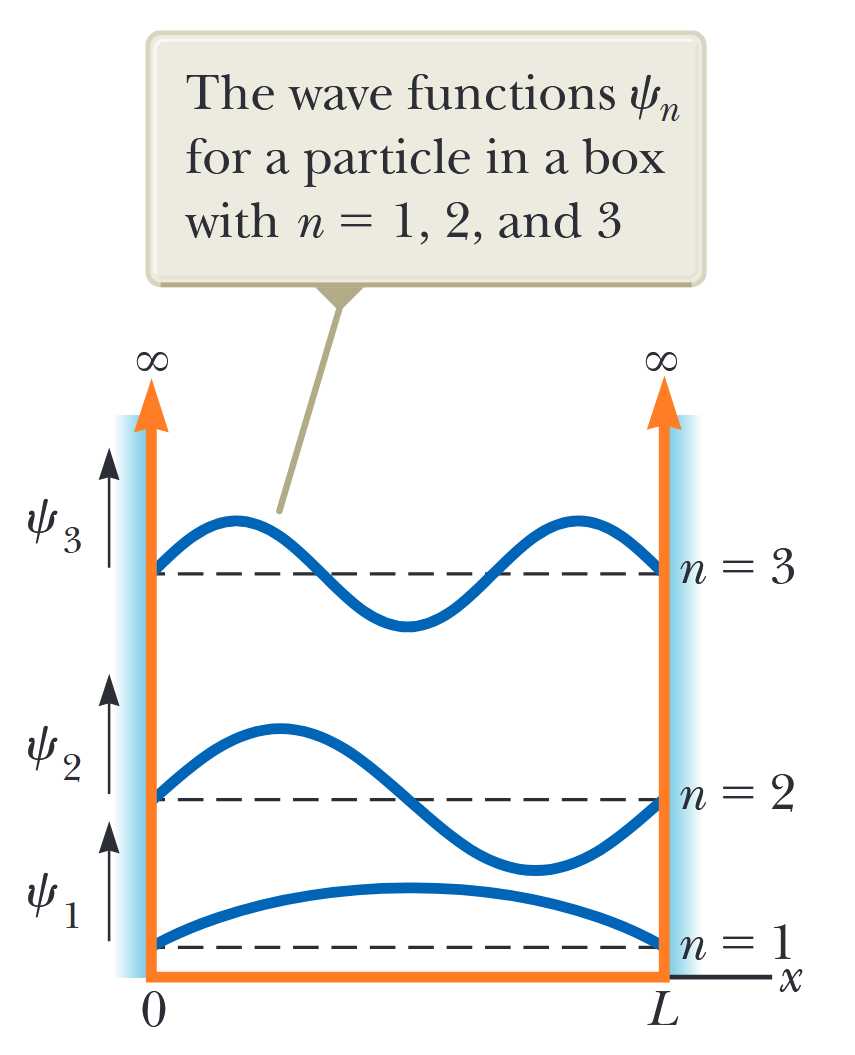
פונקציות הגל עבור חלקיק בקופסה עם . (Serway et al., 2019).

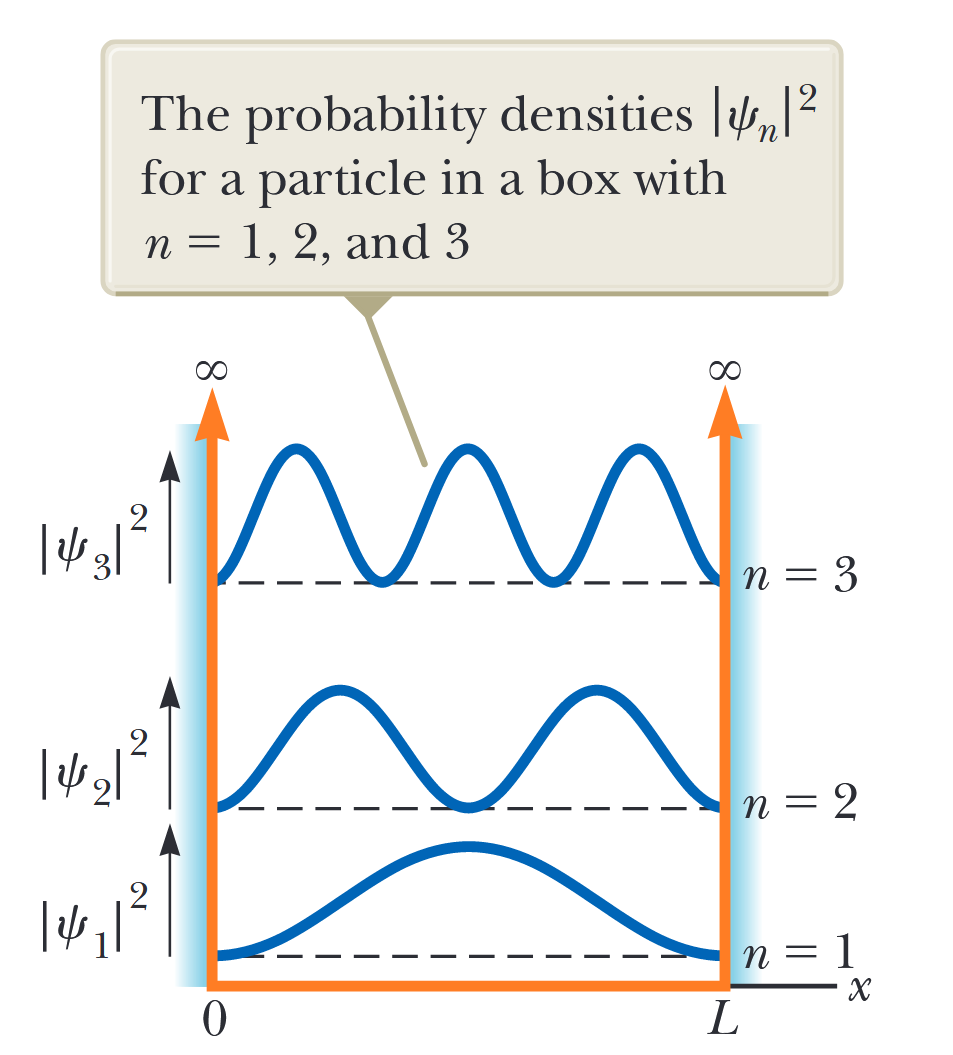
צפיפויות ההסתברות עבור חלקיק בקופסה עם . (Serway et al., 2019).

מה שאנו דנים בו כאן עשוי להתחיל להישמע מוכר לכם — הרבה ממה שאנו עושים כאן דומה מאוד לגלים עומדים על מיתרים, כפי שנראה בפיזיקה 2.

בדיקה נוספת של איור 3.5 מראה ש- היא אפס בגבולות, כלומר היא מקיימת את תנאי השפה שלנו. בנוסף, היא אפס בנקודות אחרות, תלוי בערך של . עבור , ב-; עבור , ב- וב-. מספר נקודות האפס גדל באחד בכל פעם שהמספר הקוונטי גדל באחד.

מכיוון שאורכי הגל של החלקיק מוגבלים על ידי התנאי , גודל התנע של החלקיק מוגבל גם הוא לערכים ספציפיים, שניתן למצוא מהביטוי לאורך הגל של דה ברויי, משוואה (SJ39.15):

בחרנו שהאנרגיה הפוטנציאלית של המערכת תהיה אפס כאשר החלקיק נמצא בתוך הקופסה. לכן, האנרגיה של המערכת היא פשוט האנרגיה הקינטית של החלקיק והערכים המותרים נתונים על ידי:

ביטוי זה מראה שהאנרגיה של החלקיק מקוונטת. האנרגיה הנמוכה ביותר המותרת מתאימה למצב היסוד, שהוא מצב האנרגיה הנמוך ביותר עבור כל מערכת. עבור החלקיק בקופסה, מצב היסוד מתאים ל-, שעבורו . מכיוון ש-, המצבים המעוררים המתאימים ל- בעלי אנרגיות הנתונות על ידי .

איור 3.6 הוא תרשים רמות אנרגיה המתאר את ערכי האנרגיה של המצבים המותרים. מכיוון שהאנרגיה הנמוכה ביותר של החלקיק בקופסה אינה אפס, אז, על פי המכניקה הקוונטית, החלקיק לעולם אינו יכול להיות במנוחה! האנרגיה הקטנה ביותר שיכולה להיות לו, המתאימה ל-, נקראת אנרגיית מצב היסוד. תוצאה זו סותרת את השקפת העולם הקלאסית, שבה הוא מצב מקובל, כמו גם כל הערכים החיוביים של .

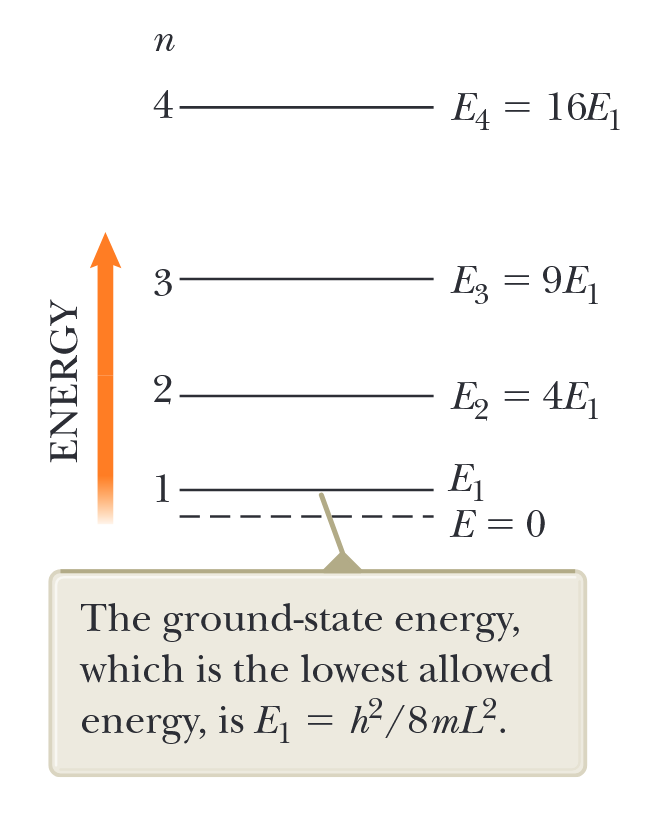
תרשים רמות אנרגיה עבור חלקיק המוגבל לקופסה חד-מימדית באורך . אנרגיית מצב היסוד, שהיא האנרגיה הנמוכה ביותר המותרת, היא . (Serway et al., 2019).

דוגמה: חלקיקים מיקרוסקופיים ומקרוסקופיים בקופסאות

אלקטרון מוגבל בין שני קירות בלתי חדירים הרחוקים ננומטר זה מזה. מצאו את רמות האנרגיה עבור המצבים .

פתרון:

נשתמש במשוואה (SJ40.14) עבור מצב :

באמצעות , נמצא את האנרגיות של המצבים ו-:

דוגמה: מהירות האלקטרון

מצאו את המהירות של האלקטרון במצב מהדוגמה הקודמת.

פתרון:

נפתור את הביטוי הקלאסי לאנרגיה קינטית עבור מהירות החלקיק:

נכיר שהאנרגיה הקינטית של החלקיק שווה לאנרגיה המערכת ונציב במקום :

נציב ערכים מספריים מהחלק הקודם:

פשוט הצבת האלקטרון בקופסה מביאה למהירות מינימלית של האלקטרון השווה ל- ממהירות האור!

דוגמה: כדור בייסבול מקרוסקופי

כדור בייסבול במסה ק”ג מוגבל בין שני קירות קשיחים של אצטדיון שניתן לדגמן כקופסה באורך מ’. חשבו את המהירות המינימלית של כדור הבייסבול.

פתרון:

נשתמש במשוואה (SJ40.14) עבור מצב :

נשתמש בביטוי למהירות:

מהירות זו קטנה כל כך שהעצם יכול להיחשב כנמצא במנוחה, מה שאפשר לצפות עבור המהירות המינימלית של עצם מקרוסקופי.

תנאי שפה על חלקיקים באופן כללי

הדיון בחלקיק בקופסה בעל דמיון מסוים לדיון על גלים עומדים על מיתרים:

• מכיוון שקצוות המיתר חייבים להיות צמתים, פונקציות הגל עבור גלים מותרים חייבות להיות אפס בגבולות המיתר. מכיוון שהחלקיק בקופסה אינו יכול להתקיים מחוץ לקופסה, פונקציות הגל המותרות עבור החלקיק חייבות להיות אפס בגבולות.

• תנאי השפה על גלי המיתר מובילים לאורכי גל ותדירויות מקוונטות של הגלים. תנאי השפה על פונקציית הגל עבור החלקיק בקופסה מובילים לאורכי גל ותדירויות מקוונטות של החלקיק.

במכניקה קוונטית, נפוץ מאוד שחלקיקים כפופים לתנאי שפה. לכן אנו מציגים מודל אנליטי חדש, החלקיק הקוונטי תחת תנאי שפה. במובנים רבים, מודל זה דומה למודל הגלים תחת תנאי שפה.

המודל החלקיק הקוונטי תחת תנאי שפה שונה במובנים מסוימים ממודל הגלים תחת תנאי שפה:

• ברוב המקרים של חלקיקים קוונטיים מעבר לחלקיק בקופסה, פונקציית הגל אינה פונקציה סינוסואידית פשוטה כמו פונקציית הגל עבור גלים על מיתרים. יתר על כן, פונקציית הגל עבור חלקיק קוונטי עשויה להיות פונקציה מרוכבת.

• עבור חלקיק קוונטי, התדירות קשורה לאנרגיה דרך , כך שהתדירויות המקוונטות מובילות לאנרגיות מקוונטות.

• ייתכן שאין צמתים נייחים הקשורים לפונקציית הגל של חלקיק קוונטי תחת תנאי שפה. מערכות מורכבות יותר מהחלקיק בקופסה בעלות פונקציות גל מורכבות יותר, וכמה תנאי שפה עלולים לא להוביל לאפסים של פונקציית הגל בנקודות קבועות.

באופן כללי, אינטראקציה של חלקיק קוונטי עם סביבתו מייצגת תנאי שפה אחד או יותר, ואם האינטראקציה מגבילה את החלקיק לאזור סופי במרחב, היא מביאה לקוונטיזציה של האנרגיה של המערכת.

תנאי שפה על פונקציות גל קוונטיות קשורים לקואורדינטות המתארות את הבעיה. עבור החלקיק בקופסה, פונקציית הגל חייבת להיות אפס בקצות הקופסה. במקרה של מערכת תלת-מימדית כמו אטום המימן שנדון בהמשך, הבעיה מוצגת בצורה הטובה ביותר בקואורדינטות כדוריות. קואורדינטות אלה, מורכבות מקואורדינטה רדיאלית ושתי קואורדינטות זוויתיות. היצירה של פונקציית הגל והיישום של תנאי השפה עבור אטום המימן הם מעבר לטווח של ספר זה. נבחן, עם זאת, את ההתנהגות של חלק מפונקציות הגל של אטום המימן בהמשך.

מודל אנליטי: חלקיק קוונטי תחת תנאי שפה

דמיינו חלקיק המתואר על ידי פיזיקה קוונטית הכפוף לתנאי שפה אחד או יותר. אם החלקיק מוגבל לאזור סופי במרחב על ידי תנאי השפה, האנרגיה של המערכת מקוונטת. הקשור לכל אנרגיה מקוונטת הוא מצב קוונטי המאופיין על ידי פונקציית גל ומספר קוונטי.

דוגמאות:

• אלקטרון בנקודה קוונטית אינו יכול לברוח, ממקוונט את האנרגיות של האלקטרון.
• אלקטרון באטום מימן מוגבל להישאר ליד גרעין האטום, ממקוונט את האנרגיות של האטום.
• שני אטומים קשורים ליצירת מולקולה דו-אטומית, ממקוונטים את האנרגיות של רטט וסיבוב של המולקולה.
• פרוטון לכוד בגרעין, ממקוונט את רמות האנרגיה שלו.

משוואת שרדינגר

בפיזיקה 2, דנו במשוואת גל ליניארית עבור גלים מכניים, הנובעת מחוקי ניוטון. דנו גם במשוואת גל ליניארית עבור קרינה אלקטרומגנטית הנובעת ממשוואות מקסוול. הגלים הקשורים לחלקיקים מקיימים גם הם משוואת גל. משוואת הגל עבור חלקיקים חומריים שונה מזו הקשורה לפוטונים מכיוון שלחלקיקים חומריים יש אנרגיית מנוחה שאינה אפס. משוואת הגל המתאימה פותחה על ידי שרדינגר בשנת 1926. פיתוח זה הוביל לגישה סטנדרטית לניתוח התנהגות של מערכת קוונטית. הגישה היא לקבוע פתרון למשוואת שרדינגר ואז להחיל את תנאי השפה המתאימים על הפתרון. תהליך זה מניב את פונקציות הגל ורמות האנרגיה המותרות של המערכת הנחקרת. טיפול נכון בפונקציית הגל מאפשר אז לחשב את כל המאפיינים הניתנים למדידה של המערכת.

משוואת שרדינגר כפי שהיא חלה על חלקיק במסה המוגבל לתנועה לאורך ציר ה- והמקיים אינטראקציה עם סביבתו דרך פונקציית אנרגיה פוטנציאלית היא:

כאשר הוא קבוע השווה לאנרגיה הכוללת של המערכת (החלקיק וסביבתו), ו-. מכיוון שמשוואה זו אינה תלויה בזמן, היא נקראת בדרך כלל משוואת שרדינגר הבלתי-תלויה בזמן.

מסקנה: עקרון שימור האנרגיה

משוואת שרדינגר עקבית עם עקרון שימור האנרגיה המכנית עבור מערכת מבודדת ללא כוחות לא-שמרניים הפועלים עליה. האיבר הראשון במשוואת שרדינגר הוא פשוט האנרגיה הקינטית של החלקיק כפול פונקציית הגל. לכן, משוואה (SJ40.15) מציינת שהאנרגיה הכוללת של המערכת היא סכום האנרגיה הקינטית והאנרגיה הפוטנציאלית ושהאנרגיה הכוללת היא קבוע: .

עקרונית, אם פונקציית האנרגיה הפוטנציאלית עבור מערכת ידועה, ניתן לפתור את משוואה (SJ40.15) ולקבל את פונקציות הגל והאנרגיות עבור המצבים המותרים של המערכת. בנוסף, במקרים רבים, פונקציית הגל חייבת לקיים תנאי שפה. לכן, לאחר שיש לנו פתרון ראשוני למשוואת שרדינגר, אנו מטילים את התנאים הבאים כדי למצוא את הפתרון המדויק והאנרגיות המותרות:

• חייבת להיות ניתנת לנורמליזציה. כלומר, משוואה (SJ40.7) חייבת להיות מקוימת.
• חייבת לשאוף ל- כאשר ולהישאר סופית כאשר .
• חייבת להיות רציפה ב- ובעלת ערך יחיד בכל מקום; פתרונות למשוואה (SJ40.15) באזורים שונים חייבים להתחבר בצורה חלקה בגבולות בין האזורים.
• חייבת להיות סופית, רציפה ובעלת ערך יחיד בכל מקום עבור ערכים סופיים של . אם לא הייתה רציפה, לא היינו יכולים לחשב את הנגזרת השנייה במשוואה (SJ40.15) בנקודת חוסר הרציפות.

המשימה של פתרון משוואת שרדינגר עלולה להיות קשה מאוד, תלוי בצורה של פונקציית האנרגיה הפוטנציאלית. כפי שמתברר, משוואת שרדינגר מצליחה ביותר בהסבר התנהגות של מערכות אטומיות וגרעיניות, ואילו הפיזיקה הקלאסית נכשלת בהסבר התנהגות זו. יתר על כן, כאשר המכניקה הקוונטית מיושמת על עצמים מקרוסקופיים, התוצאות תואמות את הפיזיקה הקלאסית.

החלקיק בקופסה - חזרה

כדי לראות כיצד מיושם מודל החלקיק הקוונטי תחת תנאי שפה על בעיה, בואו נחזור לחלקיק שלנו בקופסה חד-מימדית באורך (ראו איור 3.2) וננתח אותו עם משוואת שרדינגר. איור 3.3 הוא תרשים האנרגיה הפוטנציאלית המתאר בעיה זו. תרשימי אנרגיה פוטנציאלית הם ייצוג שימושי להבנה ופתרון בעיות עם משוואת שרדינגר.

הערה: בארות פוטנציאל

באר פוטנציאל כמו זו באיור 3.3 היא ייצוג גרפי של אנרגיה, לא ייצוג ציורי, כך שלא הייתם רואים צורה זו אם הייתם יכולים לצפות במצב. חלקיק נע רק אופקית במיקום אנכי קבוע בתרשים אנרגיה פוטנציאלית, המייצג את האנרגיה השמורה של מערכת החלקיק וסביבתו.

בגלל צורת העקומה באיור 3.3, החלקיק בקופסה נאמר לעתים כנמצא בבאר ריבועית, כאשר באר היא אזור הפונה כלפי מעלה של העקומה בתרשים אנרגיה פוטנציאלית. (אזור הפונה כלפי מטה נקרא מחסום, שאותו נחקור בהמשך.) איור 3.3 מראה באר ריבועית אינסופית.

באזור , כאשר , אנו יכולים לבטא את משוואת שרדינגר בצורה:

כאשר:

הפתרון למשוואה (SJ40.16) הוא פונקציה שהנגזרת השנייה שלה היא השלילי של אותה פונקציה כפול קבוע . גם פונקציות הסינוס וגם הקוסינוס מקיימות דרישה זו. לכן, הפתרון הכללי ביותר למשוואה הוא צירוף ליניארי של שני הפתרונות:

כאשר ו- הם קבועים הנקבעים על ידי תנאי השפה והנורמליזציה.

תנאי השפה הראשון על פונקציית הגל הוא ש-:

מה שאומר ש-. לכן, הפתרון שלנו:

תנאי השפה השני, , כאשר מוחל על הפתרון לעיל נותן:

משוואה זו יכולה להיות מקוימת על ידי קביעת , אבל זה יאמר ש- בכל מקום, מה שאינו פונקציית גל תקפה. תנאי השפה מקוים גם אם הוא כפולה שלמה של , כלומר, אם , כאשר הוא מספר שלם.

הצבת בביטוי זה נותנת:

כל ערך של המספר השלם מתאים לאנרגיה מקוונטת שאנו קוראים לה . פתרון עבור האנרגיות המותרות נותן:

שהן זהות לאנרגיות המותרות במשוואה (SJ40.14). הצבת ערכי בפונקציית הגל, פונקציות הגל המותרות נתונות על ידי:

שהיא פונקציית הגל (משוואה (SJ40.12)) ששימשה בדיון הראשוני שלנו על החלקיק בקופסה.

→ קודם: PHY3_002הבא: PHY3_004 ←