PHY3_004 מכניקה קוונטית ב

→ קודם: PHY3_003הבא: PHY3_005 ←

חלקיק בבאר בעלת גובה סופי

כעת נבחן חלקיק בבאר פוטנציאל סופית, כלומר מערכת בעלת אנרגיה פוטנציאלית השווה לאפס כאשר החלקיק נמצא באזור וערך סופי כאשר החלקיק נמצא מחוץ לאזור זה כמו באיור 4.1. קלאסית, אם האנרגיה הכוללת של המערכת קטנה מ-, החלקיק קשור לצמיתות בבאר הפוטנציאל. אם החלקיק היה מחוץ לבאר, האנרגיה הקינטית שלו הייתה צריכה להיות שלילית, מה שבלתי אפשרי.

איור 4.1: תרשים אנרגיה-פוטנציאל של באר בגובה סופי ואורך . אם האנרגיה הכוללת של מערכת החלקיק-באר קטנה מ-, החלקיק לכוד בבאר. (Serway et al., 2019).

על פי המכניקה הקוונטית, עם זאת, קיימת הסתברות סופית שהחלקיק יכול להימצא מחוץ לבאר אפילו אם . כלומר, פונקציית הגל היא בדרך כלל שונה מאפס מחוץ לבאר - אזורים I ו-III באיור 4.1 - כך שצפיפות ההסתברות היא גם שונה מאפס באזורים אלה. למרות שרעיון זה עלול להיות לא נוח לקבלה, עקרון האי-ודאות, משוואה (SJ39.23) מציין שהאנרגיה של המערכת אינה ודאית. אי-ודאות זו מאפשרת לחלקיק להיות מחוץ לבאר כל עוד ההפרה הנראית של שימור האנרגיה אינה קיימת בדרך הניתנת למדידה.

באזור II, כאשר , פונקציות הגל המותרות הן שוב סינוסואידיות מכיוון שהן מייצגות פתרונות של משוואה (SJ40.16). תנאי השפה, עם זאת, אינם דורשים יותר ש- תהיה אפס בקצות הבאר, כפי שהיה המקרה עם הבאר הריבועית האינסופית.

משוואת שרדינגר עבור אזורים I ו-III יכולה להיכתב:

מכיוון ש-, המקדם של בצד ימין הוא בהכרח חיובי. לכן, נוכל לבטא את משוואה (SJ40.20) כ:

כאשר הוא קבוע חיובי באזורים I ו-III. כפי שניתן לוודא על ידי הצבה, הפתרון הכללי של משוואה (SJ40.21) הוא:

כאשר ו- הם קבועים. נוכל להשתמש בפתרון כללי זה כנקודת התחלה לקביעת הפתרון המתאים עבור אזורים I ו-III.

הפתרון חייב להישאר סופי כאשר . לכן, באזור I, כאשר , הפונקציה אינה יכולה להכיל את האיבר . דרישה זו מטופלת על ידי לקיחת באזור זה כדי להימנע מערך אינסופי עבור עבור ערכים שליליים גדולים של . באופן דומה, באזור III, כאשר , הפונקציה אינה יכולה להכיל את האיבר . דרישה זו מטופלת על ידי לקיחת באזור זה כדי להימנע מערך אינסופי עבור עבור ערכי חיוביים גדולים.

לכן, הפתרונות באזורים I ו-III הם:

באזור II, פונקציית הגל היא סינוסואידית ובעלת הצורה הכללית:

כאשר ו- הם קבועים.

תוצאות אלה מראות שפונקציות הגל מחוץ לבאר הפוטנציאל (כאשר הפיזיקה הקלאסית אוסרת על נוכחות החלקיק) דועכות אקספוננציאלית עם המרחק. בערכי שליליים גדולים, מתקרבת לאפס; בערכי חיוביים גדולים, מתקרבת לאפס. פונקציות אלה, יחד עם הפתרון הסינוסואידי באזור II, מוצגות באיור 4.2 עבור שלושת מצבי האנרגיה הראשונים.

איור 4.2: שלושת המצבים המותרים הראשונים עבור חלקיק בבאר פוטנציאל בגובה סופי. המצבים מוצגים מונחים על פונקציית האנרגיה הפוטנציאלית של איור 4.1. פונקציות הגל וצפיפויות ההסתברות מוצגות אנכית מצירים נפרדים המוזחים אנכית לבהירות. המיקומים של הצירים הללו על פונקציית האנרגיה הפוטנציאלית מציעים את האנרגיות היחסיות של המצבים. (Serway et al., 2019).

בהערכת פונקציית הגל השלמה, אנו מטילים את תנאי השפה הבאים:

ארבעת תנאי השפה הללו ותנאי הנורמליזציה (משוואה (SJ40.7)) מספיקים לקביעת ארבעת הקבועים , , , ו- והערכים המותרים של האנרגיה . בכל מקרה, פונקציות הגל בתוך ומחוץ לבאר הפוטנציאל מתחברות בצורה חלקה בגבולות.

מנהור דרך מחסום אנרגיה פוטנציאלית

נבחן את פונקציית האנרגיה הפוטנציאלית המוצגת באיור 4.3. במצב זה, האנרגיה הפוטנציאלית בעלת ערך קבוע באזור ברוחב והיא אפס בכל האזורים האחרים. פונקציית אנרגיה פוטנציאלית בצורה זו נקראת מחסום ריבועי, ו- נקרא גובה המחסום.

איור 4.3: פונקציית הגל עבור חלקיק הפוגע משמאל במחסום בגובה ורוחב . פונקציית הגל מוצגת אנכית מציר הממוקם באנרגיה של החלקיק. פונקציית הגל סינוסואידית באזורים I ו-III, אבל דועכת אקספוננציאלית באזור II. (Serway et al., 2019).

תופעה מעניינת ומוזרה מאוד מתרחשת כאשר חלקיק נע פוגש במחסום כזה בעל גובה ורוחב סופיים. נניח שחלקיק בעל אנרגיה פוגע במחסום משמאל (איור 4.3). קלאסית, החלקיק מוחזר על ידי המחסום. אם החלקיק היה ממוקם באזור II, האנרגיה הקינטית שלו הייתה שלילית, מה שאינו מותר קלאסית. כתוצאה מכך, אזור II ולכן גם אזור III אסורים קלאסית לחלקיק הפוגע משמאל.

על פי המכניקה הקוונטית, עם זאת, כל האזורים נגישים לחלקיק, ללא קשר לאנרגיה שלו. (למרות שכל האזורים נגישים, ההסתברות שהחלקיק יהיה באזור האסור קלאסית נמוכה מאוד.) על פי עקרון האי-ודאות, החלקיק יכול להיות בתוך המחסום כל עוד מרווח הזמן שבו הוא במחסום קצר ועקבי עם משוואה (SJ39.24). אם המחסום צר יחסית, מרווח זמן קצר זה יכול לאפשר לחלקיק הפוגע משמאל להופיע בצד ימין של המחסום.

בואו ניגש למצב זה באמצעות ייצוג מתמטי. למשוואת שרדינגר יש פתרונות תקפים בכל שלושת האזורים. הפתרונות באזורים I ו-III הם סינוסואידיים כמו משוואה (SJ40.19). באזור II, הפתרון הוא אקספוננציאלי כמו משוואה (SJ40.22) לעיל. החלת תנאי השפה שפונקציות הגל בשלושת האזורים והנגזרות שלהן חייבות להתחבר בצורה חלקה בגבולות, פתרון מלא, כמו זה המיוצג על ידי העקומה באיור 4.3, יכול להימצא.

מכיוון שההסתברות לאיתור החלקיק פרופורציונלית ל-, ההסתברות למציאת החלקיק מעבר למחסום באזור III אינה אפס. תוצאה זו נמצאת בחוסר הסכמה מוחלט עם הפיזיקה הקלאסית. הופעת החלקיק בצד הרחוק של המחסום מתוארת כחלקיק הנע דרך המחסום משמאל לימין, ולכן היא נקראת מנהור או חדירת מחסום.

הערה: "גובה" בתרשים אנרגיה

איור 4.4: המילה גובה (כמו בגובה מחסום) מתייחסת לאנרגיה בדיונים על מחסומים בתרשימי אנרגיה פוטנציאלית. לדוגמה, נוכל לומר שגובה המחסום הוא . מצד שני, רוחב המחסום מתייחס לשימוש המסורתי של מילה כזו והוא מדידת אורך פיזית ממשית בין המיקומים של שני הצדדים האנכיים של המחסום.

ההסתברות למנהור יכולה להיות מתוארת עם מקדם העברה ומקדם החזרה . מקדם ההעברה מייצג את ההסתברות שהחלקיק חודר לצד השני של המחסום, ומקדם ההחזרה הוא ההסתברות שהחלקיק מוחזר על ידי המחסום. מכיוון שהחלקיק הפוגע או מוחזר או מועבר, אנו דורשים ש-.

ביטוי משוער למקדם ההעברה המתקבל במקרה של (מחסום רחב מאוד או מחסום גבוה מאוד, כלומר ) הוא:

כאשר:

המודל הקוונטי הזה של חדירת מחסום ובמיוחד משוואה (SJ40.28) מראים ש- יכול להיות שונה מאפס. העובדה שהתופעה של מנהור נצפית בניסויים מחזקת עוד יותר את הביטחון בעקרונות הפיזיקה הקוונטית.

דוגמה: מקדם העברה עבור אלקטרון

אלקטרון בעל אנרגיה פוגע במחסום ריבועי בגובה .

מה ההסתברות שהאלקטרון ינהר דרך המחסום אם רוחבו הוא ננומטר?

פתרון:

מכיוון שאנרגיית החלקיק קטנה מגובה מחסום הפוטנציאל, אנו מצפים שהאלקטרון יוחזר מהמחסום עם הסתברות של על פי הפיזיקה הקלאסית. בגלל תופעת המנהור, עם זאת, יש הסתברות סופית שהחלקיק יכול להופיע בצד השני של המחסום.

נחשב את הכמות המופיעה במשוואה (SJ40.29):

נחשב את הכמות באמצעות משוואה (SJ40.29):

ממשוואה (SJ40.28), נמצא את ההסתברות למנהור דרך המחסום:

מה ההסתברות שהאלקטרון ינהר דרך המחסום אם רוחבו הוא ננומטר?

במקרה זה, הרוחב קטן פי עשרה, כך ש:

ההסתברות החדשה למנהור דרך המחסום:

בחלק הראשון, לאלקטרון יש בקירוב סיכוי אחד ב- לנהור דרך המחסום. בחלק השני, עם זאת, לאלקטרון יש הסתברות גבוהה בהרבה () לחדור את המחסום. לכן, הפחתת רוחב המחסום בסדר גודל אחד בלבד מגדילה את ההסתברות למנהור בכ- סדרי גודל!

מתנד הרמוני פשוט

נחקור חלקיק הכפוף לכוח אלסטי ליניארי , כאשר הוא קבוע ו- הוא מיקום החלקיק יחסית לשיווי משקל (). התיאור הקלאסי של מצב כזה מסופק על ידי מודל האנליטי של החלקיק בתנועה הרמונית פשוטה.

האנרגיה הפוטנציאלית של המערכת היא:

כאשר התדירות הזוויתית של הרטט היא .

קלאסית, אם החלקיק מוזז ממיקום שיווי המשקל ומשוחרר, הוא מתנדנד בין הנקודות ו-, כאשר הוא משרעת התנועה. יתר על כן, האנרגיה הכוללת שלו היא:

במודל הקלאסי, כל ערך של מותר, כולל , שהיא האנרגיה הכוללת כאשר החלקיק במנוחה ב-.

בואו נחקור כיצד המתנד הרמוני פשוט מטופל מנקודת מבט קוונטית. משוואת שרדינגר עבור בעיה זו מתקבלת על ידי הצבת במשוואה (SJ40.15):

הטכניקה המתמטית לפתרון משוואה זו מעבר לרמת הקורס הזה; עם זאת, נוכל לנחש פתרון. אנו לוקחים כניחוש שלנו את פונקציית הגל הבאה:

הצבת פונקציה זו במשוואה (SJ40.31) מראה שהיא פתרון מספק למשוואת שרדינגר, בתנאי ש:

מתברר שהפתרון שניחשנו מתאים למצב היסוד של המערכת, שיש לו אנרגיה . מכיוון ש-, נובע ממשוואה (SJ40.32) שפונקציית הגל עבור מצב זה היא:

כאשר הוא קבוע שיקבע מתנאי הנורמליזציה.

תוצאה זו היא רק פתרון אחד למשוואה (SJ40.31). הפתרונות הנותרים המתארים את המצבים המעוררים מורכבים יותר, אבל כל הפתרונות כוללים את הגורם האקספוננציאלי .

רמות האנרגיה של מתנד הרמוני מקוונטות כפי שהיינו מצפים מכיוון שהחלקיק המתנדנד קשור להישאר ליד . האנרגיה של מצב בעל מספר קוונטי שרירותי היא:

המצב מתאים למצב היסוד, שהאנרגיה שלו היא ; המצב מתאים למצב המעורר הראשון, שהאנרגיה שלו היא ; וכן הלאה.

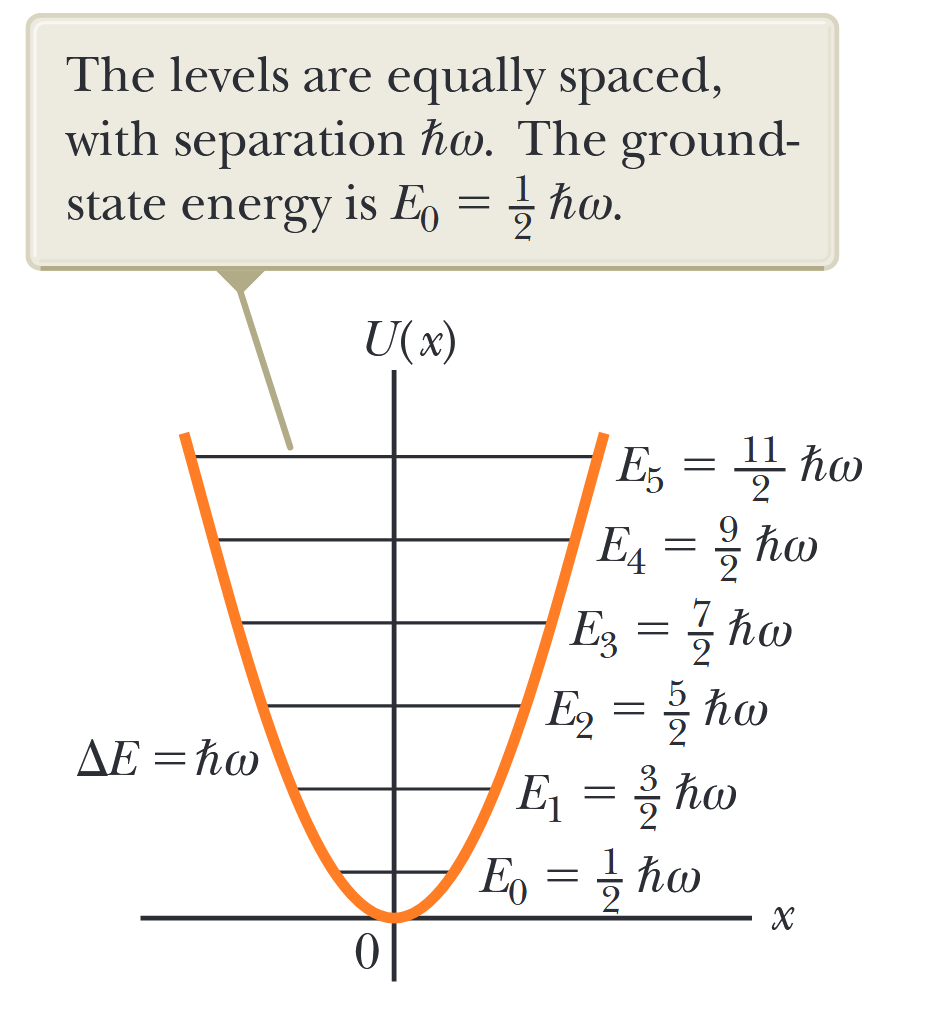
תרשים רמות אנרגיה עבור מתנד הרמוני פשוט, מונח על פונקציית האנרגיה הפוטנציאלית. הרמות מרווחות באופן שווה, עם הפרדה . אנרגיית מצב היסוד היא . (Serway et al., 2019).

ההפרשים בין רמות סמוכות שוות ונתונות על ידי:

שימו לב שרמות האנרגיה עבור המתנד הרמוני באיור 4.4 מרווחות באופן שווה, בדיוק כפי שהציע פלאנק עבור המתנדים בקירות החלל ששימש במודל לקרינת גוף שחור. למעשה, המרווח בין הרמות זהה בדיוק למרווח של פלאנק, כפי שניתן לראות על ידי השוואת משוואות (SJ39.5) ו-(SJ40.35)! זה מייצג קשר מדהים נוסף בין גישה חצי-קלאסית, כמו זו של פלאנק, לגישה הקוונטית המלאה הנדונה כאן.

משוואת פלאנק עבור רמות האנרגיה של המתנדים שונה ממשוואה (SJ40.34) רק באיבר המתווסף ל-. איבר נוסף זה אינו משפיע על האנרגיה הנפלטת במעבר.

דוגמה: חום סגולי מולרי של גז מימן

בגרף החום הסגולי המולרי של מימן כפונקציה של הטמפרטורה, רטט אינו תורם לחום הסגולי המולרי בטמפרטורת החדר. הסבירו מדוע, תוך מדול מולקולת המימן כמתנד הרמוני פשוט. קבוע הקפיץ האפקטיבי עבור הקשר במולקולת המימן הוא .

פתרון:

דמיינו את אופן הרטט היחיד הזמין למולקולה דו-אטומית. אופן זה מורכב משני האטומים הנעים תמיד בכיוונים מנוגדים במהירויות שוות.

נקטלג דוגמה זו כבעיית מתנד הרמוני קוונטי, עם המולקולה ממודלת כמערכת של שני חלקיקים.

התנועה של החלקיקים יחסית למרכז המסה יכולה להיות מנותחת על ידי בחינת התנדנדות של חלקיק יחיד עם מסה מופחתת .

נשתמש בתוצאה לחישוב המסה המופחתת של מולקולת המימן, בה מסות שני החלקיקים זהות:

באמצעות משוואה (SJ40.35) ו-, נחשב את האנרגיה הדרושה לעורר את המולקולה ממצב הרטט הבסיסי שלה למצב הרטט המעורר הראשון:

נציב ערכים מספריים, כאשר אנו שמים לב ש- היא מסת אטום מימן:

נקבע את האנרגיה הזו כשווה ל- ונמצא את הטמפרטורה שבה האנרגיה הקינטית הממוצעת של המולקולה שווה לזו הנדרשת לעורר את מצב הרטט הראשון של המולקולה:

הטמפרטורה של הגז חייבת להיות יותר מ- כדי שהאנרגיה הקינטית של המולקולה תהיה דומה לאנרגיה הנדרשת לעורר את מצב הרטט הראשון. אנרגיית הגירוי הזו חייבת להגיע מהתנגשויות בין מולקולות, אז אם למולקולות אין אנרגיה קינטית מספקת, הן אינן יכולות להיות מעוררות למצב הרטט הראשון והרטט אינו תורם לחום הסגולי המולרי.

→ קודם: PHY3_003הבא: PHY3_005 ←