SLD1_001 הקדמה ומושגי יסוד

→ קודם: SLD1_000הבא: SLD1_002 ←

הקדמה - הגדרות ופעולות

מוסכמות

מכניקה - ענף של פיזיקה העוסק בתגובה של חומרים ומבנים לעומסים שפועלים עליהם.
נהוג לחלק את המכינקה לסטטיקה ודינמיקה.
סטטיקה - גוף בשיווי במשקל (ש”מ).
דינמיקה - גוף שאינו בשיווי משקל.

סימונים:
בהינתן שני גופים , נסמן את הכוח ש- מפעיל על ב- או (מודגש). נשים לב כי זהו שונה מהסימון הידוע . באותו אופן, נסמן את הכוח ש- מפעיל על ב-.

את וקטורי היחידה נסמן במקום בסימונים . בנוסף, את נרמול הוקטור , נסמן ב- במקום .

וקטורים

פעולות וקטוריות

• מכפלה סקלרית - למדו בחדו”א 2:
• נרמול - למדנו בחדו”א 2:
• מכפלה וקטורית - למדנו בחדו”א 2: כאשר: וגודל זה הוא שטח המקבילית הנוצרת בין ו-.
  הכיוון של הוא ניצב למישור שמוגדר ע”י ו-.
  בהינתן ו-, נוכל לחשב את בעזרת דטרמיננטה:

כוחות

כוח

ניזכר בכוח מפיזיקה.
כוח הוא אמצעי שבעזרתו מרגיש גוף אחד בנוכחות השני.

וואלה מגניב. הגדרה מאוד כללית ומופשטת. אבל כוח הוא באמת כך - מופשט, ואף מושג פילוסופי. את הכוחות בקורס זה לרוב נסמן באות , והוא יהיה בין שניים או יותר גופים.

כוחות מרכזיים

בהינתן שני חלקיקים , הכוח ש- מפעיל על , ו- מפעיל על - נקראים כוחות מרכזיים. הם נקראים כך כיוון שכוחות אלו פועלים לכיוון “המרכז” של ו-.

מומנט

• מומנט בפיזיקה.

מעבר מהנטייה להזיז גוף בכיוון מסוים, כוח יכול גם לגרום לגוף להסתובב סביב ציר מסוים. ציר זה יכול להיות כל קו שלא חותך או מקביל לכיוון הכוח. הנטייה הסיבובית הזאת נקראת מומנט של הכוח. מומנט נקרא גם טורק ().

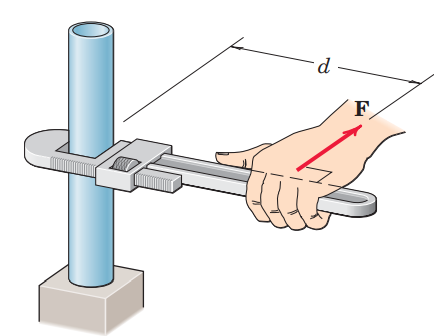
הכוח שמפעילה היד על המפתח יוצר מומנט סביב העמוד.

הגדרה:

בהינתן כוח ונקודה במרחב , המומנט סביב הנקודה , המסומן מוגדר כך:

כאשר הוקטור הוא וקטור המרחק מ- ל-.

הערות:

1. נשים לב כי מההגדרה נובע כי גודל המומנט תלוי במרחק של מנקודת הפעלת הכוח, וגם בגודל הכוח:

2. ממד הגודל הזה הוא כוח כפול מרחק:

3. זוהי מכפלה וקטורית, ולכן כיוון המומנט הוא בכיוון המאונך ל- ו-. באיור של המפתח, המומנט הוא בכיוון כלפי מעלה (לפי כלל יד ימין). למעשה, לפי כלל יד ימין, נוכל להסיק את הכיוון בו הצינור יסתובב (נגד כיוון השעון):
   
4. גודל המומנט תלוי בגודל הכוח ובמרחק של נקודת הייחוס מקו הפעולה של . לכן, הזזה של הכוח לאורך קו הפעולה לא משנה את המומנט שהוא יוצר.

משפט ואריגנון

משפט:

המומנט השקול הנוצר ממספר כוחות שווה לסכום המומנטים של כלל הכוחות:

עבור גוף בשיווי משקל המומנט מתאפס לכל נקודה

משפט:

אם וגם עבור נקודה כלשהי, אז ביחס לכל נקודה במרחב.

הוכחה:
נתון כי:

וגם:

---

תרגיל:
נתון התרשים הבא:

מהו המומנט שמפעיל הכוח ביחס לנקודה בה נמצא הבורג?
פתרון:
לפי הגדרת המומנט:

נחשב את שני הוקטור ואת הכוח:

נציב ונקבל:

---

תרגיל:

פלטה מרובעת נתמכת ע”י צירים לאורך הקו ובאמצעות כפל כאשר הנקודה נמצאת במרכז הקטע . נסמן את וקטור המתיחות של הכפל באמצעות . בנוסף, גודל המתיחות בכבל . את הזווית באיור שמוגדרת כ- נסמן ב-.
בנוסף, נתון כי ו- .

1. מהו כיוון המישור של המישור העליון של הפלטה ?
   פתרון:
   נתון כי במרכז . כיוון מישור :
   ניתן להגדיר מישור ע”י הנורמל למישור. כדי למצוא את הנורמל, נבצע מכפלה וקטורית: נחזור לשאלה. נרצה לחשב: אז נשים לב כי: וכעת נוכל לחשב:
2. מהו היטל על ?
   פתרון:
   נסמן ב- את ההיטל: נבצע מכפלה סקלרית (פנימית): וכעת:
3. מהו רכיב הכוח שניצב ל-?
   פתרון:
   נסמן את הניצב ב-.
4. מהו מומנט ביחס ל-?
   פתרון:

---

תרגיל:

נתונה המערכת המתוארת בציור שעלה פועל הכוח. דרוש לחשב את המומנט שיוצר הכוח על הנקודה .

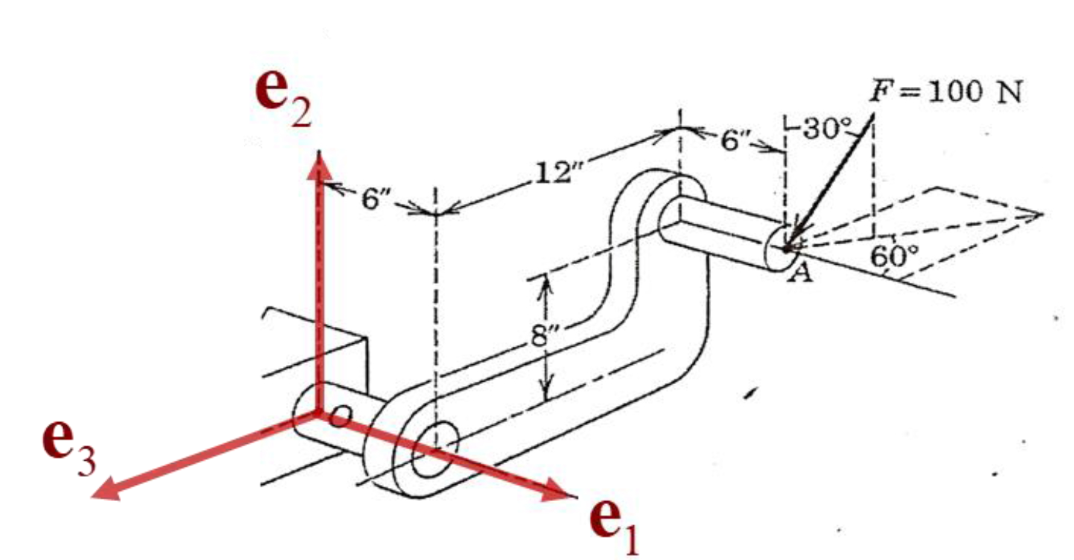
פתרון:

---

תרגיל:

נתון המבנה של מנורת רחוב כמתואר בציור. המנורה מקובעת לבסיס שמפעיל עליה בנק’ כוח שקול ומומנט טהור שקול.
מסת המבנה זניחה ביחס לכוחות הפועלים על המבנה.
מהו המומנט השקול שיוצרים הכוחות על המבנה ביחס לנקודה ?

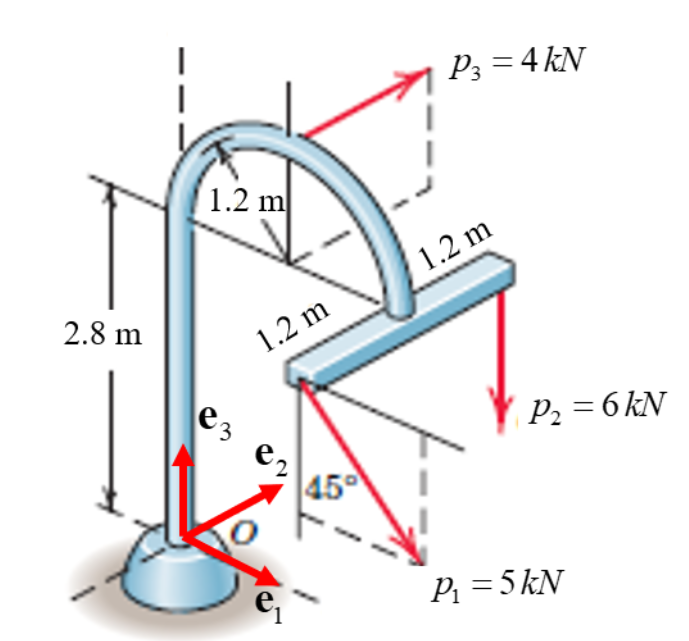
פתרון:

וכעת נוכל לחשב:

ומפה אין לנו כוח לחשב יותר.

מומנט טהור

המומנט שנוצר ע”י שתי כוחות שווים ומנוגדים בכיוונם שאינם קווים (לא מתלכדים), נקרא מומנט טהור.

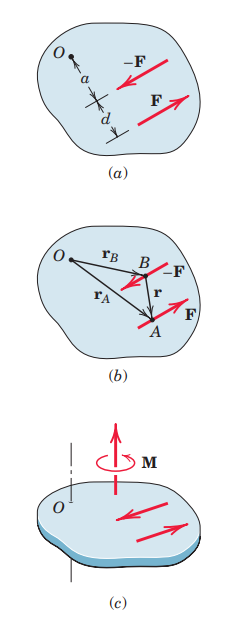
נביט באיור ונתייחס לשתי הכוחות המנוגדים ו-, במרחק אחד מן השני. התוצאה של שני כוחות אלו היא ליצור נטייה לסיבוב - מומנט. המומנט ששני הכוחות מייצרים סביב ציר המאונך למישור ושחותך את המישור דרך כל נקודה כמו במישור הוא המומנט הטהור .

גודל המומנט נתון ע”י:

כלומר:

הערות:

1. הכוח השקול של מומנט טהור הוא אפס.
2. נשים לב כי התוצאה לא תלויה בבחירה של , אלא רק במרחק בין הכוחות, .
3. גודל המומנט הטהור תלוי בגודל הכוחות ובמרחק בין קווי הפעולה שלהם.

מומנט סביב ציר

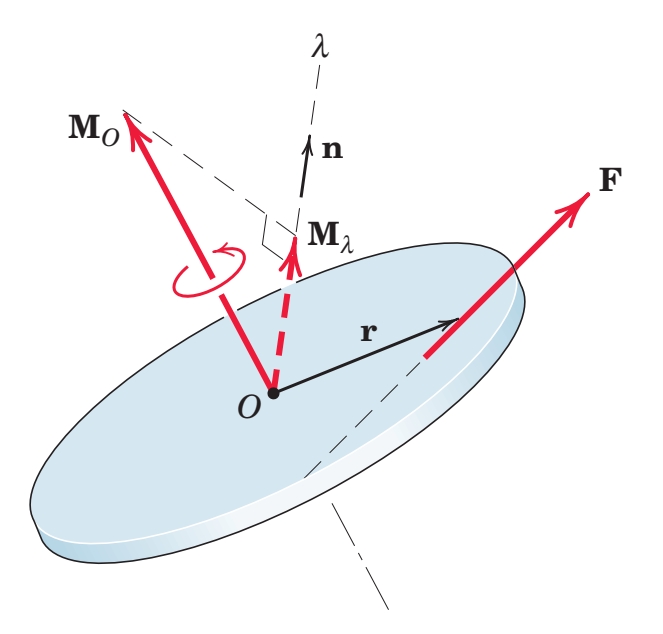
על מנת למצוא את הביטוי עבור מומנט של כוח של כל ציר העובר דרך , נוכל לבצע את החישוב הבא כדי למצוא את גודלו:

כאשר הוא כיוון הציר .
אנו מבצעים את המכפלה הסקלרית () על מנת למצוא את ההיטל של על הציר .
כמובן, כיוונו יהיה כיוון הציר, , ולכן נוכל לסכם:

נוסחה:

הערות:

1. כאשר אנו מחשבים מומנט סביב ציר, יש לחשב את המומנט ביחס לנקודה כלשהי על הציר ולהטיל את המומנט בכיוון הציר.
2. בשיווי משקל, סכום המומנטים סביב ציר חייב להתאפס:

3. המומנט של כוח מסוים סביב ציר מתאפס אם:

• קו הפעולה של הכוח חותך את הציר (לא משנה באיזה זווית).
• קו הפעולה של הכוח מקביל לציר.

מערכת כוח-מומנט (טהור)

התוצאה של כוח המופעל על גוך היא הנטייה של הגוף להימשך או להידחף בכיוון הכוח, והנטייה לסובב את הגוף סביב ציר קבוע שלא נחתך עם קו הכוח.
ניתן לתאר את האפקט הכפול הזה יותר בקלות ע”י החלפת הכוח הנתון ע”י כוח שווה ומקביל, בנוסף למומנט טהור שמקזז את השינוי במומנט של הכוח.

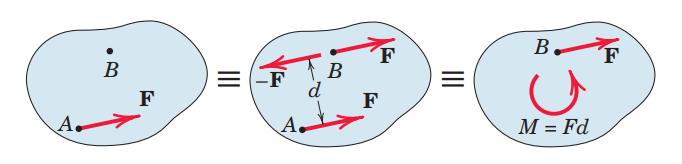
באיור זה ניתן לראות את ההחלפה של כוח הפועל בנקודה - לכוח שווה היוצא מנקודה והמומנט הטהור נגד כיוון השעון.
בשלב האמצעי מוסיפים שני כוחות ו- הפועלים על נקודה . שני כוחות אלו מבטלים אחד את השני ולכן מותר לנו להוסיף אותם מבלי לשנות את המערכת. כעת, ניתן לראות שיש לנו מומנט טהור שנוצר ע”י כוח שפועל על , וכוח שפועל על נקודה .
בנוסף, המומנט הטהור נתון באופן הבא:

נאמר שהמערכת שהייתה לנו בהתחלה והמערכת שקיבלנו בסוף הן מערכות שקולות. למערכת החדשה שקיבלנו נקרא מערכת כוח-מומנט.

שקול

השקול של מערכת כוחות היא הקומבינציית כוחות הפשוטה ביותר שיכולה להחליף את הכוחות המקוריים, בלי לשנות אפקטים חיצוניים על הגוף הקשיח שמופעלים עליו הכוחות. כיצד ניתן לחשב שקול זו? ניקח דוגמה בדו-ממד:

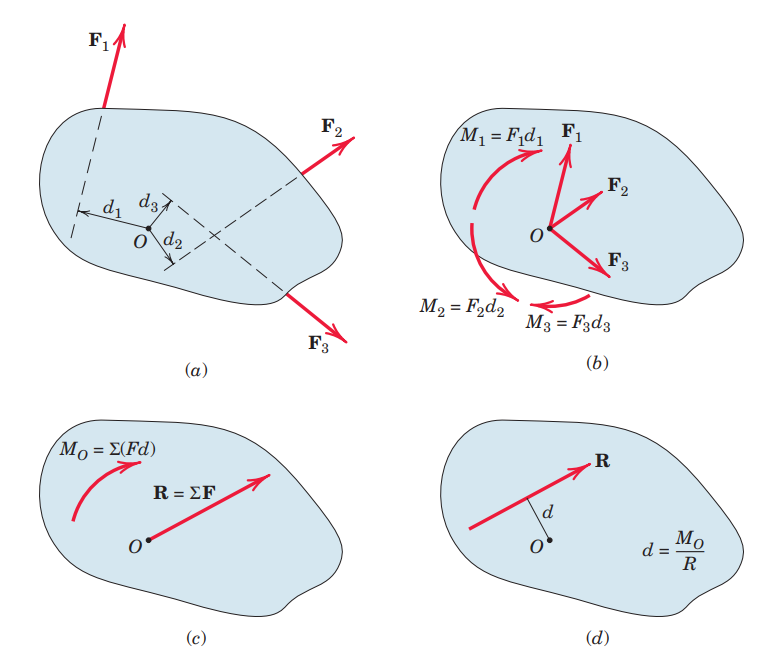
1. נבחר נקודה נוחה לראשית הצירים, ונזיז את כל הכוחות לנקודה זו. בחלק ניתן לראות את פעולה זו, ובנוסף נשים לב לכל המומנטים הטהורים שהתווספו לפי מערכת כוח-מומנט (טהור).
2. נסכום את כל הכוחות ב- כדי לקבל את השקול , ונסכום את כל המומנטים הטהורים כדי ליצור את התגובת מומנטים . כעת יש לנו מערכת כוח-מומנט.
3. בחלק של האיור נמצא את קו הפעולה של בכך שנדרוש שיהיה לו מומנט סביב נקודה . נשים לב כי שתי המערכות ב- וב- הן מערכות שקולות.

ניתן לסכם את הפעולות האלו בביטוי הבא, שהוא למעשה הרחבה של משפט ואריגנון שנקרא עיקרון המומנטים או עיקרון הסופרפוזיציה למומנטים:

עיקרון המומנטים

משפט:

בשתי המשוואות הראשונות אנו מתארים את המערכת כמערכת כוח-מומנט.
המשוואה השלישית מתארת את המרחק מהנקודה לקו הפעולה של ואומרת כי המומנט של כוח השקול סביב כל נקודה שווה לסכום המומנטים של הכוחות המקוריים סביב אותה נקודה.

---

הערה:

עבור תרגילים אלו מניחים כי אנו כבר יודעים על שיווי משקל.

תרגיל:
נתונה מערכת צירים . שלושה חוטים יוצאים מהנקודה לנקודות ו-. לצורך נוחות, נבחר את ראשית הצירים בנקודה , כמו בציור.

ידוע כי הכוח הפנימי בחוטים הוא כוח מתיחה הפועל בכיוון החוטים למרכזם.
מפעילים בנקודה כוח: .
מגבלת הכוח המקסימלי בכל אחד מהחוטים זהה והיא: . כלומר כדי שהחוטים לא יקרעו, חייב לקיים: .
למה שווה ?
פתרון:
משוואת כוחות על נקודה :

נבטא את :

נבטא את המתיחות:

נפתור את המשוואה:

קיבלנו כי:

מאחר ו- נושאים בחלק גדול מהעומס של , הדרישה ל- תגיע מהם.

ולכן:

---

תרגיל:

נתונים שלושה חלקיקים חסרי משקל המחוברים באמצעות חוטים.
יש למצוא את המתיחות בכל אחד מהחוטים.

פתרון:
נשים לב כי מתיחות הוא כוח פנימי הפועל בכיוון החוט למרכז.

עבור החלקיק השלישי:

עבור החלקיק השני:

עבור החלקיק הראשון:

עבור כלל הגוף:

---

→ קודם: SLD1_000הבא: SLD1_002 ←