SLD1_005 מהלכי כוחות ומומנטים בקורות

→ קודם: SLD1_004הבא: SLD1_006 ←

קורות - עומסים פנימיים

מעבר לכוחות מתיחה ולחיצה, קורה יכולה להפעיל עומסים פנימיים - כוחות גזירה (shear), מומנטי כפיפה (bending), ומומנט פיתול (torsion).

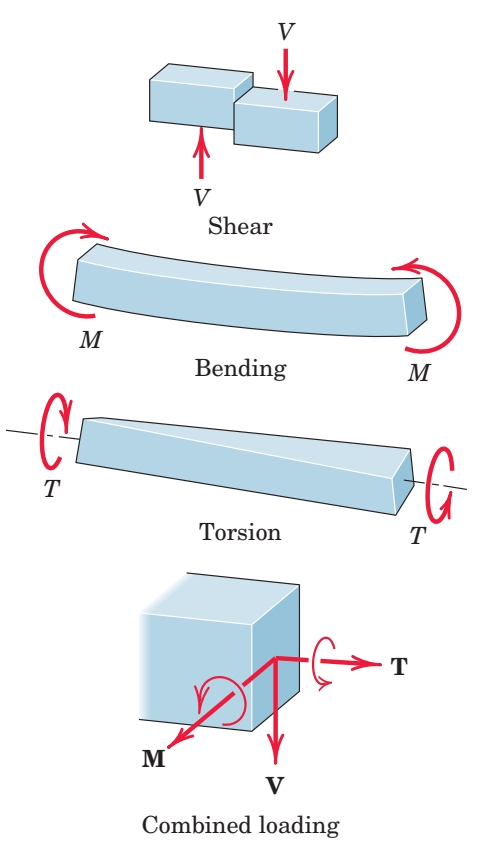
כאינטואיציה למומנט כיפוף, נביט בקורה הבאה:

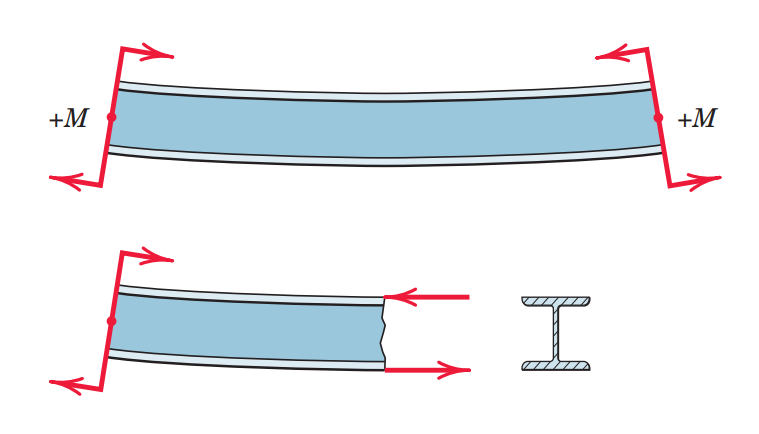
קורה זה מכופפת ע”י שני מומנטים שווים ומנוגדים בקצוות. הקטע העליון של הקורה מתקצר ונמצא תחת לחיצה, לעומת הקטע התחתון שמתארך ונמצא תחת מתיחה. העומס השקול הוא מומנט טהור בעל גודל של מומנט הכיפוף על הקורה.

קורה מישורית

במקרה המישורי, נתעסק רק בכוחות הגזירה והכיפוף.
כוחות אלו פועלים לאורך כל הקורה, כאשר תחת עומסים שונים הפועלים על הקורה, נקבל כוחות גזירה ומומנטי כיפוף שונים עבור חלקים שונים של הקורה.

על מנת לחקור את כוחות פנימיים אילו, נבצע חתכים לאורך הקורה. בהמשך נראה כי הכי נוח לבצע חתכים בנקודות מפנה כדי להסיק מהי התפלגות הכוחות.

נביט בקורה בש”מ הרתומה לקיר באופן הבא:

כפי שרואים בשרטוט, כבר ביצענו חתך על הקורה בנקודה מסוימת. אנו יודעים מבידוד מערכת, שאם גוף נמצא בש”מ, כל חלק שנוציא ממנו (דמיונית), יפעלו עליו כוחות ומומנטים מבחוץ, בנקודות המגע, ככה שגם הוא יהיה בש”מ.

עבור הקורה שלנו באיור, נביט בחתך:

הוצאנו תגובות - (כוח) ו- (מומנט טהור) הפועלים בנקודת המגע של החתך עם חלקה הימני של הקורה. עומסים אלו צוירו בכיוונים סתמיים - הרי אנחנו כעת לא יודעים את גודלם וכיוונם. אז נחשב את ו-:
משיווי משקל כוחות:

מומנטים:

כפי שהצגנו בתחילת הפרק, הוא למעשה כוח הגזירה, ונסמנו - וכפי שראינו כאן, הוא מאונך לנורמל היוצא מהחתך. המומנט הטהור הוא כוח הכפיפה הפועל בכיוון במקרה המישורי.

כיצד נראה פילוג הכוחות לאורך הקורה? נוכל לבנות דיאגרמת פילוג כוחות ומומנטים:

גרף זה מראה לנו בצורה מאוד פשוטה ואינטואיטיבית היכן הנקודה הכי מסוכנת בקורה. כאן ניתן לראות שהנקודה הכי מסוכנת למעשה נמצאת ב-.

על מנת להיות עקביים בבחירת הכיוונים, נשרטט את וקטור הנורמל לחתך - . אם הוא בכיוון החיובי של הצירים, נקרא לחתך חתך חיובי, ונשרטט את עומסי התגובה ו- בכיוונים החיוביים.
אם בכיוון השלילי, נקרא לו חתך שלילי, ונשרטט את ו- בכיוונים השליליים:

בספרות, מקובל תמיד לסמן את הכיוון כלפי מטה כהכיוון החיובי, ואז:

כדי לדעת איפה הכי נוח לבצע את החתכים על מנת להסיק מהי התפלגות הכוחות, נמצא נקודות מפנה. נקודות המפנה הן כאשר יש:

• שינוי גאומטרי בצורת הקורה, או
• שינוי בעומס חיצוני (כוח או מומנט חיצוני).

בנקודות מפנה אילו, ישנו חשד לאי רציפות ושינוי גודל העומסים (כוחות גזירה או כיפוף), ולכן נבצע חתכים בין נקודות מפנה אלו כדי לחשת את התפלגות הכוחות.

קורה תלת ממדית

כפי שנאמר בתחילת הפרק, בקורה תלת ממדים יש לנו מספר עומסים נוספים היכולים לפעול עליה:

כאשר:
הוא כוח הנורמל (מתיחה/לחיצה), הם הכוחות גזירה.
בנוסף, יש לנו את המומנטים הטהורים: המומנט פיתול, מומנטי כיפוף.

קורות - עומסים מפורסים

עומס מפורס

הקורות שעסקנו בהם בפרק הקודם היו תחת עומסים נקודתיים. נעבור כעת למקרים בהם העומסים פרוסים לאורך קטע מן הקורה.

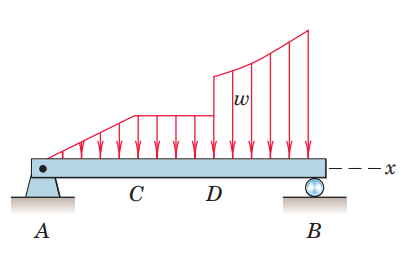
עוצמת העומס המפורס/מחולק/מפוזר ניתנת להצגה ככוח ליחידת אורך. היא יכולה להיות קבועה, או משתנה, כפי שמוצג באיור. כמו כן העומס לא חייב להיות רציף, וגם קצב שינוי העומס לאורך הקורה () לא חייב להיות רציף.

עבור עומסים קבועים או לינאריים קל לנו למצוא את שקול העומס הכולל () הפועל על הקורה:

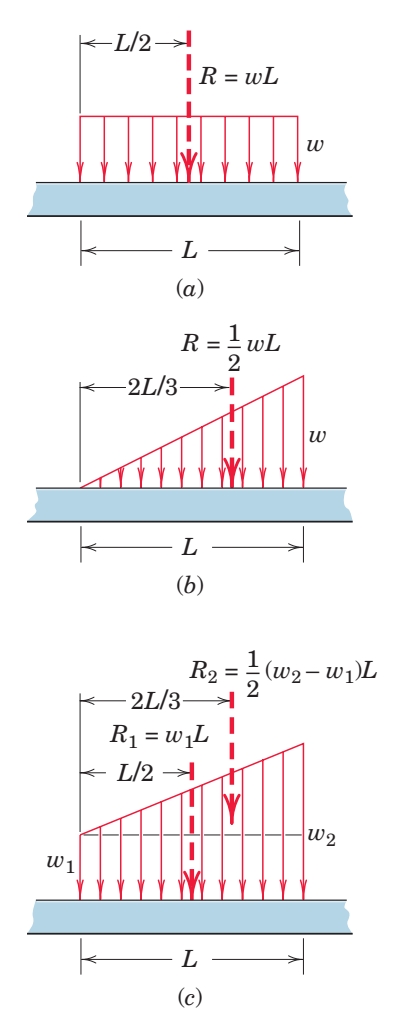
עבור המקרים הפשוטים ב-, עומס התגובה ניתן לחישוב ע”י חישוב פשוט של השטח מתחת ל-. חישוב זה נכון גם עבור מקרה , בו פשוט נפרק את הטרפז לשני חלקים - משולש ומלבן.

איפה פועל הכוח השקול ? הוא פועל במרכז מסה של העומס המפורס - מה שנקרא גם מרכז הלחץ. בכלל האיורים ניתן לראות את נקודה זו. נראה בהמשך כיצד לחשב אותה.

עבור עומסים מפרוסים יותר כלליים, נצטרך לבצע אינטגרל:

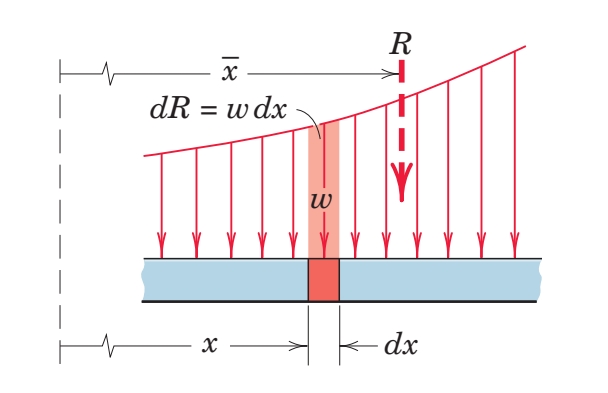
כמו מקודם, ה- (הכוח השקול של העומס המפורס) פועל במרכז המסה של העומס. ה- של מרכז עומס זה ניתן לחישוב ע”י:

קשרים דיפרנציאליים

לכל קורה תחת עומס מפורס ניתן לבנות קשר כללי בין העומסים הפנימיים לאורך הקורה - לעומס המפורס.

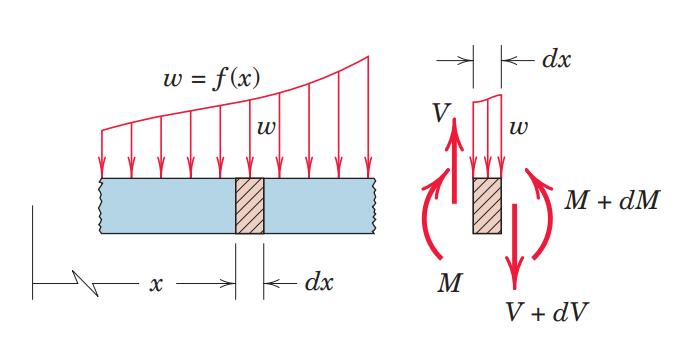
שימו לב! הכיוונים הם:

באיור הנ”ל ניתן לראות קטע מקורה, כאשר התת-קטע שלה מודגש. העומס מציג את העומס ליחידת אורך של קורה. בנקודה כוח הגזירה והמומנט על התת-קטע מוצגים בכיוונם החיובי.

בצד השני של התת-קטע, בנקודה , העומסים הפנימיים גם מוצגים בערכם החיוביים. הפעם הם מסומנים ו-, הרי ו- משתנים כתלות ב-.

ככל ש- שואף לאפס, ניתן לומר כי העומס נהיה קבוע (שימו לב כי הוא פונקציה של , כלומר: ). לכן נוכל לומר כי הכוח השקול הפועל על התת קטע הוא .

משיקולי שיווי משקל, סכום הכוחות האנכיים מתאפסים. לכן:

כלומר:

אנחנו בעצם טוענים פה שהעומס המפורס (שהוא בעצם כוח ליחידת אורך) הוא מינוס הנגזרת של כוח הגזירה לפי .

נוכל לטעון גם שמשיקולי שיווי משקל, סכום המומנטים מתאפס. סכום מומנטים סביב הנקודה השמאלית:

כאשר המכפלה היא המומנט ש- מפעילה, כאשר אנו מניחים כי הכוח פועל במרחק מהנקודה השמאלית של . למה? כי שקול העומס פועל ממרכזו, ועוד דברים שלא למדנו עדיין, ומרכזו כאן הוא ב- כי אנחנו מניחים ש- קבוע.

נוכל לסדר את המשוואה ולקבל:

כלומר, כוח הגזירה הוא נגזרת של המומנט לפי .

נסכם:

קשרים אלו מאוד תלויים בבחירת המערכת צירים שלנו. לכן גם נהיה קצת יותר מדויקים באיזה כיוון כוחות אנו עוסקים:

אם יש לנו מערכת צירים כזאת:

ונבצע את אותם החישובים שעשינו למעלה, מאחר ו-, לעומת , נקבל כי:

במקרה התלת ממדי:

הנוסחאות יישארו אותו הדבר, כי כבר הכללנו אותם לשני הכיוונים:

נוסחה:

תנאי שפה

בהינתן עומס מפורס על קורה כלשהי, ראינו שאנו יכולים למצוא את ו-. אבל, כאשר אנו מבצעים אינטגרל, אנו צריכים תנאי שפה כלשהם כדי לקבל פונקציה אחת בלי קבוע מעצבן. כלומר, אנחנו צריכים ו- כלשהם.

הכי קל לנו למצוא את ו- בקצוות הקורה, ולכן הם יהוו את תנאי השפה שלנו ונסמנם ו-. נתייחס למקרה הפרטי הבא:

משיקולי כוחות על המערכת, נוכל להסיק כי:

משיקולי סימטריה:

אנו יודעים כי:

כעת עלינו למצוא , שהכי קל לנו למצוא אותו בקצה הקטע. כלומר כאשר . אנחנו כאלו עושים חתך על נקודה , אבל לבצע חתך בנקודה זו זה שקול לדג”ח החיצוני שכבר קיים. כוח הגזירה בחתך זה הוא פשוט . כלומר:

לכן נוכל לכתוב:

תרגילים:

1. נתון:
   
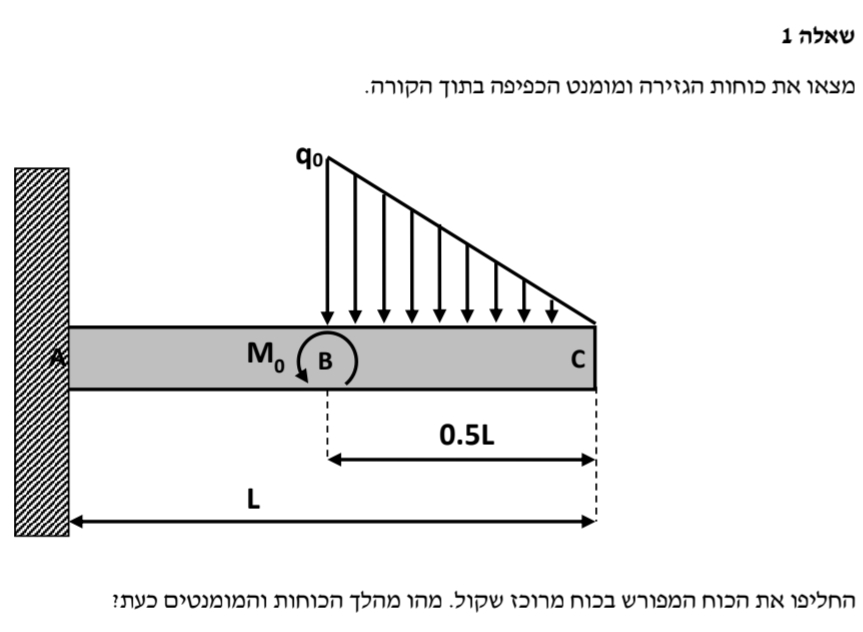
   פתרון:
   נשרטט את המערכת השקולה:
   
   כאשר נשים לב כי הוא הכוח השקול שהעומס המפורס מפעיל על הקורה (כאן סימנו , למעלה סימנו אותו ב-). בנוסף, מתקיים: כי העומס המפורס הוא בצורת משולש (נטו חישוב שטח משולש).
   נבצע חתכים:
   חתך (השלילי):
   החתך (השלילי):
   
   העומס המפורס עד החתך (מדימיון משולשים):
   
   נחשב את הכוח השקול שהעומס המפורס עד החתך מפעיל:
   
   משיווי משקל נובע:
   

→ קודם: SLD1_004הבא: SLD1_006 ←