SLD1_004 עבודה וירטואלית

→ קודם: SLD1_003הבא: SLD1_005 ←

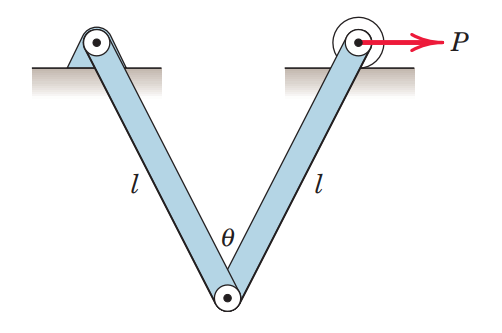
בפרקים קודמים חקרנו את השיווי משקל של גוף ע”י בידודו בעזרת דג”ח ומשוואות שיווי המשקל. ישנם גם בעיות בהן גופים יכולים לזוז ביחס אחד לשני, ובמצב זה יכולים להיות מספר מצבי שיווי משקל אפשריים. במצבים כאלו, כמו בפיזיקה, קל לנו יותר להשתמש בעקרונות אנרגיה ועבודה כדי למצוא פתרונות לבעיה הנתונה. שיטה זו נקראת שיטת העבודה הוירטואלית.

עבודה

עבודה של כוח

בפרק זה ניעזר במונחי העבודה והאנרגיה מפיזיקה. בעיקר:

ועבור העבודה הכוללת:

הערות:

1. נעסוק כעת רק בכוחות משמרים.

עבודה של מומנט טהור

בנוסף לעבודה הנעשית ע”י כוחות, מומנטים טהורים גם יכולים לבצע עבודה.

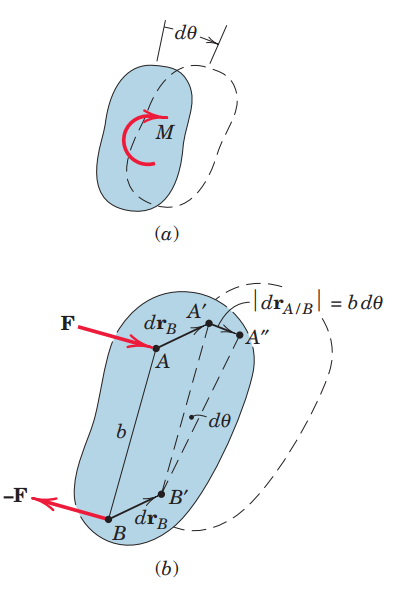
המומנט פועל על גוף ומשנה את המיקום הזוויתי שלו בגודל . העבודה הנעשית ע”י מומנט ניתנת לחישוב ע”י פירוק המומנט הטהור לשני כוחות שווים ומנוגדים בכיוונם ו- הפועלים בשתי נקודות ו- כך ש- (למה? תיזכרו במומנט טהור).

נפרק את הרוטציה הזאת לשני חלקים:

1. הזזה של הגוף
2. סיבוב סביב נקודה כלשהי שנסמן ב-.

בזמן שינוי אינפיטסימלי (מאוד קטן) במיקום הגוף, הקו זז למיקום החדש . נתייחס לההעתק של בשני שלבים - ראשית, העתק השווה לההעתק של . שנית, נתייחס לההעתק הנוצר כתוצאה מרוטציה סביב .

לכן העבודה הנעשית ע”י בזמן ההעתק מ- ל- שווה בגודל ומנוגדת בסימן לעבודה הנעשית ע”י בזמן ההעתק מ- ל-.
כלומר, בזמן ההזזה מ- ל-, לא התבצעה עבודה.
לעומת זאת, בזמן הרוטציה , כן מבצע עבודה:

כאשר . מאחר ו-, נוכל לרשום:

העבודה של מומנט היא חיובית אם פועל באותו הכיוון של השינוי , ושלילי אם פועל בכיוון הנגדי. העבודה הכוללת הנעשית ע”י מומנט טהור בזמן רוטציה סופית במישור המומנט נתונה ע”י:

עבודה וירטואלית

נעסוק כעת בחלקיק שהנקודת שיווי משקל שלו נקבעת ע”י כוחות שפועלים עליו. כל שינוי שרירותי קטן במיקום שלו הרחק ממקומו המקורי ובהתאם לאילוצי המערכת, נקרא העתק וירטואלי. במונח וירטואלי הכוונה לכך שהשינוי במיקום, ההעתק, לא באמת קיים, אלא אנו רק מניחים שהוא קיים כדי שנוכל להשוות בין מיקומי שיווי משקל שונים ונוכל להחליט על המיקום הנכון.
הכוח שנעשה ע”י כוח הפועל על חלקיק בזמן עבודה וירטואלית נקרא עבודה וירטואלית והוא נתון באופן הבא:

ההבדל בין ו- הוא ש- הוא שינוי אינפיטסימלי (מאוד קטן) אמיתי במיקום, ואלו לא.

שיווי משקל

נציג כעת את תנאי שיווי המשקל על חלקיק וגוף, בביטויים של עבודה וירטואלית.

שיווי משקל של חלקיק

נביט בחלקיק הבא הנתון תחת מספר כוחות:

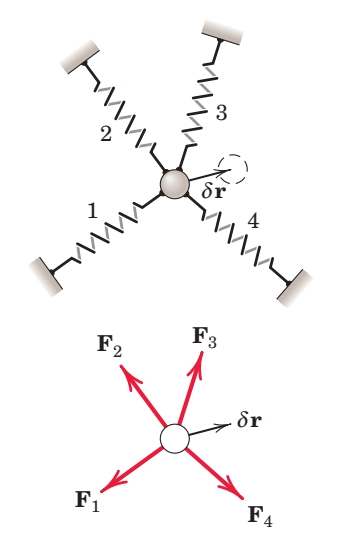
אם נזיז את החלקיק בהעתק וירטואלי כמו בשרטוט, אז העבודה הוירטואלית שלו נתונה ע”י:

אנו יודעים שבשיווי משקל ש-. מכך נסיק כי בשיווי משקל גם:

אנו בעצם אומרים שעבור חלקיק בשיווי משקל, העבודה של כל תזוזה קטנה שלו, שלא מפרה את אילוצי המערכת (כוחות, מומנטים) - מתאפסת.

בגדול, העיקרון של אפס עבודה וירטואלית של חלקיק יחיד לא מפשטת את הבעיה, כי המשוואות ו- נותנות לנו את אותה האינפורמציה. אנו מציגים את עיקרון זה כיוון שהוא כן עוזר כאשר אנו מרחיבים את הבעיה מחלקיק למערכת של יותר מסובכת של גופים קשיחים.

שיווי משקל של גוף

אם העבודה הוירטואלית של כל חלקיק בשיווי משקל מתאפסת, אז קל להסיק שעבור כלל גוף קשיח בשיווי משקל, גם העבודה הוירטואלית מתאפסת.
כאשר נחשב את , נשתמש רק בכוחות החיצוניים, הרי כל הכוחות הפנימיים מבטלים אחד את השני, והעבודה הכוללת שמתבצעת על ידם מתאפסת.

גם כאן המשוואה לא תורמת לנו. ניקח למשל את המערכת:

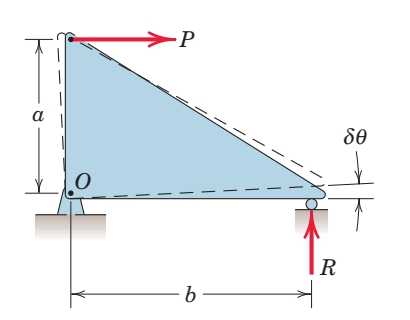
ננסה למצוא את , כאשר המערכת מועמסת בכוח ידוע . נניח כי מתבצע סיבוב קטן סביב הנקודה . העבודה המתבצעת ע”י היא . ע”י העבודה היא . מהעיקרון ש- נסיק כי:

אבל זה זה אותה המשוואה שהיינו מקבלים אם היינו מחשבים מומנט סביב הנקודה . גם פה לא הרווחנו שום דבר מהעיקרון של עבודה וירטואלית בשיווי משקל.

שיווי משקל של מערכות אידיאלית של גופים קשיחים

נעסוק כעת במערכות אידיאלית. מערכות אלו בנויות מ-2 או יותר גופים קשיחים המחוברים יחד ע”י חיבורים מכניים שלא מסוגלים לבלוע אנרגיה תחת מתיחה או לחיצה, ושהחיכוך קטן מספיק כך שנוכל להזניח אותו. דוגמה לכך היא המערכת הבאה:

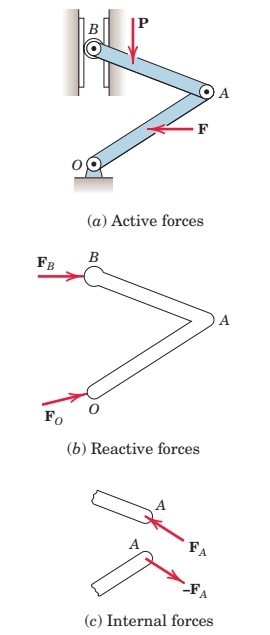
נסווג את הכוחות לשלושה קטגוריות:

1. כוחות מוכתבים הם כוחות המסוגלים לבצע עבודה וירטואלית תחת העתקים וירטואלים אפשריים. בשרטוט שלנו אלו כוחות ו-. הם כוחות מוכתבים כי הם יבצעו עבודה כאשר הקשרים יזוזו.
2. כוחות תגובה הם כוחות הפועלים בסמכים קבועים במקום כאשר שום העתק וירטואלית קורית בכיוון של הכוח. כוחות אלו לא פועלים תחת העתק וירטואלי. בשרטוט שלנו הכוח לא יכול לבצע עבודה כי שום תזוזה בכיוון הכוח שלו יכולה להתבצע. באותו אופן גם עבור הסמך הנייח בנקודה , התגובה לא יכולה לבצע עבודה, כי הנקודה לא יכולה לזוז.
3. כוחות פנימיים הם כוחות בקשרים בין האלמנטים/מוטות. תחת כל תזוזה במערכת, הכוח השקול (הכולל) המתבצע ע”י הכוחות הפנימיים הוא תמיד אפס. הסיבה לכך היא שהכוחות הפנימיים תמיד מגיעים בזוגות של כוחות שווים ומנוגדים בכיוונם. בשרטוט ניתן לראות זאת בכוחות ו-.

עיקרון העבודה הוירטואלית

שמנו לב כי הכוחות המוכתבים הם היחידים שמבצעים עבודה וירטואלית במערכת. נוכל כעת לומר את המשפט הבא:

משפט:

העבודה הוירטואלית המתבצעת ע”י כוחות מוכתבים במערכת מכנית אידיאלית בשיווי משקל היא אפס לכל ההעתקים (שינויים) וירטואליים שלא מפרים את אילוצי המערכת.

כאשר באילוצי המערכת הכוונה בהגבלת התנועה ע”י הסמכים.

כאשר אנו משתמשים בעיקרון זה, אין לנו צורך לשרטט דג”ח מלא של המערכת, אלא רק להתייחס לכוחות המוכתבים. בשרטוט הקודם, נתחייס רק ל-.

דרגות חופש

מספר דרגות החופש של מערכת מכנית היא מספר הסקלרים המינימליים שדרושה כדי לתאר באופן מלא את המערכת.

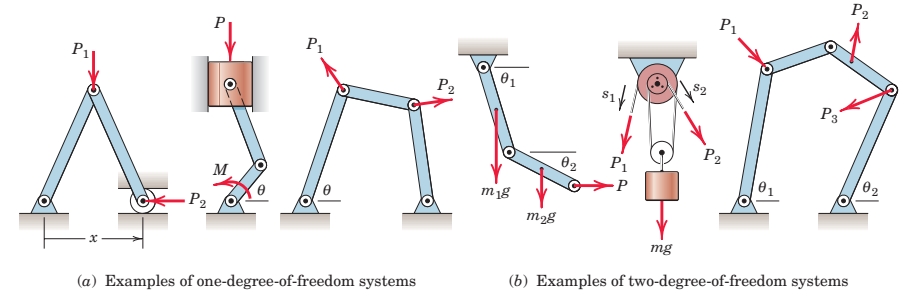
נפעיל עיקרון העבודה הוירטואלית כמספר דרגות החופש במערכת. בכל פעם, ניתן רק לדרגת חופש אחת לנוע וירטואלית כאשר משאירים את שאר דרגות החופש קבועים.

דוגמאות:

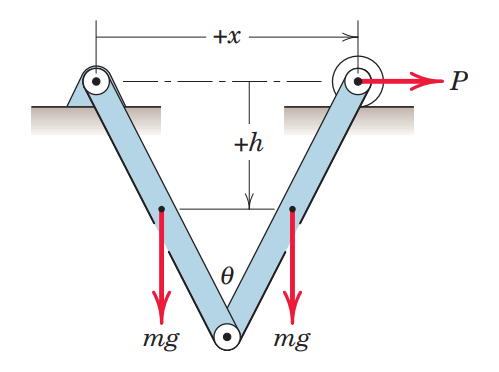
1. כל אחד מהמוטות באיור הבא בעלי מסה ואורך , כאשר הם נתמכים ע”י הסמכים הנתונים. עבור כוח , מצאו את הזווית עבורה ישנה שיווי משקל.
   
   פתרון:
   הכוחות המוכתבים הם כוח הכבידה הפועל על שני המוטות והכוח . כל שאר הכוחות הם כוחות תגובה וכוחות פנימיים ולכן הם לא מבצעים עבודה.
   לפי עיקרון העבודה הוירטואלית, כלל העבודה של כלל הכוחות המוכתבים היא אפס לכל הזזה וירטואלית תחת אילוצי המערכת. נסמן את השינויים הוירטואליים במערכת ונקבל כי:

שימו לב כי בחרנו את הכיוונים החיוביים של ו- בכיוון הכוחות שמבצעים עבודה לאורכם.
נציג את השינויים ב- ו- ע”י המשתנה . מגאומטרייה פשוטה:

השינוי כתגובה לשינוי , היא גזירה של משוואה זו:

זוהי לא גזירה לפי ! לכן לא קיבלנו מהירות באגף שמאל, אלא ביטוי המתאר כמה משתנה כאשר אנו משנים את ב-.
באותו אופן, עבור :

נציב בחזרה ב-(1):

ונקבל:

תרגילים:

1. נתון:
   
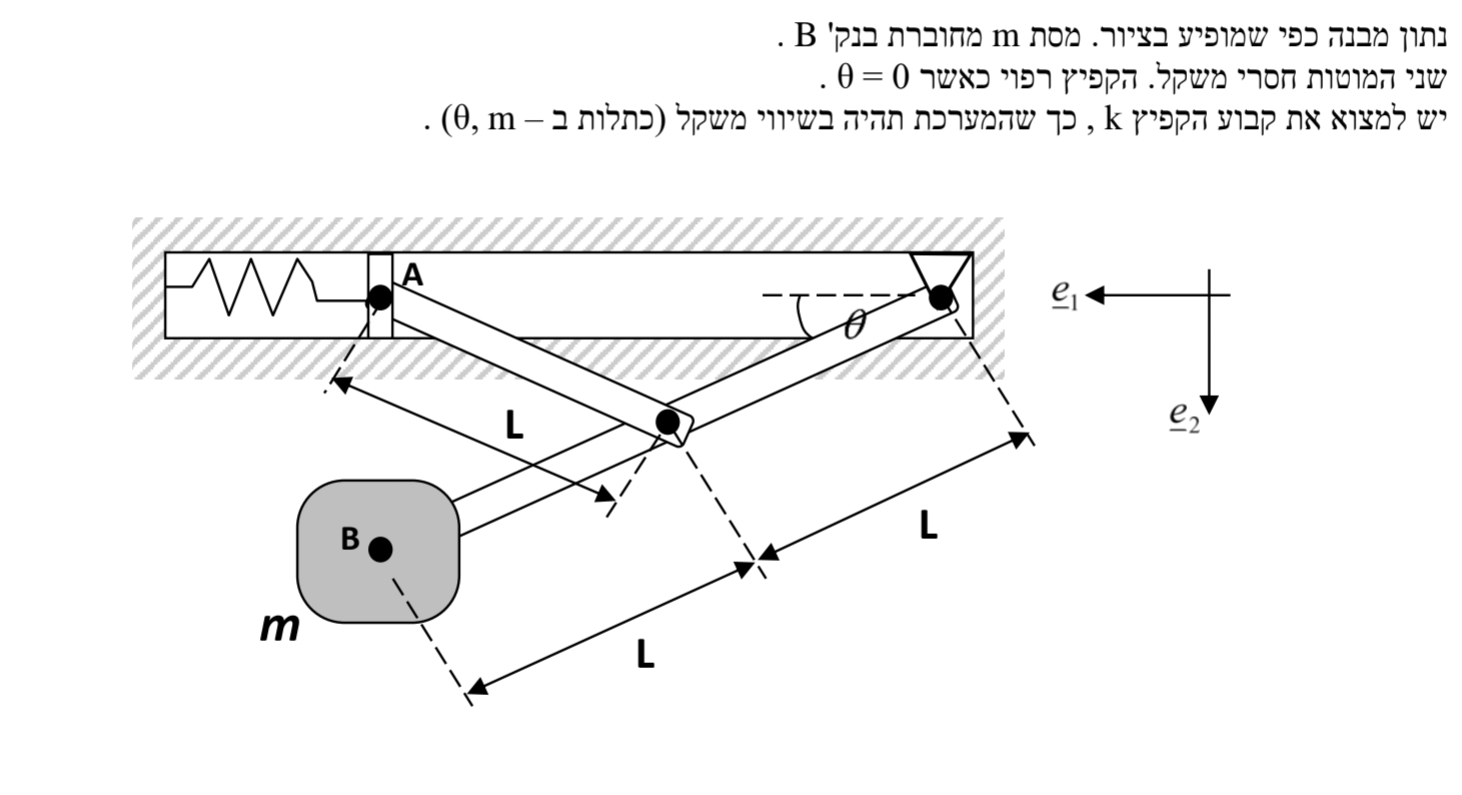
   פתרון:
   נשרטט דג”ח:
   
   יש לנו דרגת חופש אחת, , ושני כוחות .
   נמצא את תלות ב-: נמצא את התלות של (השינוי במרחק הקפיץ ממצבו הרפוי) ב-: נגזור כדי לקבל את השינוי: כעת לפי עיקרון העבודה הוירטואלית:
2. נתון:
   
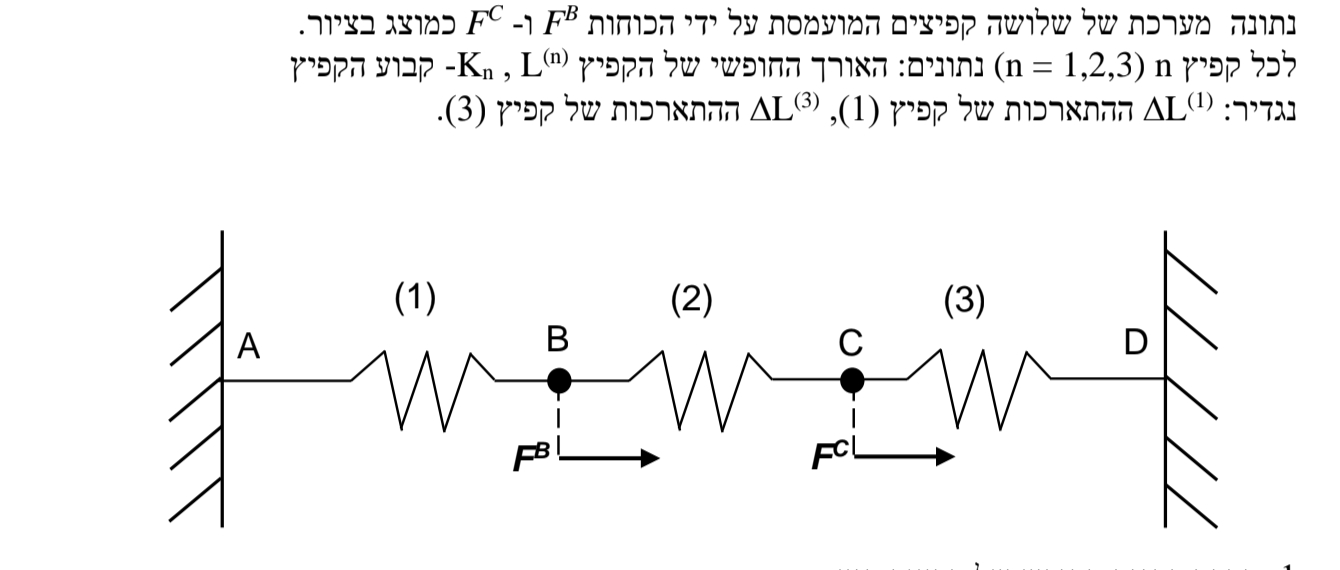
   מצאו את העבודה הוירטואלית שנעשית ע”י כלל הכוחות.
   פתרון:
   נשים לב שסכום התארכות הקפיצים תמיד מתאפסת כי האורך הכולל לא יכל לגלוש מעבר לאורך :
   
   נסדר, ונקבל את שתי דרגות החופש שלנו :
   
   יש לנו את הכוחות:
   
   נבחר כהנקודת ייחוס שלנו:
   
   נגזור:
   
   לפע עיקרון העבודה הוירטואלית:
   

→ קודם: SLD1_003הבא: SLD1_005 ←