DYN1_006 קינטיקה של מערכת חלקיקים

→ קודם: DYN1_005הבא: DYN1_007 ←

תנע קווי של מערכת חלקיקים

עבור מערכת של חלקיקים עם וקטורי מיקום ומסות , נוכל לסווג את הכוחות הפועלים עליהם לשתיים:

1. סכום כוחות חיצוניים .
2. סכום כוחות פנימיים כוח על חלקיק המופעל ע”י חלקיק . כמובן שמחוק שלישי של ניוטון, מתקיים .

נסיק שלפי חוק שני של ניוטון, עבור חלקיק :

אם נגדיר תנע קווי של חלקיק בצורה , נוכל לרשום:

נסכום כעת את משוואה זו על פני כל מערכת החלקיקים :

נשים לב שהסכום הכפול מתאפס, כי בעצם כל נסכם פעמיים - פעם בסימן חיובי ופעם בסימן שלילי (הם כוחות פנימיים).
נגדיר גם תנע קווי כולל, סכום כוחות חיצוניים כולל של המערכת:

נציב בחזרה ונקבל:

שזהו מאזן תנע קווי עבור מערכת של חלקיקים.

נגדיר מסה כוללת:

ואת מרכז המסה:

זהו וקטור שתלוי בזמן, ולכן יש לו גם מהירות:

ולכן התנע הקווי שלו:

נקבל למעשה שהתנע הקווי של מרכז המסה (עם המסה הכוללת) הוא התנע הקווי של מערכת החלקיקים:

ולכן מאזן תנע קווי של מערכת חלקיקים הוא:

כאשר .

תנע זוויתי של מערכת חלקיקים

תנע זוויתי מוחלט

משוואת התנע זוויתי של חלקיק יחסית לנקודה הקבועה היא:

נגדיר תנ”ז כולל מוחלט:

נרצה למצוא מאזן תנ”ז מוחלט כולל של המערכת חלקיקים.

מאזן התנ”ז המוחלט לחלקיק :

כאשר .
אם נסכום את משוואה זו על , נקבל:

נשתמש ב- , ונקבל:

אנו יודעים ממוצקים 1 שכוח מכוון בכיוון הקו המחבר מאפס את המומנט:

נישאר עם:

נגדיר כסכום המומנט של הכוחות החיצוניים בלבד, ביחס ל-. נקבל את המאזן תנע זוויתי מוחלט במערכת חלקיקים:

תנע זוויתי יחסי

תהי נקודה נעה כלשהי . משוואה התנע הזוויתי של חלקיק ביחס לנקודה היא:

נגדיר תנ”ז יחסי כולל:

ונגדיר מומנט כולל של כוחות חיצוניים בלבד ביחס ל-:

נפתח את ונקבל:

נגזור בזמן ונקבל:

ונקבל את מאזן התנ”ז היחסי למערכת חלקיקים:

מקרים פרטיים לבחירת :

1. אם היא נקודה עומדת, שתיקרא , נקבל , ונחזור למאזן תנע זוויתי מוחלט:
2. אם נעה עם מרכז המסה, מתקיים , ואז , כך ש: וזהו מאזן תנע זוויתי ביחס למרכז המסה.
3. מקרה נדיר נוסף בו הוא כאשר הנקודה מאיצה רגעית לכיוון מרכז המסה:

עבודה ואנרגיה במערכת חלקיקים

את הגדלים נוכל להגדיר עבור מערכת חלקיקים כסכום הגדלים המתאימים להם של כל חלקיק במערכת:

ועדיין יתקיים:

נתבונן במאזן ההספקים הכללי:

קיבלנו ביטוי ל-:

הכוח הפנימי הוא בכיוון הקו המחבר ולכן איבר של הכוח הפנימי פרופורציוני ל- . אם החלקיקים מחוברים באופן קשיח () אזי , כלומר הכוח הפנימי אינו מבצע עבודה.
לעומת זאת, אם המרחק לא קבוע, אז מבצע עבודה.

נפתח את הביטוי לאנרגיה קינטית כוללת:

נשתמש במהירות מרכז המסה, ונרשם , כך ש:

נשים לב שמתקיים:

נציב בחזרה ונקבל:

קיבלנו:

הכוח הכללי (חיצוני או פנימי) הינו משמר אם לכל מסלול סגור. נוכל להגדיר עבורו אנרגיה פוטנציאלית :

נציב בחזרה בביטוי ל-, ולאחר אלגברה, נקבל כי מאזן ההספקים והאנרגיה עדיין תקפים באותה הצורה למערכת חלקיקים:

דוגמה: 2 חלקיקים מחוברים בקפיץ

נתונים שני חלקיקים במסות , כך ש- . הם מחוברים בקפיץ עם אורך רפוי וקשיחות . כוח הכבידה לא זניח. נסמן את המרחק בין שני הגופים ב-.
נתונים תנאי התחלה:

נדרש למצוא את תנועת מערכת החלקיקים.

ניתן לראות כי מרכז המסה של המערכת נמצא תמיד במרחק מ-:

נסמן את את הכיוון היחסי של ביחס ל- ב-, כך ש:

ולכן המיקומים של שתי המסות הן:

נבצע גם מאזן תנע זוויתי וגם מאזן אנרגיה.
ממאזן תנע זוויתי ביחס למרכז המסה:

במומנט יושבים רק הכוחות החיצוניים:

במקרה שלנו רק . למעשה, סכום כוחות הכבידה פועל ממרכז המסה של המערכת - כי מרכז הכובד ומרכז המסה מתלכדים. לפיכך, נסיק שצד ימין של המשוואה מתאפס:

יש לנו שימור תנ”ז יחסי:

נפתח את :

אנו יודעים כי . נוכל להגדיר וקטור מהירות זוויתית כך שמתקיים (כי וקטור כיוון). לפיכך:

נחשב כל מכפלה וקטורית בנפרד:

ולכן:

אנו מצאנו כי . נסמן , ונסיק כי:

לכן:

נרצה למצוא את .
כיוון שמדובר במקרה מישורי, נוכל להשתמש במציאת רכיב נורמלי של המהירות הזוויתית, שגם נכון עבור 2 חלקיקים כלליים:

במקרה שלנו:

ממאזן אנרגיה נקבל:

אין כוחות בלתי משמרים (יש רק כוח כבידה וקפיץ) ולכן . לפיכך:

האנרגיה הפוטנציאלית של הקפיץ והכבידה:

למעשה, במערכת חלקיקים, נוכל להיעזר במרכז מסה ולקבוע כי אנרגיית הכבידה היא:

האנרגיה הקינטית:

נשים לב כי:

נציב בביטוי ל-:

נציב את במאזן אנרגיה:

נוכל לטעון גם ש- . לכן:

כך ש:

נוכל להציב את (1), ונישאר עם ביטוי שכולל רק את ו-. לאחר אלגברה, נקבל ביטוי מהצורה:

מתקף והתנגשות במערכת חלקיקים

עבור חלקיק בודד , המתקף קווי:

והמתקף זוויתי:

עבור חלקיק שנמצא כחלק ממערכת חלקיקים, נצטרך גם לקחת בחשבון כוחות פנימיים :

עבור כלל המערכת:

באותו אופן:

עבור התנגשות בין שני חלקיקים , מתקף הכוח מקיים .
את זמן ההתנגשות נסמן ב-. עבור המהירויות:

ולכן:

עבור המקרה הפשוט של שני חלקיקים , בו אין כוח חיצוני:

עבור חלקיק :

עבור חלקיק :

נסכום את שתי המשוואות, מתבטל, ונקבל:

שזה פשוט התנגשות של שני חלקיקים מפיזיקה 1.
באופן כללי, בסכימה של המתקפים על , כאשר לא פועלים כוחות חיצוניים, מקבלים כי יש שימור תנע קווי כולל:

אבל, שימור תנע קווי כולל עדיין לא מספיק לנו כדי למצוא פתרון ל-. צריכים הנחות נוספות.

• אפשרות א’ - ההתנגשות פלסטית לחלוטין: נציב בחזרה בשימור תנע קווי: נשים לב שמופיע כאן הגדרת מרכז המסה, ולכן:
• אפשרות ב’ - התנגשות חסרת חיכוך עם מקדם תקומה:
  
  נגדיר וקטור נורמל בכיוון מ- אל . מתקף הכוח הפנימי פועל בכיוון בלבד: נצטרך עוד משוואה - קשר מהירויות יחסיות בכיוון ע”פ מקדם תקומה:

  הערה: ) שבהם ניתן להזניח את השפעת כל הכוחות הסופיים שפועלים על מערכת של שני החלקיקים ולהתייחס אך ורק לכוחות המתקף שפועלים ביניהם בעת ההתנגשות וגורמים לשינוי בתנע הקווי שלהן.

  מתקף בין חלקיקים מניח פרקי זמן מאוד קצרים (כלומר כש-

תרגילים

שאלה 1

בקצות עגלה הנמצאת במנוחה, עומדים שני אנשים. בזמן הם מתחילים לנוע אחד לקראת השני. אין חיכוך בין גלגלי העגלה לרצפה.

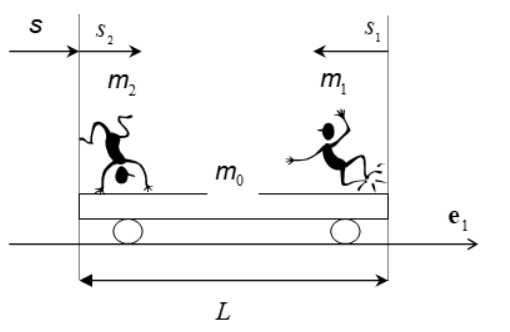
סכימת העגלה

נתונים הגדלים: מסת העגלה; מסות האנשים; אורך העגלה; - קואורדינטות המתארות את מיקום האנשים ביחס לקצות העגלה; קואורדינטה המתארת את מיקום העגלה ביחס לראשית.
בנוסף, נתונים תנאי ההתחלה:

סעיף א’

מהו מרחק העגלה מהראשית , כאשר ו- נפגשים (הביעו כתלות ב- כאשר הינו הרגע בו הם נפגשים)?

פתרון:
נשתמש במאזן תנע קווי:

נמצא את הכוחות:

דג”ח על העגלה והאנשים

משקול כוחות:

אנו יודעים כי אין תאוצה בכיוון , ולכן נוכל לומר ש- .
נסיק כי ישנו שימור תנע קווי בכיוונים .

לפי מאזן תנע קווי:

מאחר ו- , נסיק כי , ולפיכך:

כיוון שהעגלה במנוחה, אנו יודעים כי בכל זמן :

ולכן גם:

כלומר:

מהגדרת מרכז מסה:

נציב (כלומר, את תנאי ההתחלה):

נציב ב- , ונקבל לאחר אלגברה ש:

נותר לנו למצוא את . עבור הזמן בו הם נפגשים, מתקיים:

נציב ונקבל:

סעיף ב’

מהי מהירות העגלה כתלות ב-?

פתרון:
נגזור את הפתרון הקודם ונקבל:

שאלה 2

שתי מסות מחוברות באמצעות קפיץ דרוך (הקפיץ בעל מסה זניחה ואורך רפוי ) באורך , ונעות על גבי שולחן חלק, תוך שהן סובבות במהירות זוויתית . מהירות מרכז המסה של המערכת הינה:

בנוסף, הינה קואורדינטה המציינת אורך הקפיץ.
ברגע משוחרר הקפיץ () וברגע שתי המסות מתנתקות מהקפיץ כאשר הוא מגיע לאורכו הרפוי .
נתונים הגדלים .

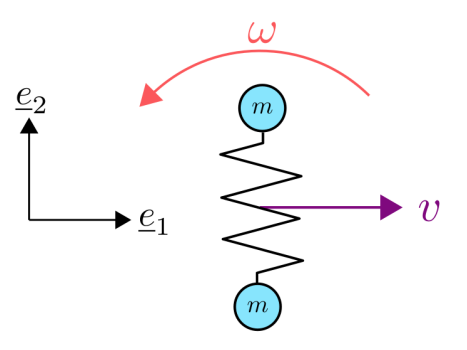
פתרו את הסעיפים הבאים כתלות בפרמטרים הנתונים:

סעיף א’

חשבו את התנע הקווי הכולל ואת התנע הזוויתי סביב מרכז המסה לפני שחרור הקפיץ.
הדרכה: מצאו קודם את הגדלים במערכת כתלות ב- ובמהירות הזוויתית של המערכת ולאחר מכן הציבו ערכים מתאימים עבור .

פתרון:
נגדיר מערכת צירים סובבת:

מעצם הגדרת המערכת צירים והנתונים:

המיקומים היחסיים:

לאחר כלל האופרטור:

לא פועלים כוחות חיצוניים בכיוונים ו-, או מומנטים חיצוניים בכיוון , ולכן נשמר בהם התנע הקווי והזוויתי. לכן, קבוע לכל , כך שהוא תמיד . כלומר:

לכן סך התנע הקווי (לפי הגדרה):

לכן לפני שחרור הקפיץ:

מבחינת תנע זוויתי סביב מרכז המסה (לפי הגדרה):

נקבל כי ברגע :

סעיף ב’

חשבו את התנע הקווי הכולל ואת התנע הזוויתי סביב מרכז המסה ברגע .

פתרון:
עבור , נישאר עם אותו הגודל, כי התנע הקווי והתנע הזוויתי נשמרים:

סעיף ג’

מצאו את גודל המהירות הזוויתית של הקפיץ ברגע .

פתרון:
אנו יודעים שהמהירות הזוויתית נשמרת, ולכן:

נציב בביטוי שמצאנו ל-:

סעיף ד’

חשבו את האנרגיה המכנית של המערכת כתלות ב- ו- ובמהירות הזוויתית של המערכת.

פתרון:
אנרגיה מכנית מוגדרת כ-. לכן, במקרה שלנו:

ולכן:

סעיף ה’

מהי המהירות היחסית בין המסות לאחר שחרור הקפיץ?

פתרון:

ב-:

נשתמש בשימור אנרגיה למציאת . אנו יודעים שיש שימור אנרגיה כי הכוחות הלא משמרים לא מבצעים עבודה (גם פנימיים וגם חיצוניים):

נציב לפי סעיף קודם:

נקבל לאחר אלגברה:

נציב בביטוי ל-:

שאלה 3

חלקיק בעל מסה ומהירות אשר הינה בזווית ביחס ל- וגודלה , מתנגש ברכב בעל מסה המצוי במנוחה. הרכב יכל לנוע בכיוון בלבד. מקדם התקומה בין הגופים הוא .

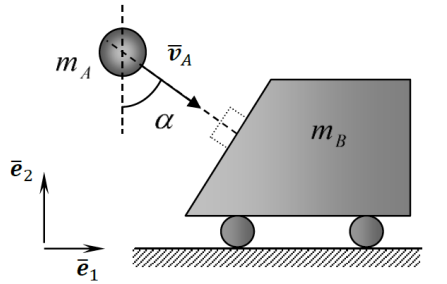
סכימת העגלה

נתונים .

סעיף א’

חשבו את מהירות הרכב ומהירות החלקיק מיד לאחר ההתנגשות בהנחה שאין חיכוך בינהם בזמן ההתנגשות.

פתרון:

נרצה להשתמש במקדם התקמוה כדי לחשב את המהירויות לפני ההתנגשות:

הוקטורים המשיקים והניצבים להתנגשות

נשים לב כי . מהגדרת מקדם התקומה:

נשים לב כי:

ולכן:

נוכל לחלץ עוד מידע מהמתקף:

דג”ח על כל אחד מרכיבי המערכת

נוכל לחשב את המתקף על החלקיק בפרק זמן ההתנגשות, (רגעי):

הגודל הוא גודל חסום, ולכן הוא ייתאפס. לעומת זאת, הוא לא חסום, ולכן נקבל שתוצאת האינטגרל הוא ערך סופי:

מבחינת שינוי התנע:

ממאזן מתקף, אנו יודעים ש:

נציב בשני צידי המשוואה:

מאחר ויש לנו רק וקטורים בכיוון , עם נעלם אחד, נסיק כי הוא רק בכיוון , ולכן:

מבחינת כוחות חיצוניים, על כל המערכת:

לפיכך, אין כוחות בכיוון . כלומר, מתקיים שימור תנע קווי בכיוון זה:

כלומר, התנע לפני ההתנגשות שווה לתנע אחרי ההתנגשות. נקבל:

מ-(1) ו-(2) ונקבל:

סעיף ב’

חשבו את המתקף של הכוח הנורמלי מהרצפה במהלך ההתנגשות.

פתרון:

ראינו כבר כי מבחינת כוחות חיצוניים, על כל המערכת:

לפיכך, המתקף:

הכבידה הינה כוח חסום, והנורמל הינו כוח ריאקטיבי, כך ש:

נחשב את השינוי בתנע (של כל המערכת):

נשווה לפי מאזן מתקפים ונקבל:

→ קודם: DYN1_005הבא: DYN1_007 ←