פנגייה

DYN1_008 טנזור האינרציה

• זמן קריאה: 17 דק'

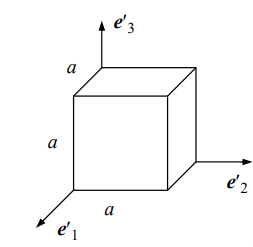
טנזור האינרציה

כבר ראינו ש:

כמו במאזן תנע זוויתי מישורי, נרצה למצוא ביטוי יותר נוח לתנע זוויתי, הפעם במקרה המרחבי.

מהגדרה, התנע הזוויתי ביחס לנקודה נעה :

מאחר ו- היא נקודת צמודת גוף, נוכל להשתמש בקשרי גוף קשיח:

נציב:

נשתמש ב-bac to cab:

נעבור לסימון וקטורי-מטריצי. כלומר, נרשום את כוקטורי עמודה:

נוציא את לצד ימין, ונוכל לרשום מחדש את התנ”ז, בצורה הבאה:

כדאי לנסות לעבור מכתיב מטריצי זה לכתיב הקודם כדי לראות מה באמת קרה כאן.

קיבלנו מטריצה באינטגרל. את מטריצה זו נגדיר:

הגדרה:

טנזור האינרציה מוגדר כהאינטרל הבא:

כאשר הוא מטרציה היחידה.

בכתיב אינדקסי:

אז למשל:

הערות:

  1. נשים לב שכעת, לעומת המקרה המישורי, יש חשיבות לאוריינטציה של מערכת הצירים שלנו. כלומר, אם נסובב את מערכת הצירים שלנו, נקבל טנזור אינרציה שונה.
  2. עבור מערכת צירים צמודת גוף , המטריצה תהיה קבועה. לכן, אפשר לומר כי טנזור האינרציה הוא תכונה של הגוף.
  3. עבור גוף עם צפיפות אחידה, האינטגרל בטנזור האינרציה הופך להיות פשוט אינטגרל על הנפח, כך שטנזור האינרציה הופך להיות תכונה גאומטרית.
  4. הצבה זריזה מראה שטנזור האינרציה סימטרי.

דוגמה: תיבה מלבנית בהינתן תיבה מלבנית אחידה, נחשב את טנזור האינרציה ביחס למרכז המסה, במערכת צירים המקבילים לצלעות התיבה. נקבל (ביחס למרכז המסה):

בנוסף, כיוון שהגוף סימטרי:

דוגמה: גליל מלא


ביחס למרכז המסה:

כיוון שהגוף סימטרי:

דוגמה: כדור מלא


הגוף סימטרי סביב כל ציר שעובר במרכז המסה, כך שנקבל טנזור הידרוסטטי/איזוטרופי/איך שתרצו להקביל למקרים דומים:

דוגמה: כדור חלול עבה דופן


באותו אופן כמו בכדור מלא, נקבל גם כן טנזור אלכסוני:

דוגמה: כדור חלול דק דופן


נוכל פשוט להשאיף את הביטוי שקיבלנו בכדור חלול עבה דופן, למקרה בו . לאחר קצת לופיטל, נקבל:

תנע זוויתי יחסי של גק”ש במרחב

לכן, התנ”ז היחסי לנקודה :

בכתיב אינדקסי:

משפט ההזזה המקבילה

נוכל להכליל את משפט שטיינר למקרה המרחבי - הזזה של נקודת הייחוס לחישוב טנזור אינרציה.

משפט:

בהינתן טנזור ביחס למרכז המסה , טנזור האינרציה ביחס לנקודה הוא:

בכתיב אינדקסי, למשל:

או אם :

פיתוח:
נתון , ונרצה לחשב את .
מהגדרה:

נציב :

דוגמה: כדור מלא


אנו יודעים שביחס למרכז המסה:

נרצה להזיז את נקודת הייחס של טנזור האינרציה לנקודת שפה , שנמצאת ביחס למרכז המסה ב:

לפי משפט ההזזה המקבילה:

נציב במשפט את :

נקבל:

טרנספורמציית סיבוב

אנו יודעים שהקשר נכון בכל מערכת צירים (כל עוד שלושת האיברים באותה המערכת צירים).
כלומר, שני הביטויים הבאים נכונים:

בהינתן , נרצה למצוא ביטוי ל-, כי יכל להיות שיותר נוח לנו לעבוד במערכת צירים .
נסמן מטריצת סיבוב הממירה ממערכת צירים ל-. לכן:

הערה:

שימו לב ש- הם וקטורים, בעוד הם מטריצות!

אבל, כיוון ש- , נוכל פשוט להסיק כי:

עבור טנזור אינרציה לא אלכסוני, הוקטורים , , הם לא בהכרח באותו הכיוון. אם טנזור האינרציה כן אלכסוני, אז ו- כן באותו הכיוון, והרבה יותר נוח לנו לתאר את המערכת.
האם תמיד קיימת טרנספורמציה שהופכת את טנזור האינרציה לאלכסונית? כלומר, האם לכסינה?
כן! לא נוכיח, אבל זה זהה לגמרי למציאת מאמצים ראשיים בבמוצקים 2.

הע”ע של נקראים מומנטי האינרציה הראשיים, והוקטורים העצמיים הם צירי האינרציה הראשיים אשר בונים את טנזור הטרנספורמציה :

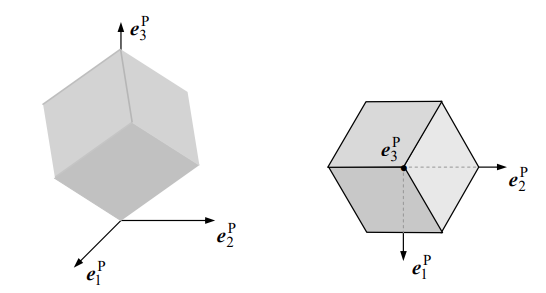
דוגמה: קוביה מלאה

לקוח מתוך (Elata, 2002).
book
חשבו את טנזור האינרציה של הקובייה המסתובבת סביב נקודת הראשית, ומצא את הערכים והכיוונים הראשיים.

פתרון:
במערכת הראשית העוברת במרכז המסה, אנו יודעים ש:

היות ושלושת הערכים העצמיים זהים, הטנזור הוא טנזור איזוטרופי (כל מערכת העוברת במרכז המסה היא מערכת ראשית). במערכת המקבילה, יחסית לראשית נקבל:

הערכים העצמיים של הטנזור הם:

והוקטורים העצמיים המתאימים הם:

הערך העצמי שווה לערך העצמי סביב מרכז המסה מכיוון שהוקטור הראשי התואם עובר דרך מרכז המסה.

רכיבי טנזור הטרנספורמציה מהמערכת המתוארת למערכת הראשית היא:

book

מאזן תנע זוויתי יחסי במערכת צירים צמודת גוף

ביחס לנקודה נעה , אנו יודעים ש:

עבור נקודת צמודת גוף , ראינו במקרה המרחבי כי:

נוכל לבטא זאת במערכת צירים צמודת גוף . במקרה זה, היא מטריצה של גדלים קבועים. לכן, כאשר נגזור את הביטוי:

ממאזן תנע זוויתי יחסי:

נשווה בינהם ונקבל:

מקרים פרטיים:

  • עבור נקודת ייחוס במרכז המסה:

  • אם לגוף יש נקודת ייחוס נייחת:

  • אם מכוון בכיוון ציר אינרציה ראשי וגם המומנט בכיוון זה , נקבל:

דוגמה: כדור על דסקה סובבת



כדור במסה ורדיוס מתגלגל ללא החלקה על דסקה המסתובבת במהירות זוויתית קבועה .
מיקום מרכז המסה על הכדור נתון ע”י:

מקנים לכדור תנאי התחלה . דרוש למצוא את מסלול התנועה ואת , שהיא המהירות הזוויתית של הכדור.

לפי מאזן תנע קווי:

לפי מאזן תנע זוויתי ביחס למרכז המסה:

מהדג”ח, אנו יודעים ש:

אנו גם יודעים שבמקרה של כדור:

נציב במאזן התנע הזוויתי:

נבודד את ב-(1), ונציב לתוך (2) ונקבל:

ברכיבים:

קיבלנו כי בכיוון , . כלומר, הסיבוב ההתחלתי של הכדור סביב לא משתנה.

עבור שאר הכיוונים, ניעזר כבר בתנאי אי-החלקה (גלגול טהור) - . עבור הנקודה על הכדור:

נקודה על הדסקה:

נשווה בין ו- ונפרק לכיוונים:

נרצה לשלב את משוואות אלו עם משוואות (3). כדי לעשות זאת, נגזור קודם את משוואות אלו, כאשר נשים לב ש- :

נציב את (3) לתוך (5) (נבטל את ):

נזהה שזוג משוואות אלו הן למעשה נגזרות של משוואות יותר פשוטות:

לכן, נוכל לומר כי:

נציב את מ-(7b) לתוך (6a):

כאשר . נגדיר משתנה . לכן:

הפתרון של משוואה דיפרנציאלית זו היא:

נוכל לחזור למשתנה :

כאשר נקבעים ע”י תנאי ההתחלה.
באותו אופן נבצע עבור , ונקבל:

כאשר , ו- נקבעים ע”י תנאי התחלה.

משוואות אויילר

ראינו במאזן תנע זוויתי ש:

נוכל לבחור מערכת צירים צמודת גוף של צירי אינרציה ראשיים:

לכן:

כאשר . נוכל להציב במאזן כדי לקבל:

משוואות אלו נקראות משוואות אויילר לגוף קשיח.

  • אם ו-, אז:

    ואז נוכל להסתפק במשוואה אחת כדי לתאר את סיבוב הגוף:

  • עבור תנאי התחלה שאינו חד-צירי במדויק:

    כאשר .
    נציב במשוואות אויילר ונקבל ש- , אבל גם . כלומר, העובדה שיש סיבוב קטן ב-, גורם לכך שרגע אחרי יהיה סיבוב גם ב- - יש צימוד בין הצירים הצמודי גוף.

  • מקרה נוסף מעניין הוא גוף עם סימטריה סיבובית (אקסיסימטרי). למשל, עבור גליל, . ממשוואת אויילר בכיוון , נקבל:

    מה שמבטל את הצימוד בין הצירים ו-, וגם את הצימוד בין הצירים ו-.

מתקף והתנגשות בגק”ש

התנגשות של גוף קשיח כללי בקיר. כוח ההתנגשות לא חייב להיות נורמלי לקיר.

במקרה של התנגשות בנקודה , נוכל להגדיר מקדם תקומה:

כאשר .

כמו במערכת חלקיקים, נוכל לפתח מאזן מתקף קווי:

כאשר . באותו אופן, מאזן מתקף זוויתי:

את השינוי בתנע הזוויתי נוכל לרשום בעזרת טנזור אינרציה:

ואז:

המתקף מכיל מתקף בלתי חסום של ההתנגשות עצמה בנקודה . כלומר:

לכן, מהגדרת המומנט, נוכל לרשום את המתקף הזוויתי באופן הבא:

נדרש להניח הנחה נוספת בכיוון המשיקי למגע, . ישנם שני סוגי הנחות שניתקל בהן:

  • אפשרות א’ - מגע חסר חיכוך, ואז המתקף הוא רק בכיוון הנורמלי - .
  • אפשרות ב’ - אי-החלקה לאחר ההתנגשות - .

עבודה ואנרגיה בגק”ש

הספק מכני

במערכת חלקיקים ראינו כי אם הגוף קשיח, ההספק יהיה תלוי אך ורק בכוחות החיצוניים:

נשים לב שעל גוף קשיח יכל לפעול גם מומנט טהור . כדי לחשב את ההספק שלו, נוכל להחליף את המומנט הטהור בצמד כוחות הפועלים בשתי נקודות :

כך ש- . הספק שני כוחות אלו:

אם נקודות צמודות גוף, אז . נקבל שההספק של שני הכוחות הוא:

לכן, נסיק כי במקרה של גוף קשיח:

כאשר הוא נקודת הפעלת הכוח, ואנו גם מבצעים אינטגרציה על ההספק של כל אלמנט .

נרשום מחדש את משוואה זו, הפעם ביחס לנקודת מרכז המסה :

מקשרי גוף קשיח:

נרצה להוציא את מהסכימה והאינטגרל (בעזרת ציקליות של מכפלה מעורבת):

נוציא את ו-:

הביטויים בתוך הסוגריים הם פשוט הביטויים לסך הכוחות והמומנטים הפועלים על גק”ש ביחס למרכז המסה שלהם:

אנרגיה קינטית בגק”ש מרחבי

בפרק קודם עסקנו באנרגיה קינטית במקרה המישורי. כעת בעזרת הגדרת טנזור האינרציה נוכל להרחיב למקרה המרחבי. ראינו כי ביחס לנקודה צמודת גוף :

מהגדרת טנזור האינרציה אנו יכולים לרשום , ולכן:

את המכפלה הסקלרית ניתן גם לרשום באופן הבא:

זוהי מכפלה של שורה, במטריצה, בעמודה, מה שמניב סקלר. נקבל:

אם ו- מבוטאים במערכת צירי אינרציה ראשיים, אז בכתיב אינדקסי:

ואז מתקיים:

ואז:

אם נבחר נקודת ייחוס במרכז המסה, במערכת צירים ראשית:

אם לגוף הקשיח יש נקודה עומדת , אז במערכת צירים ראשית:

אם נרצה לגזור את עם נקודת ייחוס במרכז המסה:

נשים לב שלפי מאזן תנע קווי מתקיים . בנוסף, נוכל לבטא את הביטוי השני בעזרת מומנט סביב (לפי מאזן תנע זוויתי):

נציב בנגזרת של :

קיבלנו את הביטוי להספק מכני:

כעת, כמו בחלקיק, נוכל לקבוע כי עבור גוף קשיח ישנו מאזן אנרגיה כללי ומאזן הספקים כללי:

דוגמה: מטוטלת על בסיס נע

נתונה מטוטלת הנעה על בסיס חסר מסה, שנע ללא חיכוך על מסילה. למפרק מחובר מוט אחיד ודק בעל מסה ואורך .

משחררים את המטוטלת ממנוחה במצב:

נדרש למצוא את תנועת המטוטלת.

נוכל לומר כי יש שימור אנרגיה מכנית כוללת, כי כל הכוחות במערכת שמבצעים עבודה הם כוחות משמרים.

מהדג”ח ניתן לראות שיש שימור תנע קווי בכיוון (אין כוחות הפועלים בכיוון זה).

אנחנו גם יודעים שבהתחלה (המטוטלת שוחררה ממנוחה). לכן, מהשימור:

לכן, נוכל לומר ש:

ולכן בכל רגע מיקום מרכז המסה בכיוון נשאר במיקומו ההתחלתי:

בהמשך נראה כי הוא פשוט:

מיקום מרכז המסה הוא:

נגזור:

מצאנו ש- , ולכן:

נרצה להשתמש בשימור אנרגיה, אז נחשב את האנרגיה הקינטית:

במקרה של מוט דק באורך , מומנט האינרציה שלו ביחס למרכז המסה הוא . נציב:

הראנו ש- , ולכן:

נחשב את האנרגיה הפוטנציאלית:

נציב כעת בשימור אנרגיה, כאשר נשווה למצב ההתחלתי:

זוהי משוואה פרידה שניתן ממנה לחלץ ביטוי מפורש ל-.

תרגילים

שאלה 1

מכונית צעצוע בנויה מעגלה בעלת ארבעה גלגלים שעליה מורכב גלגל תנופה הסובב סביב ציר אופקי כמתואר. רדיוס גלגל התנופה הוא , רוחבו זניח ומרכזו נמצא בגובה מעל לקרקע. מסת גלגל התנופה היא , ומסת שאר רכיבי המערכת זניחה. המכונית נעה על משטח אופקי במסלול מעגלי שרדיוסו (). לגאומטרייה של המכונית יש סימטריה אורכית ורוחבית (סימטריה ימין-שמאל, וקדימה- אחורה).

book

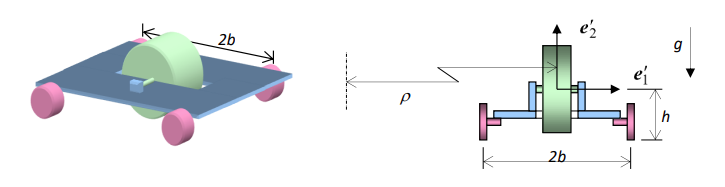
סכימת המכונית צעצוע

היות ומרכז המסה של המכונית נמצא בגובה מעל למשטח, קיימת אפשרות שאם המכונית תנוע מהר מידי היא תתהפך הצידה. המכונית נעה קדימה בכיוון במהירות קבועה , וקצב סיבוב גלגל התנופה ביחס למכונית הוא .

פתרון:
book

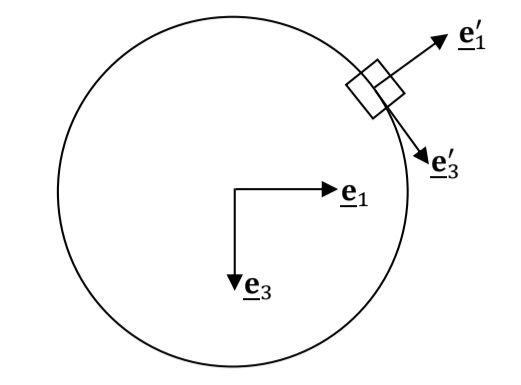
מבט צד על מסלול המכונית

דרוש:

סעיף א’

כאשר , מהי המהירות בה תתהפך המכונית?

פתרון:
לפי הגדרת מערכת הצירים , ועצם העובדה שהמהירות המשיקית של המכונית קבועה וגודלה , המהירות הזוויתית של מערכת צירים זו היא:

מאזן תנע קווי על הגק”ש:
נבצע מאזן תנע קווי:
book

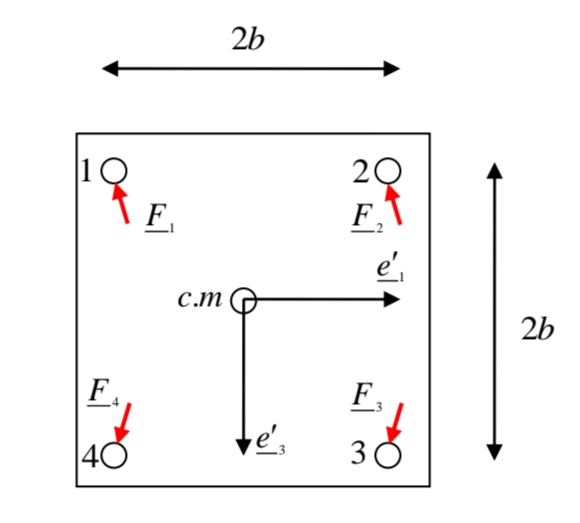
דג”ח ממבט על

סכום הכוחות עבור כל אחד מהגלגלים :

כאשר הוא כוח הריאקציה, הוא הכוח הנורמלי, ו- הוא כוח החיכוך.
מסימטריה, הכוחות על הגלגלים הפנימיים זהים, והכוחות על הגלגלים החיצוניים זהים, ונסמנם:

מאחר והמכונית בתנועה מעגלית קצובה (מהירות משיקית קבועה), תאוצת מרכז המסה שלה היא פשוט:

נציב הכל במאזן תנע קווי:

קיבלנו שלושה משוואות:

מאזן תנע זוויתי על הגק”ש:
מתנע זוויתי יחסית למרכז המסה:

הסיבוב של הגק”ש נתון כ:

טנזור האינרציה של גלגל:

ולכן התנע הזוויתי:

נגזור לפי כלל האופרטור (כאשר נניח כי ):

ולכן:

נחשב את המומנטים סביב מרכז המסה:

נשווה לפי מאזן תנע זוויתי ונקבל שלושה משוואות:

ממשוואות (1) ו-(2) נקבל:

כעת עבור כל אחד מהסעיפים, נציב את הנתונים הרלוונטיים.
בסעיף הנוכחי, מתקיים . המכונית תתחיל להתהפך ברגע בו . נציב:

סעיף ב’

כאשר ו- , מהו גודל הריאקציה האנכית על כל אחד מהגלגלים הפנימיים לסיבוב?

פתרון:
נציב פשוט :

סעיף ג’

כאשר וגלגל התנופה סובב באותו כיוון כמו גלגלי העגלה ובקצב , מה גודל הריאקציה האנכית על כל אחד מהגלגלים החיצוניים לסיבוב?

פתרון:
נציב את הנתונים ונקבל:

סעיף ד’

כאשר מהו קצב הסיבוב של גלגל התנופה אשר יבטל לחלוטין את מומנט ההתהפכות (הריאקציה האנכית בכל הגלגלים זהה)?

פתרון:
נדרוש ש- , ונקבל:

עמודים המציינים את העמוד הזה