ELM1_006 שנאים

→ קודם: ELM1_005הבא: ELM1_007 ←

מבוא

אם נסדר שני סלילים מבודדים חשמלית זה מזה כך שהשטף המשתנה בזמן הנוצר על ידי אחד מהם גורם לכוח אלקטרו-מניע (כא”מ) להיות מושרה בשני, נאמר שהם יוצרים שנאי (transformer). במילים אחרות, שנאי הוא התקן הכולל סלילים המצומדים מגנטית. אם רק חלק מהשטף הנוצר על ידי סליל אחד מקושר לשני, נאמר שהסלילים מצומדים באופן רופף (loosely coupled). במקרה זה, פעולת השנאי אינה יעילה במיוחד. על מנת להגדיל את הצימוד בין הסלילים, הם מלופפים על ליבה (core) משותפת. כאשר הליבה עשויה מחומר לא מגנטי, השנאי נקרא שנאי ליבת אוויר (air-core transformer). כאשר הליבה עשויה מחומר פרומגנטי בעל פרמביליות גבוהה יחסית, השנאי מכונה שנאי ליבת ברזל (iron-core transformer). ליבה מגנטית בעלת פרמביליות גבוהה מבטיחה כי-

1. כמעט כל השטף הנוצר על ידי סליל אחד מצומד לשני ו-
2. הרילקטנס של הנתיב המגנטי נמוך. התוצאה היא פעולה יעילה ביותר של השנאי.

תדירות הכא”מ המושרה בסליל השני זהה לזו של הזרם בסליל הראשון. אם הסליל השני מחובר לעומס, הכא”מ המושרה בסליל יוצר בו זרם. כך, ההספק מועבר מסליל אחד לשני דרך השטף המגנטי בליבה. הסליל שאליו המקור מספק את ההספק נקרא הליפוף הראשי (primary winding). הסליל המספק הספק לעומס נקרא הליפוף המשני (secondary winding). כל אחד מהליפופים יכול להיות מחובר למקור ו/או לעומס.

מאחר שהכא”מ המושרה בסליל פרופורציונלי למספר הכריכות בסליל, ניתן לקבל מתח גבוה יותר על פני הליפוף המשני מאשר המתח המופעל על הליפוף הראשי. במקרה זה, השנאי נקרא שנאי מעלה מתח (step-up transformer). שנאי מעלה מתח משמש לחיבור קו תמסורת במתח גבוה יחסית לגנרטור במתח נמוך יחסית. מצד שני, שנאי מוריד מתח (step-down transformer) הוא בעל מתח נמוך יותר בצד המשני. דוגמה לשנאי מוריד מתח היא שנאי ריתוך, שהמשני שלו מתוכנן לספק זרם עומס גבוה.

כאשר המתח המופעל על הראשי שווה לכא”מ המושרה במשני, נאמר שלשנאי יש יחס השנאה של אחד לאחד (one-to-one ratio). שנאי בעל יחס השנאה של אחד לאחד משמש בעיקר לצורך בידוד חשמלי של הצד המשני מהצד הראשי שלו. שנאי כזה נקרא בדרך כלל שנאי בידוד (isolation transformer). שנאי בידוד יכול לשמש לבידוד זרם ישר (DC). כלומר, אם מתח הכניסה בצד הראשי מורכב הן מרכיבי DC והן מרכיבי זרם חילופין (AC), המתח בצד המשני יהיה AC טהור.

מבנה השנאי

על מנת לשמור על הפסדי ליבה מינימליים, ליבת השנאי בנויה מלמינציות דקות של חומר פרומגנטי בעל פרמביליות גבוהה, כגון פלדת סיליקון. פלדת סיליקון משמשת בשל תכונותיה שאינן מתיישנות והפסדיה המגנטיים הנמוכים. עובי הלמינציה נע בין ל- . ציפוי דק של לכה נמרח על שני צידי הלמינציה על מנת לספק התנגדות גבוהה בין הלמינציות. תהליך חיתוך הלמינציות לגודל המתאים גורם למאמצי ניקוב וגזירה. מאמצים אלו גורמים לעלייה בהפסדי הליבה. על מנת להסיר את מאמצי הניקוב והגזירה, הלמינציות עוברות חימום בטמפרטורות גבוהות בסביבה מבוקרת למשך זמן מה. תהליך זה ידוע בשם תהליך חישול (annealing process).

קיימים שני סוגי מבנה עיקריים בשימוש נפוץ עבור שנאים: מבנה מעטפת (shell type) ומבנה ליבה (core type). במבנה של שנאי מסוג מעטפת, שני הליפופים מלופפים בדרך כלל על אותה רגל של הליבה המגנטית, כפי שמוצג באיור הבא:

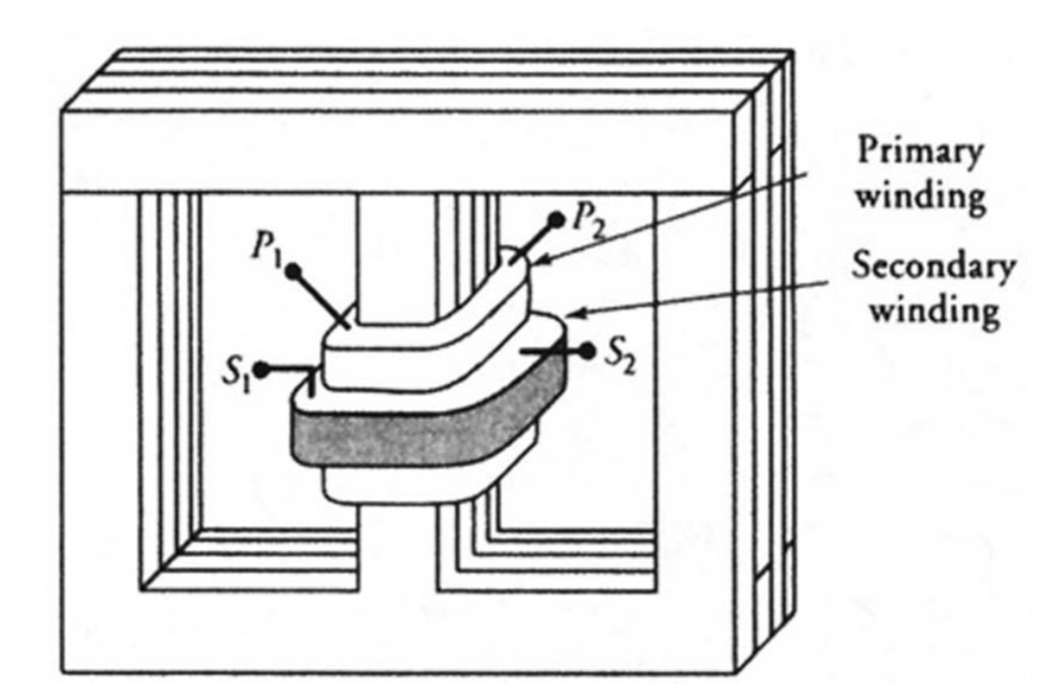
שנאי מסוג מעטפת. (Guru, 2001).

בשנאי מסוג ליבה, המוצג באיור הבא, כל ליפוף עשוי להיות מחולק באופן שווה ומלופף על שתי רגלי הליבה המלבנית. המינוח, סוג מעטפת וסוג ליבה, נובע מהעובדה שבשנאי מסוג מעטפת הליבה מקיפה את הליפופים, בעוד שבשנאי מסוג ליבה הליפופים עוטפים את הליבה.

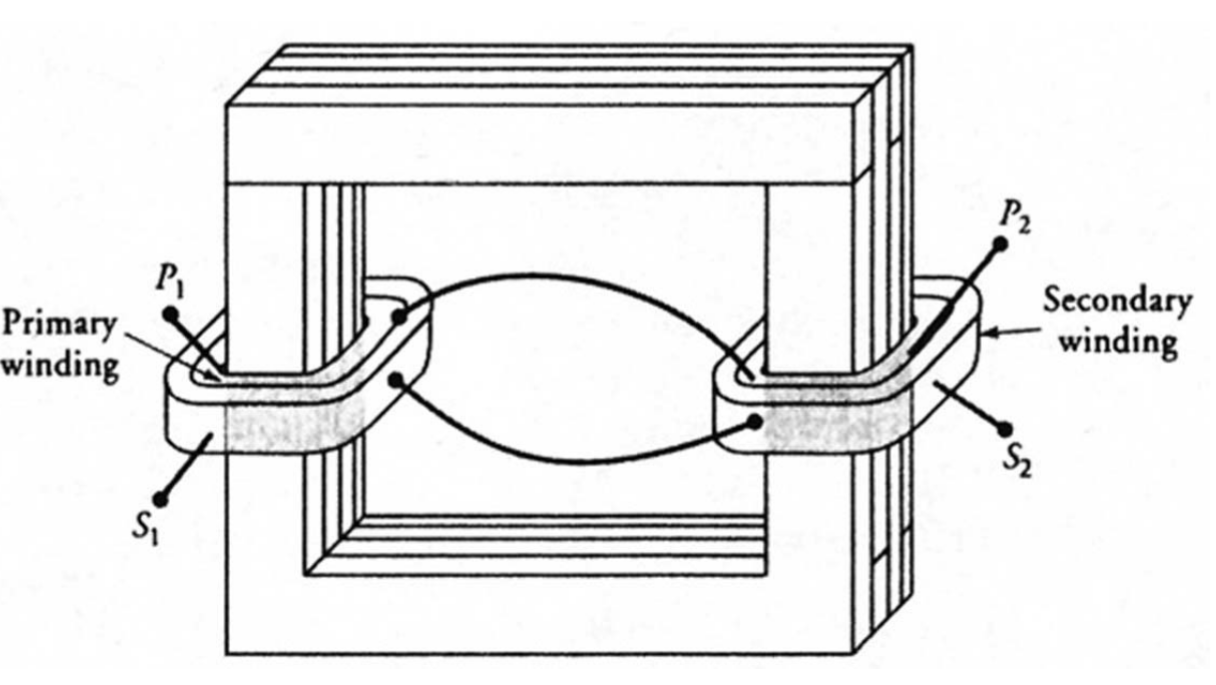
שנאי מסוג ליבה. (Guru, 2001).

עבור יישומי הספק נמוכים יחסית עם דירוגי מתח מתונים, ניתן ללפף את הליפופים ישירות על ליבת השנאי. עם זאת, עבור שנאים במתח גבוה ו/או בהספק גבוה, הסלילים לרוב מלופפים מראש (form-wound) ולאחר מכן מורכבים על הליבה.

הן הפסדי הליבה (הפסדי היסטרזיס וזרמי מערבולת) והן הפסדי הנחושת (הפסדים חשמליים) בשנאי מייצרים חום, אשר בתורו מעלה את טמפרטורת הפעולה של השנאי. עבור יישומי הספק נמוך, זרימת אוויר טבעית עשויה להספיק כדי לשמור על טמפרטורת השנאי בטווח קביל. אם לא ניתן לשלוט בעליית הטמפרטורה באמצעות זרימת אוויר טבעית, ניתן לקרר שנאי על ידי הזרמת אוויר רציפה דרך הליבה והליפופים שלו. כאשר זרימת אוויר מאולצת אינה מספיקה, ניתן לטבול שנאי בשמן שנאים, המוביל את החום לדפנות מיכל האחסון. על מנת להגדיל את שטח הפנים הקורן של המיכל, ניתן לרתך צלעות קירור למיכל או לבנות את המיכל מלוחות פלדה גליים.

שנאי אידיאלי

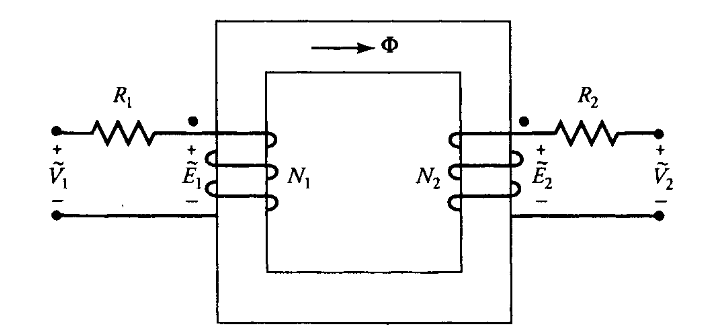
שנאי בעל שני ליפופים, כאשר כל ליפוף פועל כחלק ממעגל חשמלי נפרד, מוצג באיור הבא:

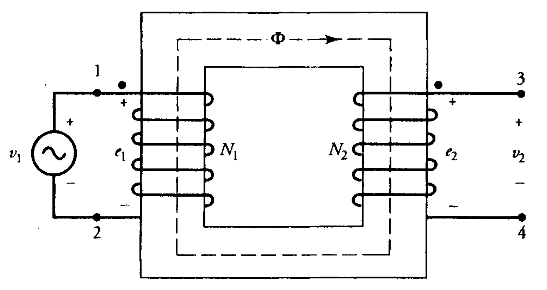
שנאי אידיאלי תחת אפס עומס. (Guru, 2001).

יהיו ו- מספרי הכריכות בליפוף הראשי והמשני, בהתאמה. הליפוף הראשי מחובר למקור מתח משתנה בזמן , בעוד שהליפוף המשני נותר פתוח. לשם ההבנה, נתייחס תחילה לשנאי אידיאלי שבו אין הפסדים ואין שטף זליגה. במילים אחרות, אנו מניחים את ההנחות הבאות:

1. ליבת השנאי בעלת פרמביליות גבוהה מאוד, במובן שהיא דורשת כוח מגנטו-מניע (כמ”מ) זניח כדי ליצור את השטף כפי שמוצג באיור.
2. הליבה אינה חווה הפסדי זרמי מערבולת או היסטרזיס.
3. כל השטף מוגבל לזרום בתוך הליבה.
4. ההתנגדות של כל ליפוף זניחה.

על פי חוק פאראדיי, השטף המגנטי בליבה משרה כא”מ בליפוף הראשי, המתנגד למתח המופעל . עבור הקוטביות של המתח המופעל והכא”מ המושרה, כפי שמצוין באיור עבור הליפוף הראשי, נוכל לכתוב:

באופן דומה, הכא”מ המושרה בליפוף המשני הוא:

עם קוטביות כפי שמצוין באיור. במקרה האידיאלי המונח, הכא”מ המושרה ו- שווים למתחי ההדקים המתאימים ו-, בהתאמה. לפיכך, ממשוואות (GU4.1) ו-(GU4.2), אנו מקבלים:

משוואה זו קובעת כי היחס בין הכא”מ המושרה הראשי למשני שווה ליחס בין מספר הכריכות הראשי למשני. מקובל להגדיר את היחס בין מספר הכריכות הראשי למשני כיחס ההשנאה :

יהי הזרם דרך הליפוף המשני כאשר הוא מחובר לעומס, כפי שמוצג באיור הבא:

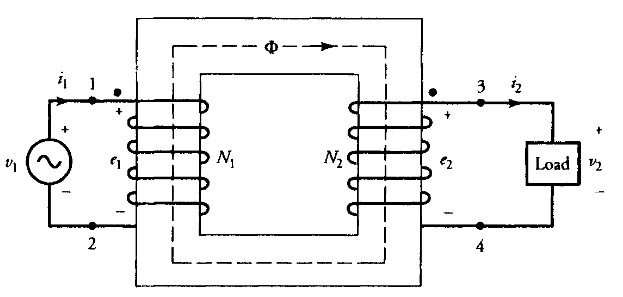
שנאי אידיאלי תחת עומס. (Guru, 2001).

גודל תלוי באימפידנס העומס. עם זאת, כיוונו הוא כזה שהוא נוטה להחליש את שטף הליבה ולהקטין את הכא”מ המושרה בראשי . עבור שנאי אידיאלי, חייב תמיד להיות שווה ל-. במילים אחרות, השטף בליבה חייב תמיד להיות שווה לערכו המקורי ללא עומס. על מנת להחזיר את השטף בליבה לערכו המקורי ללא עומס, המקור מאלץ זרם לזרום בליפוף הראשי, כפי שמצוין באיור. בהתאם להנחותינו, הכמ”מ של הזרם הראשי חייב להיות שווה והפוך לכמ”מ של המשני . כלומר,

או

משוואה זו קובעת שהזרמים הראשי והמשני עוברים השנאה ביחס הפוך למספר הכריכות.

ממשוואות (GU4.3) ו-(GU4.5), ברור כי:

משוואה זו מאשרת בפשטות את הנחתנו בדבר היעדר הפסדים בשנאי אידיאלי. היא מדגישה את העובדה שבכל רגע נתון, ההספק המוצא (הנמסר לעומס) שווה להספק הנכנס (המסופק על ידי המקור).

עבור שינויים סינוסואידיים במתח המופעל, השטף המגנטי בליבה משתנה גם הוא באופן סינוסואידי בתנאים אידיאליים. אם השטף בליבה בכל רגע נתון על ידי:

כאשר היא אמפליטודת השטף ו- היא התדירות הזוויתית, אז הכא”מ המושרה בראשי הוא:

ניתן לבטא את המשוואה לעיל בצורה פאזורית במונחים של ערכה האפקטיבי (RMS):

באופן דומה, הכא”מ המושרה בליפוף המשני הוא:

ממשוואות (GU4.7) ו-(GU4.8), אנו מקבלים:

כאשר וגם בתנאים אידיאליים. מהמשוואה לעיל, ברור שהכא”מ המושרה נמצאים במופע. עבור שנאי אידיאלי, גם מתחי ההדקים נמצאים במופע.

מדרישות הכמ”מ, נוכל גם להסיק כי:

כאשר ו- הם הזרמים בצורה פאזורית דרך הליפופים הראשי והמשני. משוואה זו מחייבת ש- ו- יהיו במופע עבור שנאי אידיאלי.

ניתן לבטא את משוואה (GU4.6) גם במונחים של גדלים פאזוריים כ:

כלומר, ההספק המרוכב המסופק לליפוף הראשי על ידי המקור שווה להספק המרוכב הנמסר לעומס על ידי הליפוף המשני. במונחים של הספקים נדמים, המשוואה לעיל הופכת ל:

אם הוא אימפידנס העומס בצד המשני, אז:

או

כאשר הוא אימפידנס העומס כפי שהוא נראה מהצד הראשי. משוואה (GU4.13) קובעת שאימפידנס העומס כפי שהוא נראה על ידי המקור בצד הראשי שווה לפי מאימפידנס העומס האמיתי בצד המשני. משוואה זו קובעת שניתן להשתמש בשנאי גם לתיאום אימפידנסים (impedance matching). ניתן להעלות או להוריד אימפידנס ידוע כדי להתאימו לשאר המעגל לצורך העברת הספק מרבית.

קוטביות שנאי

לשנאי עשויים להיות מספר ליפופים שעשויים להיות מחוברים בטור להגדלת דירוג המתח או במקביל להגדלת דירוג הזרם. לפני ביצוע החיבורים, עם זאת, הכרחי שנדע את הקוטביות של כל ליפוף. בקוטביות אנו מתכוונים לכיוון היחסי של הכא”מ המושרה בכל ליפוף. נבחן את השנאי המוצג באיור לעיל. תהי קוטביות מקור המתח המשתנה בזמן המחובר לליפוף הראשי, בכל רגע נתון, כפי שמצוין באיור. מאחר שהכא”מ המושרה בראשי של שנאי אידיאלי חייב להיות שווה והפוך למתח המופעל , הדק 1 של הראשי חיובי ביחס להדק 2. כיוון הליפוף של הליפוף הראשי כפי שמוצג באיור אחראי לכיוון השטף עם כיוון השעון בליבת השנאי. שטף זה חייב להשרות בליפוף המשני כא”מ הגורם לזרם כפי שמצוין. כיוון הזרם הוא כזה שהוא יוצר שטף המתנגד לשינוי בשטף המקורי . עבור כיוון הליפוף של הליפוף המשני כפי שמתואר באיור, הדק 3 חייב להיות חיובי ביחס להדק 4. מאחר שלהדק 3 יש אותה קוטביות כמו להדק 1, נאמר שהם עוקבים זה אחר זה. במילים אחרות, הדקים 1 ו-3 הם הדקים בעלי קוטביות זהה. כדי לציין את יחס הקוטביות הזהה, שרטטנו נקודות בהדקים אלו.

דירוגי שנאי

לוחית השם של שנאי מספקת מידע על ההספק הנדמה וקיבולת המתח של כל ליפוף. מנתוני לוחית השם של שנאי מוריד מתח , , אנו מסיקים את הדברים הבאים:

1. דירוג ההספק המלא או הנומינלי של השנאי הוא . במילים אחרות, השנאי יכול לספק באופן רציף.
2. מאחר שמדובר בשנאי מוריד מתח, המתח הראשי (הנומינלי) הוא והמתח המשני (הנומינלי) הוא .
3. הגדלים הנומינליים של הזרמים הראשי והמשני בעומס מלא הם:
   $$
   I_1 = \frac{5000}{500} = \pu{10 A} וכן
4. מאחר שהמידע על מספר הכריכות אינו נמסר בדרך כלל על ידי היצרן, אנו קובעים את יחס ההשנאה מהמתחים הנומינליים בהדקים:
   $$
   a = \frac{V_1}{V_2} = \frac{500}{250} = 2

שנאי לא אידיאלי

בסעיף הקודם הצבנו מספר מגבלות כדי לקבל יחסים שימושיים עבור שנאי אידיאלי. בסעיף זה, מטרתנו היא להסיר מגבלות אלו על מנת לפתח מעגל שקול עבור שנאי לא אידיאלי.

התנגדויות הליפופים

אף על פי שהיא קטנה, לכל ליפוף יש התנגדות מסוימת. אף על פי כן, אנו יכולים להחליף שנאי לא אידיאלי בשנאי אידיאלי על ידי הכללת (להכיל) התנגדות מקובצת השווה להתנגדות הליפוף בטור עם כל ליפוף. כפי שמוצג באיור הבא, ו- הן התנגדויות הליפופים של הראשי והמשני, בהתאמה. הכללת התנגדויות הליפופים מחייבת כי

1. הספק המבוא חייב להיות גדול מהספק המוצא, ו-
2. מתח ההדקים אינו שווה לכא”מ המושרה, וכן-
3. נצילות (היחס בין הספק המוצא להספק המבוא) של שנאי לא אידיאלי קטנה מ-.

שנאי אידיאלי עם התנגדויות ליפופים הממודלות כהתנגדויות מקובצות. (Guru, 2001).

שטפי זליגה

לא כל השטף הנוצר על ידי ליפוף נשאר בתוך הליבה המגנטית שעליה הליפוף מלופף. חלק מהשטף, המכונה שטף זליגה (leakage flux), משלים את מסלולו דרך האוויר. לכן, כאשר שני הליפופים בשנאי נושאים זרמים, כל אחד יוצר שטף זליגה משלו, כפי שמודגם באיור הבא. שטף הזליגה הראשי שנוצר על ידי הראשי אינו מקושר למשני. באופן דומה, שטף הזליגה המשני מגביל את עצמו למשני ואינו מקושר לראשי. השטף המשותף הזורם בליבה ומקשר את שני הליפופים מכונה שטף הדדי (mutual flux).

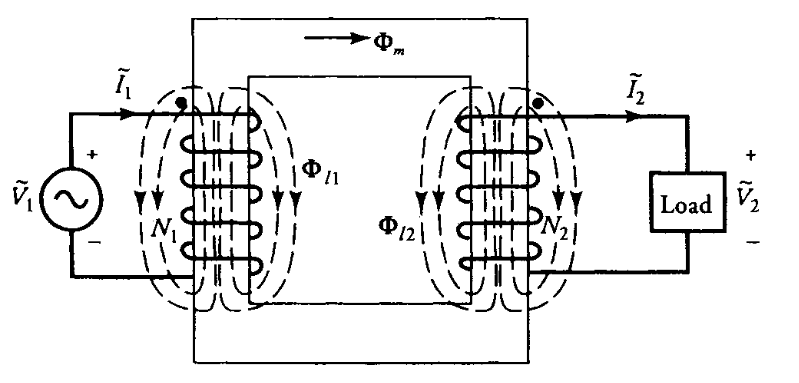
שנאי עם שטפי זליגה ושטף הדדי. (Guru, 2001).

אף על פי ששטף זליגה הוא חלק קטן מהשטף הכולל הנוצר על ידי ליפוף, הוא אכן משפיע על ביצועי השנאי. אנו יכולים למדל ליפוף כאילו הוא מורכב משני ליפופים: ליפוף אחד אחראי ליצירת שטף הזליגה דרך האוויר, והשני מקיף את הליבה. סידורי ליפופים היפותטיים כאלה מוצגים באיור הבא עבור שנאי דו-ליפופי:

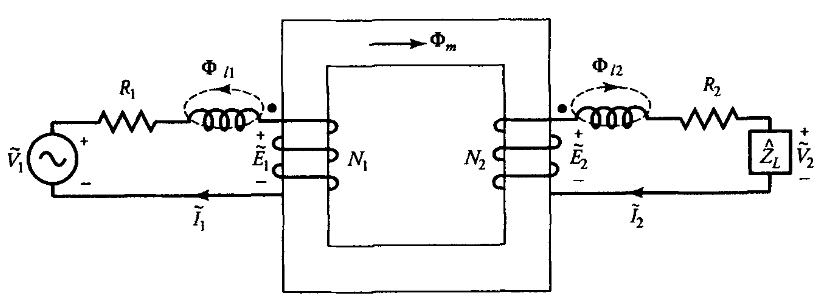
ליפופים היפותטיים המציגים בנפרד קישורי שטף זליגה ושטף הדדי. (Guru, 2001).

שני הליפופים העוטפים את הליבה מקיימים כעת את התנאים של שנאי אידיאלי. שטף הזליגה המשויך לכל ליפוף אחראי למפל המתח עליו. לכן, אנו יכולים לייצג את מפל המתח עקב שטף הזליגה על ידי ריאקטנס זליגה. אם ו- הם ריאקטנסי הזליגה של הליפופים הראשי והמשני, ניתן לייצג שנאי אמיתי במונחים של שנאי אידיאלי עם התנגדויות ליפופים וריאקטנסי זליגה כפי שמוצג באיור הבא:

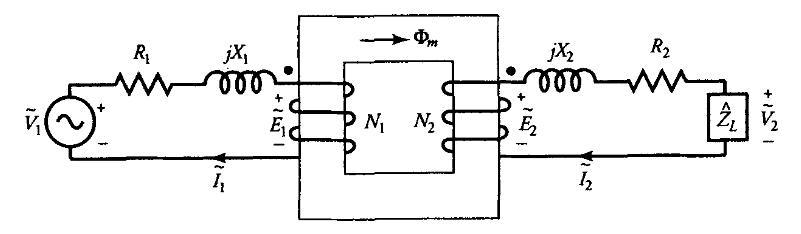
שנאי לא אידיאלי המיוצג במונחים של שנאי אידיאלי עם התנגדויות ליפופים וריאקטנסי זליגה. (Guru, 2001).

במקרה של שנאי לא אידיאלי:

יש לשים לב שבשנאי לא אידיאלי, ו- .

דוגמה:

שנאי מוריד מתח , , בעל ערכי ההתנגדות והריאקטנס זליגה הבאים: , , , ו-. השנאי פועל ב- מהעומס הנקוב שלו. אם מקדם ההספק של העומס הוא , קבעו את נצילות השנאי.

פתרון:
מאחר שהשנאי פועל ב- מהעומס הנקוב שלו, הערך האפקטיבי של זרם הליפוף המשני הוא:

בהנחה שמתח העומס הוא הייחוס, זרם העומס במקדם הספק מקדים של , בצורה פאזורית, הוא (זווית של ):

אימפדנס הליפוף המשני הוא:

הכא”מ המושרה בליפוף המשני הוא:

מאחר שיחס ההשנאה הוא:

נוכל לקבוע את הכא”מ המושרה והזרם בצד הראשי:

אימפדנס הליפוף הראשי הוא:

לכן, מתח המקור חייב להיות:

ההספק המסופק לעומס הוא:

הספק הכניסה הוא:

לכן נצילות השנאי היא:

פרמביליות סופית ואובדני ליבה

לליבה של שנאי לא אידיאלי יש פרמביליות סופית ואובדני ליבה. לכן, גם כאשר המשני נותר פתוח (מצב ללא עומס), הליפוף הראשי צורך זרם מסוים מהמקור, המכונה זרם עירור (excitation current). מקובל להניח שזרם העירור, , הוא סכום של שני זרמים: זרם אובדני הליבה, , וזרם המגנוט, . כלומר,

רכיב אובדני הליבה של זרם העירור אחראי להפסדים המגנטיים (הפסדי היסטרזיס והפסדי זרמי מערבולת) בליבת השנאי. אם הוא הכא”מ המושרה בצד הראשי ו- היא התנגדות אובדני הליבה השקולה, אז זרם אובדני הליבה, , הוא:

רכיב המגנוט של זרם העירור אחראי ליצירת השטף ההדדי בליבה. מאחר שסליל נושא זרם מהווה משרן, זרם המגנוט, , יוצר ריאקטנס מגנוט, . לפיכך,

כעת אנו יכולים לשנות את המעגל השקול של האיור הקודם כך שיכלול את התנגדות אובדני הליבה וריאקטנס המגנוט. מעגל כזה מוצג באיור הבא:

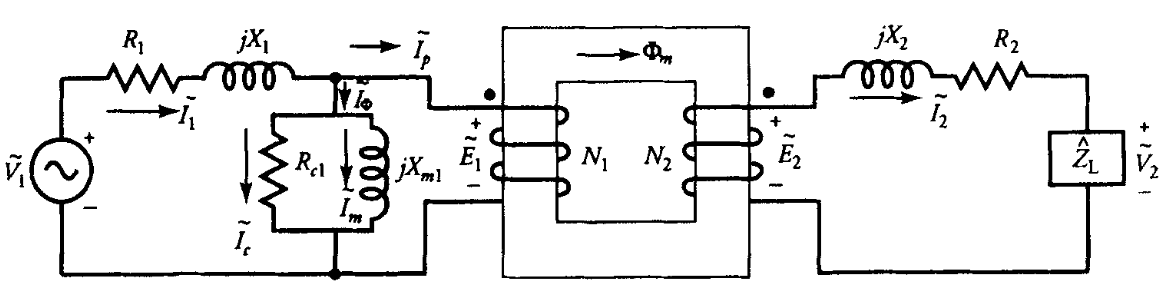
מעגל שקול של שנאי הכולל התנגדויות ליפופים, ריאקטנס זליגה, התנגדות אובדני ליבה, ריאקטנס מגנוט ושנאי אידיאלי. (Guru, 2001).

כאשר אנו מגדילים את העומס על השנאי, מתרחש רצף האירועים הבא:

1. זרם הליפוף המשני גדל.
2. הזרם המסופק על ידי המקור גדל.
3. מפל המתח על פני אימפדנס הליפוף הראשי גדל.
4. הכא”מ המושרה יורד.
5. לבסוף, השטף ההדדי קטן עקב הירידה בזרם המגנוט.

עם זאת, בשנאי מתוכנן היטב, הירידה בשטף ההדדי ממצב ללא עומס למצב עומס מלא היא בערך עד . לכן, לכל המטרות המעשיות, אנו יכולים להניח ש- נשאר זהה. במילים אחרות, השטף ההדדי זהה במהותו בתנאי עומס רגילים, ולכן אין שינוי ניכר בזרם העירור. בייצוג המעגל השקול של שנאי, הליבה מוצגת לעתים רחוקות. לפעמים, קווים מקבילים נמשכים בין שני הליפופים כדי לציין את נוכחותה של ליבה מגנטית. אנו נשתמש בייצוג מעגל שקול כזה. אם הקווים המקבילים בין שני הליפופים חסרים, הפרשנות שלנו היא שהליבה אינה מגנטית. מתוך הבנה זו, המעגל השקול המדויק של שנאי אמיתי ניתן באיור הבא:

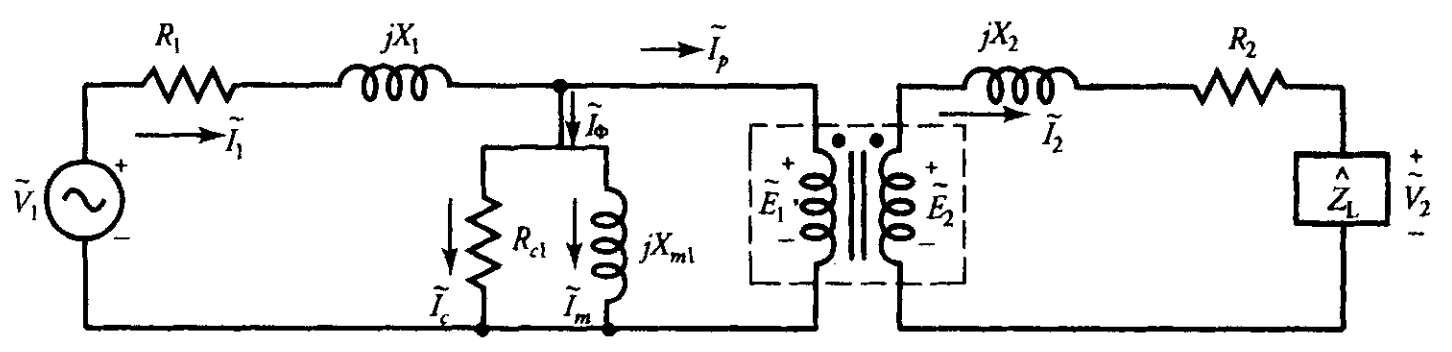
מעגל שקול מדויק של שנאי אמיתי. הסלילים המצומדים בתיבה המקווקוות מייצגים שנאי אידיאלי עם ליבה מגנטית. (Guru, 2001).

באיור זה, מצוירת גם תיבה מקווקוות כדי להראות שהמעגל התחום בה הוא מה שמכונה שנאי אידיאלי. ניתן ליישם את כל יחסי השנאי האידיאלי על מעגל זה.

זרם העומס בצד המשני מיוצג בצד הראשי כ- . כעת ניתן לקבוע את זרם העירור כ:

ניתן לייצג שנאי על ידי מעגל שקול שאינו משתמש בשנאי אידיאלי. מעגלים שקולים כאלה מצוירים בהתייחסות לליפוף נתון. האיור הבא מציג מעגל שקול כזה כפי שהוא נראה מהצד הראשי. שימו לב שרכיבי המעגל שהיו בצד המשני באיור לעיל הועברו לצד הראשי:

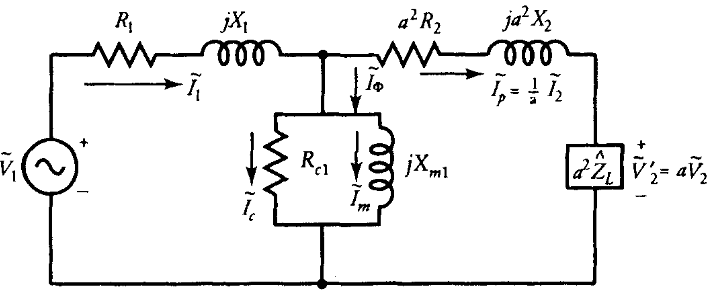
המעגל השקול המדויק כפי שנראה מהצד הראשי של השנאי. (Guru, 2001).

האיור הבא מציג את המעגל השקול של אותו שנאי כפי שהוא מיוחס לצד המשני.

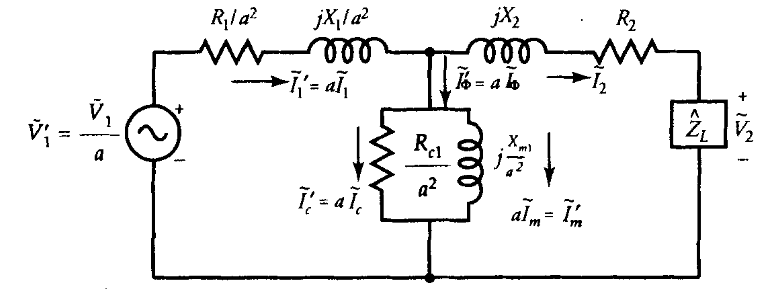
מעגל שקול מדויק כפי שנראה מהצד המשני של השנאי. (Guru, 2001).

קירוב למעגלים שקולים

בשנאי מתוכנן היטב, התנגדויות הליפופים, ריאקטנסי הזליגה ואובדני הליבה נשמרים נמוכים ככל האפשר. אובדני ליבה נמוכים מרמזים על התנגדות אובדני ליבה גבוהה. הפרמביליות הגבוהה של הליבה מבטיחה ריאקטנס מגנוט גבוה. לפיכך, האימפדנס של מה שמכונה הענף המקבילי ( במקביל ל-) על פני הראשי גבוה מאוד בהשוואה ל- ו-. האימפדנס הגבוה של הענף המקבילי מבטיח זרם עירור נמוך. בניתוח של מערכות הספק מורכבות, ניתן להשיג פישוט רב על ידי הזנחת זרם העירור. מאחר ש- נשמר נמוך, מפל המתח עליו נמוך גם הוא בהשוואה למתח המופעל. מבלי להכניס שגיאה ניכרת בחישובינו, אנו יכולים להניח שמפל המתח על פני הענף המקבילי זהה למתח המופעל. הנחה זו מאפשרת לנו להזיז את הענף המקבילי כפי שמצוין באיור הבא עבור המעגל השקול של שנאי המגלם שנאי אידיאלי. זה מכונה המעגל השקול המקורב של שנאי.

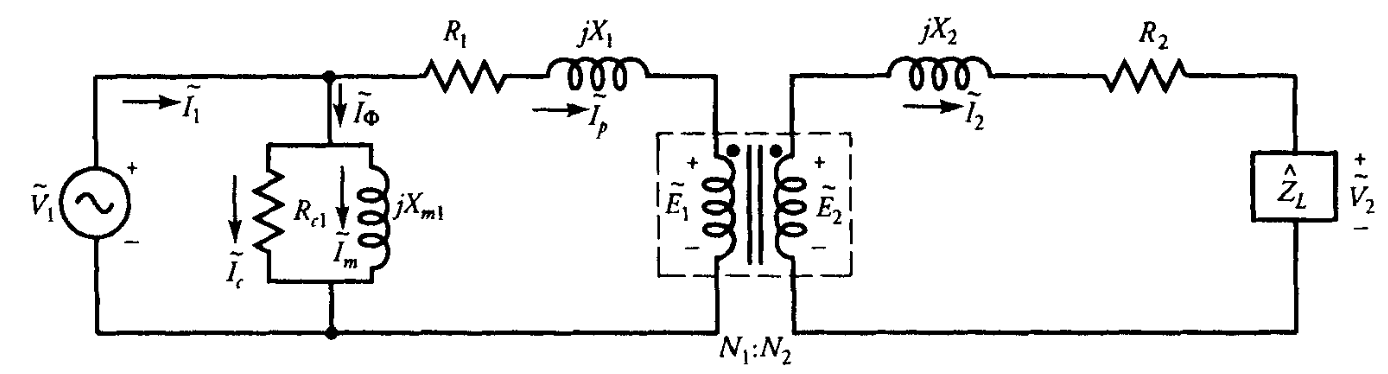
מעגל שקול מקורב של שנאי. (Guru, 2001).

המעגל השקול המקורב כפי שנראה מהצד הראשי ניתן באיור הבא, כאשר:

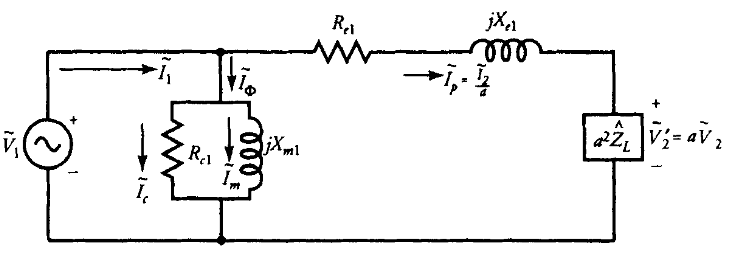
מעגל שקול מקורב של שנאי כפי שנראה מהצד הראשי. (Guru, 2001).

באופן דומה, האיור הבא מציג את המעגל השקול המקורב כפי שהוא מיוחס לצד המשני של השנאי. באיור זה:

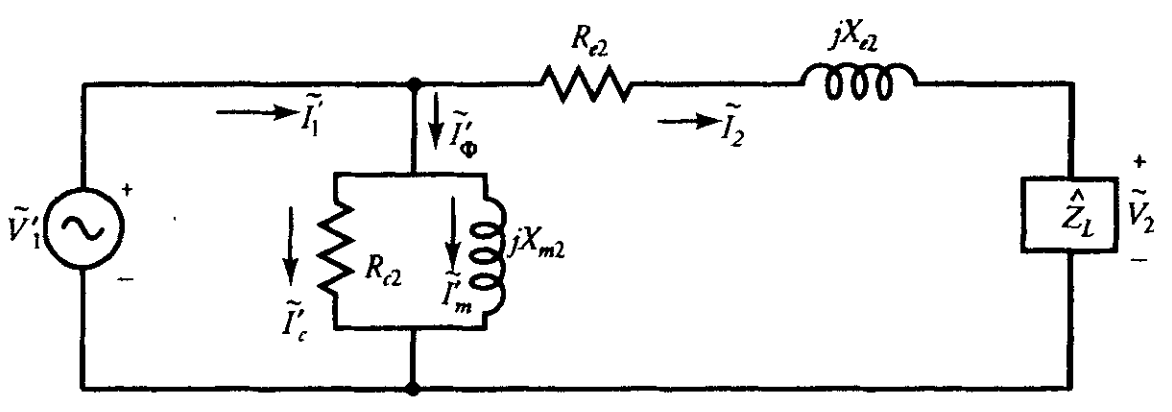
מעגל שקול מקורב של שנאי כפי שנראה מהצד המשני. (Guru, 2001).

קביעת פרמטרי שנאי

ניתן לקבוע את פרמטרי המעגל השקול של שנאי על ידי ביצוע שני ניסויים: ניסוי מעגל פתוח (open-circuit test) וניסוי קצר (short-circuit test).

ניסוי מעגל פתוח

כפי שמשתמע מהשם, ליפוף אחד של השנאי נותר פתוח בעוד שהשני מעורר על ידי הפעלת המתח הנקוב. תדירות המתח המופעל חייבת להיות התדירות הנקובה של השנאי. למרות שאין זה משנה איזה צד של השנאי מעורר, בטוח יותר לבצע את הניסוי בצד המתח הנמוך. הצדקה נוספת לביצוע הניסוי בצד המתח הנמוך היא הזמינות של מקור מתח נמוך בכל מתקן בדיקה. האיור הבא מציג את תרשים החיבורים לניסוי מעגל פתוח עם מד זרם, מד מתח ומד הספק המחוברים בצד המתח הנמוך.

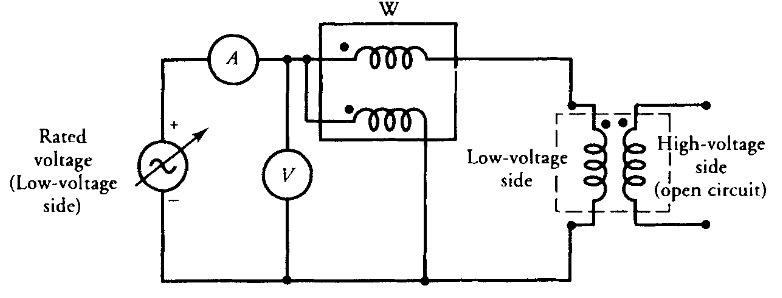
שנאי דו-ליפופי מחובר עם מכשירים לניסוי מעגל פתוח. (Guru, 2001).

אם נניח שהפסד ההספק במצב ללא עומס בליפוף המתח הנמוך זניח, אז המעגל השקול המקורב המתאים כפי שנראה מצד המתח הנמוך ניתן באיור הבא:

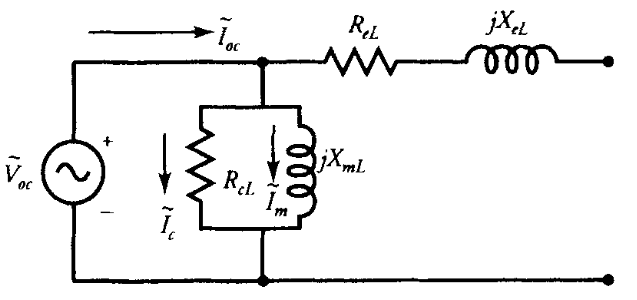
המעגל השקול המקורב של שנאי דו-ליפופי בניסוי מעגל פתוח. (Guru, 2001).

מהמעגל השקול המקורב של השנאי כפי שהוא מיוחס לצד המתח הנמוך (האיור לעיל), ניכר כי המקור מספק ( עבור open-circuit) את זרם העירור במצב ללא עומס. רכיב אחד של זרם העירור אחראי להפסדי הליבה, בעוד שהשני אחראי ליצירת השטף הנדרש בליבה המגנטית. על מנת למדוד ערכים אלו במדויק, יש לכוונן בזהירות את מתח המקור לערכו הנקוב. מאחר שהפסד ההספק היחיד באיור לעיל הוא הפסד הליבה, מד ההספק מודד את הפסד הליבה בשנאי.

רכיב הפסדי הליבה של זרם העירור נמצא במופע עם המתח המופעל בעוד שזרם המגנוט מפגר אחרי המתח המופעל ב-, כפי שמוצג באיור הבא:

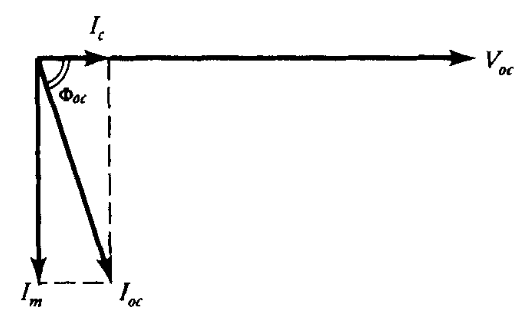
דיאגרמת הפאזורים של שנאי דו-ליפופי בניסוי מעגל פתוח. (Guru, 2001).

אם הוא המתח הנקוב המופעל בצד המתח הנמוך, הוא זרם העירור כפי שנמדד על ידי מד הזרם, ו- הוא ההספק הנרשם על ידי מד ההספק, אז ההספק הנדמה במצב ללא עומס הוא

בזווית מקדם הספק מפגרת של

זרמי הפסדי הליבה והמגנוט הם:

וכן

לפיכך, התנגדות הפסדי הליבה ( עבור core ו- עבור low) והריאקטנס המגנטי ( עבור magnetizing) כפי שהם נראים מצד המתח הנמוך הם:

וכן

כאשר

ניסוי קצר

ניסוי זה נועד לקבוע את התנגדויות הליפופים וריאקטנסי הזליגה. ניסוי הקצר מבוצע על ידי הצבת קצר על פני ליפוף אחד ועירור הליפוף השני ממקור מתח חילופין בתדירות שבה השנאי מדורג. המתח המופעל מכוונן בזהירות כך שכל ליפוף נושא זרם נקוב. הזרם הנקוב בכל ליפוף מבטיח הדמיה נכונה של תבנית שטף הזליגה המשויכת לליפוף זה. מאחר שהקצר מגביל את הספק המוצא לאפס, הספק הכניסה לשנאי נמוך. הספק הכניסה הנמוך בזרם הנקוב מרמז שהמתח המופעל הוא שבריר קטן מהמתח הנקוב. לכן, יש לנקוט בזהירות מרבית בביצוע ניסוי זה.

שוב, אין זה משנה באמת באיזה צד מבוצע ניסוי זה. עם זאת, מדידת הזרם הנקוב מרמזת כי, למטרות בטיחות, יש לבצע את הניסוי בצד המתח הגבוה. סידור הניסוי עם כל המכשירים המחוברים בצד המתח הגבוה עם קצר בצד המתח הנמוך מוצג באיור הבא:

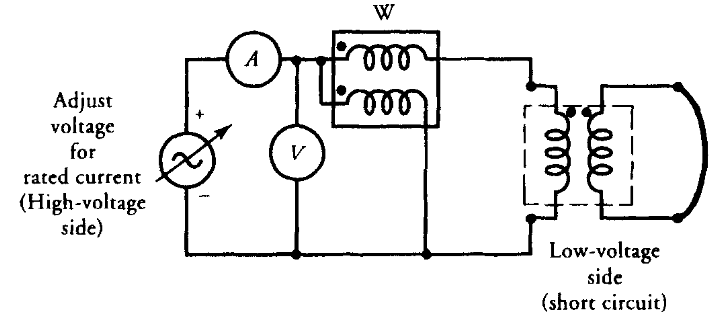
שנאי דו-ליפופי מחובר לניסוי קצר. (Guru, 2001).

מאחר שהמתח המופעל הוא שבריר קטן מהמתח הנקוב, הן הפסדי הליבה והן זרמי המגנוט כה קטנים עד שניתן להזניחם. במילים אחרות, הפסד הליבה הוא אפס למעשה והריאקטנס המגנטי הוא כמעט אינסופי. המעגל השקול המקורב של השנאי כפי שנראה מצד המתח הגבוה ניתן באיור הבא:

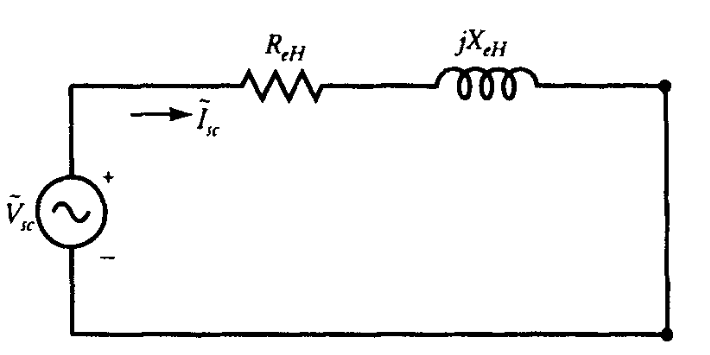
מעגל שקול מקורב של שנאי דו-ליפופי בתנאי קצר. (Guru, 2001).

במקרה זה, מד ההספק רושם את הפסדי הנחושת בעומס מלא. אם , ו- הם הקריאות במד המתח, מד הזרם ומד ההספק, אז:

הוא ההתנגדות הכוללת של שני הליפופים כפי שהיא מיוחסת לצד המתח הגבוה. גודל האימפדנס כפי שהוא מיוחס לצד המתח הגבוה הוא:

לכן, ריאקטנס הזליגה הכולל של שני הליפופים כפי שהוא מיוחס לצד המתח הגבוה הוא:

אם נגדיר את יחס ההשנאה כיחס בין מתח הצד הגבוה למתח הצד הנמוך , אז:

וכן

כאשר היא התנגדות ליפוף המתח הגבוה, היא התנגדות ליפוף המתח הנמוך, הוא ריאקטנס הזליגה של ליפוף המתח הגבוה, ו- הוא ריאקטנס הזליגה של ליפוף המתח הנמוך. אם השנאי זמין, אנו יכולים למדוד את ו- ולאמת את משוואה (GU4.31). עם זאת, אין דרך פשוטה להפריד בין שני ריאקטנסי הזליגה. הדבר נכון גם לגבי התנגדויות הליפופים אם השנאי אינו זמין. אם עלינו להפריד את ההתנגדויות, נניח שהשנאי תוכנן כך שהפסד ההספק בצד המתח הגבוה שווה להפסד ההספק בצד המתח הנמוך. זה נקרא קריטריון התכנון האופטימלי (optimum design criterion) ותחת קריטריון זה:

מה שמניב:

באופן דומה, אנו יכולים להניח כי:

קריטריון נצילות מרבית

כפי שהוגדר קודם לכן, נצילות היא היחס בין הספק המוצא להספק המבוא. בשנאי ממשי, הנצילות תמיד קטנה מ- בשל שני סוגי הפסדים עיקריים: הפסדים מגנטיים (הפסדי ליבה) והפסדי נחושת.

ההפסדים המגנטיים, המכונים לרוב הפסדי ליבה (), כוללים הפסדי זרמי מערבולת והפסדי היסטרזיס. עבור צפיפות שטף נתונה ותדר עבודה נתון, ניתן להקטין את הפסדי זרמי המערבולת על ידי שימוש בלמינציות (שכבות פח דקות) דקות יותר. הפסדי ההיסטרזיס, לעומת זאת, תלויים בתכונות המגנטיות של סוג הפלדה המשמשת לליבה. מאחר שהשטף בליבת השנאי נשאר קבוע כמעט בכל תנאי העומס, הפסדי הליבה () נחשבים קבועים במהותם. מסיבה זו, הם מכונים גם הפסדים קבועים.

הפסדי הנחושת () (הידועים גם כהפסדי או הפסדים חשמליים) נובעים מההספק המתבזבז כחום בהתנגדות של סלילי הראשי והמשני. הפסדי הנחושת משתנים ביחס ריבועי לזרם () הזורם בכל סליל. לכן, ככל שהעומס על השנאי גדל, כך גדלים הפסדי הנחושת. מסיבה זו, הם מכונים גם הפסדים משתנים.

ניתן לחשב את הספק המוצא על ידי החסרת הפסדי הליבה והפסדי הנחושת מהספק המבוא. באופן דומה, ניתן לחשב את הספק המבוא על ידי הוספת הפסדי הליבה והפסדי הנחושת להספק המוצא. ניתן להמחיש את זרימת ההספק מהמבוא למוצא באמצעות תרשים חד-קווי הנקרא תרשים זרימת הספק. תרשים זרימת הספק של שנאי מוצג להלן באיור הבא:

תרשים זרימת הספק של שנאי. (Guru, 2001).

נצילות השנאי היא אפס כאשר אין עליו עומס. ככל שהעומס גדל, הנצילות עולה עד שהיא מגיעה לערך מרבי. גידול נוסף בעומס מעבר לנקודה זו יגרום לירידה בנצילות. לכן, קיים ערך עומס מסוים שבו נצילות השנאי היא מרבית.

כעת נפתח את הקריטריון לנצילות מרבית. נתבונן במעגל השקול המקורב של שנאי, כפי שהוא נראה מהצד הראשי. זרם העומס השקול בצד הראשי (כלומר, הזרם בראשי המייצג את זרם העומס במשני) יסומן כ- ( עבור primary), ומתח העומס המיוחס לראשי הוא ו- . הספק המוצא ניתן על ידי:

כאשר הוא מקדם ההספק של העומס.
הפסדי הנחושת הכוללים, המיוחסים לראשי, הם , כאשר היא ההתנגדות השקולה הכוללת של השנאי המיוחסת לראשי ().
אם הפסדי הליבה הם , הספק המבוא הוא:

לפיכך, נצילות השנאי () היא:

במשוואה זו, עבור מקדם הספק נתון, המשתנה היחיד התלוי בעומס הוא הזרם . כדי למצוא את התנאי לנצילות מרבית, נגזור את לפי ונשווה את הנגזרת לאפס. פעולה זו מובילה לקריטריון הבא:

כאשר הוא זרם העומס השקול בצד הראשי שבו מתקבלת הנצילות המרבית.
משוואה (GU4.23a) קובעת כי נצילות השנאי היא מרבית כאשר הפסדי הנחושת שווים להפסדי הליבה. במילים אחרות, שנאי פועל בנצילותו המרבית כאשר עקומת הפסדי הנחושת (המשתנים) חוצה את עקומת הפסדי הליבה (הקבועים), כפי שמתואר באיור הבא:

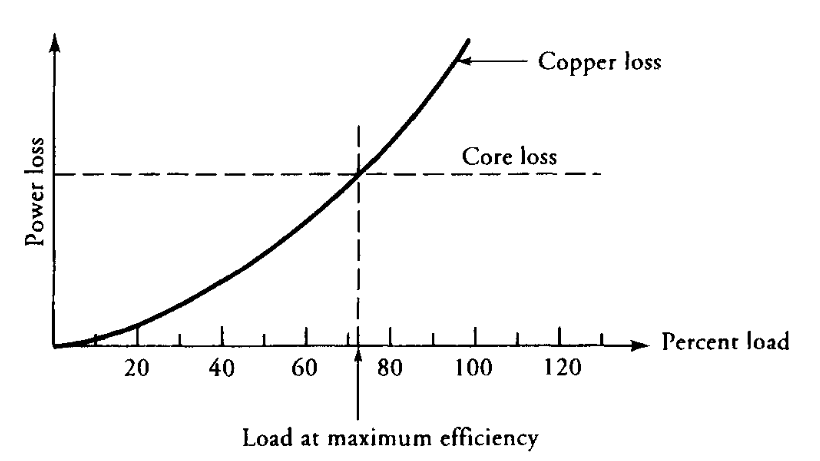
עקומות הפסדים בשנאי כפונקציה של העומס. (Guru, 2001).

ממשוואה (GU4.23a) ניתן לבטא את הזרם לנצילות מרבית:

אם הוא זרם העומס המלא (הנקוב) בצד הראשי, ניתן לבטא את משוואה (GU4.23b) גם כך:

כאשר הוא הפסד הנחושת בעומס מלא. משוואה זו מראה כי יחס הזרם בנצילות מרבית לזרם בעומס מלא תלוי ביחס בין הפסדי הליבה להפסדי הנחושת בעומס מלא.

על ידי הכפלת שני אגפי משוואה (GU4.24) במתח הנקוב בצד הראשי (), ניתן לקבל את ההספק הנדמה של השנאי שבו מתקבלת הנצילות המרבית במונחים של ההספק הנראה הנומינלי שלו:

את דירוג הוולט-אמפר לנצילות מרבית ניתן לקבוע בפועל על ידי ביצוע ניסויי מעגל פתוח וקצר בשנאי.

→ קודם: ELM1_005הבא: ELM1_007 ←