FEM1_002 אלסטוסטטיקה חד-ממדית

בעיית מידול: אלסטוסטטיקה חד-ממדית

מבוא: בעיית מידול

ברוב הבעיות הפיזיקלית הפתרונות האמיתיים לא חלקים; כלומר, הם לא גזירים ברציפות. נביט למשל במשוואה של שיווי משקל סטטי מכנית:

כאשר הוא טנזור המאמץ ו- הוא כוחות הגוף.
כדי לפתור את משוואה זו בשיטות נומריות שאנו מכירים, אנו צריכים שהמאמץ, , יהיה גזיר. למעשה משוואות מתמטיות מהצורה של קיימות גם בבעיות פיזיקליות אחרות כמו דיפוזיה, הולכת חום, זרימה וכו’. ברוב המקרים, גזירות היא דרישה מחמירה מדי, והיא לא מתקיימת - הפתרון “יקפוץ”. לכן, כאשר אנו פותרים בעיות מסוג זה אנו “נחליש” את הדרישות. שיטות נומריות שמשתמשות בצורות חלשות, כמו שיטת אלמנטים סופיים, פותחו מהתכונה הבסיסית שכאשר פתרון קלאסי חלק קיים, הוא גם פתרון של ההבעית בצורה החלשה. לכן, אנו לא מאבדים מידע כאשר אנו עוברים מהבעיה המקורית לצורתה החלשה.

נתחיל מבעיות חד-ממדיות פשוטות התופסות את המרחב הפתוח , עם השפה . השפה כוללת עקומה עליה מוגדרים ההזזות (או כל משתנה אחר אותו אנו רוצים לחקור, כמו טמפרטורה או ריכוזיות), ועקומה עליה מוגדרים הטרחות (וקטורי הטרחה ). במילים אחרות, במקרה הכי כללי, התנאי שפה יהיו מסוג דיריכלה או נוימן.

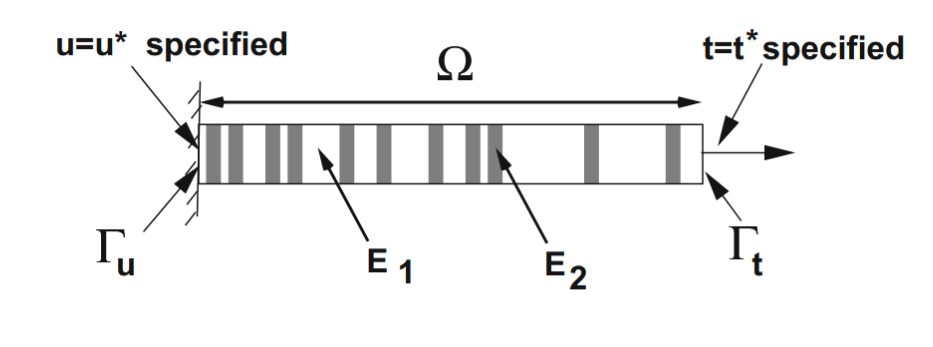
גוף חד ממדי. (Zohdi, 2018).

נתחיל מפיתוח הצורה החלשה של צורתה החד-ממדית של משוואה :

כאשר (מודול יאנג) משתנה במרחב.

צורה חלשה

כדי לפתח את הצורה החלשה של משוואה מסוימת, למשל של , שנקראת הצורה החזקה, נכפיל אותה בפונקציה שרירותית חלקה , ונבצע אינטגרציה לאורך הגוף:

כאשר הוא השארית. אנו קוראים ל- פונקציית מבחן (test). אם נוסיף את התנאי שאנו מבצעים זאת לכל פונקציית מבחן אפשרית אז

מה שאומר ש- . לכן, אם ניקח בחשבון כל פונקציית מבחן , אז

על כל תחום סופי ב-. לפיכך, הצורה החלשה והצורה החזקה יהיו שקולים, בהנחה והפתרון האמיתי חלק מספיק כך שיש לו פתרון חזק. ניתן לראות ש- חייב להיות אפס בכל תחום סופי בגוף, כי פונקציית המבחן “תמצא” אותו:

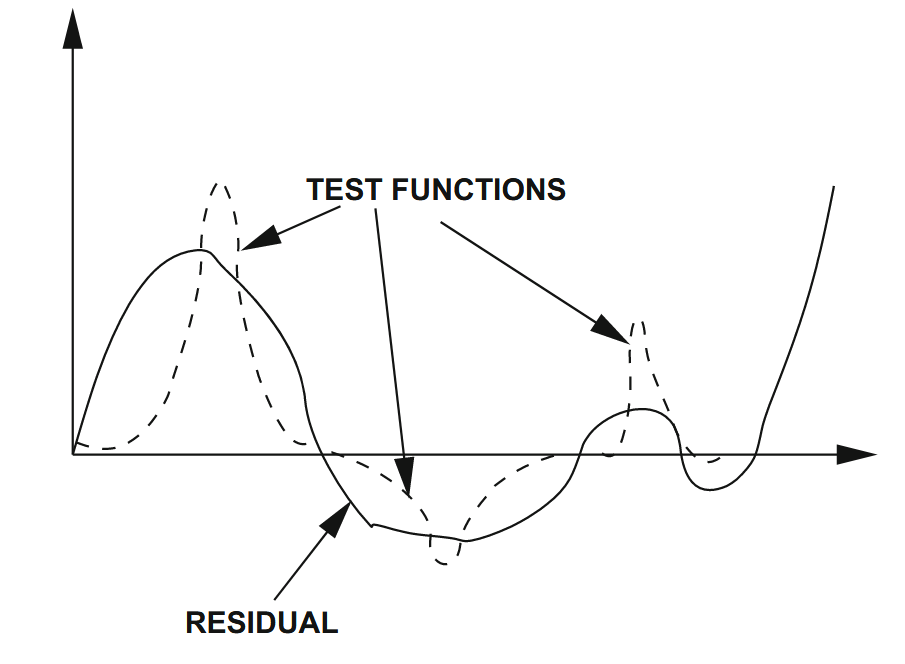
פעולת פונקציית המבחן על שאריות. (Zohdi, 2018).

לפי נגזרת של מכפלה על גזירה של , נקבל:

מה שאומר שלכל :

ולאחר העברת אגפים, לכל מתקיים:

על , המאמץ על השפה ידוע, , אבל הוא לא ידוע על . לכן, נחליט לצמצם את הבחירה של פונקציות המבחן לכאלה שמקיימות . נוכל כעת לנסח את הבעיה מחדש:

עלינו למצוא (הפתרון שלנו), כאשר (תנאי שפה כלשהו מסוג דיריכלה), כך שלכל שמקיים מתקיים

זו נקראת הבעיה בצורתה ה-חלשה כי היא לא דורשת גזירות של . במילים אחרות, דרישות הגזירות נחלשו.

דוגמה:

נגדיר פונקציה רציפה (כלומר, רציף בתחום ) על תחום חד ממדי . אנו טוענים כי אם לכל , אז .
נוכל להוכיח זאת בשלילה. נניח ש- בנקודה כללית . מאחר ו- , חייב להיות תת-קטע , שנגדירו , כך של- יש את אותו הסימן כמו בנקודה . מאחר ו- שרירותי, נוכל לבחור שערכו אפס מחוץ לקטע זה, ועם אותו הסימן של בתוך הקטע.

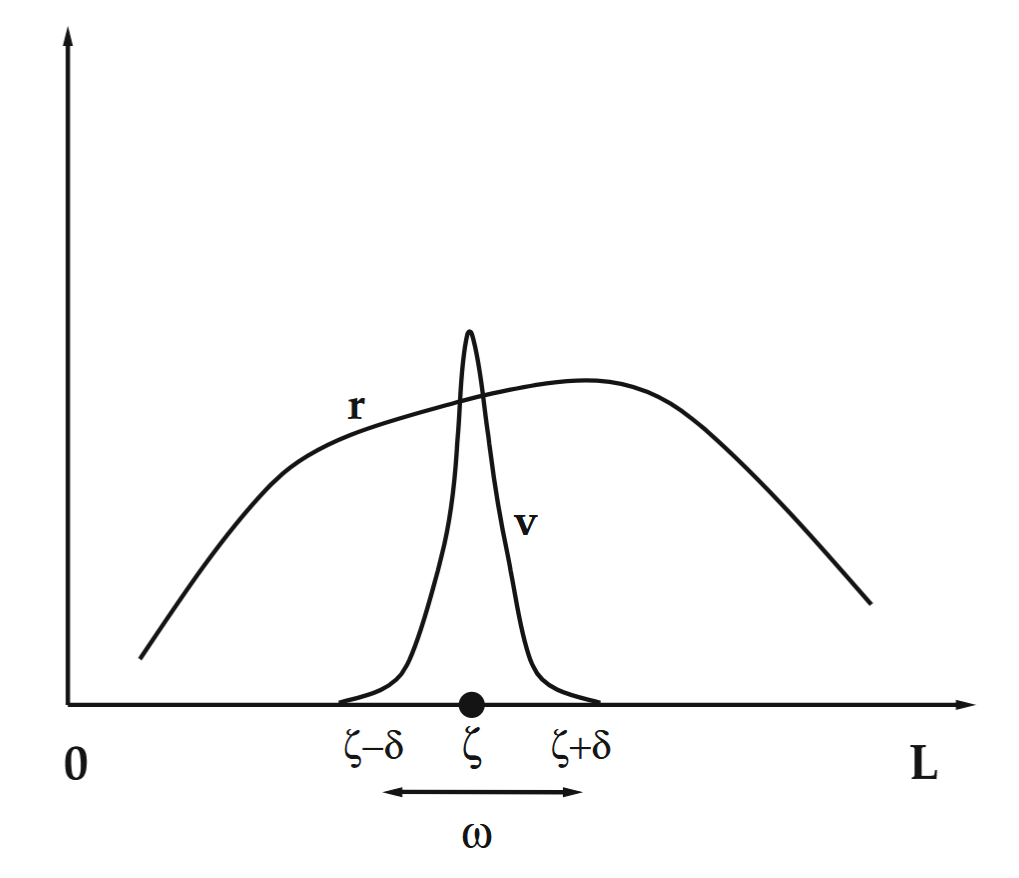
פונקציית שארית ופונקציית מבחן.

זה אומר ש:

שזו סתירה.
כעת נבחר

מה שאומר ש:

ולכן (כלומר, גזירה ברציפות פעמיים ב-). לכן, לבעיה זו, הצורה החזקה והצורה החלשה שלה שקולות אם - כלומר, אם הפתרון גזיר ברציפות פעמיים.

מרחב סובולב הילברטני

בעיה מרכזית היא בחירת הפונקציות בצורה החלשה. בתמימות, נוכל לומר שהתשובה היא פשוטה - האינטגרלים חייבים להישאר סופיים. כלומר, האילוצים הם שלכל :

כדי לנסח ביטויים יותר מפורשים, עלינו לפנות למערכת הנקראת מרחבי סובולב הילברטניים (Hilbertian Sobolev spaces). מסתבר יש משהו כזה שנקרא מרחב הילברט, ויש משהו שנקרא מרחב סובולב, ופה לוקחים שילוב של שניהם או משהו כזה.
ניזכר בשלושת התנאים בהגדרה של נורמה נורמה (ממש תלכו לשם ותקראו את שלושת התנאים, אין לי כוח לכתוב אותם פה). סוג מסוים של נורמות, שנקראות נורמות מרכב הילברט (Hilbert space norms), נמצאות בשימוש רב בפיזיקה. כמוסכמה, אנו מסמנים ב- את המרחב של פונקציות סקלריות עם נגזרות חלקיות מסדר ב-. כלומר, היא אינטגרבילית בריבוע. במילים אחרות, אם:

בעזרת הגדרות אלו, נוכל לנסח בעיית תנאי שפה באופן מלא. אנו מניחים שכוחות הגוף והמאמצי הטרחה בשפה , אבל ניתן גם לפתור עם נתונים פחות חלקים בלי עלייה משמעותית בסיבוכיות. ניסוח הבעיה:

עלינו למצוא (הפתרון שלנו), כאשר (תנאי שפה כלשהו מסוג דיריכלה), כך שלכל שמקיים וגם , מתקיים

נשים לב שאם המידע (הנתונים) ב- חלק, אז הוא הפתרון לבעיה הקלאסית בצורתה החזקה