FEM1_004 דיוק שיטת אלמנטים סופיים בחד-ממד

מבוא

כפי שראינו, הרעיון המרכזי בשיטת האלמנטים הסופיים הוא לבחור קירוב סופי של הפתרון האמיתי ולנסח את הבעיה החלשה הבאה:

מציאת , עם , כך ש-

כאשר , עם .

אנו מתייחסים ל- ו- כמרחבי הקירוב (למשל, פונקציות לינאריות). הנקודה הקריטית היא ש-. קירוב “פנימי” זה מאפשר פיתוח של אומדני שגיאה פשוטים. אנו נבחר ב- ו- כזהים.

הגדרה:

לכל פונקציה קבילה , נגדיר את סמי-נורמת האנרגיה (energy semi-norm) כך:

אם תנאי השפה אינם מאפשרים תנועה קשיחה (כלומר, אפשרי רק אם ), אז סמי-נורמת האנרגיה הופכת לנורמה מתמטית קלאסית רגילה.

אומדן שגיאה בשיטת האלמנטים הסופיים:
תחת הנחות די מתונות, ניתן להראות ש:

כאשר הוא סדר הפולינום של פונקציות הבסיס, הוא רמת החלקות של הפתרון האמיתי, הוא גודל האלמנט המקסימלי, ו- הוא קבוע התלוי בפתרון ובפולינום אך לא ב-. לא ניכנס לפיתוח של ביטוי זה.

הערה:

נציין כי קבוצת הפונקציות המוגדרות ע”י עם אינה טכנית מרחב של פונקציות ויש לאפיין אותה כ”מגוון לינארי”. הדבר אינו מהווה בעיה לניתוח שיבוא.

הערה:

נציין כי היא נורמה מכיוון ש:

• היא חיוביות: כאשר, בהינתן ש-, אם ורק אם .
  • מתקיים אי-שוויון המשולש:
  • ניתנת להכפלה בקבוע:

משפט “הקירוב הטוב ביותר”

פתרון שיטת האלמנטים הסופיים הוא האופטימלי ביותר מבחינת נורמת האנרגיה. כדי להוכיח זאת אנו משתמשים במשוואה :

לכל עם (הפתרון המדויק), ו-

לכל עם (הפתרון הנומרי).

חיסור משוואה מ- (כאשר מציבים במשוואה הראשונה) מוביל לתכונת אורתוגונליות בסגנון גלרקין:

לכל עם , כאשר השגיאה מוגדרת כ- .

נבחר כעת כלשהו ונגדיר . אז:

כאשר הוא קירוב קביל קינמטית של הפתרון האמיתי. באמצעות ייצוג זה והתכונה מ-, אנו מקבלים:

מכיוון ש-, נקבל:

זהו משפט הקירוב הטוב ביותר, המראה שהקירוב המתקבל משיטת האלמנטים הסופיים הוא הטוב ביותר מבין כל הקירובים האפשריים במרחב מבחינת נורמת האנרגיה.

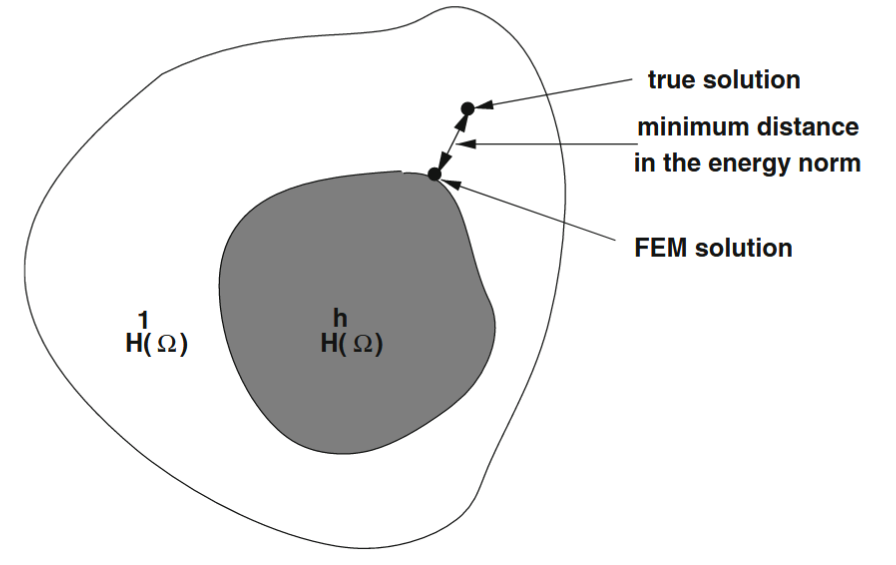
סכמה של משפט הקירוב הטוב ביותר. (Zohdi, 2018).

עקרון האנרגיה הפוטנציאלית המינימלית

עקרונות מינימום הם קבוצה של מושגים מועילים ביותר בפיזיקה. נראה כעת כיצד הם מתקשרים לשיטת האלמנטים הסופיים.

יהי פונקציה קינמטית קבילה כלשהי (כלומר, פונקציה המקיימת את תנאי הגבול). באמצעות הגדרת נורמת האנרגיה, נקבל:

נארגן מחדש את הביטוי:

מכיוון שהפתרון האמיתי מקיים את משוואת הבעיה החלשה לכל עם , וגם מקיים את תנאי הגבול ההומוגני (שכן ו- מקיימים את אותם תנאי גבול), נוכל להציב ולקבל:

כאשר הגדרנו את ה”פוטנציאל” באופן הבא:

מכיוון ש- עבור כל , נקבל:

ביטוי זה ידוע כעקרון האנרגיה הפוטנציאלית המינימלית (Principle of Minimum Potential Energy - PMPE). במילים אחרות, הפתרון האמיתי ממזער את האנרגיה הפוטנציאלית מבין כל הפונקציות הקבילות מבחינה קינמטית.

אומדנים פשוטים לרשתות FEM מתאימות

התוצאות שהצגנו בסעיפים הקודמים מאפשרות לנו לפתח אומדנים לגודל הרשת הנדרש כדי להשיג דיוק מסוים.

כפי שראינו במשוואה , תחת הנחות סבירות, שגיאת הקירוב של שיטת האלמנטים הסופיים מוגבלת על ידי:

כאשר:

• הוא סדר הפולינום של פונקציות הבסיס (למשל, עבור פונקציות לינאריות)
• הוא מדד החלקות של הפתרון האמיתי (בד”כ מוגדר לפי מרחב סובולב )
• הוא הגודל המקסימלי של אלמנט ברשת
• הוא קבוע שאינו תלוי ב- אלא רק בפתרון ובסדר הקירוב

בנוסף, משילוב עם עקרון האנרגיה הפוטנציאלית המינימלית (משוואה ) עבור , נקבל:

משוואה זו מספקת קשר ישיר בין שגיאת האנרגיה לבין הפרש האנרגיה הפוטנציאלית בין הפתרון המקורב לפתרון האמיתי.

חישוב קבוע השגיאה והערכת גודל הרשת

מכיוון שהפתרון האמיתי אינו ידוע לנו בדרך כלל, איננו יכולים לחשב ישירות את . במקום זאת, אנו יכולים לפתור את הבעיה עם שתי רשתות בעלות רזולוציות שונות, , ולהעריך את קבוע השגיאה .

בהינתן ש- (הנובע מעקרון האנרגיה המינימלית), נוכל להציב במשוואת השגיאה:

על ידי חיסור המשוואות זו מזו ופתרון עבור , נקבל:

לאחר שמצאנו את , אנו יכולים לחשב את גודל הרשת הנדרש כדי להשיג שגיאה קטנה מסף נתון :

לסיכום, תהליך הערכת גודל הרשת האופטימלי מורכב מהצעדים הבאים:

אלגוריתם: חישוב גודל רשת אופטימלי

1. פתרון על רשת גסה:
   פתור את הבעיה על רשת עם גודל אלמנט וחשב את ערך האנרגיה הפוטנציאלית .

2. פתרון על רשת עדינה יותר:
   פתור את אותה בעיה על רשת עדינה יותר עם גודל אלמנט (כאשר , למשל ) וחשב את .

3. חישוב קבוע השגיאה והערכת גודל הרשת האופטימלי:
   חשב את קבוע השגיאה באמצעות משוואה ואז קבע את גודל הרשת האופטימלי לפי משוואה .

הערות:

• לרוב בוחרים , כלומר מחצית את גודל האלמנט בין הרשת הגסה לעדינה.
• שיטה זו מספקת הערכה גלובלית לגודל הרשת, אך באזורים מורכבים של הפתרון (למשל, שינויים חדים) ייתכן שנדרש עידון רשת מקומי נוסף.
• בפועל, כדאי להשתמש בערך שמרני יותר של מזה שחושב, כדי להבטיח שהשגיאה אכן תהיה קטנה מהסף הנדרש.

רשת שעודנה ב- כדי להעריך את השגיאה. (Zohdi, 2018).

עידון רשת מקומית (Local Mesh Refinement)

בעוד שהשיטות הגלובליות שתוארו לעיל מאפשרות לנו להעריך את גודל הרשת הממוצע הדרוש, לעתים קרובות אנו זקוקים לרשת צפופה יותר באזורים מסוימים של התחום, במיוחד היכן שהפתרון משתנה במהירות (למשל, ליד גבולות או מקורות).

שיטות מבוססות שארית

הגישה הפשוטה והיעילה ביותר לעידון רשת מקומי היא להשתמש בשארית (residual) כמדריך לאזורים שבהם דרוש עידון. יתרונה של גישה זו הוא שהיא אינה דורשת פתרון של מערכת משוואות נוספת, אלא רק חישוב של מספר ביטויים מקומיים.

שיטות מבוססות שארית משתמשות בשלושה מקורות מידע:

1. פתרון שיטת האלמנטים הסופיים עצמו ()
2. תנאי הגבול הנתונים
3. משוואת השגיאה ותכונת האורתוגונליות של גלרקין

באמצעות אלה, ניתן לבנות את החסם השגיאה הבא:

כאשר:

• , ו- הם קבועים
• הוא גודל האלמנט
• היא השארית הפנימית של האלמנט, המוגדרת כ:

שארית זו מודדת עד כמה הפתרון המקורב מפר את המשוואה הדיפרנציאלית בתוך האלמנט.

• היא ה”קפיצה” בשטף בממשק בין אלמנטים, המוגדרת כ:

כאן ו- מייצגים את הצדדים הימני והשמאלי של הממשק, בהתאמה. הקפיצה בשטף מודדת את אי-הרציפות של הנגזרת הראשונה (המוכפלת ב-) בגבולות בין אלמנטים.

• היא שארית גבול חיצוני, המוגדרת כ:

שארית זו מודדת את מידת אי-קיום תנאי הגבול מסוג נוימן.

אינדיקטורי שגיאה מקומיים

בהתבסס על החסם לעיל, אנו יכולים להגדיר אינדיקטור שגיאה מקומי לכל אלמנט:

אינדיקטור זה מורכב משלושה מרכיבים:

1. שארית הפנימית (חוסר קיום המשוואה הדיפרנציאלית בתוך האלמנט)
2. קפיצות בשטף בממשקים בין אלמנטים
3. חוסר התאמה לתנאי גבול מסוג נוימן

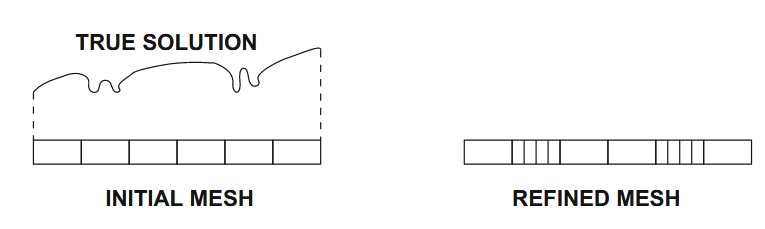
רשת מעודנת מקומית לחישוב פתרונות מקומיים מדויקים יותר. (Zohdi, 2018).

אלגוריתם עידון מקומי

האלגוריתם הפשוט ביותר לעידון רשת מקומית מבוסס על הצעדים הבאים:

1. פתרון הבעיה: פתור את בעיית האלמנטים הסופיים על הרשת הנוכחית.
2. חישוב אינדיקטורי שגיאה: חשב את ערך לכל אלמנט ברשת.
3. בחירת אלמנטים לעידון: כל אלמנט שעבורו מסומן לעידון.
4. עידון הרשת: חלק את האלמנטים המסומנים לאלמנטים קטנים יותר.
5. חזרה: חזור לצעד 1 עד שכל האינדיקטורים קטנים מהסף הנדרש .

שיטה זו מאפשרת לנו ליצור רשת מותאמת באופן אופטימלי לבעיה הספציפית, עם אלמנטים קטנים יותר באזורים שבהם הפתרון משתנה במהירות ואלמנטים גדולים יותר באזורים שבהם הפתרון חלק יותר. זהו יתרון משמעותי של שיטת האלמנטים הסופיים האדפטיבית על פני שיטות עם רשת אחידה.